多重網格法在直流電法中的正演研究
蔣亮++郭軒++王鵬瑞

摘要:自從多重網格法于20世紀60年代提出后,經過40多年的研究和發展,有了完整的理論體系,算法趨于成熟,被認為是當今數值計算領域高效算法之一。以其收斂速度快,計算精度高等優點在勘探地球物理領域得到一定應用。本文從多重網格法的基本思想出發,介紹了多重網格法的基本思想及理論公式。并將多重網格法應用到溫納裝置測量的正演響應中,應用多重網格法進行正演模擬的溫納裝置,可以直觀準確的反應出模型的異常區的大小和方向。能夠給直流電法的正演研究提供一定的準確性。
關鍵詞:多重網格;溫納;限制算子;插值算子
1.多重網格法的發展現狀
多重網格法簡稱MG,是數學家Fedorrenko于20世紀60年代最早提出的,直到Brandt關于“邊值問題多重網格適應解”的文章發表后,多重網格法才開始得到廣泛的關注和全面研究[1]。多重網格法是目前近乎最優的算法之一,有其固有的特點:收斂速度跟網格的大小無關,而且這一特性同樣適應于求解復雜問題。多重網格法經過近30年的研究和發展,有了完整的理論體系,算法趨于成熟,在流體力學,計算電磁學,波動方程等領域都有所應用,是當今數值計算領域常用的算法之一。近二十年也逐漸的應用于地球物理領域中。
2.多重網格法的基本思想及理論公式
多重網格法其主要思想是在不同的網格層中,可以使不同頻率的誤差分量因網格間距的不同逐漸被衰減掉[2]。首先把以當前網格為基礎的低頻分量限制到比較粗的網格上,這樣就會使原本看起來比較光滑的的低頻分量在粗網格上又重新跳動振蕩起來,然后根據松弛迭代的方法對其進行處理,這樣會使在粗網格上誤差又變得光滑起來,繼續將其限制到更粗的網格上進行光滑迭代,重復以上過程直至最粗限度的網格。到最粗的網格結束后將其每層網格迭代光滑后的誤差經線性插值后再逐級返回至細一層網格,將這些返回后的誤差對方程解進行校正,就可以得到更為精確的解,至此一次多重網格的循環結束[3]。
以2層網格為例進行理論推導:
假設存在一個均勻剖分的兩重網格如圖,細網格的步長是h,粗網格的步長是H,H=2h,用線性方程表示剖分最細的網格層:
圖1 二維模型均勻剖分圖
Ahuh=fh(1)
Ah是系數矩陣,fh是右端項,uh是方程的精確解。
在細網格層上進行1次松弛迭代,uh1是迭代過后的近似解,uh1和uh間高頻分量因迭代而衰減。
uh-uh1=eh1是誤差向量,rh1就是殘差向量
Ah(uh-uh1)=Aheh1=fh-Ahuh1=rh1(2)
將(2)式近似到粗網格上,AHeH=rH1(3)
由細到粗需要加入限制算子RHh(線性算子),使rH1=RHhrh1(4)
求解(3)得到eH1,加入插值算子PhH(線性算子),
得到eh1的近似解e1h,則e1h=PhHeH1(5)
可以方便的計算出公式(4)和(5)。最后就可以得出修正后的近似解h1
h1=uh1+e1h(6)
這是2層V循環的理論公式,亦可以看成任意相鄰網格層間的轉換公式。
在上述求解過程中,限制和插值算子是其重要組成,常用的是線性插值及完全加權限制,因是均勻剖分,故其常用的9點限制算子和插值算子分別是:
RHh=1161811618141811618116,PhH=121242121(7)
3.MG法三維響應模擬
將多重網格法應用于以有限差分為基礎的高密度正演中,以溫納裝置對典型的地下異常體進行測量,電流都是I=1A,電極距為5米,測線總長度100米,則測區范圍一共有21個電極。網格剖分為49×49×31,剖分模式為不等距剖分,中間細網格,邊界剖分為指數增長的網格。構建三維模型
3.1不同測線方向的異常響應
圖2 不同測線分布圖
為了突顯正演的響應,在用溫納測量時,從不同的傾角進行測量,如圖2θ是測線與X軸的夾角,(θ0=0;θ1=30;θ2=45;θ3=60;θ4=90),在用溫納裝置測量時,會得到63個測點數據,測得地下深度42.5米;在用偶極-偶極測量時,會得到171個測點數據,測得地下深度47.5米。以低阻異常為例,異常體的電阻率為1Ω·m,圍巖電阻率為100Ω·m,異常體埋深為Z方向3到10米,X方向為-10米到10米。
當地下異常體是一個沿Y方向延伸的二度體,通過溫納裝置從不同角度的到的視電阻率圖(圖3)。
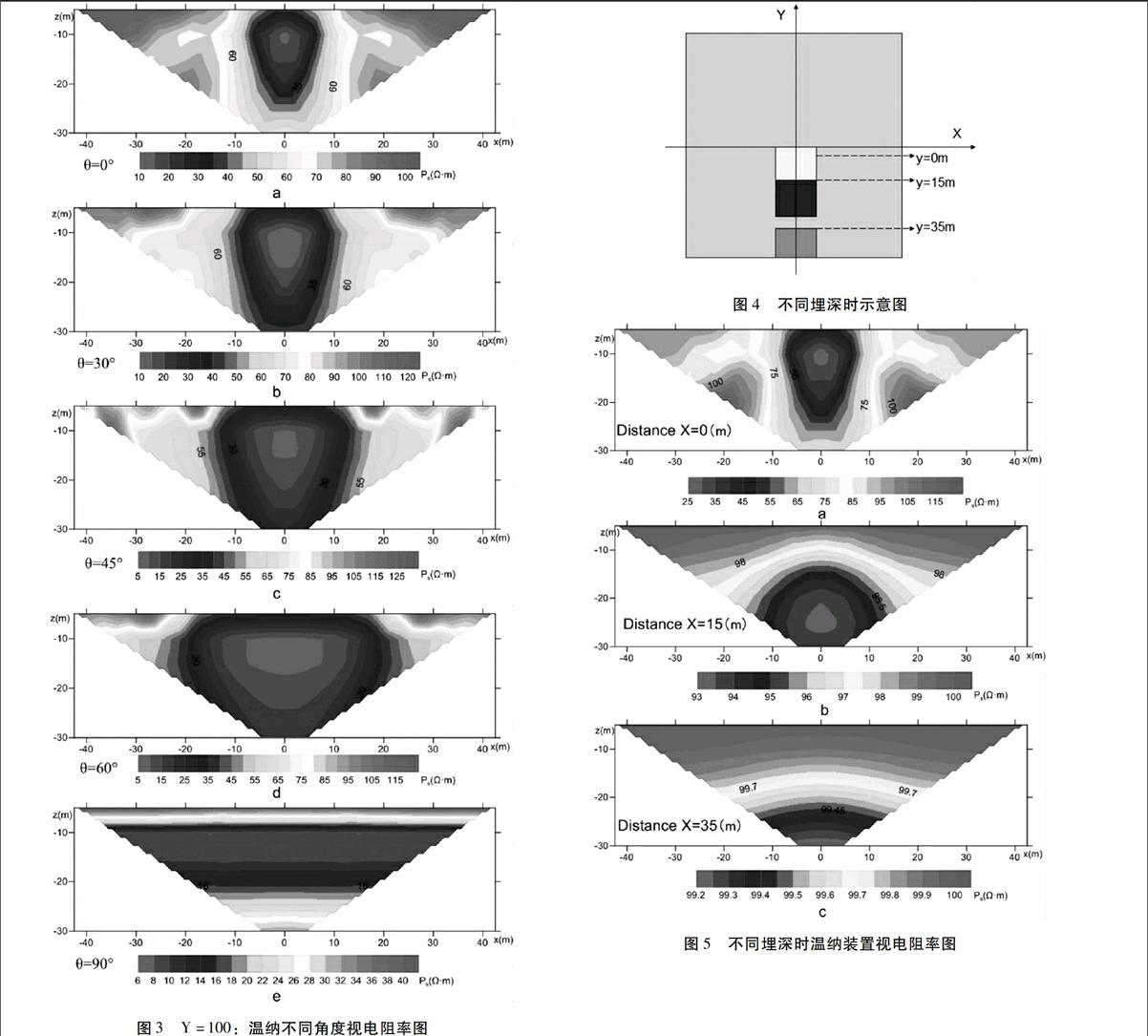
圖3 Y=100:溫納不同角度視電阻率圖
利用溫納裝置測量時,當θ0=0°時測線垂直橫穿過低阻異常體,此時可以得到一個范圍比較小可近似看成倒梯形的低阻異常范圍,實際范圍X方向比較準確在模型范圍內,Z方向向下延伸比較多;當θ0=30°、45°、60°時同樣可以得到異常區域范圍X方向逐漸變大,直至90°時通過圖e可以看到,視電阻率圖所呈現的是一個地下均勻平行的兩層介質。
3.2異常體埋深的響應
前面得到了測線穿過異常體的各種情況,本節將研究當模型參數不變時,測線不穿過異常體,并與異常體垂直距離不等時的響應特征。溫納的裝置參數都不變,當異常體垂直距離測線Y=0、15、35米時如圖4。
經過兩種裝置測量后,得到圖5,如圖所示,隨著與測線垂直距離的不斷加大,正演響應均有一定變化。當Y=0m時,相當于垂直橫穿過異常體,與5.1中θ=0時情況相同;當Y=15m時,異常區域均有向下的趨勢,但是X方向范圍變化不大;當Y=90m時,異常區域都為位于圖片的下方,幾乎脫離視電阻率圖。總結來說,當異常體與側向越近時,響應特征越好,隨著距離的增加,異常響應會逐漸向下,最后移出測量范圍。
圖4 不同埋深時示意圖
圖5 不同埋深時溫納裝置視電阻率圖
結論
在應用多重網格法進行迭代計算的基礎上,用溫納裝置對地下典型的異常體模型進行正演模擬,通過對正演響應的分析發現,地下存在二度體和異常體Y的長度變短時的情況下,從不同角度進行測量時響應的結果差別很大,只有當測線垂直穿過異常體時,響應結果最好;當異常體與測線距離不同時,距離越近,正演響應越接近真實模型。以上兩種正演響應均能較好的反應出不同條件下的模型特征,相信多重網格法未來在物探領域應該有更好的發展。
參考文獻:
[1]Alcouffe R.E.,Brandt A.,Dendy J.E.,and Painter J.W..The multi-grid method for the diffusion equation with strongly
[2]喬中林.直流電法三維正演多重網格算法研究[D].北京:中國地質大學,2007.
[3]魯晶津.地球電磁三維數值模擬的多重網格方法及其應用研究[D].合肥:中國科學技術大學,2010.endprint

