數字預失真器模型參數辨識算法研究*

韓　冰，晉東立

(北京跟蹤與通信技術研究所，北京 100094)

?

數字預失真器模型參數辨識算法研究*

韓冰，晉東立

(北京跟蹤與通信技術研究所，北京 100094)

修回日期：2015-05-22Received date:2015-03-13；Revised date：2015-05-22

摘要：數字基帶預失真技術是補償功放非線性的最有效方法之一，而自適應算法的選擇很大程度上影響著系統的預失真性能。其中，最小均方誤差(LMS)算法和遞歸最小二乘法(RLS)是最常用的自適應收斂算法，在綜合分析兩種算法優缺點的基礎上，提出了一種基于正弦函數的歸一化LMS(NLMS)算法和RLS算法的組合算法。仿真結果表明，該組合算法在達到與RLS同樣預失真精度的前提下，可大大減小計算量。

關鍵詞：功率放大器；數字預失真；正弦函數 NLMS；RLS；變步長

0引言

功率放大器是通信系統的重要組成部分，其作用是將射頻信號的功率進行放大，以此來滿足發射機對發射功率的要求，信號經過功放產生失真，與功放的兩個性能指標：要求非線性失真小與功率效率盡可能高，是一對矛盾關系。早期，采用功率回退法以減小功放的非線性失真，但導致功放效率降低。為提高功放的效率，一般使功放工作在非線性區，帶來的影響是帶內誤碼率升高以及帶外頻譜擴展。目前，數字預失真是補償功放非線性最有效的方法之一，其原理是在功放前加一個與功放特性互逆的預失真器，優點是硬件實現簡單、適應性強以及效率高。而且數字信號處理(DSP)技術的發展將會帶動數字預失真技術更廣泛的應用。

目前，查表法和多項式法是數字預失真常用的兩種技術手段[1]。查表法的精度與存儲表項的大小直接相關，表項越多，預失真精度越高，但所需的存儲空間也越大；多項式預失真自適應能力好，可采用高階多項式來實現較高的預失真性能。預失真模型建立以后，可以采用直接學習結構和間接學習結構對系統進行辨識，其中采用間接學習結構可以省略對功放參數的辨識，復雜度較低。

傳統的經典的自適應算法是LMS算法和RLS算法[2]。RLS算法收斂性較好，但復雜度較高；傳統的固定步長的LMS算法收斂速度慢，易陷入局部最優且精度不高[3]。本文選擇記憶多項式作為預失真器的數學模型，采用RLS和變步長LMS算法相結合的自適應算法的間接學習結構對預失真系統的參數進行辨識，收斂速度得到提升，帶內失真得到改善，帶外頻譜擴展得到了有效抑制。

1預失真的自適應收斂算法

通信預失真系統如圖1，模型建立和模型辨識是預失真系統的兩個重要組成部分。

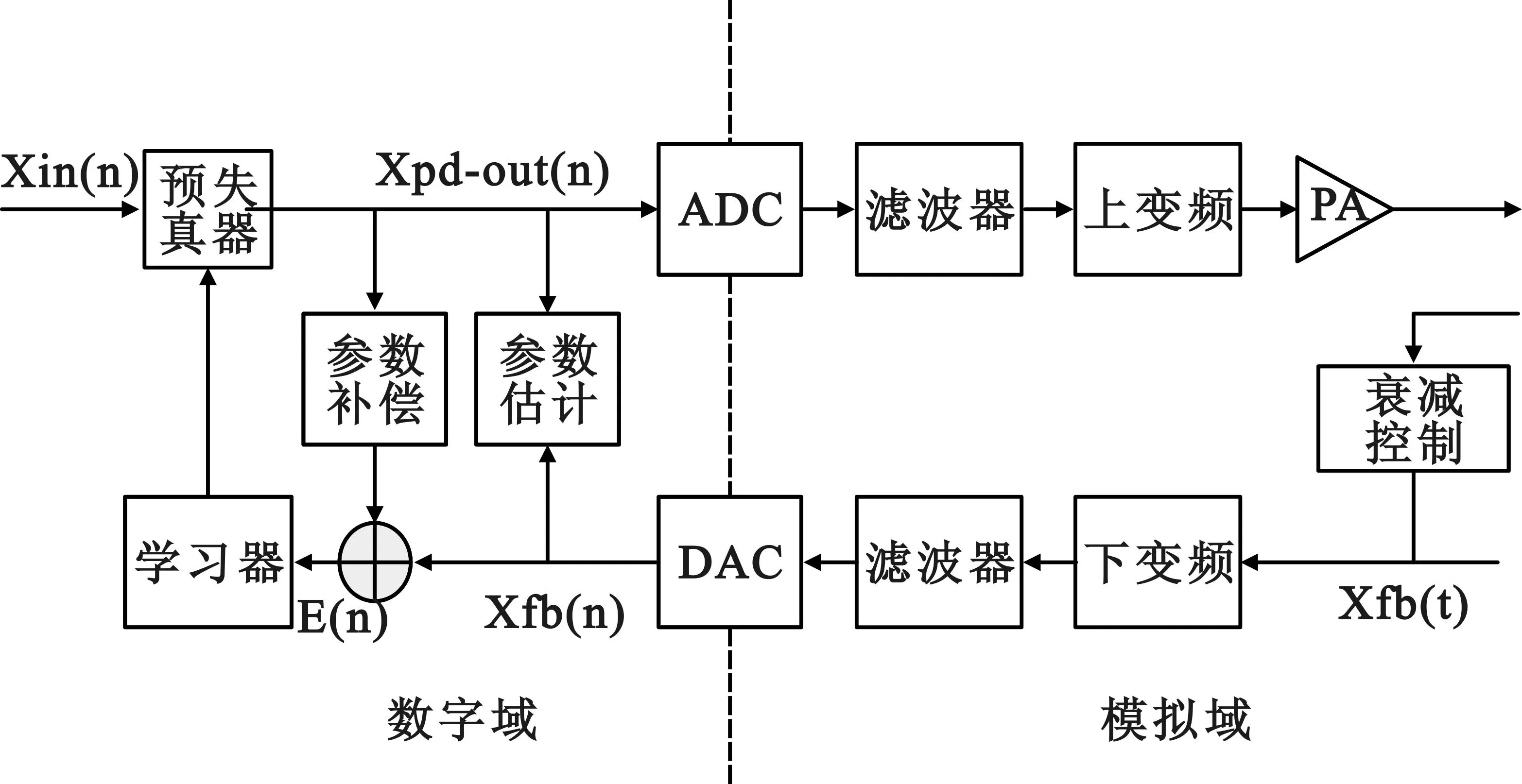
圖1　預失真系統結構圖

本文選擇Saleh模型[4]作為功放模型，以多項式模型為預失真器模型，其中，Saleh功放模型的輸出信號幅度與輸入信號幅度之間的關系為：

(1)

輸出信號相位較輸入信號相位增加為：

(2)

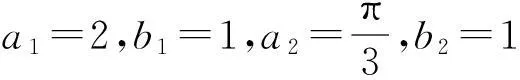
對于無記憶功放模型而言，基于多項式的預失真器模型的數學表達式為[4]：

(3)

采用間接學習結構對預失真器參數進行辨識，間接學習結構框圖如圖2所示。

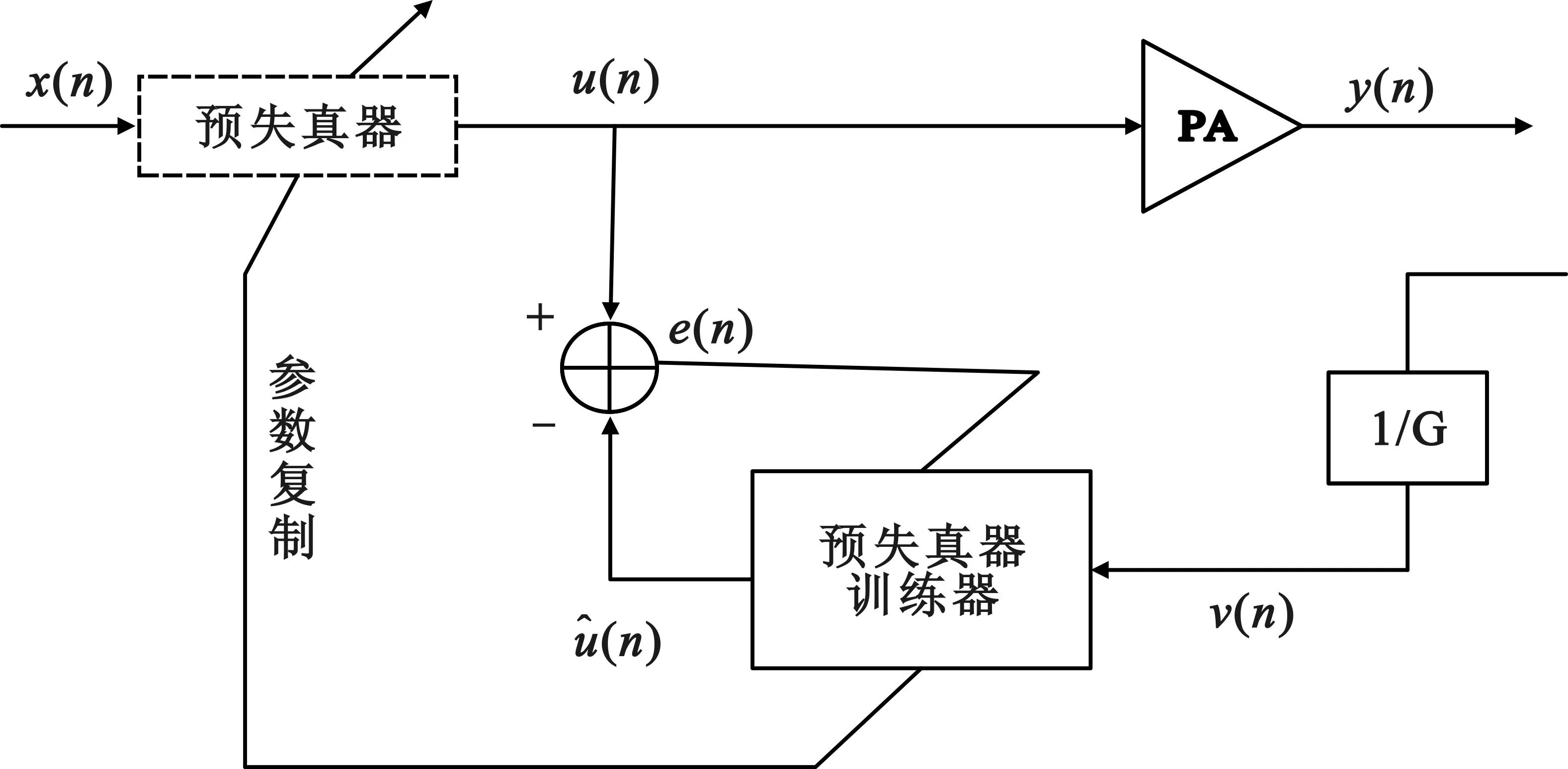
圖2間接學習結構框圖

(4)

λ為遺忘因子，一般取0<λ<1。RLS收斂速度快，收斂性能好，但是計算量大，實現較為復雜。

傳統的固定步長的LMS算法的迭代過程為：

y(n)=HPA(u(n))

(5)

(6)

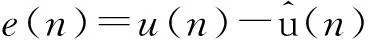
(7)

W(n+1)=W(n)+μe*(n)u(n)

(8)

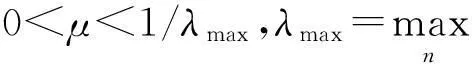
針對LMS算法的研究幾種在變步長LMS算法上，變步長算法遵循的一般原則為，當初始階段誤差較大時，步長因子應較大，以加速收斂，當誤差較小時，選擇較小的補償因子，保證收斂的穩態。能同時獲得較小的穩態誤差和較快的收斂速度，基于Sigmiod函數的變步長LMS算法(SVSLMS)的步長因子為：

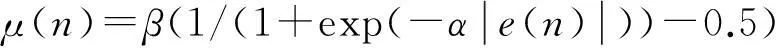
(9)

不過此算法在誤差e(n)接近0時變化較大，使得SVSLMS算法在自適應穩態階段仍有較大的步長變化。為解決這個問題，文獻[5]在SVSLMS算法的基礎上提出的變步長算法(G-SVSLMS)為：

(10)

此時，μ(n)在e(n)接近0時，變化緩慢，收斂速度較快，但是此算法僅與當前時刻的誤碼有關，抗噪能力較差，當信噪比較低時，算法精度容易受到影響。

由于噪聲的存在，G-SVSLMS算法不能較好反映自適應狀態的迭代過程，于是文獻[6]提出如式(11)的改進算法：

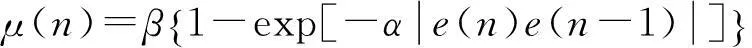
(11)

上述LMS類算法的步長因子均與反饋誤差有關，還有一類與輸入信號有關的變步長LMS算法，歸一化LMS(NLMS)算法[7]就屬于這類變步長算法，其步長因子表達式為：

(12)

文獻[8]提出了一種基于正弦波的LMS算法，其變步長因子的數學表達式為：

(13)

其中,β控制步長因子的取值范圍，直接影響算法的收斂速度，α主要控制誤差接近零時的穩態。增大β可以加快算法的收斂，但是為避免發散，β不宜取值過大。

文獻[9]把當前時刻信號的功率考慮在內，即把歸一化LMS算法和基于正弦函數的LMS算法結合起來，形成一個新算法——基于正弦函數的歸一化變步長LMS算法，這里把它簡寫為S-NLMS算法。其數學表達式為：

(14)

綜合考慮上述自適應算法的特點以及本文所選擇的功放模型和預失真器模型，提出一種新的自適應算法，即RLS算法和基于正弦函數的NLMS算法相結合的應用，初始階段，選擇收斂速度較快的RLS算法，當收斂趨于穩定后，改用NMLS算法，算法原理圖如圖3所示，當迭代次數n=N1時，選用NMLS算法。

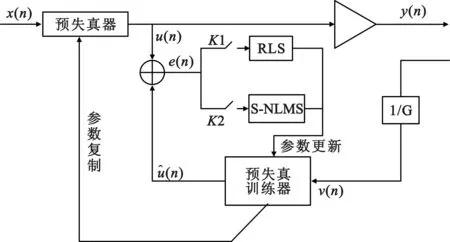
圖3本文新算法原理圖

2算法仿真及分析

本文以16QAM信號為實驗仿真信號，平方根升余弦脈沖濾波器(主要作用是內插成形)的滾降因子為0.5，上采樣為4。功放模型采用Saleh模型，多項式模型(預失真器模型)采用的數學模型下：

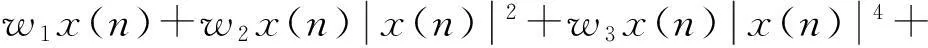
(15)

其中w1、w2、w3、w4為預失真器待更新的權系數。

預失真器的性能由歸一化均方誤差(NMSE)、輸出信號功率譜特征(帶內失真和帶外抑制兩個方面)、誤差矢量幅度(EVM)和計算復雜度來衡量。其中EVM是全面衡量通信系統性能的一個重要指標。NMSE的表達式為：

(16)

EVM的表達式為：

(17)

其中，Sideal為參考信號，Smeas為實際測量信號。

當迭代次數小于100時，采用RLS算法，當迭代次數大于100時，采用NLMS算法，得到的仿真結果為：

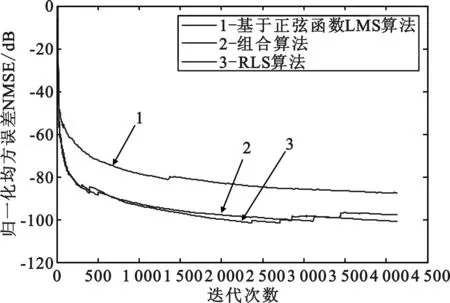
圖4　不同自適應算法的NMSE曲線

收斂算法無預失真RLS+NLMSRLSNLMSLMSEVM0.55520.00240.00230.00820.0260

從仿真結果可以看出，NLMS和LMS算法預失真性能較差，RLS和新的組合算法的預失真性能基本一樣，但是組合算法的復雜度卻大大低于RLS算法。

3結語

預失真算法是影響預失真性能重要因素，常用的自適應算法有RLS算法和LMS算法。RLS算法收斂速度快，收斂性能好；LMS算法計算復雜度低，但是收斂性能有限。在學習RLS和LMS算法的基礎上，本文提出了一種RLS和基于正弦函數的歸一化LMS相結合的算法，在初始階段利用RLS算法進行快速收斂，當誤差趨于穩態時，采用復雜度低的LMS。仿真結果表明，這種組合算法的預失真性能好，復雜度較低，加快了收斂速度。

參考文獻：

[1]陳斌，任國春，龔玉萍.基于多項式與查找表的預失真技術研究[J].信息安全與通信保密，2011(3)：44-46.

CHEN Bin, REN Guo-chun, GONG Yu-ping. Study on Pre-Distortion Technique based on Polynomial and Look-Up Table[J]. Information Security and Communications Privacy, 2011(3)：44-46.

[2]Haykin S. Adaptive Filter Theory[P]. Prentice-Hall, 2002.

[3]周志文, 高俊, 屈曉旭. 變步長 LMS 算法預失真仿真與實現[J]. 通信技術, 2013(9): 032.

ZHOU Zhi-wen, GAO Jun, QIU Xiao-xu. Simulation and Implementation of Polynomial Pre-Distortion based on Variable-Step LMS Algorithm[J]. Communications Technology, 2013(9):32.

[4]Blumenstein J. The Impact of the Saleh Nonlinearity on the 2D Spreading based System Signals with High Envelope Fluctuations. In: Proceedings of IEEE ICECOM, Dubrovnik, 2010:1-4.

[5]李曉艷，聶明新，余文芳. 一種變步長LMS自適應算法噪聲抵消算法研究[J].武漢理工大學學報，2010,3(4)：547-549.

LI Xiao-yan, NIE Ming-xin, YU Wen-fang. A Variable Step Size LMS Adaptive De-Noising Algorithm[J]. Journal of Wuhan University of Technology, 2010,3(4)：547-549.

[6]沈大偉, 賀思, 李正宙等. 一種改進的變步長變更新速率 LMS 自適應濾波算法及仿真[J]. 電子質量, 2010 (12): 11-12.

SHEN Da-wei, HE Si, LI Zheng-zhou，et al. A Modified Variable Step Size and Multi-Rate Updated LMS Adaptive Filtering Algorithm and Its Simulation [J]. Electronics Quality, 2010 (12): 11-12.

[7]張銀行，楊輝媛，宋志國. 基于歸一化LMS算法的自適應濾波器設計[J].吉首大學學報， 2012，33(2)：80-83.

ZHANG Yin-hang, YANG Hui-yuan, SONG Zhi-guo. Design of Adaptive Filter based on the Normalized Least-Mean-Square Algorithm[J]. Journal of Jishou University, 2012，33(2)：80-83.

[8]PAN W S, LIU Y, TANG Y. A Pre-Distortion Algorithm based on Accurately Solving the Reverse Function of Memory Polynomial Model. IEEE Wireless Communication Letters, 2012, 1(4):384-387.

[9]盧炳乾, 馮存前, 龍戈農. 一種基于正弦函數的歸一化變步長 LMS 算法[J].無線電工程, 2014, 44(3): 21-23.

LU Bing-qian, FENG Cun-qian, LONG Ge-nong. A Normalized Variable Step-Size LMS Algorithm based on Sine Function [J]. Radio Engineering, 2014, 44(3): 21-23.

韓冰(1990—)，女，碩士，主要研究方向為功放線性化技術；

晉東立(1963—)，男，研究員，主要研究方向為航天通信。

Parameters Identification Algorithm of Digital Pre-Distorter Model

HAN Bing，JIN Dong-li

(Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China)

Abstract：Digital baseband pre-distortion is one of the most efficienct ways to compensate nonlinearity of the power amplifier, and the choice of adaptive algorithm directly affects,to a large extent,the pre-distortion performance of the system. LMS and RLS are the most frequently-used adaptive convergence algorithms,and based on the analysis of their advantages and disadvantages, a novel algorithm combined with sine function-based normalized LMS and RLS is proposed. Simulation results indicate that this combined algorithm could enormously lower computational complexity while maintaining the same pre-distortion precision as RLS.

Key words：power amplifier; digital pre-distortion; sine function; normalized LMS; RLS; variable step

作者簡介：

中圖分類號：TN927

文獻標志碼：A

文章編號：1002-0802(2015)07-0799-04

收稿日期：*2015-03-13；

doi:10.3969/j.issn.1002-0802.2015.07.010