一種基于插值的定時同步算法研究*

文申平，王永斌，付天暉，張　龍

(海軍工程大學 電子工程學院，湖北 武漢 430033)

?

一種基于插值的定時同步算法研究*

文申平，王永斌，付天暉，張龍

(海軍工程大學 電子工程學院，湖北 武漢 430033)

修回日期：2015-05-30Received date:2015-02-03；Revised date：2015-05-30

摘要：基于MSK調制通信系統，采用四階差分定時誤差檢測算法對基于插值的定時同步環路進行了研究和分析，并提出了一種以插值輸出信號均方誤差最小為準則的插值濾波器設計，提高濾波器輸出精度，改善定時同步環路同步性能。通過MATLAB仿真驗證，與Lagrange插值濾波器相比，基于最小均方插值的定時同步算法，跟蹤階段定時抖動小，對噪聲具有抑制作用，在信噪比較低的情況下也具有較好的同步性能。

關鍵詞：定時同步；最小均方誤差準則；插值濾波器；MSK調制

0引言

在數字通信系統中，由于信道傳輸時延以及收發兩地時鐘偏移，使采樣無法在最佳采樣時刻進行，導致采樣到的信息與發送端的符號信息存在偏差，為了正確恢復出發送端的符號信息，必須做到碼元定時同步。傳統的接收機采用同步采樣方式，利用定時誤差信號直接調整接收端采樣時鐘的相位，實現碼元的定時同步和判決；而全數字接收機采用異步采樣方式，即采樣時鐘和符號時鐘相互獨立，這種情況下，判決取樣的最佳時刻不能通過直接取樣獲得，必須通過插值運算從采樣到的信號樣本值中恢復出來。

本文采用四階差分定時誤差檢測算法[1]對基于插值的定時同步環路進行了簡要的研究與分析，結合輸入MSK信號特點，設計了一種以插值輸出信號均方誤差最小為準則，基于多項式的插值濾波器，并結合定時誤差檢測算法基于插值的定時同步環路進行仿真驗證。實驗結果表明基于最小均方插值的定時同步算法具有更優的同步性能。

1基于插值的定時同步環路

根據文獻[2]的結論，利用插值運算可以從非同步采樣序列中恢復最佳采樣點值。圖1為基于插值的碼元定時同步結構框圖。

假設x(t)為經下變頻后的MSK基帶信號，碼元周期為Ti。在滿足Nyquist定理的條件下，以固定時鐘Ts作為采樣間隔采樣得到時域離散信號x(mTs)。由于信道時延的存在，要得到與發送端同步的最佳采樣序列，需要將A/D轉換信號輸入定時同步環路，由定時控制環路提取定時信息，插值濾波器進行插值修正，即輸出y(kTi)。

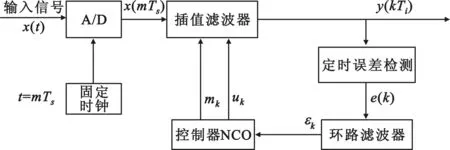
圖1定時同步結構框

定時同步環路包括一個插值濾波器和定時控制環路。插值濾波器從采樣序列中恢復最佳采樣時刻采樣值，是整個定時同步的關鍵。定時控制環路包括定時誤差檢測器(TED)、環路濾波器(LPF)和數控振蕩器(NCO)，向插值濾波器提供定時參數，確定內插基點和插值輸出時各時刻信號的權值。

1.1插值濾波器

插值濾波器是碼元定時同步結構中重要組成部分，其輸入輸出方程[3]為：

y(kTi)=y[(mk+uk)Ts]=

(1)

式中，mk=INT[kTi/Ts]，uk=kTi/Ts-mk，其中，稱mk為插值基點，uk為最佳采樣時刻與基點之間的分數間隔。從式(1)可以看出，基于非同步信號利用插值運算近似求解采樣值y(kTi)的過程，實際上即是對以時刻mk為中心的一組非同步采樣序列{x(mTS)}進行加權求和，而權值為模擬濾波器h(t)的一組采樣值，這組采樣值均與輸入uk有關。由于uk是時變函數，每求一個輸出值就必須事先估計一組濾波器系數，因而在基于信號插值的定時同步實現方案中，多采用基于多項式的插值方法。基于多項式的插值濾波器輸出如下：

(2)

1.2定時誤差檢測(TED)

本文基于最小頻移鍵控(Minimum shift keying，MSK)調制通信系統，對于最佳采樣時刻和采樣時鐘相位誤差的估算，采用四階差分定時算法，該方法基于連續相位調制信號經過Mth階非線性變換，其輸出含有與碼元速率相關的周期分量的性質推導的。公式如下：

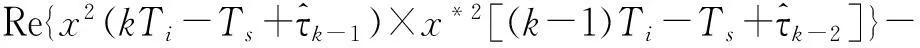
(3)

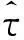
該算法不需借助數據輔助和反饋判決，對MSK、GMSK調制信號具有較好的同步性能。且該算法不受載波頻偏與相偏的影響，因此定時同步環路可以先于載波同步進行，減少載波同步過程的運算量。

1.3環路濾波器(LPF)

當定時控制環路存在噪聲干擾時，可以通過環路濾波器濾波，排除干擾，降低環路噪聲對時鐘相差估計的影響。環路濾波器設計一般采用常用的比例積分結構。其傳遞函數在z域上可以表示為：

(4)

在離散時域下等價的遞歸方程為：

y(k)=y(k-1)+K1×[x(k)-x(k-1)]+K2×x(k)

(5)

K1、K2為環路增益,其取值視具體情況而定。

1.4數控振蕩器(NCO)

數控振蕩器實際是一個相位遞減器，主要由兩部分組成，第一部分是相位溢出控制，即對NCO寄存器中的時延偏置值進行限幅，調用公式[4]為η(m)=[η(m-1)-W(m-1)]mod1，使其只能在0至1之間翻轉，同時，NCO寄存器值每翻轉一次，即相位值每溢出一次，意味插值基點mk的一次確立。第二部分是分數間隔計算，uk=η(mk)/W(mk)，W(mk)為受碼元同步環路控制的步進控制字，其中，W(mk)=wεk，w為一小的常數，εk為環路濾波器輸出信號。mk和uk的確立，為插值濾波器確立了近似最佳采樣時刻。

2MMSE插值濾波器設計

插值濾波器是碼元定時同步模型中的關鍵。本文插值濾波器的設計利用輸入信號的特點，基于多項式的改進插值濾波器，以插值輸出信號與理想最佳時刻采樣值之間均方誤差最小為準則。MSK調制信號具有包絡恒定、相位連續的特點，其正交表達式[5]為：

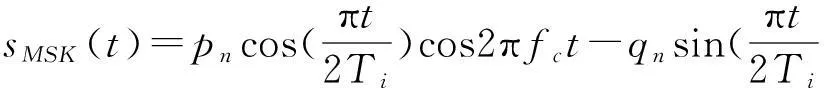
(6)

式中，pn=cos(φn)=±1，qn=Incos(φn)=±1。由文獻[6]MSK信號可等效為經過半波整型的偏移正交PSK(OQPSK)或交錯正交PSK(SQPSK)。則下變頻后接收信號可表示為：

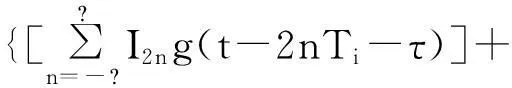
(7)

式中，g(t)為余弦脈沖，有：

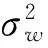
(8)

由于插值濾波器的非理想性和定時同步估計的誤差，導致所需的同步采樣信號yp(kTi+τ)與插值修正后的序列yp[(mk+uk)Ts]之間存在差異。其中定義定時同步估計的誤差為：

kTs=(mk+uk)Ts-(kTi+τ)

(9)

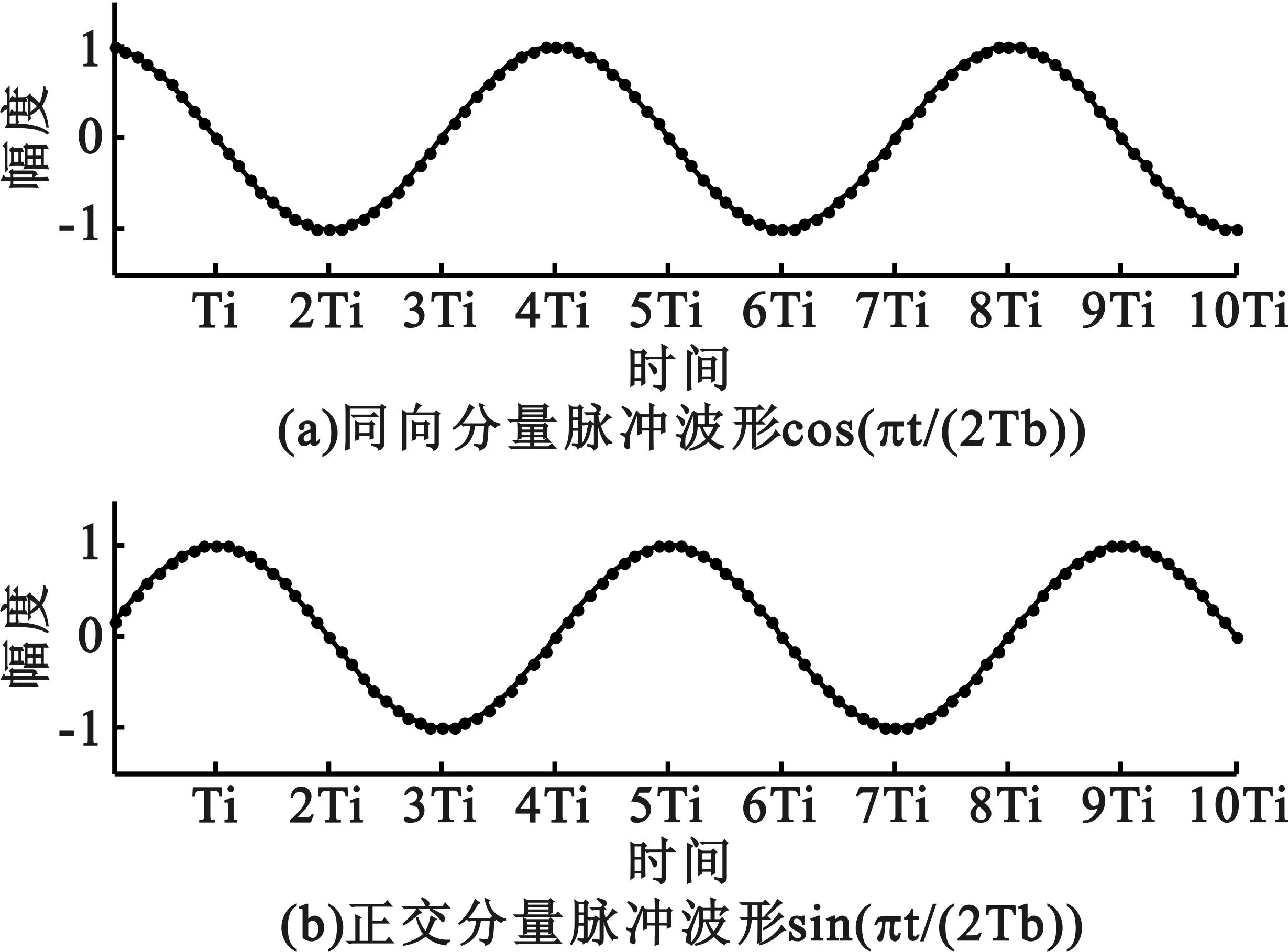
圖2MSK信號分量脈沖波形

可以從式(2)、式(8)、式(9)得到：

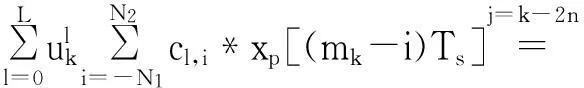
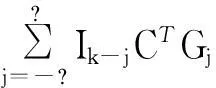
(10)

這里，

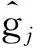
C=(c0,-N1c1,-N1c2,-N1…cL-1,N2)T，

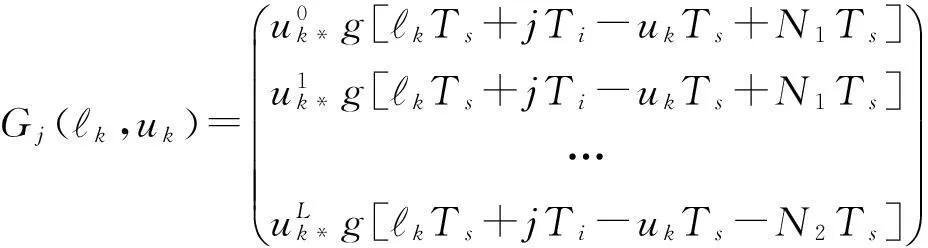
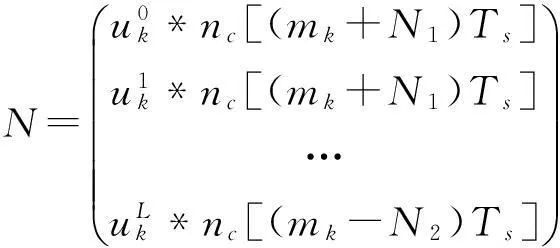
由高斯白噪聲與輸入信號的數理統計特性，定義接收機的輸出均方誤差為：

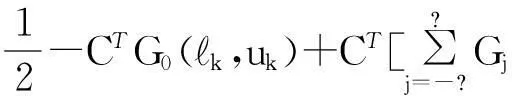
(11)

式中，RN=E(NNT)。

假定不存在定時估計誤差，并根據文獻[7]所提到的優化方法，構建關于濾波器系數序列C的代價函數如下：

(12)

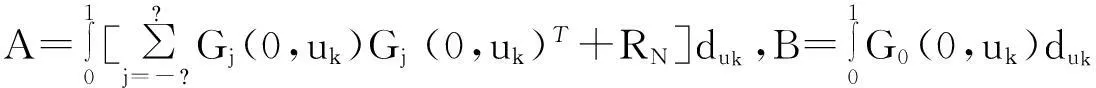
3仿真與分析

為驗證上述算法正確性，基于MATLAB構建如圖1所示基于插值的定時同步系統，在高斯白噪聲信道下，MSK調制方式，采用與三階Lagrange插值濾波器相近復雜度的三階MMSE插值濾波器，固定采樣時鐘Ts=0.1Ti，環路濾波器系數為K1=1/512，K2=1/256，信道時延設為0.5Ti，此時碼元判決受碼間串擾影響最大。

圖3為固定信噪比SNR=10 dB時，基于不同插值濾波器下定時同步時鐘相差跟蹤性能仿真曲線。

(a)MMSE插值

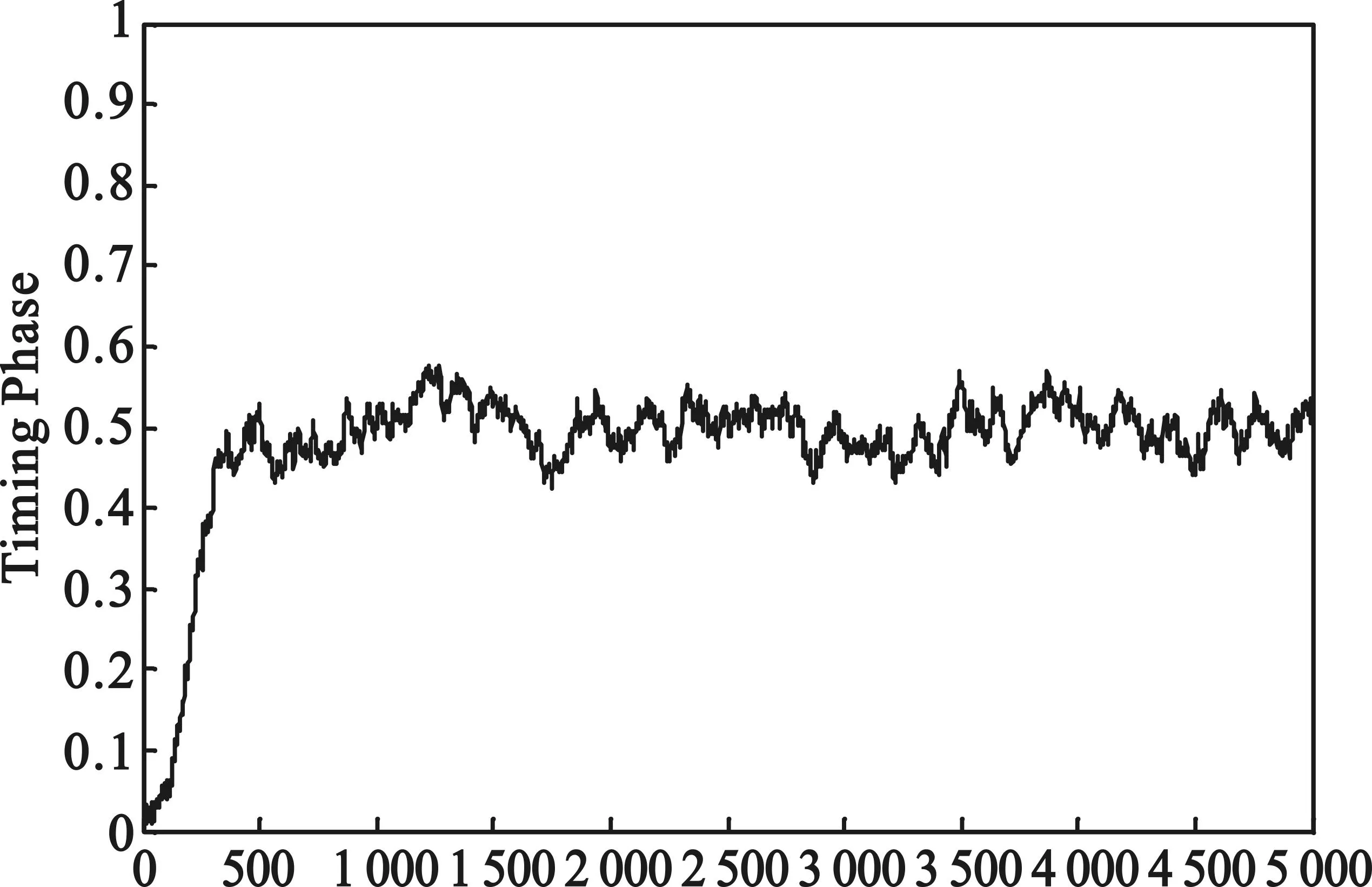
(b)Lagrange多項式插值

圖4為在不同信噪比下，基于不同插值濾波器下定時同步算法誤碼率仿真曲線，符號序列為105個。

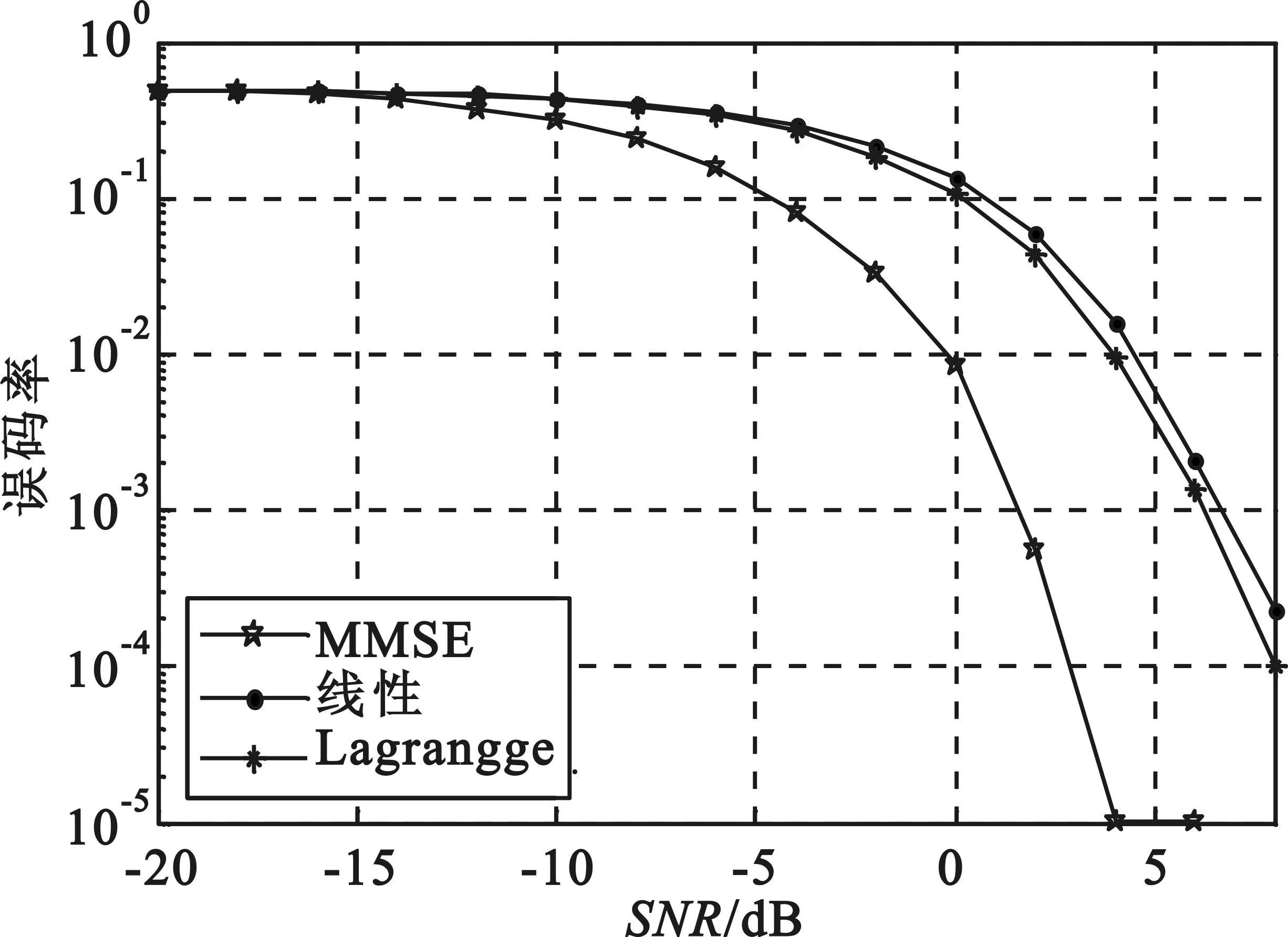
圖4　不同插值定時同步算法性能仿真

圖3給出了在有加干擾情況下不同插值濾波定時同步時鐘相差估計性能曲線，在捕獲時間相近的情況下，MMSE插值定時同步性能曲線更加平穩，穩態定時抖動更小，具有更好的收斂精度。這也與理論推倒相一致，因為MMSE插值濾波器考慮了噪聲的因素。圖4給出了不同插值濾波定時同步算法下誤碼率仿真曲線，基于MMSE插值的誤碼率仿真曲線明顯更優，在信噪比較低情況下也具有較好同步性能。

4結語

本文提出了一種基于最小均方誤差準則的插值濾波器與定時誤差檢測算法結合的碼元定時同步算法，其利用四階差分定時誤差檢測算法與環路濾波器提取定時誤差信息，經數控振蕩器確定插值相位，由最小均方插值運算恢復最佳采樣值。仿真結果表明，基于最小均方插值的定時同步算法具有良好的性能，對噪聲引起的定時抖動具有良好的抑制作用，與拉格朗日插值定時同步相比，降低了信噪比門限，在較低信噪比下也具有良好同步性能。

參考文獻：

[1]Andrea N D A, Mengali U, Reggiannini R. A Digital Approach to Clock Recovery in Generalized Minimum Shift Keying[J].IEEE-Trans.Veh.Echnol.1993(39):227-234.

[2]Gardner F M.Interpolation in Digital Modems-Part I: Fundamentals[J]. IEEE-Trans Commum.1993, 41(3):501-507.

[3]張公禮.全數字接收理論與技術研究[M].北京：科學出版社,2005.

ZHANG Gong-li. All Digital Receiver Research on Theory and Technology[M].Beijing: Science Press,2005.

[4]劉旺，朱江，付永明等.一種并行的定時同步環路實現研究[J].通信技術，2013，46(10)：1-5.

LIU Wang, ZHU Jiang, FU Yong-ming,et al.A Novel Interpolator Controlling Scheme in High-Speed Digtal Timing Recovery Loop[J].Communications Technology, 2013，46(10)：1-5.

[5]施意，張爽，張昕.大氣噪聲對甚低頻通信系統干擾仿真分析[J].通信技術，2013，46(09):32-34.

SHI Yi, ZHANG Shuang, ZHANG Xin. Simulation and Analysis of Almospheric Noise Interference on VLF/LF Communication[J]. Communications Technology, 2013,46(09):32-34.

[6]黃載祿，殷蔚華，黃本雄.通信原理[M].北京：科學出版社，2007.

HUANG Zai-lu, YIN Wei-hua, HUANG Ben-xiong. Principle of Communication[M].Beijing: Science Press,2007.

[7]LI Han,LU Cheng-You,WANG Qin. Optimal Farrow Coefficients for Timing Recovery in QAM Demodulation Receiver[J]. IEEE Sarnof Symposium,2006(37):356-359.

文申平(1991—)，男，碩士研究生，主要研究方向為數字通信理論與技術；

王永斌(1961—)，男，教授，碩士，主要研究方向為數字通信，通信信號處理；

付天暉(1981—)，男，博士，講師，主要研究方向為數字通信，通信信號處理；

張龍(1991—)，男，碩士研究生，主要研究方向為數字通信理論與技術。

Interpolation-based Timing Synchronization Algorithm

WEN Shen-ping, WANG Yong-bin, FU Tian-hui, ZHANG Long

(College of Engeineering, Naval University of Enginnering, Wuhan Hubei 430033, China)

Abstract：Based on MSK (Minimum Shift Keying) communication system, four-order differential algorithm of timing error detection is applied to researching and simulating interpolation-based timing synchronization loop, and a design on interpolation filter with minimum mean square error of interpolation output signal is proposed to improve the accuracy of filter and the performance of timing synchronization loop. MATLAB simulation indicates that, compared with the Lagrange interpolation filter, the timing synchronization based on MMSE (Minimum Mean Square Error) interpolator enjoys small timing jitter in tracking process, and is of better anti-jamming ability and better synchronization performance in low SNR condition.

Key words：timing synchronizer; MMSE; interpolation filter; MSK modulation

作者簡介：

中圖分類號：TN911.22

文獻標志碼：A

文章編號：1002-0802(2015)07-0780-04

收稿日期：*2015-02-03；

doi:10.3969/j.issn.1002-0802.2015.07.006