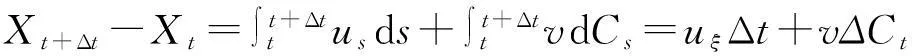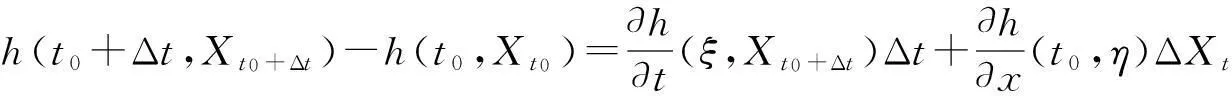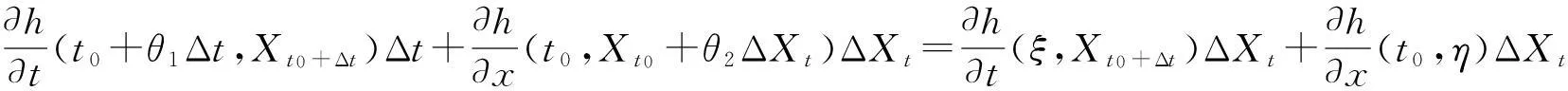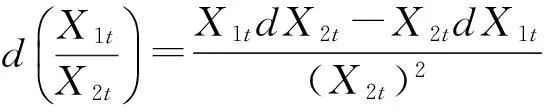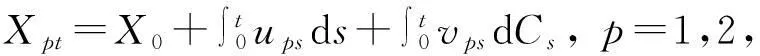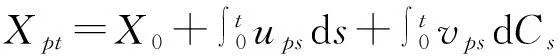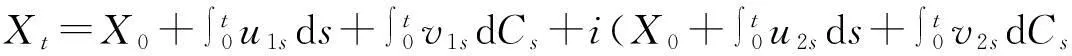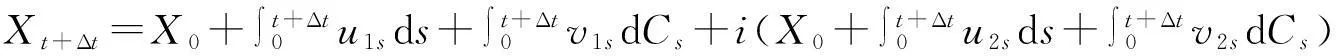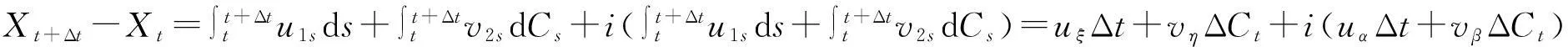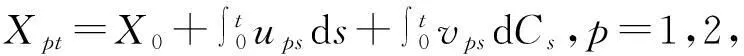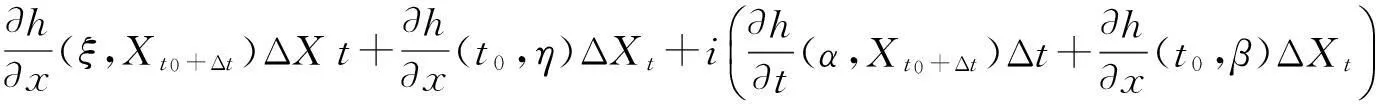模糊微分的性質

尤翠蓮，王偉卿

(河北大學 數學與信息科學學院，河北保定　071002)

模糊微分的性質

尤翠蓮，王偉卿

(河北大學 數學與信息科學學院，河北保定071002)

摘要：在求解由劉過程驅動的模糊微分方程時，需要研究一類新的模糊微分(劉微分)的性質. 給出了模糊微分的2個中值定理和4個模糊微分公式， 并且將這些結論推廣到復模糊微分的情形. 這些工作為模糊微分方程理論的完善和應用奠定了基礎.

關鍵詞：模糊過程；模糊微分； 中值定理； 復模糊過程

DOI：10.3969/j.issn.1000-1565.2015.02.001

中圖分類號：O159

文獻標志碼：志碼：A

文章編號：編號：1000-1565(2015)02-0113-05

Abstract:To solve fuzzy differential equation driven by Liu process， some properties of a new kind of fuzzy differential (Liu differential) are needed. Two mean value theorems of fuzzy differential and four fuzzy differential formulas are given in this paper. Furthermore， these conclusions are extended to the case of complex fuzzy process. The studies above lay a theoretical foundation for calculation and application of the fuzzy differential equation.

收稿日期:2014-10-08

基金項目：國家自然科學基金資助項目(11201110；61374184；11101115)； 河北省高等學校優秀青年基金資助項目(Y2012021)

Properties of fuzzy differential

YOU Cuilian， WANG Weiqing

(College of Mathematics and Information Science， Hebei University， Baoding 071002， China)

Key words: fuzzy process； fuzzy differential； mean value theorem； complex fuzzy process

MSC 2010: 34A07

第一作者:尤翠蓮(1977-)，女，河北唐山人，河北大學副教授，博士，主要從事不確定理論與模糊微分方程的研究.

E-mail：yycclian@163.com

在實際生活中， 隨機事件通常用概率來描述.1965年Zadeh[1]給出了模糊事件的定義. 為了度量模糊事件， Zadeh[2]在1978年引入了可能性測度. 后來Nahmias[3]， Yanger[4]， De Cooman[5]， Dubois等[6]做了進一步的研究. 然而可能性測度沒有自對偶性， 因此在2002年Liu 等[7]引入了可信性測度的概念， 并且Li等[8]給出了可信性測度的一個充分必要條件， Liu[9]提出了可信性理論.

為了處理動態隨機現象， 隨機過程已經被廣泛應用. 要處理動態模糊現象， 同樣也需要相應的計算，因此在2008年Liu[10]提出了模糊過程、微分公式和模糊積分， 之后被更名為劉過程、 劉公式和劉積分. 后來，You等[11]將劉過程、 劉公式和劉積分推廣到多維的情形. Qin[12]對復劉過程、復劉公式和復劉積分進行了研究. 尤翠蓮等[13]研究了劉積分的性質以及積分存在的條件.劉過程的更多內容可參見文獻[14-19].

不管求解模糊微分方程， 還是用模糊微分方程解決實際問題， 前提都是要研究模糊微分的性質. 本文旨在對模糊微分及復模糊微分的性質進行研究.

1預備知識

設Θ為一個非空集合，P為Θ的非空冪集，Cr為可信性測度，A為P中的事件，Cr{A}用來衡量事件A發生的可能性大小，為了保證Cr{A}的數學性質，可信性測度Cr需滿足如下條件：

1)(正則性)Cr{Θ}=1;

2)(單調性)當A?B時，Cr{A}≤Cr{B}；

3)(自對偶性)當A?P時，Cr{A}+Cr{Ac}=1；

4)(極大性)對于任意的Ai?P， 如果supiCr{Ai}<0.5， 那么Cr{∪iAi}=supiCr{Ai}.

Liu[9]稱三元組(Θ，P，Cr)為可信性空間. 從可信性空間到實數集的函數就是模糊變量.

定義1[10]劉過程Ct是指滿足下面3個條件的模糊過程：

1)C0=0；

2)Ct具有獨立增、穩態增性質；

3) 對于固定的時刻t，每一個增量Cs+t-Cs是一個具有期望值et和方差σ2t2的正態模糊變量，其隸屬函數為

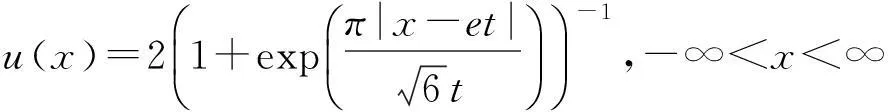
特別地，當e=0，σ=1時，稱這樣的劉過程為標準劉過程.

定理1(劉公式)[10]假設Xt是一個由dXt=utdt+vtdCt給出的模糊過程，Ct是一個標準劉過程，其中ut，vt分別是絕對可積和劉可積的模糊過程，h(t,x)是一個連續可微的函數， 那么Yt=h(t,Xt)也是一個模糊過程， 并且

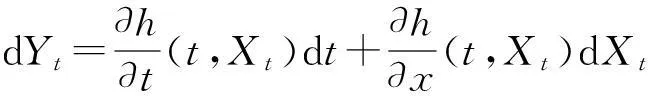
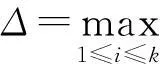
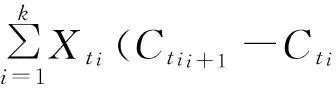
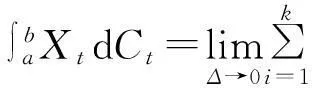
定義3[12]假設T是一個指標集，則一個復模糊過程是一個從T×(Θ,P,Cr)到復數集的函數.

定理2[12]一個模糊過程是復模糊過程的充分必要條件是存在2個實模糊過程X1t，X2t使得Xt=X1t+iX2t， 其中i是虛數單位.

定理3[11]設(C1t,C2t,…,Cmt)T是一個m維標準劉過程，h(t,x1,x2,…,xn)是一個多變量連續可微的函數，n維模糊過程(X1t,X2t,…,xnt)由

給出， 其中upt，vpqt分別是絕對可積和劉可積的模糊過程， 則模糊過程Yt=h(t,X1t,X2t,…,Xnt)的微分為

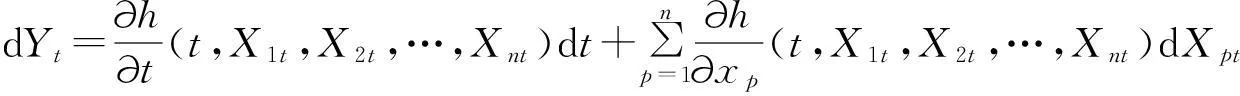
2模糊微分的性質

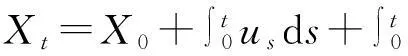
Xt+Δt-Xt=uξΔt+vΔCt.

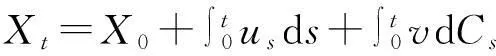
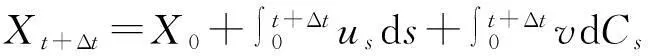
由黎曼積分的中值定理可知，存在時刻ξ(t<ξ

定理5(第2中值定理)設Ct是一個標準的劉過程，h(t,x)是連續可微的函數，dXt=utdt+vtdCt，其中us和vs是絕對可積和劉可積的模糊過程，則Yt=h(t,Xt)也是一個模糊過程， 且

證明：由劉公式可知Yt=h(t,Xt)是一個模糊過程.所以根據微分中值定理可知，存在ξ，η，其中ξ=t0+θ1(t-t0)，η=Xt0+θ2(Xt-Xt0)，0<θ1，θ2<1使得

h(t0+Δt,Xt0+Δt)-h(t0,Xt0)=[h(t0+Δt,Xt0+Δt)-h(t0,Xt0+Δt)]+[h(t0,Xt0+Δt)-h(t0,Xt0)]=

定理6若X1t和X2t是模糊過程，則

1)d(X1t±X2t)=dX1t±dX2t.

證明：取定理3中n=2，h(t,x1,x2)=x1±x2,可得出結論.

2)d(X1tX2t)=X2tdX1t+X1tdX2t.

證明：取定理3中n=2，h(t,x1,x2)=x1x2,可得出結論.

3) 對任意常數c，d(cX1t)=cdX1t.

證明：由劉公式可得出結論.

3復模糊微分的性質

Xt+Δt-Xt=uξΔt+vηΔCt+i(uαΔt+vβΔCt).

其中t<ξ,α,β,η

證明：由于h(t,x)是連續可微的復函數，因此Yt=h(t,Xt)是一個復模糊過程. 所以

h(t0+Δt,Xt0+Δt)-h(t0,Xt0)=[h(t0+Δt,Xt0+Δt)-h(t0,Xt0+Δt)]+[h(t0,Xt0+Δt)-h(t0,Xt0)]=

其中ξ=t0+θ1(t-t0)，η=Xt0+θ2(Xt-Xt0)，α=t0+θ3(t-t0)，β=Xt0+θ4(Xt-Xt0) ，0<θ1,θ2,θ3,θ4<1.

定理9若X1t，X2t，Y1t，Y2t是模糊過程，Xt=X1t+iX2t，Yt=Y1t+iY2t， 則

證明：由定理2和定理6可得出結論.

4結論

本文進一步研究了模糊微分(劉微分)的性質， 給出了模糊微分的2個中值定理，4個模糊微分公式， 以及2個復模糊中值定理和4個復模糊微分公式. 這些性質可簡化求解模糊微分方程的過程.

參考文獻:

[1]ZADEH L A. Fuzzy sets as a basis for a theory of possibility[J]. Fuzzy Sets and Systems， 1987， 1(1): 3-28.

[2]ZADEH L A. Fuzzy sets[J]. Information and Control， 1965， 8(3):338-353.

[3]NAHMIAS S. Fuzzy variables[J]. Fuzzy Sets and Systems， 1987， 1(2):97-110.

[4]YAGER R. A foundation for a theory of possibility[J]. Journal of Cybernetics， 1980， 10(1-3):177-204.

[5]COOMAN De G. Possibility theory I-III[J]. International Journal of General Systems， 1997， 25(4):291-371.

[6]DUBOIS D， PRADE H. Possibility theory: an approach to computerized processing of uncertainty[M]. New York：Plenum，1988.

[7]LIU Baoding， LIU Yankui. Expected value of fuzzy variable and fuzzy expected value models[J]. IEEE Transaction on Fuzzy Systems， 2002， 10(4):445-450.

[8]LI Xiang， LIU Baoding. Chance measure for hybrid events with fuzziness and randomness[J]. Soft Computing， 2009， 13(2):105-115.

[9]LIU Baoding. Uncertainty theory: an introduction to its axiomatic foundations[M]. Berlin：Springer-verlag， 2004.

[10]LIU Baoding. Fuzzy process， hybrid process and uncertain process[J]. Journal of Uncertain Systems， 2008，2(1):3-16.

[11]YOU Cuilian，HUO Huae， WANG Weiqing. Multi-dimensional Liu process，differential and integral[J]. Journal of East Asian Mathematical， 2013，29(1):13-22.

[12]QIN Zhongfeng. On analytic function of complex Liu process.[EB/OL].(2008-04-12) [2013-10-02]. http://orsc.edu.cn/process/071026.pdf，2007.

[13]尤翠蓮， 王根森. 一類新的模糊積分的性質[J]. 河北大學學報：自然科學出版社， 2011， 31(4):337-340.

YOU Cuilian， WANG Gensen.Properties of a new kind of fuzzy integral[J].Journal of Hebei University：Natural Science Edition， 2011， 31(4):337-340.

[14]ZHU Yuanguo. Fuzzy control theory[EB/OL]. ( 2008-07-05) [ 2013-10-02]. http://orsc.edu.cn/~yhzhu/fct.pdf.

[15]ZHU Yuanguo. Fuzzy optimal control with application to portfolio selection[EB/OL]. ( 2008-01-17) [2013-10-02]. http://orsc.edu.cn/process/080117.pdf.

[16]LIU Linzhong， LI Yinzhen. The fuzzy quadratic assignment problem with penality: new models and genetic algorithm[J]. Applied Mathematics and Computation， 2006， 174(2):1229-1224.

[17]LIU Yankui， LIU Baoding. Random fuzzy programming with chance measures defined by fuzzy integrals[J]. Mathematical and Computer Modelling， 2002，36(4-5):509-524.

[18]LIU Baoding， LIU Yankui. Expected value of fuzzy variable and fuzzy expected value models[J]. IEEE Transactions on Fuzzy Systems， 2002，10(4):445-450.

[19]QIN Zhongfeng， LI Xiang. Option pricing formula for fuzzy financial market[J]. Journal of Uncertain Systems， 2008， 2(1): 17-21.

(責任編輯：王蘭英)