遺傳算法優化模糊PI的網側變流器的控制

張 蕾，劉小河

（北京信息科技大學 自動化學院，北京 100192）

隨著近幾十年風力發電技術的快速發展，相對傳統的恒速恒頻發電技術已經逐漸被對風能利用更高效的變速恒頻風力發電技術所替代。在變速恒頻風力發電系統中，雙饋電機已經成為主流機型，而在雙饋風力發電系統中，網側變流器的主要功能是實現網側輸入功率因數和保持直流環節穩定，從而保證機側變流器甚至于整個雙饋系統的可靠工作[1]。因此，對于網側變流器的控制十分關鍵。

目前，傳統的DFIG網側PWM變流器的控制器都采用經典的比例積分（PI）控制，但PI控制抗擾動性能有些不足，尤其在電網波動的情況下，其系統的動態性能和魯棒性有些缺陷。近年來，也有很多新的控制方法被陸續提出[2]。文獻[3-4]先將正負序電流分離后接著進行雙閉環PI控制；文獻[5-6]基于變結構的滑模控制理論提出了新的控制方法，系統的魯棒性得到很大提高，但滑模控制產生抖振現象也是一個重要的不穩定因素；文獻[7]利用定頻模型預測控制的方法實現對參考電流的準確跟蹤。

本文在基于傳統方法的基礎上，提出基于遺傳算法優化的模糊PI控制方法，來提高系統的動態性能，其基本思想為，對模糊控制器的隸屬度函數用遺傳算法進行尋優，將優化后的模糊PI控制器應用到電壓外環和電流內環，同時利用負載電流的前饋補償，提高系統的抗干擾能力。

1 DFIG網側PWM變流器模糊控制器的設計

1.1 網側變流器模糊控制器的設計

1）電流內環控制器設計

由于d軸與q軸電流的對稱性，因此以d軸為例設計控制器。整流器用代替，考慮到典型Ⅰ型系統抗干擾能力較差以及電動勢擾動對輸出的影響，所以這里采用了抗干擾性能強的典型Ⅱ型系統設計。Ts為內環電流采樣周期，KPWM為等效增益系數，L為電網進線電感，R為電網進線電阻，τi=L/R。電流內環控制框圖如圖1所示。

圖1 d軸電流結構Fig.1 Diagram of d-axis current structure

可推出電流內環開環傳遞函數為

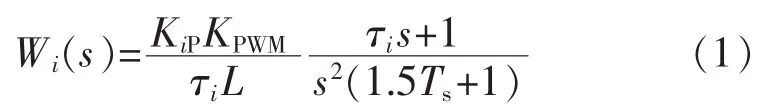
可得

由上式得到比例和積分增益

2）電壓外環控制器設計

為了便于對電壓外環的分析，可以把電流內環按典型I型系統等效為

查閱文獻[8]可知直流側的電流Idc和交流電流的有效值Im之間的關系為

電壓外環控制結構如圖2所示。

圖2 電壓外環結構Fig.2 Voltage outer structure diagram

τu為電壓采樣時間常數；Tu為比例調節系數；Ku為積分增益。τu和 Ts合并等效為 Teu=τu+3Ts，可得電壓外環開環傳遞函數為

根據典型Ⅱ型系統的參數關系，令Tu=hTcm得：

一般工程上h=5，可得PI調節參數為

在實際調試過程中需要對參數適當修改，以達到要求。

1.2 模糊控制器的設計

傳統雙閉環控制系統中PI參數是恒定的，但在實際風力發電系統中，系統模型會隨著條件變化而變化，PI參數如果保持不變，系統動態性能就會變差，模糊控制對數學模型要求不高，魯棒性較好。因此將模糊控制器引入網側變流器的電流內環和電壓外環，與PI控制器結合。偏差比較大時，先用模糊控制的方法，使系統較快穩定；偏差比較小時，利用PI控制消除穩態誤差。控制框圖如圖3所示。

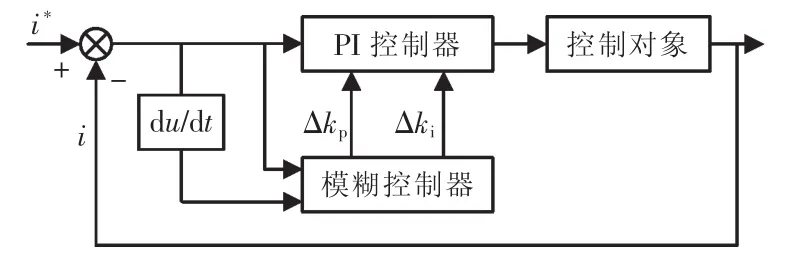
圖3 模糊PI控制Fig.3 Fuzzy PI control block

以電流的dq分量為例，采用雙輸入雙輸出系統，輸入量為電流的偏差e和電流的偏差變化率Δe，輸出為 PI參數的變化量 Δkp、Δki。 則 PI控制器輸出參數為

kp′、ki′為預整定值。

本文模糊論域采取7個，中間5個子集采用三角形隸屬度函數，最左NB選取了Z型函數，最右PB選取了S型隸屬度函數，采取實數編碼的方式進行編碼。示意圖如圖4所示。

圖4 模糊劃分示意Fig.4 Fuzzy partition schematic

根據實驗以及專家經驗指定的模糊規則表1所示。

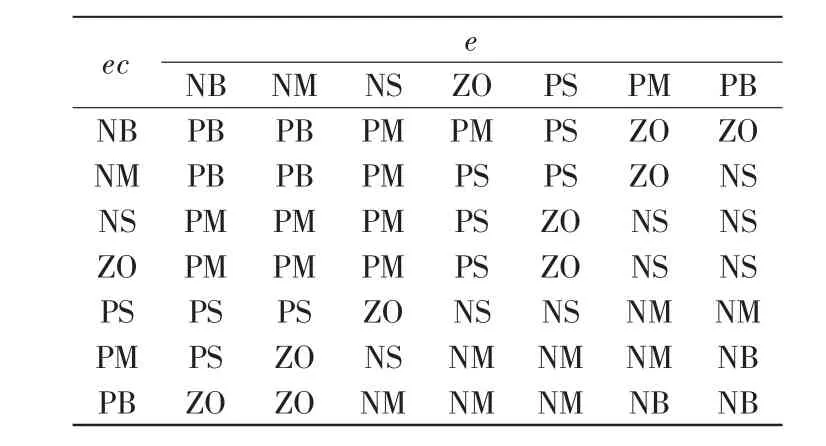
表1 Kp的模糊規則表Tab.1 Fuzzy rule table of Kp

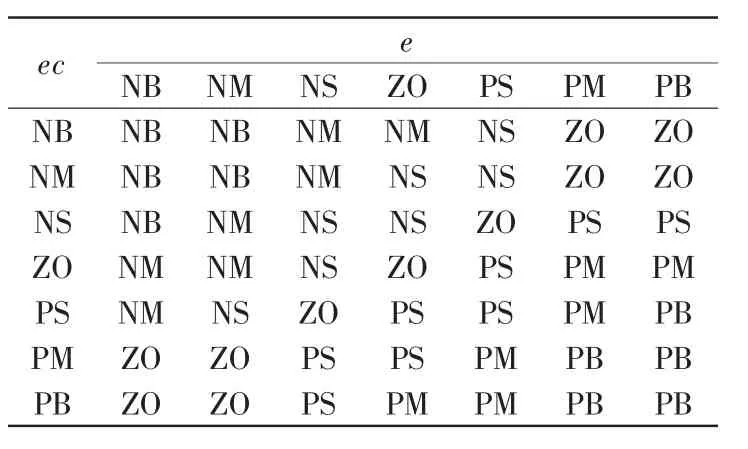
表2 Ki的模糊規則表Tab.2 Fuzzy rule table of Ki

2 基于遺傳算法優化的模糊PI控制器的設計

2.1 遺傳算法對模糊PI控制器的優化

遺傳算法對于模糊控制器一般都是針對其數據或規則庫來進行的，通常是把系統的某些重要的性能指標作為標準，通過一系列遺傳搜索得到最優的隸屬度函數、模糊控制規則、量化因子等。這里是對隸屬度函數進行了優化[9]。

2.2 遺傳算法優化過程設計

1）隸屬函數的編碼

一般情況下，對隸屬度函數論域的劃分是均勻的，但是在實際控制中對模糊論域的劃分采用不均勻劃分的方法，更可以滿足系統在不同階段的要求。

模糊子集頂點的橫坐標值，左右2個端點到頂點的距離決定了隸屬度函數的形狀。為了減少參數數量，選取了左右對稱的隸屬度函數，要優化的參數是底邊端點間的距離。

2）適應度函數函數的選擇

系統的控制設計必須滿足系統的性能指標，因此可以將性能指標作為適應度函數。這里的約束條件選取了系統的控制量、超調量和系統誤差，以式（6）作為目標函數：

式中：u（t）為控制器輸出；e（t）為系統誤差；e1（t）為被控對象在 t此刻和（t-1）時刻輸出值之差；ω1、ω2、ω3為權值，這里分別取0.98、0.001和2，以便壓制系統超調量。

因為一般遺傳算法要求適應度為最值，所以要對適應度函數進行轉化，求取最大值。目標函數取為

3）選擇操作

輪盤賭法可以提高搜索效率，因此先利用這種方法進行選擇，然后將最佳個體復制到子代中，其余個體按適應度所占的比重進行交叉運算。

4）交叉和變異

標準的遺傳算法采用固定值作為交叉和變異操作的概率值，缺點是不能滿足算法在尋優不同階段的不同要求。在算法初期，個體之間差異大，大一點的交叉概率和小一點的變異概率較為合適。后期隨著個體之間的差異逐漸減小，應該適當降低交叉概率，加大一點變異概率，以確保最優個體被保留。因此，采用自適應的交叉和變異概率，公式為

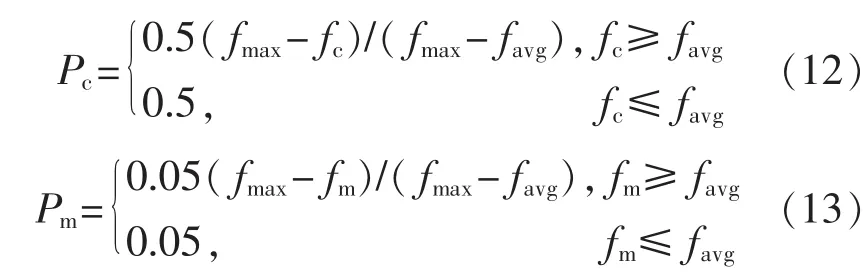
式中：Pc為交叉概率；Pm為變異概率；fmax、favg為此時刻種群的適應度的最大值和平均值；fc，fm分別為要進行交叉運算和變異運算的種群個體的適應度值。

2.3 遺傳算法優化結果

優化后的隸屬度函數如圖5～圖8所示。

圖5 優化后誤差e的隸屬度函數Fig.5 E error membership function after optimization

圖6 優化后的ec的隸屬度函數Fig.6 Ec membership function after optimization

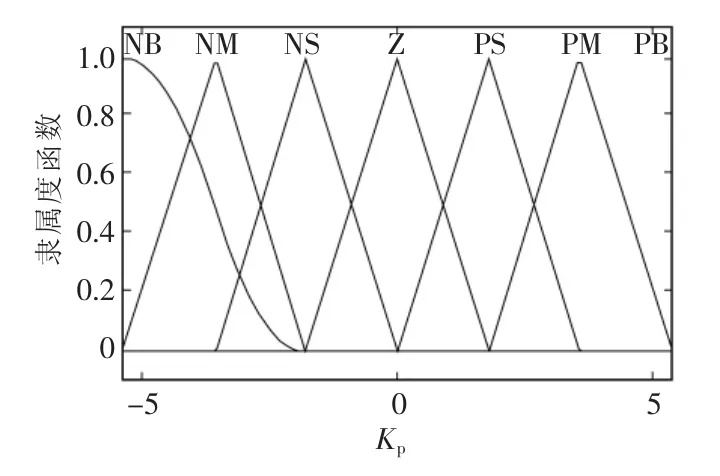
圖7 優化后的ΔKp的隸屬度函數Fig.7 ΔKpmembership function after optimization

圖8 優化后的ΔKi的隸屬度函數Fig.8 ΔKimembership function after optimization

3 系統仿真

在Matlab/Simulink中搭建PWM網側整流器仿真。仿真參數設置如下：交流側的電感L值設為5 mH，交流側的電阻R的值設為0.05 Ω，直流側的電容C的值設為2200 μF，直流電壓 Udc為 600 V，負載 R的值設為10 Ω，采樣時間Ts的值設為0.0001 s。

直流側電壓Udc的仿真波形如圖9所示。

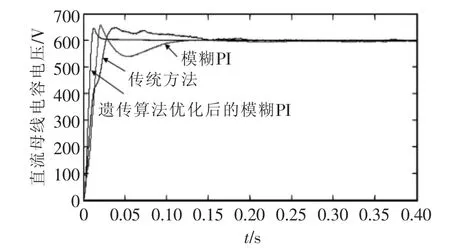
圖9 直流側電壓Udc的仿真波形Fig.9 Simulation of DC voltage waveform

a相電壓電流仿真波形如圖10所示。

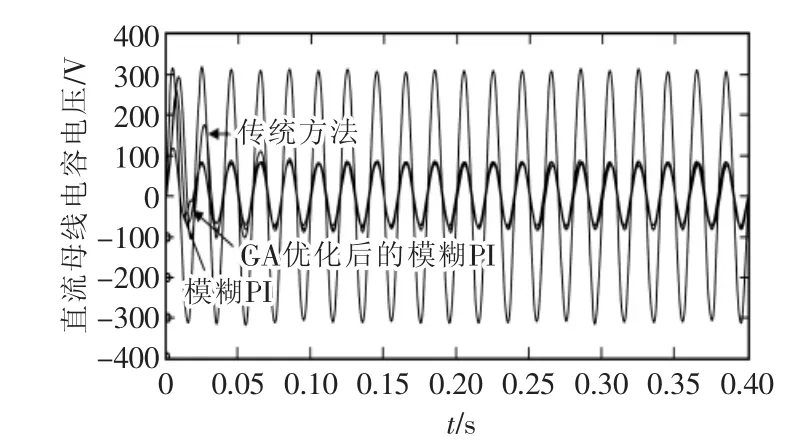
圖10 a相電壓電流仿真波形Fig.10 A phase voltage and current simulation waveforms

由圖9可知，3種方法相比，在超調量上差距不大，但在調節時間上，遺傳算法優化后的模糊PI明顯優于模糊PI和傳統PI，具有響應快，穩定性好的控制性能。從圖10可以看出，新方法的電網電流能更快地穩定，但差距并不大。

在0.3 s處，讓變流器由整流狀態轉換到逆變狀態，其波形如圖11所示。

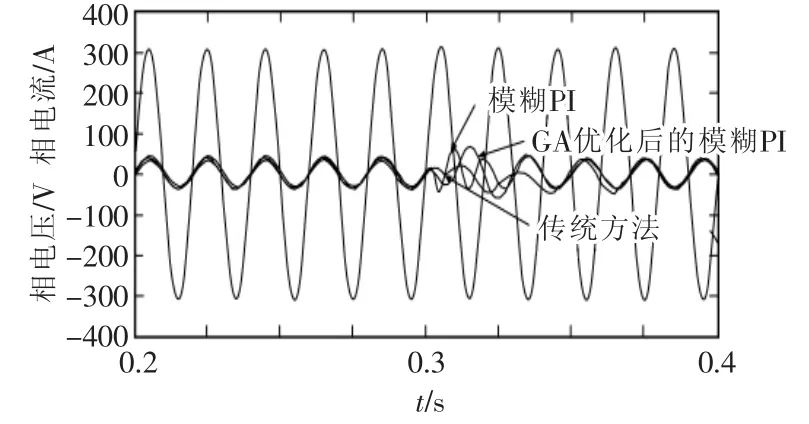
圖11 整流到逆變狀態的a相電流Fig.11 Rectifier state transition to inverter state of a phase current

當變流器由整流狀態過渡到逆變狀態時，GA優化后的模糊PI比傳統PI和模糊PI需要的時間更短，大約為1個周期，模糊PI大約需要1.5個周期，傳統PI需要2～3個周期。

為了測試本文設計控制器的魯棒性，對系統負載施加擾動，仿真結果如圖12所示。R在0.4 s時突然增大1倍。

圖12 負載變化時的直流母線電壓Fig.12 DC-bus voltage when the load changes

采用新方法的直流母線電壓只出現了很小的波動，并且很快趨于穩定，而模糊PI和傳統PI方法從負載變化開始就產生明顯波動，大約0.05 s后逐漸穩定。直流母線電容電壓隨著負載突變變化小，魯棒性好。

4 結語

本文提出的雙饋風力發電系統網側變流器的新控制方法，在電網正常情況下，其響應速度以及系統穩定性明顯優于傳統PI和模糊PI，變流器工作狀態轉換時，新方法適應更快，并且更能適應負載擾動。仿真表明對于提高直流母線電壓的穩定性有比較明顯的效果。

[1]趙清聲，王志新.雙饋風力發電機組系統接入與穩定運行仿真[J].電網技術，2007，22（31）：69-74.

[2]I Erlich，J Kpetschmann，J Fortmann，et al.Modeling of wind turbines based on doubly-fed induction generators for power system stability studies[J].IEEE Transactions on Power Systems，2007，22（3）：909-919.

[3]Pena R.，Cardenas R.，Escobar E.，et al.Control system for unbalanced operation of stand-alone doubly fed induction generators[J].IEEE Transactions on Energy Conversions，2007，22（2）：544-545.

[4]姜衛東，吳志清，李王敏，等.電網不對稱時抑制負序電流并網逆變器的控制策略[J].電工技術學報，2015，30（16）：77-84.

[5]張迪，魏艷君，馬利軒，等.不平衡電網電壓下基于滑模變結構控制的雙饋風電系統網側變流器控制策略[J].電工技術學報，2015，30（10）：266-275.

[6]王萌.電網故障下雙饋風力發電系統功率變換器運行控制[D].天津：天津大學，2012.

[7] 趙振波，李和明.單位功率因數PWM整流器雙閉環PI調節器設計[J].電工技術雜志，2003（5）：68-71.

[8]曹建秋，徐凱.遺傳算法優化的模糊+變論域自適應模糊PID復合控制策略[J].信息與控制，2011，40（1）：44-49.