新型離心葉片設(shè)計方法研究

新型離心葉片設(shè)計方法研究

田曉平1，田琳1，韓濤2

(1.中國飛行試驗(yàn)研究院發(fā)動機(jī)所，陜西西安710089；2. 中國石油西氣東輸管道公司，甘肅銀川751500)

摘要：從控制載荷分布的思想出發(fā)，以葉片的幾何角和半徑的關(guān)系作為加載規(guī)律，提出了加載規(guī)律的參數(shù)化控制思想，發(fā)展了控制葉片加載規(guī)律的設(shè)計方法，使加載規(guī)律的概念更加明確、實(shí)施方法更加簡單有效。為了研究不同加載規(guī)律對葉片性能的影響，首先設(shè)計了幾種具有代表性的加載規(guī)律，對比各種加載規(guī)律，結(jié)果表明：中間加載規(guī)律使得葉片對氣流的加功量主要集中在葉片的中部，為葉片的進(jìn)、出口創(chuàng)造了良好的流動條件，氣流比較穩(wěn)定，流動損失較少，滑移系數(shù)較大，保證有足夠的壓比和較高的效率，抗喘振能力較強(qiáng)，是比較理想的加功方式。

關(guān)鍵詞:離心葉片葉片設(shè)計加載規(guī)律參數(shù)化控制

中圖分類號：TK421.8文獻(xiàn)標(biāo)識碼：A

作者簡介：田曉平(1984-)，男，西北工業(yè)大學(xué)工學(xué)碩士畢業(yè)，現(xiàn)工作于中國飛行試驗(yàn)研究院，發(fā)動機(jī)所。

收稿日期：2015-03-09

Research on design method of a new centrifugal impeller

TIAN Xiaoping，TIAN Lin，HAN Tao

Abstract:For centrifugal impeller, as one of the key factors which determine the impeller’s performance, the geometry shape of blade is closely related to the loading rule of the load on the blade, hence the loading rule is expressed by the relationship between the geometry angle and the radius of blade in this paper. And then based on the idea of controlling the load distribution, this paper proposes the parameterized controlling method for the loading rule, and develops the designing approach of controlling the blade loading rule, which is clearer in concept and simpler in implementation.In order to study the influence of different loading rules on the impeller performance, several representative loading rules are devised, the comparison shows that: the middle rule are relatively suitable loading rules, which make the work done by impeller gather at the middle part of blade, and then create an excellent flow condition for the blade inlet and outlet, leading to stable flow field, less flow losses and greater slip coefficient and guaranteeing sufficient pressure ratio.

Keywords:centrifugal impeller; blade design; loading rule; parameter control

0引言

離心葉片是離心壓縮機(jī)至關(guān)重要的部件之一[1]，它用來壓縮氣體，將壓氣機(jī)的機(jī)械能轉(zhuǎn)化為氣體的內(nèi)能，葉輪性能的好壞對整個壓縮機(jī)有著很大的影響。離心壓縮機(jī)內(nèi)部氣流流動相當(dāng)復(fù)雜，通常是三維度的湍流流動，再加上葉片旋轉(zhuǎn)和表面曲率影響常常伴有脫流、回流及二次流的現(xiàn)象，因而使得葉片內(nèi)部氣體流動變得相當(dāng)復(fù)雜，這就使它成為流體工程中非常難的實(shí)驗(yàn)研究和數(shù)值模擬計算的問題之一[2]。葉片內(nèi)部流動的優(yōu)劣直接決定著整個級乃至整個壓縮機(jī)的性能和效率[3]。研究表明，想要提高葉片的效率、擴(kuò)大其工作范圍、提高其安全性，必需對葉片內(nèi)部流動進(jìn)行深入了解與研究。

最初的離心葉片的設(shè)計主要是幾何成型法，其中最具有代表性的是由Casey[4]提出的利用Bezier曲線、曲面來構(gòu)造葉型的方法。幾何成型方法的特點(diǎn)是簡便，容易在設(shè)計葉型考慮到簡化加工的要求，但是由于在葉片成型過程中沒有考慮葉片載荷分布對氣動性能影響，這對葉片的性能會產(chǎn)生一定的影響。1975年，美國北方工業(yè)研究工程公司(NREC)的 Jansen 在公開發(fā)表的“離心式壓縮機(jī)葉輪葉片設(shè)計”這篇文章中，首次提出了通過對葉片內(nèi)流場控制來設(shè)計扭曲葉片的方法[5]。我國于1974 年提出了利用流線曲率法的逆命題公式解決徑、混流式三元葉片扭曲葉片的設(shè)計問題的基本思想[6]，并且不斷的研究探索，逐漸的通過葉片內(nèi)全流場控制來設(shè)計葉片的“可控渦”設(shè)計方法。長期以來，離心壓縮機(jī)設(shè)計方法研究一直是葉片機(jī)械研究中的一個熱點(diǎn)和難點(diǎn)，各國研究者為設(shè)計出高性能的離心葉片而進(jìn)行了廣泛而深入的研究，并取得了一定的成果。

1葉片設(shè)計的思路與方法

在葉片內(nèi)部葉片對氣體做的功可以用歐拉方程來進(jìn)行描述：

Wth=c2uu2-c1uu1

其中c1u和c2u是進(jìn)出口處氣流的周向分速，u1和u2是進(jìn)出口處葉片的圓周速度，根據(jù)c2u與u2關(guān)系：

c2u=u2-c2rcotβ2

歐拉方程可寫為：

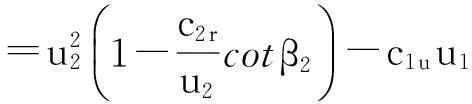
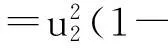
其中β2為出口氣流的氣流角，φ2r為流量系數(shù)。進(jìn)一步，如果假設(shè)葉片內(nèi)部有無數(shù)無限薄葉片，那么出口氣流角等于出口安裝角β2A，則

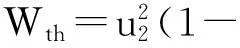
上式表明，葉片在入口條件一定的情況下c1uu1是確定的，在流量系數(shù)一定時，加功量僅與出口安裝角有關(guān)。即，在進(jìn)出口條件一定時，無論葉片形狀怎樣變化，葉片的加功量是相同的。

現(xiàn)在再回頭看歐拉方程。將葉片沿徑向n(n足夠大)等分，可以得到n+1個截面，記入口截面為0截面，出口截面為n截面，每一截面的周向分速和圓周速度分別計為ci，u和ui，相應(yīng)地，歐拉方程中的下標(biāo)1和2被分別替換為0和n。于是歐拉方程可以表示成

Wth=cn，uun-c0，uu0

=cn，uun-cn-1，uun-1+cn-1，uun-1-cn-2，uun-2+…+c1，uu1-c0，uu0

由上式可見，任意相鄰兩截面間相當(dāng)于一微元葉片，其加功量同樣由歐拉方程確定。各截面ci，uri(稱為環(huán)量)的變化情況就代表了葉片對氣流的加功工程，這就是加載規(guī)律。

上式進(jìn)一步表明，理論情況下只要進(jìn)出口條件確定，無論各截面的環(huán)量如何變化，葉片對氣流的加功量總是相同的，它們之間的差別僅僅是葉片的加載方式不同而已[7]。

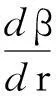
2設(shè)計實(shí)例

2.1初始參數(shù)的選定

任務(wù)參數(shù)：以空氣(理想氣體)為研究對象，設(shè)計流量6.7kg/s，進(jìn)口氣體總壓為101 325Pa，設(shè)計全壓為4 000Pa，進(jìn)口氣體總溫293.15K。

由文獻(xiàn)[1]中的方法確定葉片的基本結(jié)構(gòu)參數(shù)，其主要設(shè)計參數(shù)：

軸轉(zhuǎn)速n=1 200r/min；

葉片數(shù)Z=14；

葉片進(jìn)口半徑r1=330mm；

葉片出口半徑r2=635mm；

進(jìn)口輪盤半徑r=38.8mm；

葉片出口寬度b2=87mm；

葉片出口速度u2=79.8m/s；

葉片進(jìn)口角β1A=31.0°；

葉片出口角β2A=55.0°。

2.2葉片設(shè)計

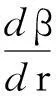
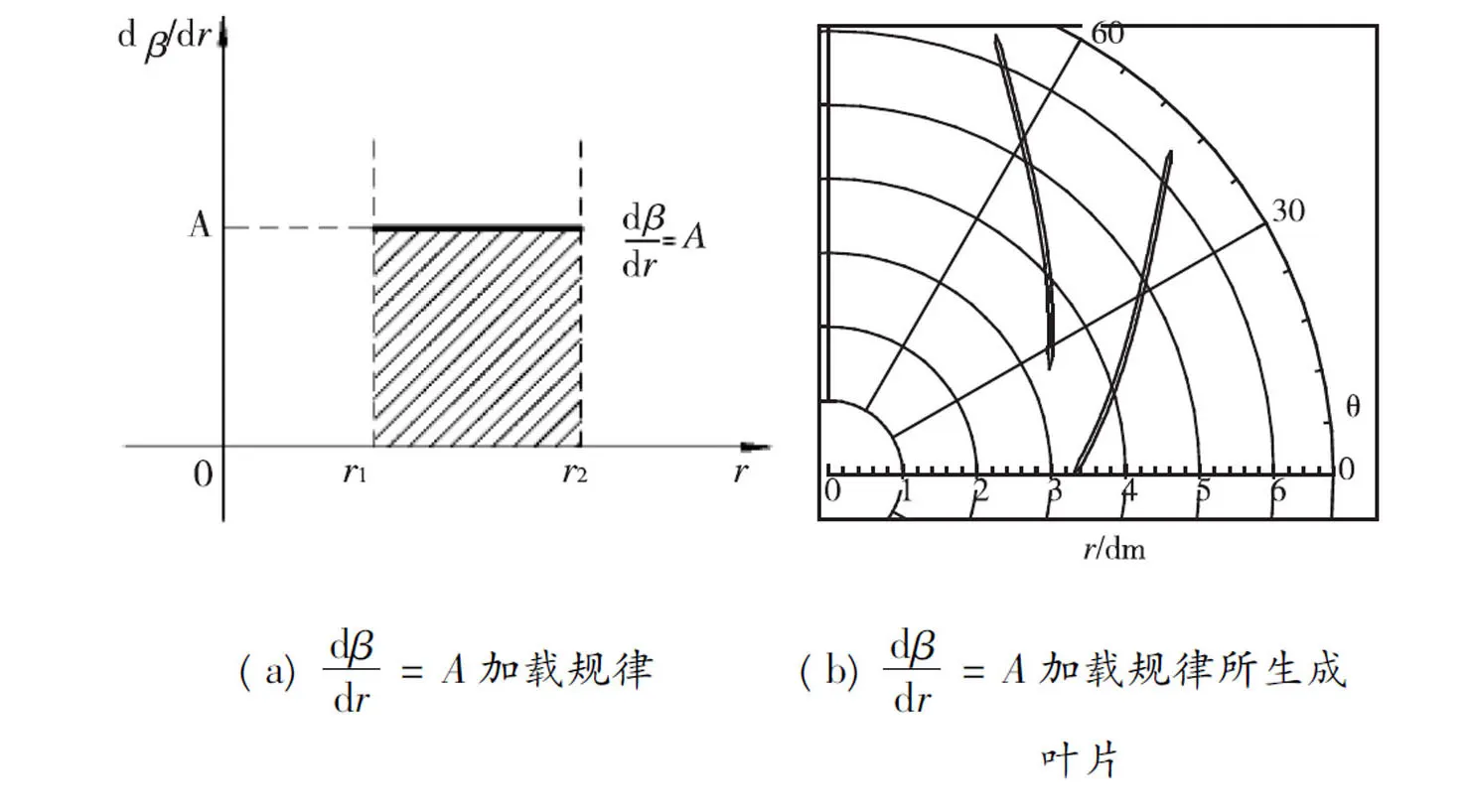
圖1

圖2

圖3

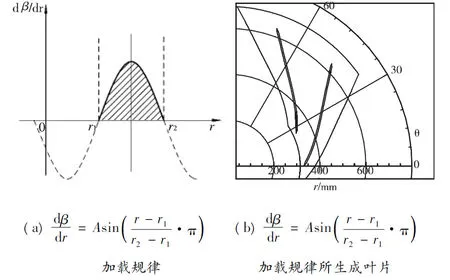
圖4

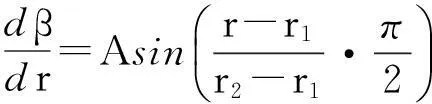
3數(shù)值計算與性能比較

3.1葉片數(shù)值模擬方法

采用CFD方法對流場進(jìn)行數(shù)值計算，湍流模型采用Spalart-Allmaras一方程模型，采用H-I型網(wǎng)格結(jié)構(gòu)，流動方向、周向的網(wǎng)格數(shù)分別為200、180[9、10]。

邊界條件：進(jìn)口給定沿徑向均勻分布的總溫、總壓和進(jìn)口氣流角。壁面采用絕熱無滑移邊界條件，給定進(jìn)口流量，調(diào)節(jié)該值可以計算不同的工況點(diǎn)。

3.2計算結(jié)果及性能比較

在設(shè)計轉(zhuǎn)速下，對4種加載規(guī)律的葉片分別進(jìn)行數(shù)值計算，可以分別得出滑移系數(shù)，壓比、效率隨流量變化的性能參數(shù)。

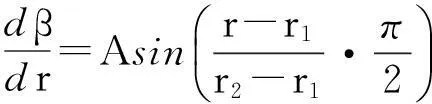
表1

不同加載規(guī)律下葉片的滑移系數(shù)比較

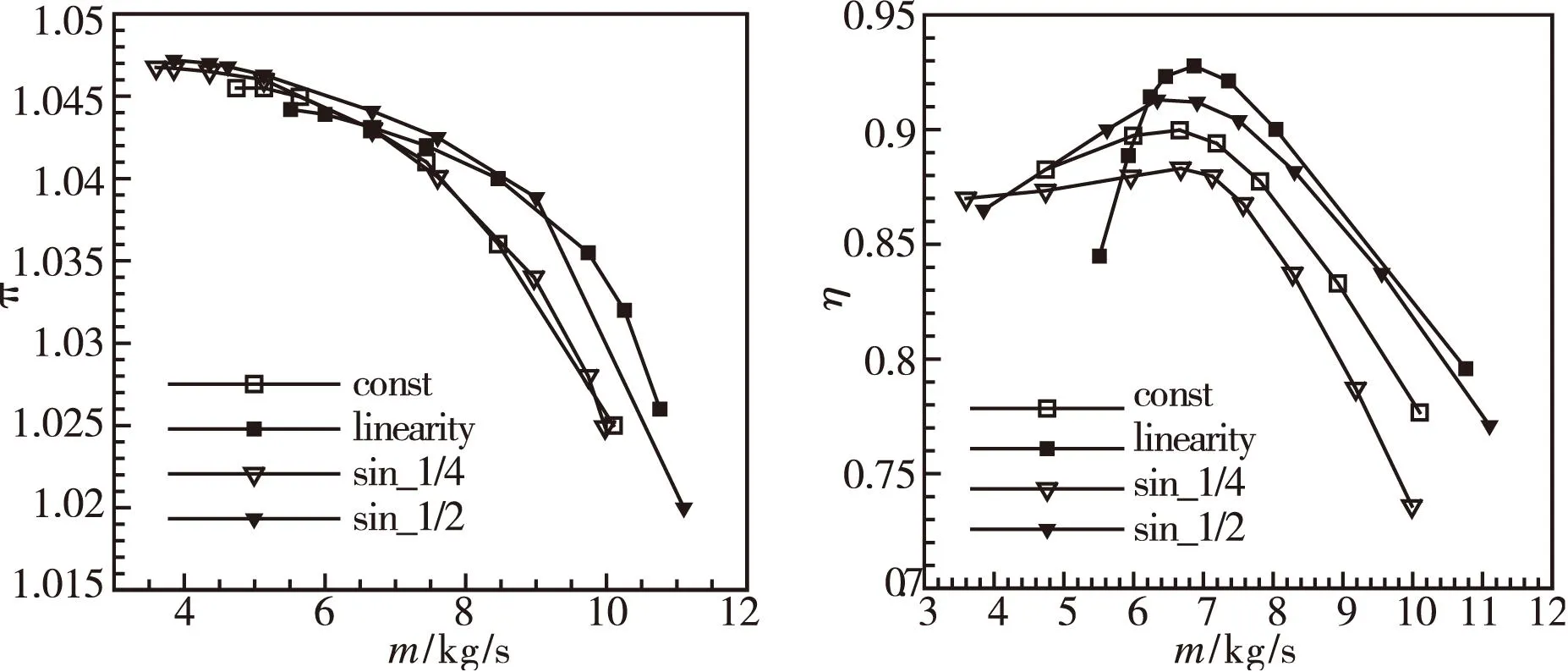
(a)總壓比流量特性曲線　　　　(b)等熵效率流量特性曲線 圖5　不同加載規(guī)律葉片性能特性曲線

由性能特性曲線圖可以看出：

1)sin_1/2加載規(guī)律所生成的的葉片阻塞流量最大，常數(shù)加載和線性加載其次，sin_1/4加載最小。

2)sin_1/4加載規(guī)律所生成的葉片的喘振流量最小，sin_1/2加載和常數(shù)加載其次，線性加載最大。

3)線性加載和sin_1/2加載式葉片的總壓比較高，sin_1/4加載和常數(shù)加載式葉片的總壓比較低。

4)線性加載規(guī)律生成的葉片效率最高，但其隨著流量減小而效率變化很大；sin_1/2加載規(guī)律式葉片比線性加載規(guī)律式葉片的效率稍低，效率變化較平穩(wěn)；sin_1/4加載規(guī)律式葉片的效率最小，隨著流量減小，效率變化平穩(wěn)。

由此，綜合阻塞流量、喘振流量、總壓比和等熵效率可以得知：所設(shè)計的四種葉片中，sin_1/2加載規(guī)律所生成的葉片性能優(yōu)于其他三種加載方式。

4結(jié)論

1)本文針對離心葉片的設(shè)計，首次提出了加載規(guī)律的參數(shù)化控制思想，采用本文設(shè)計方法來設(shè)計離心葉片是一種非常簡便和有效的設(shè)計方法，它具有物理概念清晰、幾何關(guān)系非常明確的特點(diǎn)。

2)控制加載規(guī)律的設(shè)計方法可以靈活地把葉片沿半徑方向上的加載規(guī)律設(shè)置為不同的方式，并利用β和葉片幾何尺寸的關(guān)系，可以靈活地控制葉型的扭曲和做功方式的規(guī)律。

3)通過數(shù)值計算和性能分析，驗(yàn)證了本文的設(shè)計方法可行，在所設(shè)計的四種組合加載規(guī)律中，sin_1/2加載規(guī)律所生成的葉片有較好的性能。

當(dāng)然，要找到最優(yōu)的加載規(guī)律還需要進(jìn)一步的工作，這就要求設(shè)計者有深厚的理論修養(yǎng)和長期的實(shí)驗(yàn)研究基礎(chǔ)。同時我們可以看到，利用函數(shù)和參數(shù)控制加載規(guī)律有著很強(qiáng)的適用性和廣闊的前景。

參考文獻(xiàn)

[1]王尚錦.離心壓縮機(jī)三元流動理論與應(yīng)用[M].西安:西安交通大學(xué)出版社.1991

[2]Gui F L ,Reinarts T R ,Scarnge R P. Design and experimental study of high-speed low-flow-rate centrifugal compressors[R]. IECEC Paper No.CT-39, ASME 1995

[3]徐忠.離心壓縮機(jī)原理[J].北京:機(jī)械工業(yè)出版社, 1998

[4]Casey M V. A computational geometry for the blades and internal flow channels of centrifugal compressors.Transaction of ASME, Journal of Engineering for Power, APRIL 1983, VOL. 105, 288-295

[5]Jansen W and Kirschner A M. Impeller design method for centrifugal compressor.NASA SP304, 1975

[6]苗永淼，王尚錦. 徑、混流式三元葉輪“全可控渦”設(shè)計理論和方法.工程熱物理學(xué)報(第二期)，1981年5月

[7]秦玉兵.控制加載規(guī)律下的離心壓縮機(jī)葉輪設(shè)計方法及數(shù)值計算[J].沈陽:風(fēng)機(jī)技術(shù),2007

[8]田曉平.基于控制加載規(guī)律的離心葉輪設(shè)計方法研究[J].西安:西北工業(yè)大學(xué)出版社, 2011

[9]John D. Anderson, Computation Fluid Dynamics [M]. Beijing: Machine industry press, 2007

[10]張朝輝.ANSYS 8.0結(jié)構(gòu)分析及實(shí)例解析[M].北京：機(jī)械工業(yè)出版社，2005