含氣空泡出水過程數值模擬研究

第一作者尤天慶男，工程師，1984年生

通信作者魏海鵬男，高級工程師，1982年生

含氣空泡出水過程數值模擬研究

尤天慶,張耐民,魏海鵬,程少華,趙振軍

(北京宇航系統工程研究所，北京100076)

摘要：含氣空泡在出水過程中會發生潰滅，形成較為復雜且劇烈變化的流場。首先基于含氣理想球形空泡潰滅模型，理論上分析了空泡潰滅特性，而后基于均質多相流模型，對航行體出水過程中含氣空泡潰滅現象進行了數值模擬分析。計算分析表明，含氣空泡潰滅過程存在回彈現象，會在航行體表面形成沖擊載荷，空泡內壓提高使空泡尺度增大并且可在一定程度上減小空泡內外壓差，緩解由空泡周圍流體強烈拍擊航行體壁面而產生的壓力激勵。

關鍵詞：空泡；出水；多相流；水下航行體

基金項目：國防基礎科研計劃(A0320110015)

收稿日期：2014-05-20修改稿收到日期：2014-12-05

中圖分類號:U661.1文獻標志碼：A

Numerical simulation on water exit of air-involved cavity

YOUTian-qing,ZHANGNai-min,WEIHai-peng,CHENGShao-hua,ZHAOZhen-jun(Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China)

Abstract:The cavity mixed with air will collapse during water exit, which leads to a dramatic change of flow field. The cavity collapse property was analyzed by using a spherical air-involved bubble model. Then, based on the homogenous multiphase flow model, the numerical simulation of the cavity collapse filled with air was conducted. The result shows that the rebound phenomenon will occur in the cavity water exit collapse process, and cause strong impact on vehicle surface. The analysis also presents that the rising of cavity’s inside pressure causes the growing of cavity size and reduces the inside and outside pressure difference, which eases the water impact.

Key words:cavity; water exit; multiphase flow; underwater vehicle

航行體在水下高速運動時，當流場中壓力下降至飽和蒸汽壓力以下,并維持一定時間后，空泡將產生。此時空泡為水汽化而成的水蒸汽所填充，稱之為自然空泡，一般發生在航行體頭部曲率變化較大的部位。空化為一種十分廣泛的現象，不一定局限于含汽型空穴，空泡也可以為不可凝結氣體所填充[1]，即航行體附近流場低壓區由發射過程產生的氣體或者自身排除的氣體所填充，形成含氣空泡。

在出水過程中，如果存在空泡附著在航行體表面，空泡在出水過程中會發生潰滅，產生較大擾動，對整個出水過程產生很大影響[2-4]。針對空泡的潰滅過程，眾多研究主要集中于孤立空泡的潰滅[5-7]。隨著計算流體力學和計算機技術的發展，數值求解空泡多相流場取得了一定的發展，形成了可用于模擬出水過程空泡多相流場演化的數值方法[8-9]。然而，出水空泡流場演化涉及非定常、可壓縮以及自由液面等諸多因素影響，流動機理復雜，許多問題仍然有待進一步研究。

與自然空泡不同，含氣空泡內部會存在一定量的非可凝結的空氣，與自然空化形成的水蒸汽相比，在環境壓力升高的條件下不易凝結或溶解于水中。本文首先基于理想球形空泡潰滅模型，理論上分析了含氣空泡的潰滅特性。然后采用均質多相流模型及空化模型，對理論分析所得的結果進行了深入研究。對出水空泡的潰滅過程進行了數值計算，分析了泡內氣體對出水過程流場的影響，而后開展了泡內壓力對出水過程流場特性影響分析。

1含氣空泡潰滅過程分析

假設理想球形空泡在潰滅過程中，其內部只含有非可凝結氣體而不含有水蒸汽，所含氣體質量在潰滅過程中保持不變，并且忽略表面張力的影響。空泡潰滅的初始條件是：泡內充滿壓力為pg0的理想氣體；泡外水體中無限遠處的壓力為p∞；泡內氣體的壓縮過程為絕熱過程。根據能量守恒，可得空泡潰滅過程中壁面速度表達式：

(1)

(2)

對式(1)求導可得：

(3)

由式(3)可求得，理想球形空泡潰滅過程的空泡壁面位移及速度的變化曲線(見圖1)。

由式(3)可得不同泡內壓力下的空泡壁面運動速度曲線(見圖2)。隨著空泡潰滅初始狀態泡內壓力的升高，空泡壁面運動速度逐漸減小。如此可以推斷含氣空泡出水潰滅過程中，空泡壁面水體拍擊固壁表面時所產生的沖擊壓力也將有一定程度的減弱。

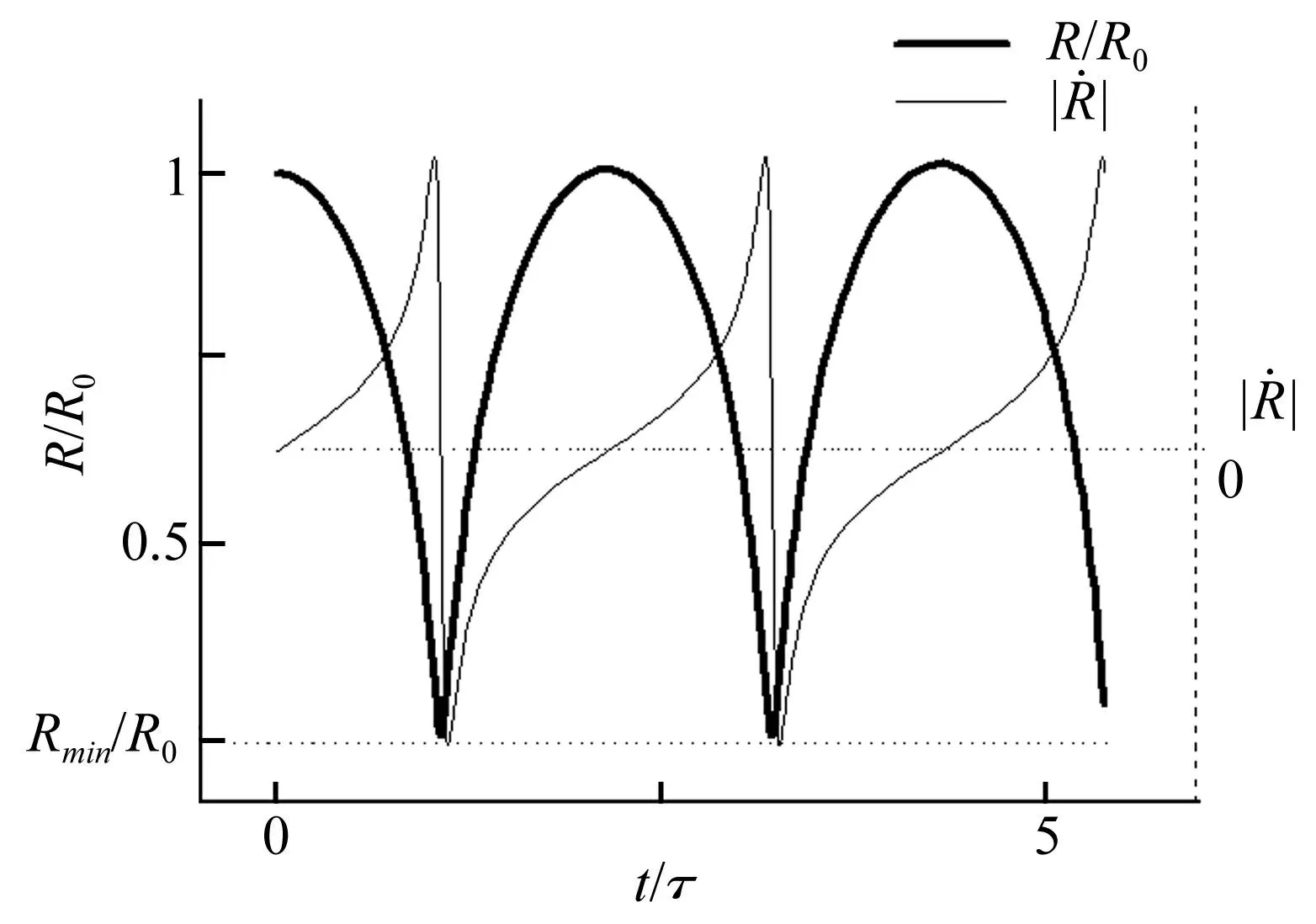
圖1　內部為非可凝結氣體的空泡壁面運動位置及速度曲線 Fig.1 Curves of cavity wall position and velocity within non-condensable gas

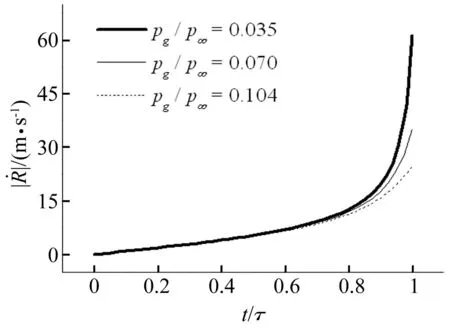
圖2　不同泡內壓力下空泡壁面運動速度曲線 Fig.2 Curves of cavity wall velocity with differentinternal pressure

2數值計算方法

采用的均質多相流模型控制方程包括雷諾平均N-S方程的守恒形式，k-ε湍流模型和流體體積分數的輸運方程。

連續性方程，動量方程，湍流模型及空化模型如下所述。

質量守恒方程：

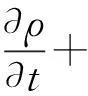
(4)

動量守恒方程：

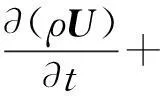
-p+B+·(μeff(U+(U)T))

(5)

標準k-ε湍流模型：

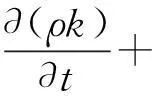
(6)

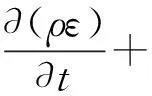
(7)

空化考慮為水與水蒸氣之間的質量轉換，其輸運方程為：

(8)

式中：Si為廣義源項；Γi為進入i相的單位體積質量源，且滿足關系式(2)。

(9)

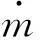
由Rayleigh-Plesset方程可導出空泡與水之間的相變表達式，

式中：pv為水的飽和蒸汽壓；rnuc為成核位置的體積率；F為經驗常數。

3數值計算結果分析

3.1含氣空泡出水過程的回彈現象

由理想球形空泡潰滅過程分析表明，空泡內的氣體會使空泡潰滅存在回彈現象。為驗證出水空泡潰滅同樣存在上述現象，計算了空泡內含有空氣的出水過程流場。這一過程流場各相分布云圖變化見圖3。圖3中vtd-1為特征時刻的無量綱表達式，t為特征時刻，初始時刻為航行頂部最高點與未受擾動自由液面相平時刻，v為航行體運動速度，d為航行體特征尺寸。在航行體頭部穿過水面過程中，附著在航行體肩部的空泡，在自由液面作用下，開始收縮并最終潰滅，含空氣空泡的潰滅過程存在空泡的回彈現象。vtd-1=1.289時，空泡收縮潰滅至最小體積。此后空泡開始逐漸回彈，vtd-1=1.647時空泡體積達峰值。此后又開始逐漸收縮至最小(vtd-1=2.047)，而后又開始回彈。

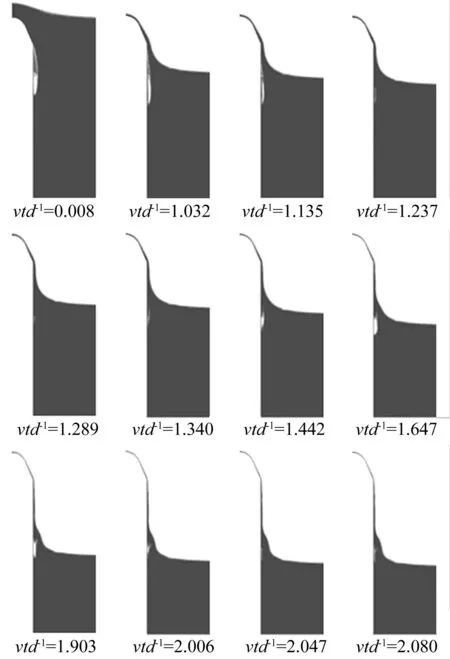
圖3　空泡中混有空氣的出水過程自由液面及空泡形態 Fig.3 Profile of free surface and cavity while air is involved in the cavity

這種出水空泡潰滅與回彈現象，與以往對處于靜水中孤立空泡潰滅的研究一致。空泡生命周期一般包括有回彈再生的階段。在水洞實驗中，這種回彈能經常觀察到。然而，實驗中也曾觀察到不回彈的空泡。例如哈里遜[10]在文丘里管嘴的實驗中發現由微不可見的氣核所形成的空泡，潰滅后未見明顯的回彈。在實驗中采用特殊的技術，可以獲得由火花產生的空泡，泡內僅含微不可計的空氣，潰滅時未見顯著的回彈。特殊技術包括將電極完全浸濕并使所有的游離氣體在壓力下溶解。反之，含有一定數量空氣的火花誘發的空泡，則顯示回彈現象。

為更清楚地表明空泡潰滅過程中航行體壁面壓力的變化情況，繪制了兩種情況沿航行體軸線方向的壓力系數隨時間變化的曲面見圖4。圖4中，Cp為壓力系數，zd-1為所描述點位置的無量綱參數，z為所描述點與航行體頂點的軸向距離。由于考慮空泡內部混有空氣的出水過程存在空泡潰滅回彈及再次潰滅的現象，空泡周圍流體再次碰撞航行體壁面，致使航行體表面壓力先后出現兩次峰值。

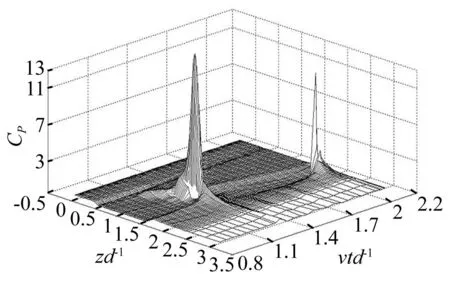
圖4　空泡中混有空氣的出水過程航行體表面壓力系數變化 Fig. 4 The vehicle surface pressure coefficient change while air is involved in the cavity

3.2空泡內壓力特性對出水過程流場的影響

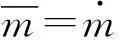
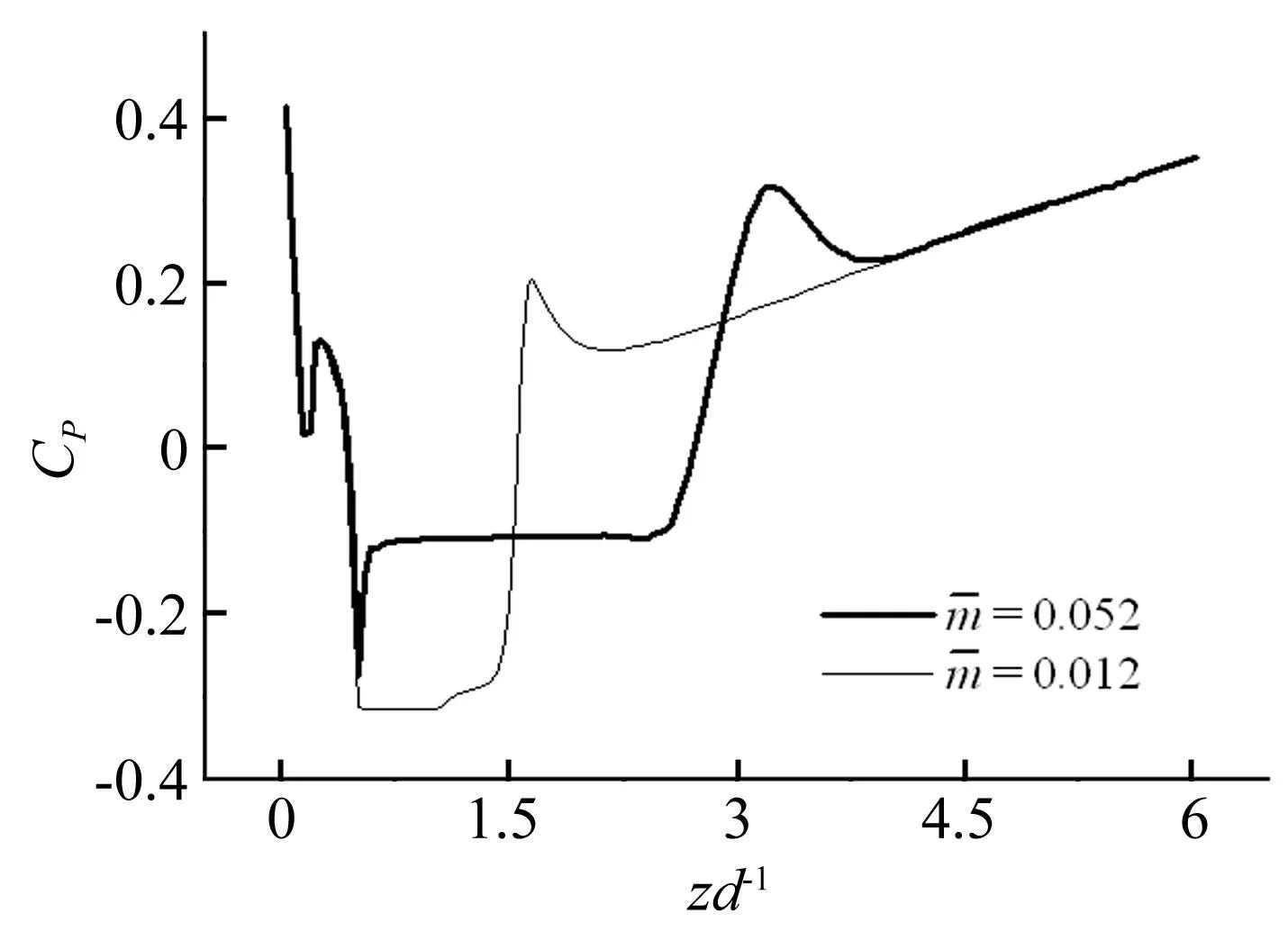
圖5　不同通氣率出水空泡初始時刻表面壓力系數分布 Fig.5 Initial pressure distribution during water exit with differentveltilation rate

3.2.1低泡壓出水過程

由于通氣率較小，在航行體頭部觸水時刻，空泡大小及泡內壓力均增長有限。隨著出水的進行，空泡逐漸被拉長，并最終斷裂。其斷裂上部分形成了體積較小的通氣空泡。隨著通氣進行，其內部壓力逐漸升高，不會出現周圍液體拍擊航行體表面的情況。其斷裂的下部分形成了混有低壓空氣的氣泡，在其周圍的液體會在壓力梯度的作用下涌向空泡內部。空泡周圍的流體以較大的速度拍擊航行體壁面，并瞬時產生較高的壓力。

圖6　低壓空泡出水過程壓力云圖 /Pa Fig.6 Contour of water exit pressure with low initial pressure /Pa

3.2.2高泡壓出水過程

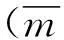
vtd-1=2.057時，通氣空泡在自由表面作用下開始斷裂，當vtd-1=2.569時，斷裂后上部分通氣空泡在持續通氣作用下，內部壓力逐漸升高，最終與外界空氣壓力持平。且空泡壁面附近流體在重力作用下逐漸下落，包裹上部空泡的流體逐漸減少。這逐漸導致上部通氣空泡破裂與周圍大氣連通。

對比vtd-1=2.057時和vtd-1=2.569時的壓力云圖，斷裂后的下部分空泡在內外壓差的作用下略有縮小。由于空泡內部為空氣，受壓縮后內部壓力略有升高。泡內壓力的升高消除了空泡內外的壓力差，空泡收縮過程進一步減緩，泡內壓力進一步增加，如vtd-1=3.081時的壓力云圖所示。隨著泡內壓力的增加以及空泡附近流體在重力作用下逐漸下落，下部分空泡開始與大氣連通，如vtd-1=3.593時的壓力云圖和空泡-自由液面輪廓線所示。

圖7　高壓空泡出水過程壓力云圖 / Pa Fig.7 Contour of water exit pressure with high initial pressure / Pa

對比高低壓兩種情況的通氣空泡出水過程，可見通氣率可明顯影響出水過程之初的空泡泡內壓力空泡大小等參數。由理想球形空泡潰滅過程分析可知，隨著泡內壓力的提升和空泡尺度的增加，空泡潰滅時刻延后，潰滅壓力峰值降低，數值計算結果明顯體現了這一規律。

針對出水過程空泡斷裂時刻，高壓空泡內外壓力差較小，空泡收縮過程較低壓空泡緩慢。在低壓空泡情況下，vtd-1=1.173時，通氣空泡斷裂為上下兩部分，在高壓空泡情況下，vtd-1=2.057時，通氣空泡在自由表面作用下開始斷裂。高壓空泡斷裂位置處空泡壁附近流體沿航行體徑向拍擊壁面無量綱速度為vc/v=0.09，明顯低于低壓空泡vc/v=0.16。因此，高壓空泡斷裂所形成的壓力脈沖Cp=0.08明顯低于低壓狀態Cp=0.26(見圖8)，這與理想球形空泡分析結果相符合。針對出水過程空泡斷裂后形成的下部分空泡，高通氣量下泡壓較高，空泡收縮過程較緩慢，消除低壓泡狀態下vtd-1=1.368時刻的兆帕量級空泡潰滅壓力脈沖。

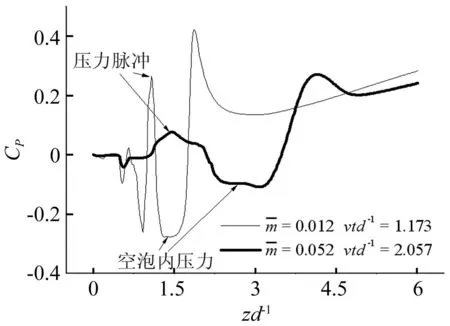
圖8　空泡斷裂時刻表面壓力系數分布 Fig.8 Pressure distribution while cavity splits

4結論

本文在考慮空泡內氣體非可凝結性和可壓縮性的情況下，分別采用理論和數值計算的方法分析了出水空泡流場演化特性，得到以下結論：

(1)基于理想球形空泡潰滅模型，考慮空泡內部氣體為非凝結理想氣體，理論上分析了通氣空泡的潰滅特性。分析結果表明，含氣空泡在潰滅過程中泡內氣體被壓縮壓力急劇升高以致產生回彈現象。通過改變空泡初始時刻的泡內壓力，得到了泡內初始壓力對空泡潰滅速度的影響。泡內氣體壓力越高潰滅速度越緩慢，潰滅至最小體積的時刻越延后。

(2)基于均質平衡流模型和空化模型，在考慮空泡內部氣體可壓縮性的情況下，分析了內部混有空氣的肩空泡出水過程流場特性，結果表明，由于肩空泡內含有非可凝結氣體，其在出水潰滅過程中會存在回彈現象，以致形成多次脈沖壓力作用于航行體表面。

(3)在考慮通入氣體可壓縮性的情況下，采用數值模擬的方法研究了泡內壓力特性對含氣空泡出水過程流場特性的影響，分析了出水過程持續通氣的空泡流場，結果表明較高的泡內初始壓力有助于緩解由空泡周圍流體強烈拍擊航行體壁面而產生的壓力激勵變化。

參考文獻

[1]Knapp R T, Daily J W, Hammitt F G. Cavitation[M]. Mcgraw-Hill book company, 1970: 63-139.

[2]Waugh J G, Stubstad G W. Water-exit behavior of missiles part 1. preliminary studies[R] Underwater Ordance Department, China Lake, California, 1961.

[3]權曉波，李巖，魏海鵬,等. 航行體出水過程空泡潰滅特性研究[J]. 船舶力學,2008,4(12):545-549.

QUAN Xiao-bo, LI Yan, WEI Hai-peng,et al. Cavitation collapse characteristic research in the out-of water progress of underwater vehicles[J].Journal of Ship Mechanics, 2008,4(12):545-549.

[4]Christopher E B. Cavitation and Bubble Dynamics[M]. Oxford:Oxford University Press.

[5]Williams P R, Williams P M, Brown S W J. A study of liquid jets formed by bubble collapse under shock waves in elastic and Newtonian liquids[J]. Journal of Non-Newtonian Fluid Mechanics, 1998, 76(1/2/3): 307-325.

[6]Zhang A M, Yao X L, Feng L H. The dynamic behavior of a gas bubble near a wall[J]. Ocean Engineering,2009, 36: 295-305.

[7]Luo Jing, Li Jian. Two-dimensional simulation of the collapse of vapor bubbles near a wall[J]. Journal of Fluids Engineering,2008, 130: 091301-1.

[8]Liu Zhi-yong, Yi Shu-qun, Yan Kai. Numerical simulation of water-exit cavity[C]//Fifth International Symposium on Cavitation, Osaka, Japan, 2003: CAV03-0S-7-018.

[9]王一偉, 黃晨光, 杜特專, 等. 航行體有攻角出水全過程數值模擬[J]. 水動力學研究與進展, 2011, 26: 48-57.

WANG Yi-wei, HUANG Chen-guang,DU Te-zhuan, et al. Numerical simulation of a submerged body exiting from water with an attack angle[J].Chinese Journal of Hydrodynamics, 2011,26:48-57.

[10]Harrison M. An experimental study of single bubble cavitation noise[J]. The Journal of the Acoustical Society of America, 1952, 24(6): 776-782.