車輛系統的多個蛇行運動

高學軍，李映輝, 關慶華

(1. 成都理工大學地質災害防治與地質環境保護國家重點實驗室, 成都　610059;2.西南交通大學力學與工程學院, 成都　610031; 3. 西南交通大學牽引動力國家重點實驗室, 成都　610031)

第一作者高學軍男，博士, 副教授，1979年生

車輛系統的多個蛇行運動

高學軍1，李映輝2, 關慶華3

(1. 成都理工大學地質災害防治與地質環境保護國家重點實驗室, 成都610059;2.西南交通大學力學與工程學院, 成都610031; 3. 西南交通大學牽引動力國家重點實驗室, 成都610031)

摘要：采用升速法和降速法對復雜非線性輪軌接觸關系下車輛系統的分岔行為進行研究，發現系統存在運動幅值相差不大的兩個蛇行運動解并存的現象，這種多個蛇行運動解并存的特性與一般的由單個亞臨界Hopf分岔所引起的穩定定常運動與穩定蛇行運動并存的特性有所不同，很容易使車輛在相應速度附近運行時由于擾動的不同而使擺振幅值往復變化，影響車輛的正常安全運行，因此臨界速度測定時需要在多種可能的激勵條件下多次測試綜合分析。

關鍵詞：輪軌接觸關系; 車輛系統; 分岔; 并存; 臨界速度

基金項目：國家自然科學基金項目(11102030, 11372257, 51305360,11472064)

收稿日期：2014-01-02修改稿收到日期：2014-05-08

中圖分類號:O322;U260.11

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.11.035

Abstract:The bifurcation behaviors of a railway vehicle system with a complex nonlinear wheel-rail contact relation were investigated using the methods of increasing speed and decreasing speed. It was shown that two hunting motions with similar amplitudes coexist in the system; there are some differences between the coexistence of multiple hunting motions and the coexistence of the stable steady motions and the stable hunting motions caused by a single sub-critical Hopf bifurcation in the railway vehicle system; the coexistence of multiple hunting motions may easily cause the reciprocating change of the vehicle’s shimmy amplitude due to different disturbances to affect the normal and safe operation of the vehicle; therefore, the critical speed should be determined through comprehensive analysis under various kinds of possible excitations and multiple tests.

Multiple hunting motions of a railway vehicle system

GAOXue-jun1,LIYing-hui2,GUANQing-hua3(1. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China;2. School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China;3. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

Key words:wheel-rail contact relation; railway vehicle system; bifurcation; coexistence; critical speed

車輛系統橫向運動穩定性研究[1-2]一直是鐵路工程師和科研工作者非常關心的問題，因為它不但涉及到車輛臨界速度[3-4]的確定，直接影響列車允許的最高運行速度，而且還涉及到車輛運行過程中各種可能的運動狀態及其對其它性能指標的影響。在這方面，國內外許多專家學者已開展了卓有成效的研究工作：Cooperrider等[5]應用非線性修正的縱向和橫向蠕滑力(未考慮自旋蠕滑力)研究車輛系統的動力學行為。True[6]發現對稱的車輛系統中會存在不對稱的運動形式。楊紹普等[7]對具有滯后非線性懸掛的轉向架和車輛蛇行運動的穩定進行了研究。高學軍等[8]探討了延續算法在簡單軌道客車系統分岔方面的應用。這些研究主要是采用線性或簡單非線性輪軌接觸關系來分析的，與實際的輪軌接觸狀態存在一些差別，使得應用的范圍受到部分限制。

已有學者開始應用復雜非線性輪軌接觸關系來進行分析。Zeng[9]使用QR算法結合牛頓-拉夫遜法求解車輛系統的Hopf分岔點，應用龍格-庫塔法結合Poincaré映射確定系統的極限環。Xia[10]考慮了楔塊的二維干摩擦特性研究了三大件式貨車的動力學問題。Hoffmann[11]通過引入“事件系統”分析了歐洲兩軸貨車的動力學問題。Gao等[12]則研究了真實的輪軌型面下轉向架系統的對稱/不對稱分岔行為。

在前人研究工作的基礎上，本文擬采用復雜非線性輪軌接觸關系分析鐵道車輛系統的分岔行為，主要討論分岔過程中存在的多個蛇行運動的情形。研究結果可為進一步改善車輛運行品質、臨界速度的測定及許用范圍值的確定提供參考和部分依據。

1動力學模型描述

1.1復雜非線性輪軌接觸關系

對中國的車輪踏面LM和鋼軌型面CHN60，標準軌距1 435 mm，輪對內側距1 353 mm，采用RSGEO[13]軟件包即可生成輪軌相互匹配時的復雜非線性輪軌接觸關系數表。

圖1給出了輪軌接觸數表中Kalker系數C11與輪對橫移量之間的非線性變化關系。由圖可見，當輪對橫移量較小時，Kalker系數C11與輪對橫移量之間存在近似的線性關系，而一旦輪對橫移量超過某一值時，C11與輪對橫移量之間則不再是簡單的線性關系，而是隨著輪對橫移量的變化急劇變化，其中不乏突增或突減的區域。

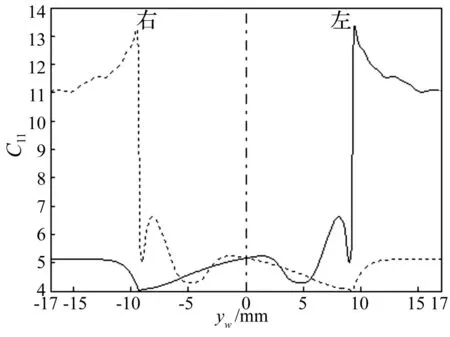
圖1　Kalker系數C11與輪對橫移量之間的非線性變化關系Fig.1 The Kalker’s creepage coefficients C11 as a nonlinear function of the lateral displacement of the wheel-set

1.2蠕滑力/力矩的計算

輪軌間的蠕滑力/力矩與蠕滑率有關，縱向、橫向、自旋蠕滑率對左輪(l,±或?取上面的符號，后同)，右輪(r, ±或?取下面的符號，后同)可依次表示為[14]

(1)

式中:V為車輛運行速度；Ω=V/r0為車輪名義滾動角速度；yw為輪對橫向位移；ψw為輪對搖頭角位移；r(l, r)為左/右輪滾動圓半徑；(δl,δr)為左/右輪輪軌接觸角；φw為輪對側滾角；(al,ar)為輪對質心到左/右輪接觸點的橫向距離。

先根據Kalker線性蠕滑理論[15]計算輪軌間的線性蠕滑力，然后再應用沈氏蠕滑理論[16]進行非線性修正，最后將修正后的接觸斑蠕滑力/力矩通過坐標變換轉換到軌道坐標系內即可建立車輛系統的運動微分方程組。

1.3法向接觸力的計算

實際上，車輛運行中的法向力也是隨著輪對橫移量的不同在不斷發生著變化。

圖2給出了由RSGEO得到并轉換后的靜態法向力與輪對橫移量的非線性變化關系，由圖2可知，大多數情況下，靜態法向力與軸載荷的一半相差不大，只有當輪對橫移量超過輪軌間隙(η=9.0 mm)時，法向力才會發生急劇變化而減小。

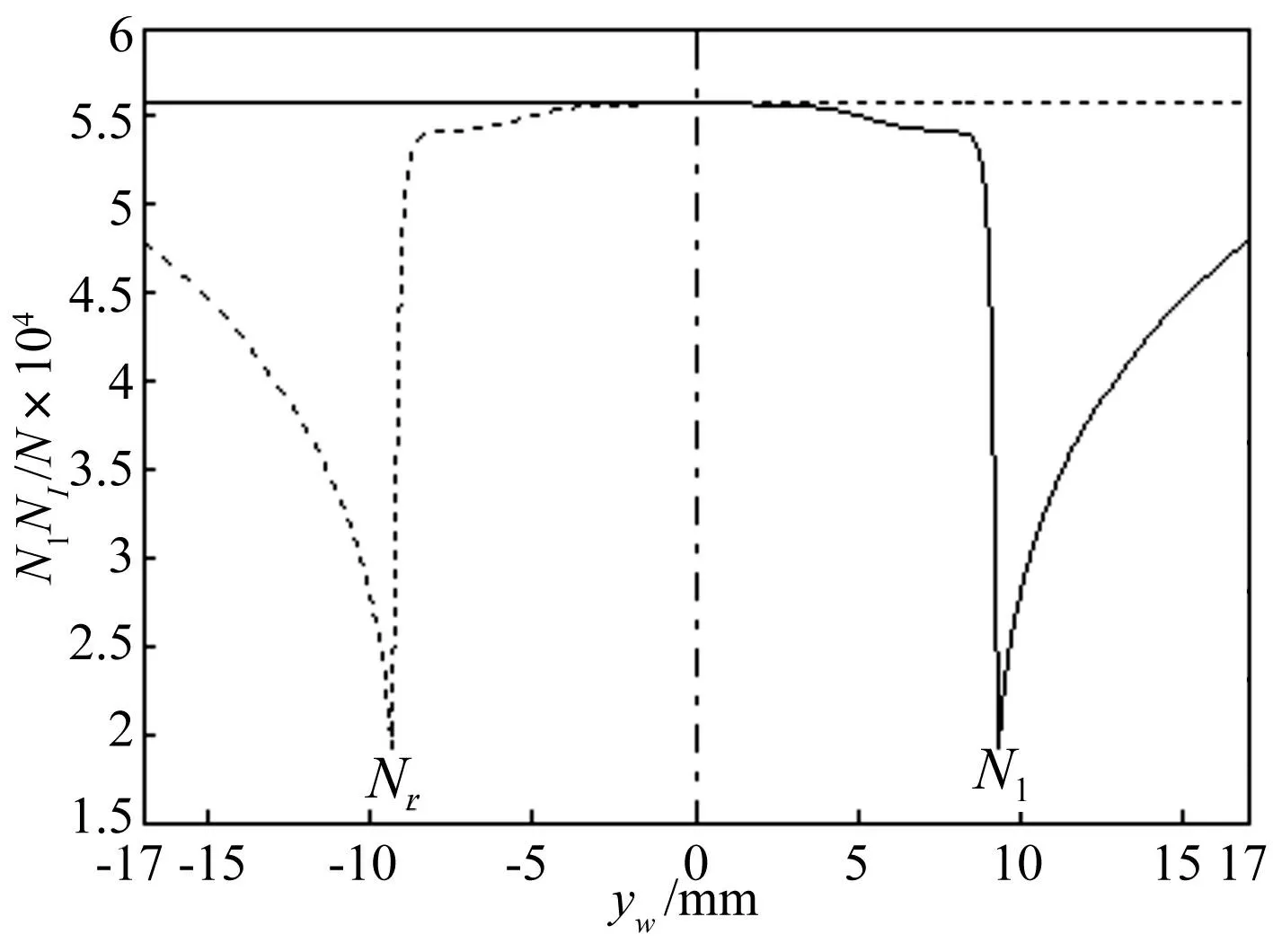
圖2　靜態法向力與輪對橫移量的非線性變化關系Fig.2 The static normal forces as a nonlinear function of the lateral displacement of the wheel-set

左、右輪法向力在橫向方向的分量N(l,r)y和垂向方向的分量N(l,r)z分別為：

(2)

1.4車輛系統運動微分方程

考慮包括1個車體(mc,Icx,Icz)、2個構架(mt,Itx,Itz)、4個輪對(mw,Iwx,Iwz)等剛體和一系懸掛(Kpx,Kpy,Kpz,Cpx,Cpy,Cpz)及二系懸掛(Ksx,Ksy,Ksz,Csx,Csy,Csz)的四軸客車橫向穩定性分析模型(見圖3)。

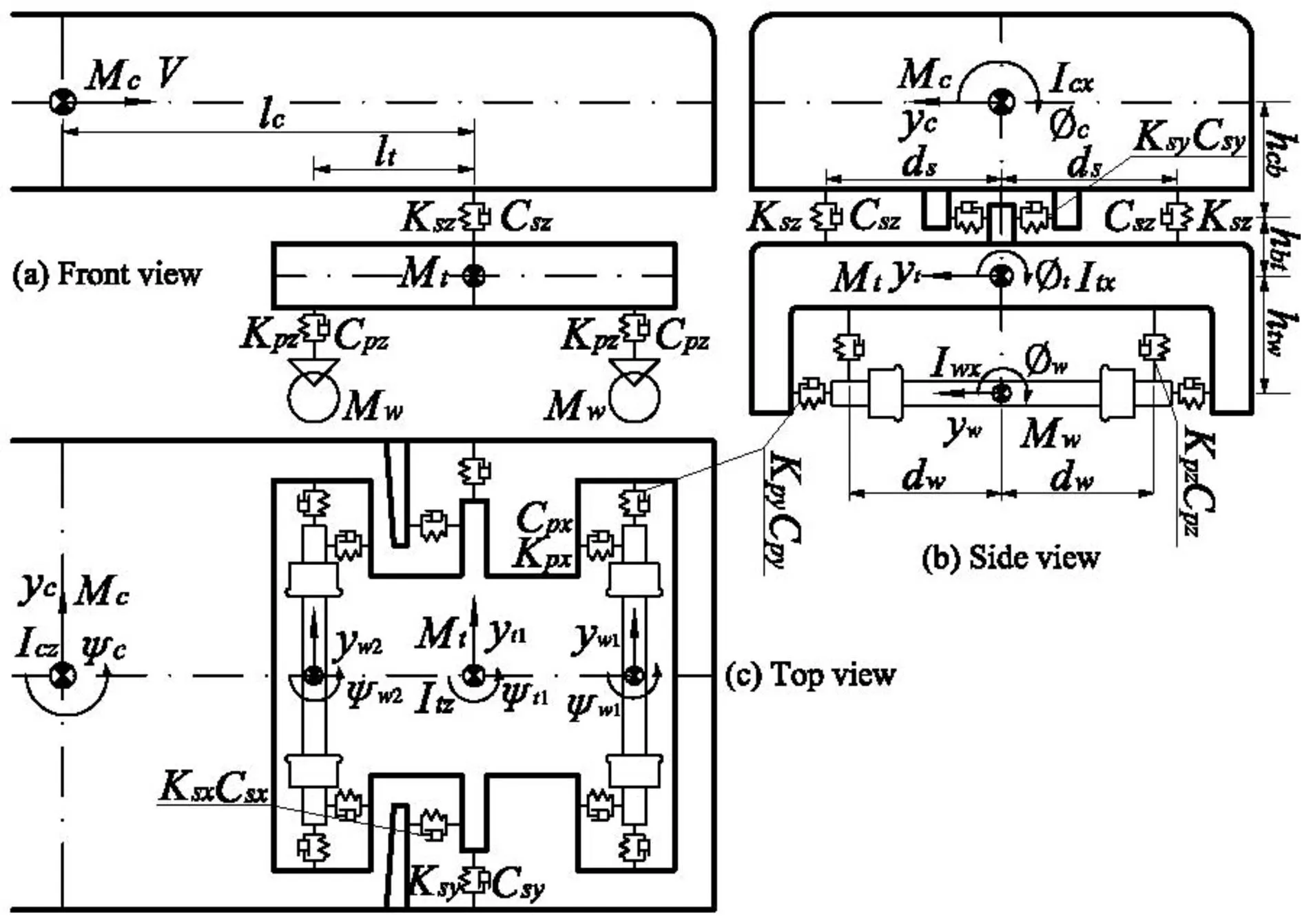
圖3　四軸客車橫向穩定性分析模型Fig.3 Model of four-axle railway passenger car system

分析中只考慮各個剛體的橫向運動[2]，因此整個系統共有17個自由度：4個輪對的橫移ywi(i=1-4)和搖頭ψwi運動；2個構架的橫移ytj(j=1-2)、側滾φtj及搖頭ψtj運動；車體的橫移yc，側滾φc及搖頭ψc運動。

整個車輛系統運動微分方程組可以表示如下

(3)

式中:F(l,r)x、F(l,r)y、M(l,r)z為非線性關系修正且已轉換到軌道坐標系內的縱向蠕滑力、橫向蠕滑力和旋轉蠕滑力矩。dw為一系懸掛橫向距離之半，ds為二系懸掛橫向距離之半，lt是轉向架軸距之半，lc為車輛定距之半。hcb為車體重心至二系懸掛高度，hbt為構架重心至二系懸掛高度，htw為構架重心至一系懸掛高度。

式(3)中一系懸掛縱向力、橫向力、垂向力為

(4)

式中:i=1,3時，±或?取上面的符號；i=2,4時則取下面的符號。下標i(j)=1(1), 2(1), 3(2), 4(2)代表四個輪對及其所對應的轉向架。

同理，二系懸掛縱向力、橫向力、垂向力為

(5)

式中:j=1,2分別為前后轉向架構架且當j=1時，±或?取上面的符號；j=2時則取下面的符號。

令系統狀態向量y∈R34，則車輛系統的動力學問題式(3)可歸結為如下形式的自治常微分方程組系統

(6)

式中:V∈R+是系統參數，此處即為車輛運行速度，f為狀態向量函數。

2分析方法

首先通過解析法并結合數值方法確定系統式(6)的線性化Jacobi矩陣，求解系統的Hopf分岔點速度。然后通過Poincaré截面法構造分岔圖說明系統的分岔行為。分析中將Poincaré截面定義為前轉向架前導輪對橫向速度為零，橫向位移非負的那個瞬時

(7)

在接觸數表的使用方面，采用三次樣條對任意輪對橫移處的相關非線性輪軌接觸相關參量進行插值，以保證計算結果的可靠性。

3數值計算結果與分析

以某高速客車為分析對象，車輛系統中各剛體的質量值、剛度系數、阻尼系數等，輪軌間的粘著系數取μ=0.40。

3.1Hopf分岔點

為了尋求車輛系統的Hopf分岔點，需要通過方程組式(6)線性化系統Jacobi矩陣的特征值進行判定。圖4給出的是系統Jacobi矩陣非零元素分布情況。其中“*”表示解析計算元素，“+”表示數值計算元素，“1”表示1元素。雖然整個矩陣共有34×34=1156個元素，但非零元素卻只有159個，而這些元素中需要通過數值計算的則只有32個，應用這種方法可以大大提高計算的效率和精度。

圖4　Jacobi矩陣非零元素分布情況Fig.4 The distribution of the nonzero elements of the Jacobi matrix

分析中，應用向前差分法數值計算Jacobi矩陣中的數值計算元素。為了得到第i行第j列處數值計算元素的值，若函數在yj處的值為fi，現給yj增加一個擾動δ，得到該狀態下的函數值fi,+，則Jacobi矩陣(i,j)處數值計算元素的值為

(8)

計算中系統狀態向量y的初始值取蛇行運動(如速度V=67.5 m/s)時某個解向量的10-6倍，而擾動量則取δ=10-9。

通過計算發現當車輛運行速度V=97.491 m/s (α1,2=-1.004×10-5±26.405i,α代表系統特征值)時，系統第一對復共軛特征值正向穿越虛軸，原來穩定的定常解變得不穩定，據此判定V=97.491 m/s是系統第1個Hopf分岔點速度。當車輛運行速度繼續增加到V=100.816 m/s(α1,2=0.351±26.851i,α3,4=2.739×10-5± 26.871i)時，系統又有一對復共軛特征值正向穿越虛軸，原來不穩定的定常解變得“更加不穩定”，由此可以斷定V=100.816 m/s是系統第2個Hopf分岔點速度。從這兩個不同的Hopf分岔點會分岔出不同的周期解分支，下面進行闡釋。

3.2蛇行運動1解

圖5　前轉向架前導輪對橫向位移分岔圖Fig.5 The bifurcation diagram of the leading wheel-set of the front bogie showing the lateral displacements versus the speed

圖5給出的是前轉向架前導輪對(1位輪對)在速度67.0 m/s

因降速過程中出現多次跳躍現象，再通過升速的方法追蹤系統其它可能的分岔點。車輛運行速度從VA=68.5 m/s的蛇行運動解開始逐漸增加，數值積分初始值的取法與降速時類似，整個系統則會沿著ABB′CC′DD′E解分支前進。也就是說，隨著速度的增加，1位輪對橫向振動幅值緩慢增加達到圖中的B點，然后出現一個跳躍，從周期吸引子B點跳躍到周期吸引子B′點。之后隨著速度的繼續增加，振動幅值緩慢增加直到到達C點之后出現一個大幅跳躍到周期吸引子C′點上，而后到達D點之后又跳躍到更高幅值的D′點上，最后到達E點。

由上述分析可知，降速過程中的跳躍HH′比升速過程中的跳躍BB′延遲了，形成了遲滯現象。由此可以推斷，B點和H點對應于車輛系統的兩個鞍結分岔點，在BH之間應該存在不穩定的周期解分支曲線，類似的現象也同樣發生于CG和DF點之間，因此可以確定：整個分岔行為都是在同一個解分支上發生的。

為說明圖5中從A點跳躍到定常解的現象，圖6給出了相同初始條件下車輛運行速度分別為V=68.5 m/s和V=68.4 m/s時1位輪對橫向位移時間歷程圖。由圖可見，當運行速度V=68.5 m/s時，隨著時間的推移，1位輪對以8.841 4 mm的振動幅值作周期性的橫向運動；而當運行速度降低到V=68.4 m/s時，隨著時間的延續，1位輪對橫向振動最終衰減到軌道中心線的位置。

圖6　速度V=68.5 m/s和V=68.4 m/s時前轉向架前導輪對橫向位移時間歷程圖Fig.6 Time histories of the leading wheel-set of the front bogie at V=68.5 m/s and V=68.4 m/s

3.3蛇行運動2解

一個很有意思的現象是，在圖5中周期解位置的附近還存在另外一個周期解分支見圖7。當車輛運行速度V≤85.8 m/s時，該周期解分支所發生的分岔現象與圖5類似，只是相對應特征點的位置及幅值有所變化；當速度達到V=85.8 m/s時，這個解分支與圖5中的解分支合并成一個周期解分支，因此后面的分岔現象與圖5完全一致，這里就不再對這個解分支上的分岔現象及具體狀態進行重復描述。

圖7　前轉向架前導輪對橫向位移分岔圖Fig.7 The bifurcation diagram of the leading wheel-set of the front bogie showing the lateral displacements versus the speed

表2給出了蛇行運動1解和2解相關特征點值，其中灰色區域代表兩個解分支重合部分的特征點值。由表可知，蛇行運動2解和蛇行運動1解確實分屬于兩個不同的解分支。

表1　蛇行運動1解和2解相關特征點值

3.4小討論

實際上，在鐵道車輛系統中，蛇行運動是一種非常普遍的自激振橫向擺動現象，這種現象主要是由車輛的前進速度和輪軌間的非線性接觸力引起。由于這種運動是鐵道車輛系統的一種內在特性，因此車輛蛇行運動一旦出現就很難被消除，除非車輛的運行速度低于車輛臨界速度。當車輛發生蛇行運動時，試圖控制系統的擾動使蛇行運動消除基本是不可能的，因為實際的軌道不可能是理想光滑平直的，總是存在很多的不平順，這些不平順不停的“激發”車輛系統，使其響應實際上是大量瞬態成分和穩態成分疊加的結果，因此蛇行運動時實際的實驗測試結果往往看起來并不如圖6中蛇行運動的結果平整、光滑。

由于車輛臨界速度定義為在參數-解空間中尋找最高速度值使定常解是唯一漸近穩定的解，或者尋找最低速度值使蛇行運動剛好出現的過程，因此對應本文所研究的車輛系統，臨界速度應為V=67.5 m/s，Hopf分岔點速度為V=97.491 m/s和V=100.816 m/s，系統實際上發生的是亞臨界Hopf分岔，其間存在不穩定的周期解分支曲線。

需要說明的是，在模擬或實際的測試中，如果被激發起來的車輛系統恰好位于圖5解分支所確定的吸引域上，則會得出臨界速度為V=68.5 m/s的不正確結論，從這方面來說，臨界速度的測定需要在多種可能的激勵條件下多次測試綜合分析才好，而這更需要充分了解臨界速度區域車輛系統的相關動力學行為。當然，本文中這兩個點的速度相差不大，在具體的工程設計中為了安全起見還要進行折減，因此對工程設計沒有任何影響。但如果這兩個值相差較大呢？在這方面值得進一步研究探討。

4結論

本文采用升速法和降速法對復雜非線性輪軌接觸關系下車輛系統速度大范圍內的分岔行為進行了研究。發現車輛系統因發生亞臨界Hopf分岔而存在穩定的定常運動與穩定的周期運動并存的現象，同時也發現車輛系統存在運動幅值相差不大的兩個蛇行運動解并存的現象。這種現象與整個車輛系統的構造、各部件之間的相互聯結及作用、各種參數的取值(質量、慣量、剛度、阻尼、長度、距離)及輪軌接觸關系等息息相關，可以說它們的“聯合”作用導致了多個蛇行運動解的并存現象。另一方面，這種多個蛇行運動解并存的特性與一般的由單個亞臨界Hopf分岔所引起的穩定定常運動與穩定蛇行運動并存的特性有所不同，很容易使車輛在相應速度附近運行時由于擾動的不同而使擺振幅值往復變化，影響車輛的正常使用并給安全運行帶來危險隱患，因此應該盡量避免。據此說明臨界速度的測定需要在多種可能的激勵條件下多次測試綜合分析，而這更需要充分了解車輛運行速度高于臨界速度時車輛系統的相關動力學行為。

參考文獻

[1]Knothe K, Bohm F. History of stability of railway and road vehicles[J]. Vehicle System Dynamics, 1999, 31(5): 283-323.

[2]Garg V K, Dukkipati RV. 鐵道車輛系統動力學[M]. 沈利人,譯. 成都: 西南交通大學出版社, 1998.

[3]True H. On the critical speed of high-speed railway vehicles[C]. Noise and Vibration on High-Speed Railways. FEUP Porto Portugal, 2008, 149-166.

[4]翟婉明. 車輛-軌道耦合動力學[M]. 2版.北京: 中國鐵道出版社, 2002.

[5]Cooperrider N K. The hunting behavior of conventional railway trucks[J]. ASME Journal of Engineering for Industry, 1972, 94(2): 752-762.

[6]True, H. Railway vehicle chaos and asymmetric hunting[J]. Vehicle System Dynamics, 1992, 20(S1): 625-637.

[7]楊紹普, 申永軍. 滯后非線性系統的分岔與奇異性[M]. 北京: 科學出版社, 2003.

[8]高學軍, 李映輝, 樂源. 延續算法在簡單軌道客車系統分岔中的應用[J]. 振動與沖擊, 2012, 31(20): 177-182.

GAO Xue-jun, LI Ying-hui, YUE Yuan. Continuation method and its application in bifurcation of a railway passenger car system with simple rails[J]. Journal of Vibration and Shock, 2012, 31(20): 177-182.

[9]Zeng J. Numerical analysis of nonlinear stability for railway passenger cars[J]. Chinese Journal of Mechanical Engineering, 2001, 14(2): 97-101.

[10]Xia, F.J. The dynamics of the three-piece-freight truck[D]. The Technical University of Denmark, Doctor Thesis, 2002.

[11]Hoffmann M. On the dynamics of European two-axle railway freight wagons[J]. Nonlinear Dynamics, 2008, 52(4): 301-311.

[12]Gao X J, Li Y H, Yue Y, et al. Symmetric/asymmetric bifurcation behaviours of a bogie system[J]. Journal of Sound and Vibration, 2013, 332(4): 936-951.

[13]Walter K, Moelle D. ACRadSchiene-To create or approximate wheel/rail profiles[R], 2010.

[14]Petersen DE, Hoffmann M. Curving dynamics of railway vehicles[R]. Informatics and Mathematical Modelling, The Technical University of Denmark, Lyngby, 2002.

[15]Kalker J J. A fast algorithm for the simplified theory of rolling contact[J]. Vehicle System Dynamics, 1982, 11(1): 1-13.

[16]Shen ZY, Hedrick JK, Elkins JA. A comparison of alternative creep force models for rail vehicle dynamic analysis[C]. Proceeding of 8th IAVSD Symposium on Vehicle System Dynamics, Dynamics of Vehicles on Roads and Tracks. MIT, Cambridge: Swets and Zeitlinger, 1984, 591-605.