阻尼對耦合非線性能量阱系統影響研究

熊　懷，孔憲仁, 劉　源

(哈爾濱工業大學衛星技術研究所，哈爾濱　150080)

第一作者熊懷男，博士生，1989年生

阻尼對耦合非線性能量阱系統影響研究

熊懷，孔憲仁, 劉源

(哈爾濱工業大學衛星技術研究所，哈爾濱150080)

摘要：研究了耦合非線性能量阱的非保守系統的定向能量傳遞現象。基于復變量平均法推導含有阻尼參數的系統慢變方程，求解出系統能量與各參數近似關系，獲得了系統能夠實現定向能量傳遞時阻尼必須滿足的條件，并給出了非線性能量阱具有吸振能力時線性振子阻尼有效范圍，最后數值分析驗證上述研究結果。

關鍵詞：非線性能量阱；定向能量傳遞；立方剛度；阻尼約束；振動抑制

基金項目：國家自然科學基金(51375109)；哈爾濱工業大學科研創新基金(HIT. NSRIF. 2014027)

收稿日期：2013-11-08修改稿收到日期：2014-03-03

通信作者劉源男，講師，1981年生

中圖分類號:O328; O322

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.11.021

Abstract:Here, targeted energy transfer was investigated in a non-conservative system with nonlinear energy sinks. Firstly, the system slowly-varying equation containing damping parameters was derived based on the complex-averaging method. Then, the approximate relationships between the system energy and parameters were solved, the necessary conditions satisifed by damping to realize system’s targeted energy transfer were achieved. The effective range of a linear oscillator’s damping during nonlinear energy sinks having the capacity of vibration suppression was gained. At last, the above study results were verified with numerical simulations.

Influence of structural damping on a system with nonlinear energy sinks

XIONGHuai,KONGXian-ren,LIUYuan(Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150080, China)

Key words:nonlinear energy sink; targeted energy transfer; cubic stiffness; damping conditions; vibration suppression

衛星在整個生命周期中需要經歷苛刻的動力學環境，而衛星快速響應[1]、即插即用[2]等新概念新技術的引入對振動環境提出更高的要求，這對星上敏感部、組件局部振動抑制或整星隔振技術提出了新的挑戰。近年來，以定向能量傳遞(Targeted Energy Transfer，TET)為吸振機理的非線性能量阱(Nonlinear Energy Sink，NES)得到長足的發展，它有減振效率高、時間短、吸振頻帶寬和魯棒性強等特點，這為衛星減振系統設計提供了一種新的途徑。

耦合非線性振子的系統各模態之間容易發生相互作用，從而使能量在振子間相互傳遞，TET是指在一定條件下振子能量能夠實現定向、高效傳遞的特殊現象。深入分析實現TET的必要條件有助于NES的進一步研究。文獻[3-4]用非平穩變換法研究了耦合理想立方剛度的Hamilton系統的能量傳遞，首次指出在1:1內共振條件下系統能夠實現TET，并用數值方法證明在小阻尼系統中同樣存在定向能量傳遞現象。文獻[5]提出一種耦合非線性振子系統分析方法——復變量平均法，基于該法文中還指出系統各振子存在模態局部化，使得能量集中。

NES的減振效率與TET密切相關，文獻[6]中分析了NES質量比對系統能量傳遞影響，并得到NES的質量比應遠遠小于1的結論；而文獻[7]研究表明在特定初始條件下系統實現能量完全傳遞時有一個最小質量比。可見NES的質量比具有一定的范圍。而文獻[8]用復變量平均法研究理想立方剛度的NES對振動抑制效率的影響，合理的設計非線性剛度能夠極大的提升NES振動抑制效率。在文獻[9]中討論了NES振動抑制效率對初始條件的敏感依賴性，結果表明在保守系統中只有特定的初始條件范圍內NES才能實現TET。此外還有其它大量文獻(參閱文獻[10-12])關于NES的力學特性研究。

我們注意到，關于NES的研究均集中在保守的Hamilton系統前提下，小阻尼系統NES也具有吸振能力。可見，阻尼在一定程度上影響著非線性能量阱。本文將研究系統阻尼對耦合NES系統振動抑制效果影響。文中首先用復變量平均法推導出系統能量傳遞和耗散的近似關系，利用該式得出了NES阻尼對能量耗散的影響；基于非保守系統的慢變方程，得到系統能量與系統各參數關系式，基于該式得到系統實現TET阻尼的必要條件；綜上兩點結論求得NES能夠進行振動抑制時主振子阻尼的臨界值；最后數值仿真驗證上述結論。

1系統動力學模型簡介

1.1系統模型

星上某敏感部件的振動抑制模型可簡化為圖 1所示的耦合單自由度NES的線性振主結構。該結構中k2為理想的立方剛度，其它均為線性參數，該非保守系統微分方程可以表示為式(1)。

圖1　耦合NES結構簡圖Fig.1 Schematic of system coupled NES

(1)

將式(1)寫成無量綱方程

(2)

式中:

(3)

用復變量平均法對推導式(2)的慢變方程。

1.2系統慢變方程

對式(2)引入變量替換

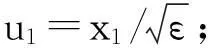
(4)

討論NES在1:1主內共振時的振動抑制效果，引入復變量

(5)

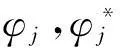
φj=φj0+εφj1;j=1,2

(6)

不難得出系統的慢變方程

(7)

(8)

式中:δ=1/ε。值得一提的是，在多尺度展開中質量比要求：ε?1，這是TET產生的必要條件，結合該慢變方程式(7)和式(8)可以對耦合NES系統阻尼進行分析。

2NES阻尼分析

耦合NES結構中的阻尼是系統能夠實現TET的前提條件，這一部分以耦合NES的非線性系統能夠發生跳躍為出發點，分析NES阻尼條件。在文獻[10]中提到在系統趨于平衡態時有

(9)

將復變量用模和相角表示，即

φj0=Rj(t1)exp[iθj(t1)]

j=1,2

(10)

將式(10)代入式(7)和式(9)，令其實部與虛部分別相等，可以得到

(11)

在耦合NES的系統中存在阻尼時，系統一定存在能量的耗散。式(11)中的第一式表示能量耗散，當阻尼均為0時，系統主結構的能量耗散率為0，顯然此時系統為對應的保守系統，并不會引起能量的減少；當系統中兩個阻尼至少有一個不為0時，式(11)第一個等式右端始終小于0，這表示能量是一直在減小的。

對于第二式有隱含關系

(12)

圖2　振子能量關系Fig.2 The relationship of energy between oscillators

(13)

(14)

大于或等于此臨界值時，函數關系式只存在一個極值點，函數單調遞增，不會出現非線性跳躍現象，系統不能實現能量傳遞，故要實現系統TET，NES阻尼必須滿足關系式

(15)

當阻尼滿足此關系時，函數關系具有兩個極值點，能夠出現非線性跳躍，在滿足一定的初始條件后即能夠實現TET。可見NES的阻尼條件是保證系統能夠實現TET的前提條件，這個條件與主結構的固有頻率有關。

3系統阻尼討論

3.1能量耗散與參數關系

當主結構阻尼足夠大時，不管NES阻尼參數如何設計，系統能量完全可以通過主結構阻尼耗散掉，顯而易見，要NES能夠實現減振的效果，主結構阻尼必須小于某個臨界值。上一節通過討論得到了NES阻尼的臨界值，這一節同樣用TET發生為條件，尋求NES具有吸振能力時，主結構阻尼必須滿足的條件。

(16)

當系統的阻尼均為0時，即λ1=λ2=0，上式表示對應保守系統的能量，即

(17)

X2(s)=

(18)

再對式(18)進行Laplace反變換有

H(t1)=

式中:H(0)表示系統的初始能量。通過式(19)可以知道，系統的能量完全可以通過系統阻尼參數表示，為了便于分析將上式的積分項Taylor展開

(20)

(21)

同理有式

(22)

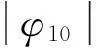
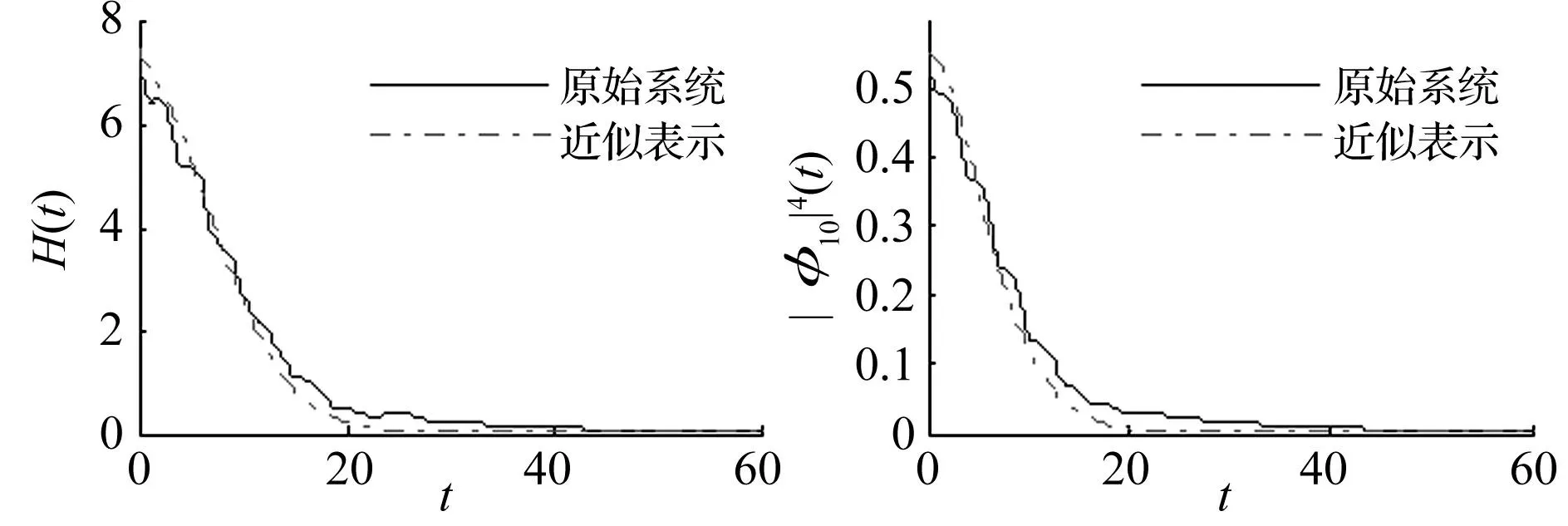
圖3　能量響應對比Fig.3 Energy response comparison

3.2阻尼關系討論

上一小節我們討論得出可以通過式(19)來近似的表示原系統，這一節討論同樣利用這個關系式。注意到式(19)有阻尼參數的特殊關系，即

δλ2-λ1=0

(23)

那么系統的能量耗散

H(t0)=H(0)exp(-λ1t0)

(24)

在該種情況下系統的能量耗散只與初始條件和主結構阻尼有關，此時耦合NES的系統內部仍然可以發生能量的相互傳遞，但是并會減少系統的總能量，NES不再具有減振作用。可見阻尼關系式(23)是系統能量傳遞的一個臨界值條件。討論兩種情況：

(1)δλ2>λ1時

與該系統對應的非耦合NES系統的能量耗散為

H0(t1)=H(0)exp(-λ1t1)

(25)

將式(20)代入式(19)可以獲得耦合NES系統的能量耗散關系。為了研究NES是否具有減振效果，可以以NES耗散系統能量為衡量標準。作能量差

ΔH=H0(t)-HNES(t)

(26)

那么結合式(21)有

ΔH=H(0)e-δλ1t-

(27)

注意到式中(27)中還有一個關系

(28)

此時的前提條件是系統的初始能量全部集中于主結構振子中。式(27)中有初始條件的Taylor展開，用數學歸納法不難證明

ΔHmin(t)=H0(t)-HNES(t)≥0

(29)

既有在滿足關系δλ2>λ1時，對于有限時間內系統能量差大于0恒成立。此時的ΔH由NES來吸收，此時NES不僅能夠與主結構發生能量的相互傳遞，還能達到吸收主結構能量的目的，從而實現減振的目的。

(2)δλ2<λ1時

在該種情況下，同樣方法可以證明能量差的最小值一定小于0，那么有如下關系

?tc>0使得ΔH(tc)=0

(30)

此時系統雖然滿足能量相互傳遞的條件，但是能量傳遞經過一個周期以后又返還給了主結構，所以存在能量為0的時刻，其中tc并不唯一。這種情況下NES雖然能夠相互傳遞能量，但是并不能達到減少主結構振動能量的目的。

綜述(1)和(2)兩種情況分析結果，在有阻尼系統中，若要NES能夠實現TET以達到減振的目的，系統阻尼必須滿足條件

δλ2>λ1?λ2>ελ1

(31)

在式(15)中給出了NES阻尼的有效范圍，結合式(31)可以得到如下關系

(32)

式(32)中不難得出，當主結構阻尼λ1足夠大時，NES的阻尼范圍可能出現空集的可能，此時NES不再具有減振效果，主結構振動完全可以通過λ1減小振動。如果將主結構寫成具有標準形式的振動方程，即

(33)

可以利用關系

2ξω0=ελ1

(34)

結合該關系和式(32)可以得出主結構阻尼范圍

(35)

不難發現主結構阻尼的有效范圍是一個常值，與系統的其它參數無關。主結構的微分方程變換為標準方程，當阻尼大于臨界值ξcr時，系統可以通過自身阻尼達到減小振動的目的；當阻尼小于臨界值ξcr時，則通過耦合NES的方法去減小主結構振動。

在工程應用中，當結構可以簡化為線性的單自由度系統，并受到一個沖擊載荷時，在結構阻尼比大于臨界值時，系統可以通過自身阻尼的作用減小振動，但減振效率低，抑制效果差，振動抑制措施需要其它方法；當結構的阻尼比小于該臨界值時，可以通過耦合單自由度NES結構的形式實現高效、快速的振動抑制。

4數值驗證

4.1阻尼關系

上一部分我們理論分析了耦合NES的單自由度線性振子的系統阻尼必須滿足關系λ2>ελ1，這一節我們用四階Runge-Kutta數值方法，將非耦合NES的振子系統與耦合NES的振子系統進行對比分析，數值驗證上述結論。

在圖 4(a)中的阻尼參數滿足關系λ2<ελ1(λ1=0.5,λ2=0.03)，非耦合NES的振子即實線，振子能量一直在緩慢減小，需要耗散能量時間很長。對于耦合NES的系統，能量耗散情況略有不同，能量呈現震蕩形式，在很短的一段時間內能量急劇減少，但同樣在一段時間內主振子能量又迅速恢復到一定的程度，經過多個周期后能量耗散完畢，耦合的NES振子只是起到一個能量傳遞的作用。對于兩個振子能量變化曲線存在明顯的交點，在交點處有關系ΔH=0，即耦合NES的系統在經過一個周期后，主振子剩余的能量與非耦合NES的系統經過相同時間后所剩余的能量是一樣的，雖然在非耦合NES的系統中能量發生了傳遞，但是NES并沒有耗散能量，NES只起到一個能量傳遞的作用，沒有減振效果，系統能量的減少仍像非耦合NES的系統一樣，均由主結構阻尼吸收。

圖 4(b)阻尼參數滿足關系λ2=ελ1(λ1=0.5，λ2=0.04)時對應的能量響應曲線，從圖中不難發現，此時兩條曲線雖然沒有明顯的交點，但是總體能量傳遞趨勢與圖4(a)類似，在此阻尼參數下，一周后能量差值很小，NES只耗散很小的一部分能量，系統大部分能量仍由主結構吸收，NES并不能實現高效減振的目的。

圖4　能量響應對比Fig.4 Energy response comparison

圖5(a)和圖5(b)是系統阻尼均滿足關系λ2>ελ1時對應的能量變化曲線，對于耦合NES的系統，能量在一個周期內急劇減少，雖然也出現了振子間能量相互傳遞，但是傳遞的能量很少，與非耦合NES系統相對比，NES實現了高效的能量轉移，在第一個周期內就吸收了主振子90%以上的能量，并且耗時很短。可見只有在系統阻尼滿足關系λ2>ελ1時，NES才能實現TET從而達到減振的目的。圖5(a)λ1=0.5,λ2=0.3；(b)λ1=0.5,λ2=0.2。為了更加直觀的對比耦合NES與非耦合NES系統的減振效果，在圖6中為主結構振子的幅值響應曲線，圖6(a)系統附有NES振子，圖6(b)為非耦合NES的系統，不難發現附有NES振子的系統幅值衰減很快，NES吸收主結構振子能量明顯。數值證明了只有系統阻尼滿足關系λ2>ελ1，NES才能實現TET，具有高效減振效果。

圖5　能量響應對比Fig.5 Energy response comparison

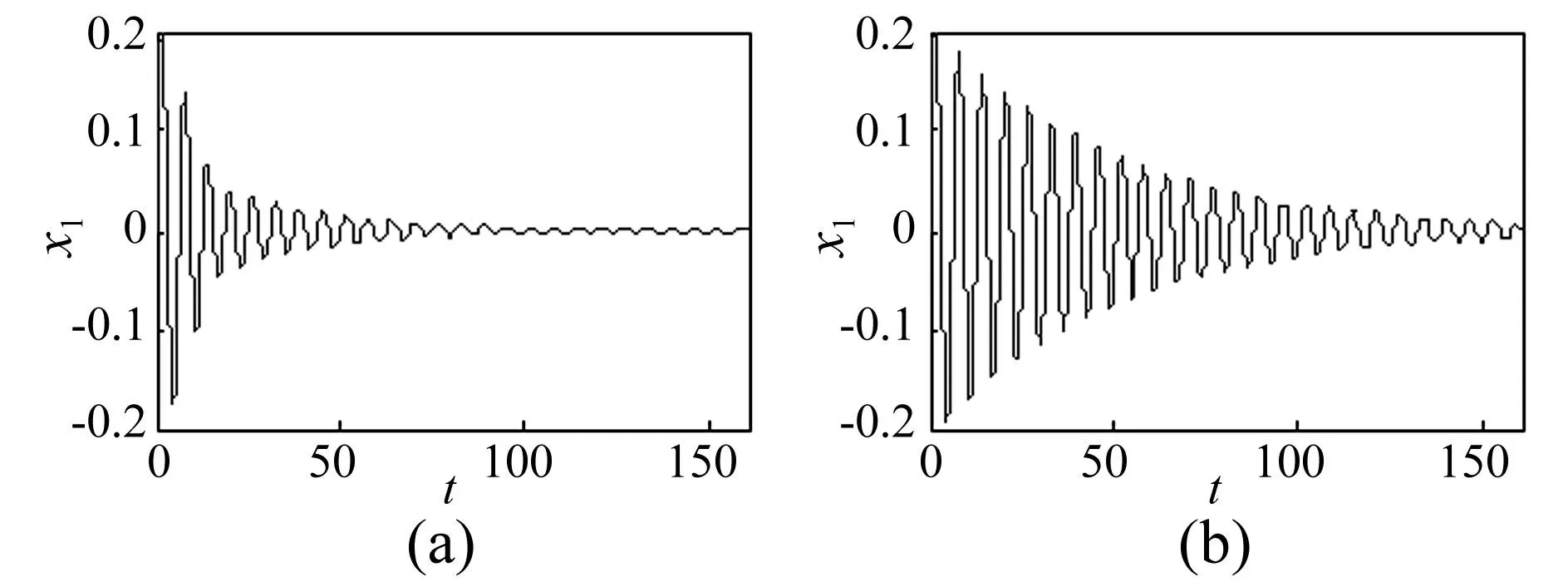
圖6　主結構幅值響應Fig.6 Amplitude response of main structure

4.2主結構阻尼范圍驗證

系統減振能力的評價可以用耗散時間來表示，即系統耗散初始總能量的η(0<η<1)所用的時間，這里取η=1-1/e=63.21%來衡量[12]。對于非耦合NES的系統，將微分方程轉換成標準方程，阻尼為ξ，用復變量平均法可以將微分方程轉變成形式

(36)

對上式共軛復變換有

(37)

那么有

(38)

式中:C0與初始條件有關，可以求得

(39)

同樣系統的能量可以表示成形式

(40)

不難求得耗散時間td

(1-η)E(0)

(41)

對于耦合NES的主結構系統，可以用式(19)近似求得系統的耗散時間，結合式(21)經過簡單的數學推導可以得到當初始能量全部集中于主振子時，耦合NES的系統的耗散時間td可以式(41)相似的推導過程，可以得到關系

{1+[λ2-2ε(λ1+λ2)td]}

exp(1-λ2td)=1

(42)

借助數學工具軟件上式求解是很容易的。在圖7中非耦合NES主結構與耦合NES主結構的耗散時間對比圖。圖 7(a)為非耦合NES系統(實線)與耦合NES系統(虛線)耗散時間對比圖，從圖7(a)可知，阻尼比約大，所需的耗散時間約長，當阻尼比大于臨界值ξcr=0.227 8時，系統的耗散時間曲線基本重合的，主結構能夠完全依靠自身的阻尼抑制振動，增加NES只能使結構冗余，無作用；當主結構阻尼比小于臨界值ξcr時，NES能夠大幅度縮減耗散時間，而且阻尼主結構阻尼比越小，NES振動抑制效果明顯。圖 7(b)耦合NES系統不同NES阻尼對應的耗散時間對比圖。可見經數值驗證，理論推導的臨界值是有效的。

圖7　阻尼與耗散時間關系Fig.7 Relationship between damp and time of dissipation

5結論

本文以耦合非線性能量阱系統的定向能量傳遞為出發點，基于復變量平均法分析系統能量耗散與系統各參數相互關系，通過研究函數關系特殊點討論系統對應的力學特性。得到以下三個結論：

(1)耦合非線性減振器的非保守系統中，系統發生定向能量傳遞的前提條件是非線性能量阱阻尼必須小于某一定值，該定值與主結構固有頻率有關；

(2)初始能量全部集中于耦合非線性能量阱的主結構時，系統阻尼必須滿足一定的關系才能使非線性減振器實現定向能量傳遞；

(3)線性振子阻尼在小于臨界值0.2278時，非線性能量阱才具有吸振能力，并且線性振子阻尼越小，合理設計非線性能量阱后吸振效果越佳。

數值仿真驗證了上述結論。

參考文獻

[1]Barry H, Khaki M, Mark S, et al. Advancing ORS technologies and capabilities with a space tourist suborbital vehicle[C]//AIAA SPACE 2009 Conference. California. 2009:14-17.

[2]Andrew D S.QuickSAT/step_SATdb-A satellite concurent design automation and design for manufacturabillty cloud based environment for PnP based satellites[J]. AIAA.2011:29-31.

[3]Gendelman O V, Manevitch L I, Vakakis A F. Energy pumping in nonlinear mechanical oscillators: Part I Dynamics of The underlying Hamiltonian systems[J]. Journal of Applied Mechanics, 2001, 68(1): 34-41.

[4]Vakakis F, Gendelman O V. Energy pumping in coupled mechanical oscillators, Part II: resonance capture[J]. Journal of Applied Mechanics, 2001, 68: 42-48.

[5]Manevitch L I.The description of localized normal modes in a chain of nonlinear coupled oscillators using complex variables[J]. Nonlinear Dynamics, 2001, 25: 95-109.

[6]Gendelman O V, Gorlov D V, Manevitch L I, et al. Dynamics of coupled linear and essentially nonlinear oscillators with substantially different masses[J]. Journal of Sound and Vibration, 2005, 286: 1-19.

[7]張也弛,孔憲仁,張紅亮.非線性耦合振子間的靶能量傳遞研究：保守系統中的完全傳遞[J]. 振動與沖擊,2012, 31(1):150-155.

ZHANG Ye-chi, KONG Xian-ren, ZHANG Hong-liang. Targeted energy transfer among coupled nonlinear oscillators: complete energy exchange in a conservative system[J]. Journal of Vibration and Shock, 2012, 31(1): 150-155.

[8]Manevitch L I, Gourdon E, Lamarque C H. Towards the design of an optimal energetic sink in a strongly inhomogeneous two-degree-of-freedom system[J].Journal of Applied and Mechanics, 2007, 74:1078-1086.

[9]張也弛,孔憲仁.非線性耦合振子間產生靶能量傳遞的初始條件[J]. 哈爾濱工業大學學報,2012, 44(7): 21-26.

ZHANG Ye-chi, KONG Xian-ren.Initial conditions for targeted energy transfer in coupled nonlinear oscillators[J]. Journal of Harbin Institute of Technology, 2012, 44(7):21-26.

[10]Nguyen T A, Pernot. S. Design criteria for optimally tuned nonlinear energy sinks Part I: transient regime[J]. Nonlinear Dynamics, 2012, 69: 1-19.

[11]Sapsis P H, Quinn D D, Vakakis A F. Effective stiffening and damping enhancement of structures with strongly nonlinear local attachments[J]. Journal of Vibration and Acoustics, 2012, 134: 1-12.

[12]Manevitch L I, Musienko A I, Lamarque C H. New analytical approach to energy pumping problem in Strongly Nonhomogeneous 2dof System[J]. Meccanica, 2007, 42: 77-83.