汽車制動間隙自調臂的分離間隙提取技術研究

江文松，羅　哉，郭　斌，范偉軍，陸　藝

(1. 北京航空航天大學儀器科學與光電工程學院，北京　100191； 2. 中國計量學院計量測試工程學院，杭州　310018；3. 杭州沃鐳科技有限公司，杭州　310018； 4. 浙江大學光電信息工程學院,杭州　310012)

第一作者江文松男，碩士生，1988年生

汽車制動間隙自調臂的分離間隙提取技術研究

江文松1,2，羅哉2，郭斌3，范偉軍2，陸藝4

(1. 北京航空航天大學儀器科學與光電工程學院，北京100191； 2. 中國計量學院計量測試工程學院，杭州310018；3. 杭州沃鐳科技有限公司，杭州310018； 4. 浙江大學光電信息工程學院,杭州310012)

摘要：基于線性Radon變換的圖像投影方法，改善汽車自動調整臂性能測試儀對分離間隙的提取精度。由于工業領域廣泛使用的梯度極值法等傳統特征點提取方法對含噪密集的信號非常敏感，很難準確識別在線測試曲線的拐點，降低了曲線特征點的提取精度，增加了誤判率。在分離間隙在線測試儀的應用中，基于線性Radon變換法的分離間隙提取技術，能大大改善分離間隙的獲取精度和準確度。實驗驗證，線性Radon變換法的計算誤差比梯度極值法的計算誤差至少降低10倍，同時，該技術理論研究成果已在杭州沃鐳科技有限公司成功推廣使用。

關鍵詞：自調臂性能測試儀；線性Radon變換；分離間隙提取；制動間隙自調臂

基金項目：國家自然科學基金項目(51005220);國家質檢總局公益性行業科研專項項目(201210109)

收稿日期：2014-01-27修改稿收到日期：2014-05-29

通信作者羅哉男，博士，副教授，碩士生導師，1979年生

中圖分類號:U467.3; TP391.4

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.11.011

Abstract:Here, the linear Radon transformation was applied in a separating clearance on line test system of an automatic brake adjuster to get a separating clearance. The linear Radon transformation was widely used to extract inflection points of an online test system, especially, under noise conditions. Traditional characteristic point extraction methods like the gradient maximum optimal method were widely used in industry areas. Since they were sensitive to signals containing strong noise, those traditional methods are hard to identify the inflection points from online tested curves with signals containing strong noise. Compared with the linear Radon transformation, tradition methods have a much less accuracy of inflection points extraction when applied in a separating clearance online test system of an automatic brake adjuster. The experimental results showed that the computational error of the linear Radon transformation is over 10 times lower than that of the gradient maximum optimal method. The separation clearance extraction technology was successfully used at Hangzhou Wolei tech. Co., LTD.

Separating clearance extraction technology for automatic brake adjusters

JIANGWen-song1,2,LUOZai2,GUOBin3,FANWei-jun2,LUYi4(1. School of Instrumentation Science & Opto-electronics Engineering, Beihang University, Beijing 100191, China; 2. College of Metrology & Measurement Engineering, China Jiliang University, Hangzhou 310018, China; 3. Hangzhou Wolei Technology Co., LTD., Hangzhou 310019, China; 4. Photoelectric information engineering institute, Zhejiang University, Hangzhou, 310012, China)

Key words:tester of automatic brake adjuster; linear Radon transformation; extraction of separating clearance; automatic brake adjuster of vehicle

汽車制動間隙自動調整臂(以下簡稱自調臂)主要應用在公交客車、農用機車及重載貨車的制動系統上，是保證汽車制動系統安全可靠的重要部件。自調臂的分離間隙是自調功能穩定性的量值評定指標。自調臂的分離間隙在線測試系統中，測試曲線的分離間隙往往只有0.3～0.8 mm,其提取精度受算法的影響較大。理想情況下，力/位移測試曲線由三段斜率不同的直線組成，在外部干擾信號等因素的影響下，測試曲線是帶有低頻噪音信號和拐點模糊的三段近似直線。

梯度極值法等傳統方法是提取特征點的常用技術，但該法對曲線的平滑性依賴較大，因其容易誤判拐點，故不適于提取含有噪音信號的在線測試曲線特征點[1-2]。計量檢測機構常用散件測量法通過電感測微儀檢測自調臂的分離間隙，但在實際生產中，由于該檢測方法費用昂貴，操作復雜且檢測周期長，不適合生產廠家的批量檢測[3]。在現有的特征點檢測算法中，最小二乘擬合法通過計算離散點間的近似曲率來實現特征點提取，但其易受噪音等影響而產生偽拐點，影響計算精度[4]。基于Harris和HarrisZ算法的特征點檢測方案雖然能有效快速的識別特征點，但是無法保留特征點的尺度信息，從而不能用于計算分離間隙的大小[5]。基于SIFT算法[6]在大尺度空間提取特征點方面具有非常廣泛的應用，并能有效識別方向信息，但其算法的復雜性較高，在特征點提取的建模上將會耗費大量的時間，因此無法滿足批量工件檢測的要求。而本文提出的線性Radon變換法具有很強的抗噪抗干擾能力，對在線數據進行線性Radon變換，并擬合出光滑的三段直線后，利用交線關系求取三段線的兩個拐點，從而計算出分離間隙值，該算法誤差小，精度高，計算速度快，魯棒性好，實現方便。

1自調臂的工作原理

自調臂的控制臂固定在車軸上，殼體安裝在制動氣缸上作為施力元件。自調臂的蝸輪通過齒輪軸與制動器的凸輪相連接，構成了傳遞制動力和感知制動間隙的閉環回路。制動襯片一旦磨損引起蹄鼓間隙增大，自調臂就能在制動過程中感知其超量值，并在制動回位時自動補償超量間隙，使蹄鼓間隙恢復到預設的標準值，其結構見圖1[7-9]。

單向離合器是實現自調功能的主要部件，由圖1中的3,4,5組成。分離間隙反映了單向離合器錐齒輪的嚙合狀況，是蝸桿在臂體內一端到軸套之間的活動距離。分離間隙過大，會使離合器與蝸桿之間的齒輪出現傳動打滑，導致自調量偏小；分離間隙過小易引起單向離合器的離合紊亂，甚至會使單向離合器卡死。

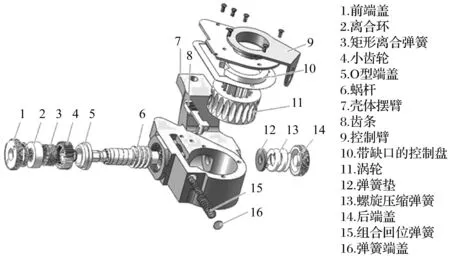
圖1　自調臂結構圖Fig.1 Structure of automatic brake adjuster

2線性Radon變換法提取分離間隙

通過多個角度的Radon變換可實現分段函數的拐點提取，對f(x,y)沿路徑L：y=px+τ進行線性Radon變換[10-15](見圖2)。

圖2　Radon變換的坐標表示形式Fig.2 Coordinate representation of Radon transformation

則在參數域(v,φ)下的Radon變換公式為

Rf(v,φ)=

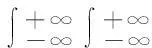
(1)

式中:δ為Dirac函數；v為L到原點的垂直距離，v∈(-∞,+∞)；φ為L與X軸的夾角，φ∈(0,π)。

當f(x,y)為垂直于L的直線段時，經過Radon變換的f(x,y)會在L平面上投影成一個波峰，該波峰由f(x,y)上的點云沿uo方向匯聚而成。

在進行分離間隙測試時，理想情況下的力/位移測試曲線設為y，曲線由4段斜率不同的直線段組成(見圖3)。

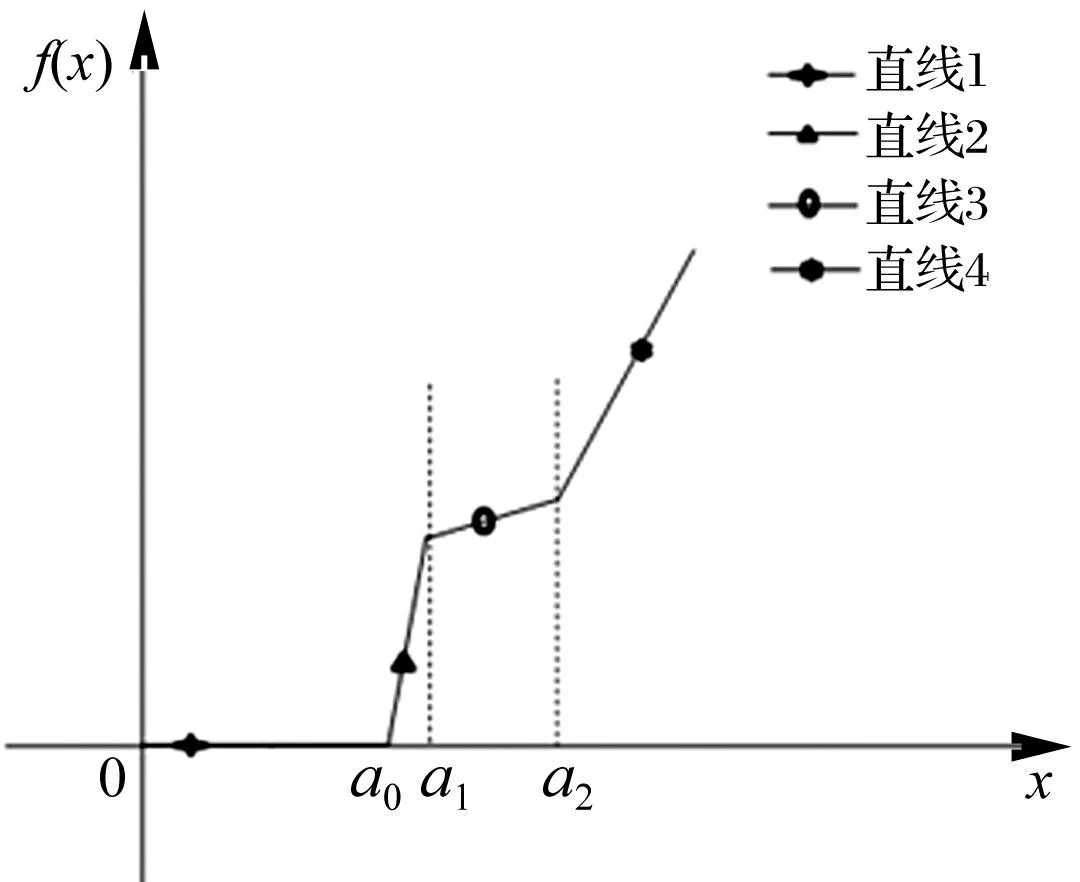
圖3　分離間隙理想測試曲線Fig.3 Ideal test curve of separation

設其斜率為pi(i=1,2.3)，直線y的方程為

(2)

式中:p2對應直線3的斜率，為壓縮彈簧的勁度系數。

將式(2)代入(1)中，得

Rf(v,φ)=

φ∈[0,π]

(3)

式(3)即為曲線y在180°上的Radon變換。對于斜率不同的多段連續線段y，經過180°的線性Radon變換，將會按y的各段法向路徑轉換成點狀云圖，而斜率發生明顯變化的兩段直線的拐點處的投影云圖則呈現點云峰值。投影后的圖像及點云峰值見圖4。

圖4　分離間隙理想測試曲線的線性Radon變換圖Fig.4 Image oflinear Radon transformation about Ideal test curve of separation

圖4中的四個峰值即為線性Radon變換后的拐點值，分別根據點云峰值處的坐標信息，擬合對應曲線的理想直線方程，聯立直線方程即得拐點。坐標x軸為投影法線的角度變化量，設為βi(i=0，1,2,3)，分別為四段直線(包括水平直線)與x軸夾角的補角，根據該點的極坐標值(ri,βi)求出映射在X-Y坐標軸上的點(xi,yi)。

式中：ri為對應峰值點在投影軸上的相對位置；i=0，1,2,3。

對應直線的斜率pi=tan(βi-90)。

除水平線之外，分別求出三段直線的方程式，

y=pi(x-xi)+yi,(i=1，2,3)

(4)

將式(4)代入式(2)得τi=yi-pixi

因此，分離間隙?求得：

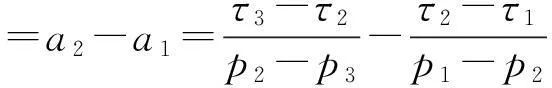
(5)

3測試系統的設計

1.微動平臺加載電機 2.導頭瞄準電機 3.位置傳感器 4.扭矩傳感器 5.壓力傳感器 6.六方導頭 7.被測件(自調臂) 8.調節桿 9.后端蓋調節電機 10.微動平臺 11.支承與調整平臺圖5　分離間隙測試系統Fig.5 Test system of separation

自調臂分離間隙測試系統主要包括分離間隙測量模塊、微動平臺控制模塊、氣動支承與調整模塊、后端蓋調節模塊四個部分，測試裝置的三維結構見圖5。利用該測試系統對自調臂分離間隙進行測試，測試步驟見圖6。

圖6　測試流程圖Fig.6 Flow chart of the test

鑒于夾具的設計對測試系統的精度及穩定性影響很大[16-18]，為了單獨論證特征點提取算法對分離間隙提取精度的影響，故本文中使用的三種算法，其測試數據的捕獲均在同一夾具上實施的，從而消除了測試設備的精度對特征點提取算法的影響。本系統專門設計的支承與調整平臺通過反饋控制原理實現平臺的二維位置微調，故它可裝夾國內不同型號自調臂。在自調臂裝夾時，支承夾具氣缸的壓緊力最高可達1.0 MPa，保證了系統的穩定和測試的可靠進行。為了使測試系統的測試結果符合仿真狀況下自調臂參數的動態變化，系統及夾具完全按照實車制動系設計而來，從而保證了測試結果的真實性。

記錄每次測試的壓力/位移數據，測試曲線見圖7。

圖7　實時測試曲線Fig.7 Online test curve

圖7所示的力/位移曲線與圖3曲線特征相似，其中，第2段線為壓力克服自調臂壓縮彈簧的預緊力過程；此后，壓縮彈簧開始收縮，蝸桿端面和單向離合器分離，即圖中第3段線；當二者完全分離，蝸桿左端面接觸殼體內腔壁，蝸桿將產生彈性形變，即第4段線。所求分離間隙即為第3段線投影在x軸上的長度。

4實驗與結果分析

試驗的10個調整臂是以散件組裝的形式安裝的。在安裝螺旋壓縮彈簧和后端蓋之前，安裝好其它散件并固定自調臂殼體，用散件測量法通過電感測微儀檢測每個自調臂蝸桿右側端面在臂體內的軸向活動距離，即自調臂的分離間隙，對每個被測件分別測量5次求取平均值。該法是計量站標定調整臂分離間隙的常用手段，故本實驗將該均值作為實驗參考值，測試結果見表1。

利用上述分離間隙測試系統，分別測試10個被測自調臂的分離曲線，將測試曲線分別經過線性Radon變換法、梯度極值法和最小二乘法處理，提取曲線拐點求分離間隙。

(1)10個被測件的測試曲線經線性Radon變換后的圖像見圖8。

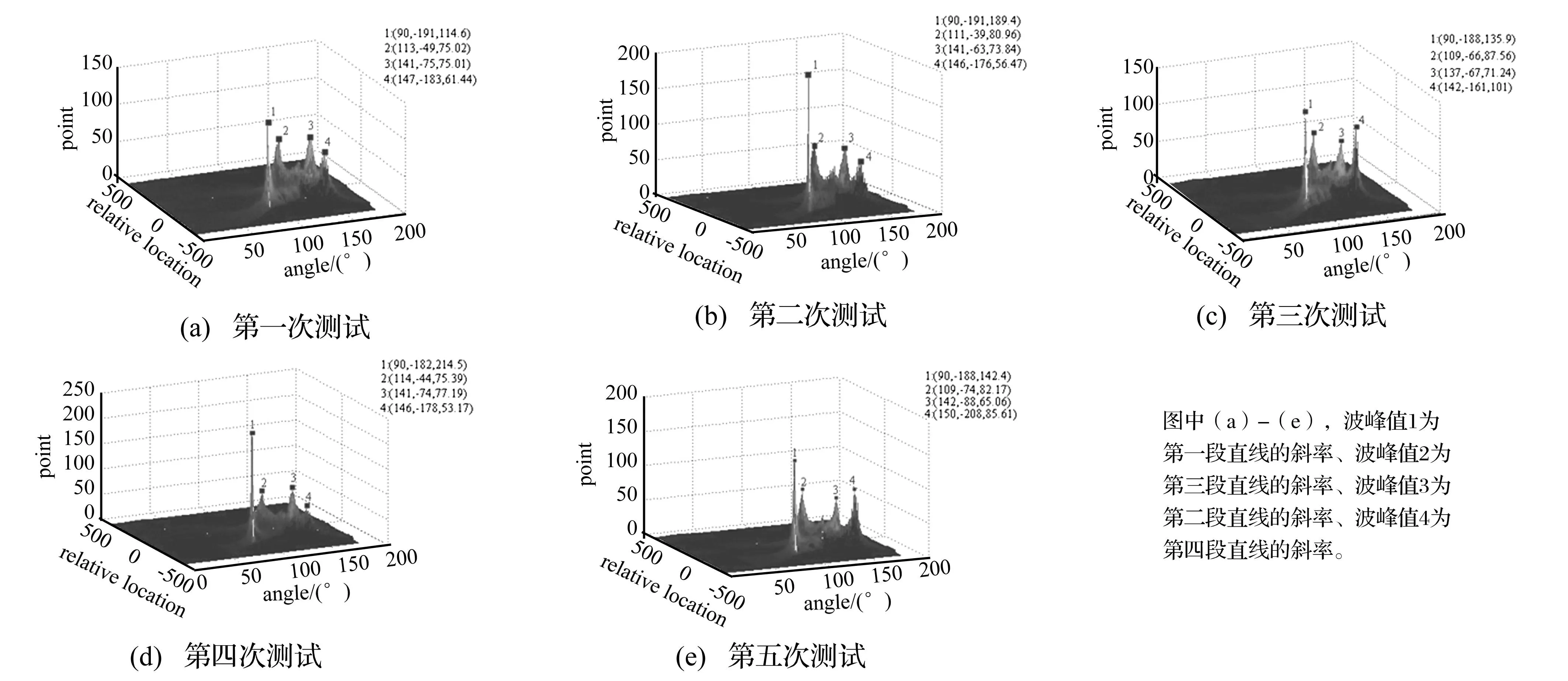
圖8　五次測試結果的Radon變換圖Fig.8 Images of Radon transformation result

通過Radon投影的峰值坐標信息，擬合出實際測試曲線，利用式(5)計算出10次測試的分離間隙值，每個被測件測量5次求取平均值,計算結果見表1。

(2)用梯度極值法對10個被測件的測試結果進行算法處理，每個被測件測量 5次求取分離間隙平均值。該算法的原理為對曲線方程求二階導數，二階導數的極值點即為對應曲線的拐點，計算結果見表1。

(3)用最小二乘擬合法對10個被測件的測試曲線進行擬合處理。該算法的基本原理為根據點集的分布擬合特征直線，將力/位移曲線y=P(xi)=pix+τi作為分離間隙經驗模型，使得分離間隙實測值Ρ(xi)與參考值?i差值的平方和最小。梯度極值法和最小二乘擬合法兩種算法的結果比較見圖9。

表1　不同算法下的分離間隙值比較結果

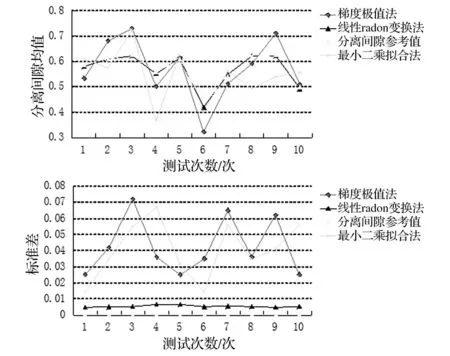
圖9　兩種算法結果比較Fig.9 The comparison results with different algorithm

5結論

(1)上述結果顯示，梯度極值法和最小二乘法的標準差遠大于線性Randon變換法的標準差，同時，線性Randon變換法的標準差最接近參考值的標準差。表明在提取分離間隙的算法當中，線性Randon變換法比梯度法和最小二乘擬合法都穩定。

(2)將參考值作為真值，線性Radon變換法的計算結果的相對平均誤差為±0.01，梯度極值法的計算結果的相對平均誤差不小于±0.10，最小二乘擬合法的相對平均誤差不小于±0.12。比較表明，線性Radon變換法比梯度極值法的計算誤差低10倍以上，比最小二乘擬合法的計算誤差低12倍以上。

(3)在自調臂分離間隙的提取技術上，線性Radon變換法的提取技術要由于傳統算法，因此，未來在工業測試曲線的特征點提取上使用線性Radon變換技術，可以改善和提高測試儀的測試精度。

參考文獻

[1]Felhi M, Bonnier N, Tabbone S. A robust skew detection method based on Maximum Gradient Difference and R-signature[J]. Image Processing (ICIP), 2011:2617-2620.

[2]Tohmé M, Lengellé R. Sequential maximum gradient optimization for support vector detection[J]. European Signal Processing Conference,2009:1705-1709.

[3]ISO 463-2006,產品幾何量技術規范(GPS).尺寸測量設備.機械千分表的設計和計量學特性[S].倫敦：英國標準協會，2006.

[4]秦濤,張軻,鄧景煜,等. 基于改進最小二乘法的焊縫特征直線提取方法[J]. 焊接學報,2012,33(2):33-38.

QIN Tao, ZHANG Ke, DENG Jing-yu, et al. The extraction method of weld line based on the improved least square method[J]. Transactions of the China Welding Institution,2012,33(2):33-38.

[5]Bellavia F, Tegolo D, Valenti C. Improving harris corner selecion strategy[J]. IET Computer vision, 2011,5(2):87-96.

[6]申鉉京,朱葉,呂穎達,等. 基于SIFT和HSI模型的彩色圖像復制-粘貼盲鑒別算法[J]. 吉林大學學報:工學版,2014, 44(1):171-176.

SHEN Xuan-jing, ZHU Ye, Lü Ying-du, et al. Coloured image copy-move forgery detection based on SIFT and HSI[J].Journal of Jilin University:Engineering and Technology Edition, 2014, 44(1):171-176.

[7]羅哉,江文松,陸藝,等.汽車自動調整臂螺旋壓縮彈簧的失效建模[J]. 中國機械工程,2013,24(12):1596-1599.

LUO Zai,JIANG Wen-song, LU Yi, et al. The failure model of helical compression spring for automatic brake adjuster[J]. China Mechanical Engineering,2013,24(12):1596-1599.

[8]王軍, 賴峰. 制動間隙自動調整臂的設計原理[J]. 汽車科技, 2006(2): 7-10.

WANG Jun, LAI Feng. Design principle of automatic brake adjuster[J]. Auto Mobile Science & Technology, 2006(2):7-10.

[9]External Automatic Slack Adjuster Test Procedure[S]. SAE document, J1462-1994.

[10]張根輩,臧朝平. 基于振動測試的非線性參數識別方法[J]. 振動與沖擊,2013,32(1):83-88.

ZHANG Gen-bei,ZANG Chao-ping. A novel method for nonlinear parametricidentification based on vibration tests[J].Journal of Vibration and Shock,2013,32(1):83-88.

[11]謝松法. 模式特征的提取與應用研究[D]. 武漢：華中科技大學 2007.

[12]Sugimoto K, Tomita F. Boundary segmentation by detection of corner, inflection and transition points [J]. Visualization and Machine Vision, 1994:13-17.

[13]張慧杰,郭志平,司景萍,等. 汽車懸架整車動力學模型的參數辨識[J]. 振動與沖擊, 2013(23):145-150.

ZHANG Hui-jie,GUO Zhi-ping, SI Jing-ping,et al.Parametric identification of a vehicle suspension dynamic model[J]. Journal of Vibration and Shock,2013(23):145-150.

[14]Rouze N C, Wang M H, Palmeri M L,et al.Robust estimation of time-of-flight shear wave speed using a Radon sum transformation[J]. Proc. IEEE Ultrason. Symp,2010:21-24.

[15]Krause M, Hausherr J M, Krenkel W. (Micro)-Crack detection using local Radon transform[J]. Materials Science and Engineering A,2010:7126-7131.

[16]Deckers K, Guillaume P, Lefeber D, et al.. Turning point based fatigue testing: Combining multisines with turning point replication[J]. Mechanical Systems and Signal Processing,2012:23-31.

[17]Satheesh Kumar R M, Asokan P, Kumanan S. Design of loop layout in flexible manufacturing system using non-traditional optimization technique[J]. International Journal of Advanced Manufacturing Technology,2008:594-599.

[18]Lemos M A, Brunini D M, Botura G,et al.Virtual instrumentation: A practical approach to control and supervision process[J]. Computer Science and Network Technology (ICCSNT),2011:2570-2573.