考慮齒輪-轉子系統振動響應的最佳修形曲線研究

馬　輝，逄　旭，宋溶澤，聞邦椿

(東北大學機械工程與自動化學院，沈陽　110819)

第一作者馬輝男，博士，副教授，1978年生

考慮齒輪-轉子系統振動響應的最佳修形曲線研究

馬輝，逄旭，宋溶澤，聞邦椿

(東北大學機械工程與自動化學院，沈陽110819)

摘要：輪齒修形可減小齒輪靜態傳動誤差，改善齒輪動態特性。基于現有文獻，考慮基圓與齒根圓不重合，在齒廓精確建模的基礎上確定齒輪的時變嚙合剛度和靜態傳動誤差。針對不同修形曲線在不同修形量下齒輪靜態傳動誤差的變化進行分析，給出了不同修形量范圍內的最佳修形曲線，并結合齒輪-轉子系統動力學模型，考慮齒廓修形引起的無載荷靜態傳動誤差，分析不同修形曲線下系統的振動特性，進一步確定不同轉速下最佳修形曲線。研究結果表明通過評估齒輪-轉子系統的振動特性，可更好地確定不同轉速下的輪齒的最佳修形曲線。

關鍵詞：齒廓修形；時變嚙合剛度；靜態傳動誤差；齒輪-轉子系統；振動響應

基金項目：中央高校基本科研業務費專項資金資助(N130403006);教育部新世紀人才支持計劃(NCET-11-0078)

收稿日期：2014-01-08修改稿收到日期：2014-05-07

中圖分類號:TH113

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.11.004

Abstract:Tooth profile modification can decrease the loaded static transmission error, and improve the dynamic characteristics of gear pairs. Here, based on available theories and literatures, the time-varying mesh stiffness (TVMS) and static transmission error (STE) were determined with a correction method considering misalign effect between the root circle and tooth base circle and an accurate gear profile curve. The optimal profile modification curves with different amounts of profile modification were determined by analyzing the STE changing with different profile modification curves and different amounts of profile modification. Combining a gear-rotor system dynamic model and considering the effect of no-load STE caused by profile modification, the vibration responses of the gear-rotor system with different gear profile modification curves were analyzed to determine the optimal profile modification curves at different rotating speeds. The results showed that the optimal gear profile modification curves at different rotating speeds can be determined by evaluating the vibration responses of the gear-rotor system.

Optimal profile modification curves for spur gears considering vibration responses of a gear-rotor system

MAHui,PANGXu,SONGRong-ze,WENBang-chun(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

Key words:profile modification; time-varying mesh stiffness; static transmission error; gear-rotor system; vibration response

受制造、安裝誤差、齒輪彈性變形及熱變形等的影響，齒輪嚙合時不可避免地產生沖擊、振動和偏載，導致齒輪早期失效的概率增大。生產實踐和理論表明，適當的輪齒修形，對改善齒輪運轉性能、提高承載能力、延長使用壽命有明顯的效果[1]。

許多學者對齒廓修形問題進行了研究，通過建立齒輪三維有限元模型，Ohno等[2]分析了接觸壓力和斜齒輪修形量的關系，確定了斜齒輪的最佳修形量。基于非線性接觸理論，Wagaj等[3]建立二維、三維斜齒輪副接觸有限元模型，分析了直線、拋物線齒頂修形以及齒向修形對斜齒輪靜態傳動誤差的影響。Li[4]使用有限元法研究了加工誤差、裝配誤差和齒向修形對直齒輪輪齒表面接觸應力、齒根彎曲應力、載荷分布和靜態傳動誤差的影響。通過建立的直齒輪副有限元模型，Tharmakulasingam等[5]研究發現齒廓修形能降低齒頂、齒根應力以及靜態傳動誤差的幅值，并且靜態傳動誤差會隨著扭矩增大而增大。Tesfahunegn等[6]采用非線性有限元方法分析齒形修整對傳動誤差、接觸壓力以及齒根應力的影響。Tavakoli等[7]對直線修形和曲線修形下的靜態傳動誤差進行了頻率分析，表明傳動誤差變化越平滑，波動幅值越小，齒輪傳動越平穩。Ma等[8]通過Ansys軟件建立了齒頂修緣的直齒輪嚙合有限元模型，主要研究了齒頂漸開線修緣對齒輪-轉子系統振動響應的影響。Chen等通過建立解析模型，研究了齒廓修形、扭矩及齒根裂紋對齒輪嚙合剛度、負載分配及有載荷靜態傳動誤差的影響。

從現有的文獻來看，針對齒廓修形，大多關注于載荷分布，靜態傳動誤差及齒輪副的振動特性，對于最佳修形曲線的確定，也僅限于修形量一定的情況。本文基于Chen等[9]建立的解析模型，獲得齒輪時變嚙合剛度和靜態傳動誤差，分析了不同修形量范圍內的最佳修形曲線，并結合齒輪-轉子系統模型，在考慮無載荷靜態傳動誤差的條件下，通過齒輪-轉子系統在不同修形曲線下的振動特性來驗證最佳修形的有效性，分析流程見圖1。

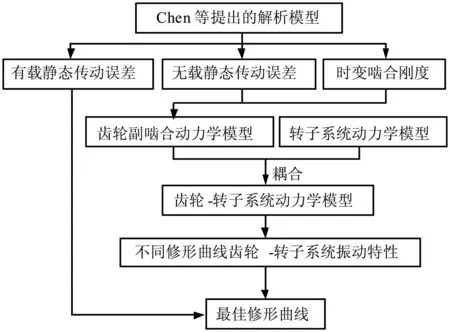
圖1　分析流程圖Fig.1 Flow chart of analysis

1考慮修形的輪齒嚙合剛度及靜態傳動誤差確定

1.1修形方法

齒廓修形有三種方式，齒頂修緣、齒根修緣及全齒廓修緣(齒頂和齒根同時修緣)，齒廓修形的設計包括確定修形長度、修形量和修形曲線。對輪齒進行齒根修緣，可以相當于對與之配對的輪齒進行齒頂修緣，因此齒頂修緣、齒根修緣及全齒廓修緣可達到同樣的修形效果，本文采用齒頂修緣(見圖2)。修形量用參數Cn表示，Cn=Ca/Ca_max，Ca為齒頂修形量，最大齒頂修形量Ca_max=0.02m，m為齒輪模數，修形長度用ΔLn表示，ΔLn=ΔLa/ΔLa_max,ΔLa為沿嚙合線方向的修形長度，ΔLa_max=0.6m。修形曲線方程一般為[10]

(1)

式中:x為以修形起點為坐標原點時嚙合線上任一位置的坐標，C為位置x處的修形量。本文選取三種修形曲線：n=1.5，n=2和漸開線，考慮齒頂修形方式，且修形長度ΔLa取各輪齒單雙齒嚙合區單側長度進行分析，確定不同修形量范圍內的最優修形曲線。

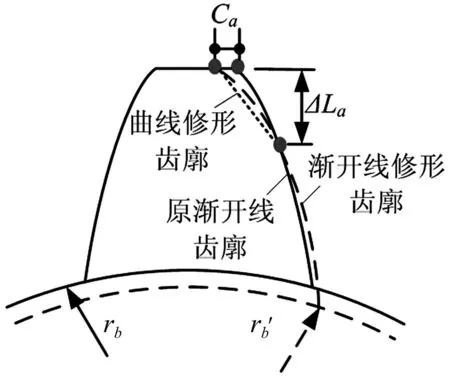
圖2　齒廓修形示意圖Fig.2 Schematic of gear tooth profile modification

1.2考慮修形的時變嚙合剛度和傳動誤差確定

齒輪參數見表1，假設扭矩T1=150 N·m，主動輪和從動輪的修形長度分別為各輪齒單雙齒嚙合區單側長度ΔLa1=1.595 mm，ΔLa2=1.546 mm，即ΔLn1=1.519，ΔLn2=1.472，在Chen等提出的解析模型基礎上，考慮基圓與齒根圓不重合[11]及真實過渡曲線[12]，針對表2所示的三種仿真工況，得到的三種工況下的時變嚙合剛度、有載荷和無載靜態傳動誤差(見圖3)。

表1　齒輪幾何參數

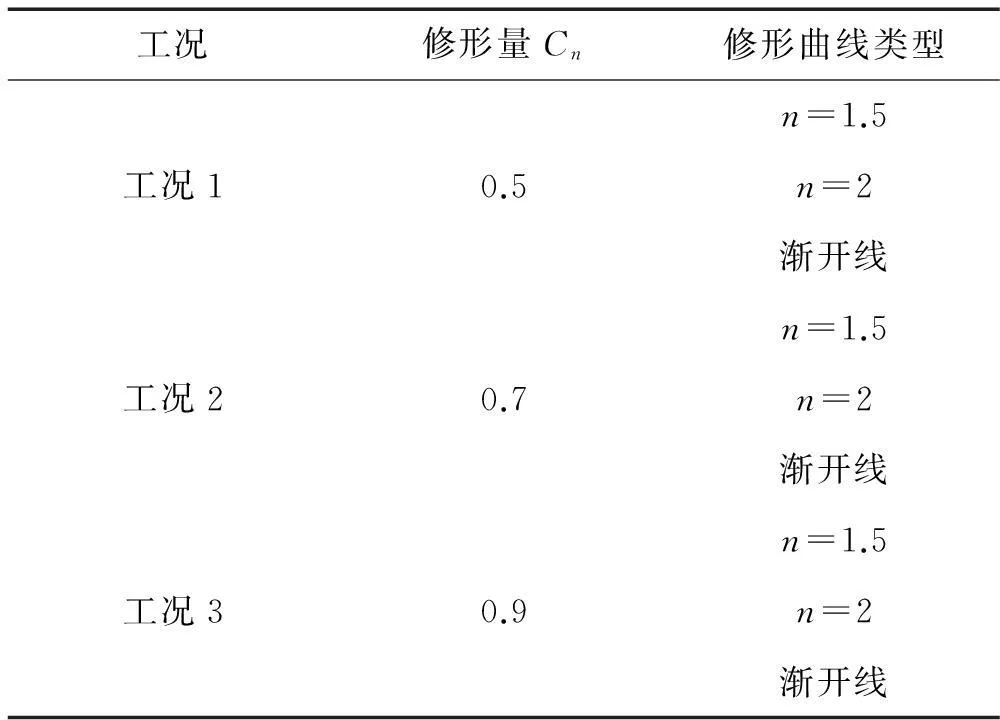
表2　仿真工況

由圖3可知，相同修形量的情況下3種修形方法對應的齒輪時變嚙合剛度幾乎完全相同，但有載荷靜態傳動誤差有所不同；采用同一修形方法不同修形量進行齒頂修形時，齒輪的重合度隨著修形量的增大而減小，有載荷靜態傳動誤差也有明顯的變化。由此可見，通過適當的修形可以降低有載荷靜態傳動誤差的波動。

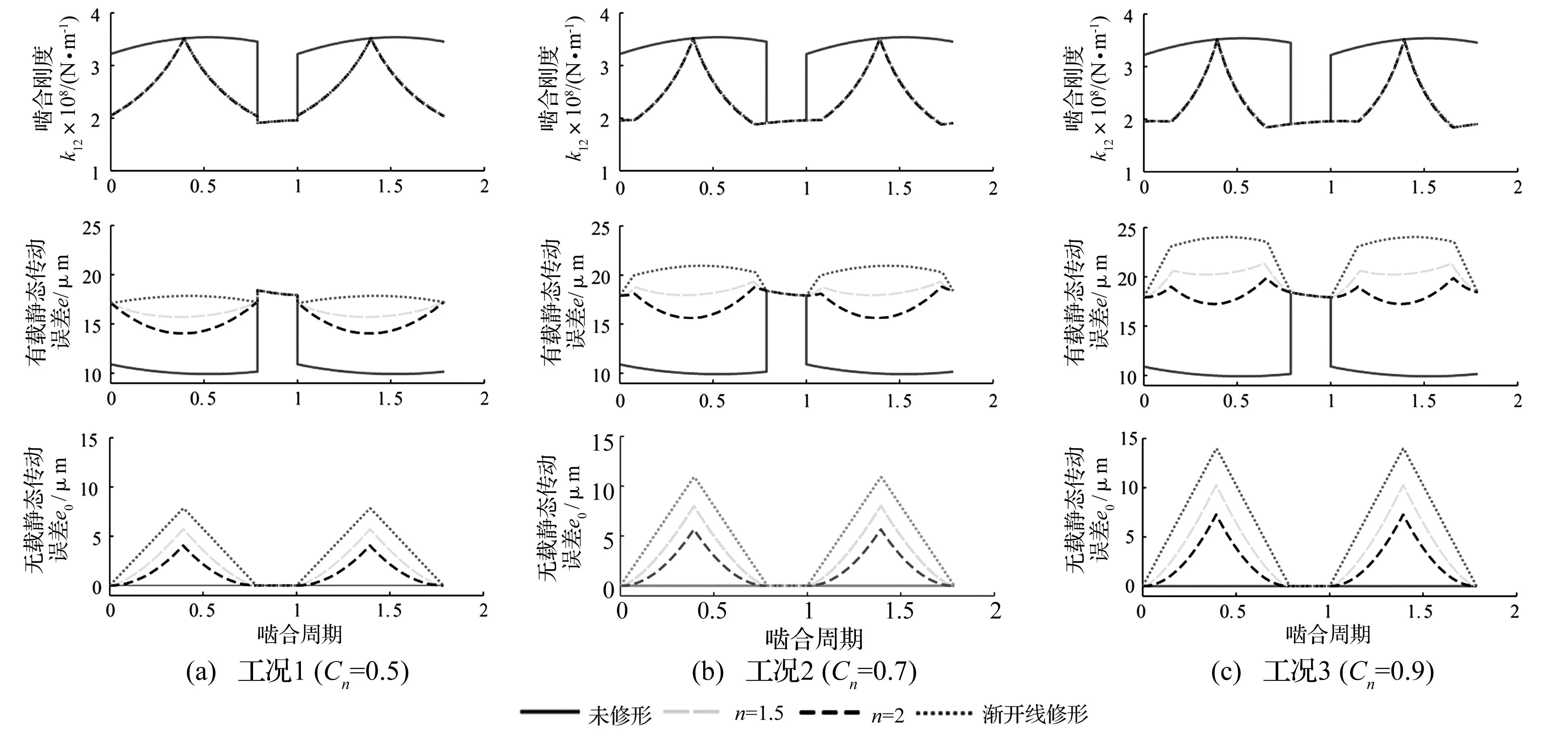
圖3　三種工況下的時變嚙合剛度和靜態傳動誤差Fig.3 TVMS and STE under three conditions

1.3不同修形方法下的最佳修形確定

靜態傳動誤差變化的相對峰峰值可用r來衡量，其表達式如下：

(2)

式中:pn和pm為未修形和修形情況下的有載荷靜態傳動誤差峰峰值。有載荷靜態傳動誤差變化幅度越小，即相對峰峰值r越小，修形效果越好。三種修形曲線，有載荷靜態傳動誤差相對峰峰值r隨修形量Cn的變化情況，見圖4，A、B兩點將修形量區間分為3部分，在區間[0,0.608]內，相同修形量下，漸開線修形獲得的有載荷靜態傳動誤差相對峰峰值r變化最小，修形效果最佳；在區間[0.608,0.837]內，曲線n=1.5的修形效果最佳；當Cn大于0.837時，曲線n=2的修形效果最佳。因此在修形量確定的情況下，可根據該圖選擇修形曲線，以達到最佳修形效果，但值得注意的是修形量Cn過大，重合度會降低過多，會導致齒輪運轉平穩性降低，引起振動和噪聲，反而達不到修形的作用。因此應根據實際情況，確定適當的修形量，進而選擇最佳修形曲線進行修形。

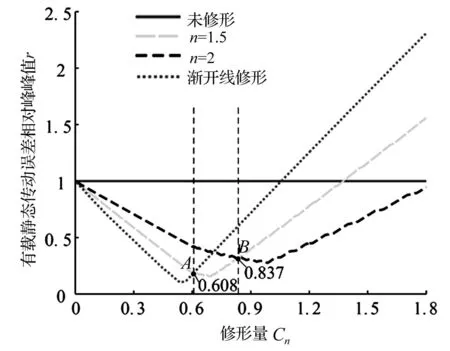
圖4　不同修形量下的有載荷靜態傳動誤差相對峰峰值Fig.4 Relative peak-peak value of loaded STE under different amounts of profile modification

2考慮齒輪-轉子系統振動特性的最佳修形

僅利用有載荷靜態傳動誤差相對變化來確定最佳修形曲線，不能反映修形對齒輪動態特性的影響，此外利用齒輪-轉子系統的動態響應來反映系統的振動特性更具現實意義，因此本節將采用修形后齒輪-轉子系統的振動特性，來驗證最佳修形曲線的選取。

2.1齒輪-轉子系統模型建立

將齒輪視為通過彈簧和阻尼器連接的剛性圓盤，其嚙合動力學模型見圖5，O1，O2為齒輪中心，Ω1、Ω2為齒輪轉動角速度，取逆時針為正，順時針為負；rb1、rb2為齒輪基圓半徑；齒輪時變嚙合剛度和阻尼分別用k12(t)和c12(t)(本文c12(t)=0)表示；定義y軸正向與嚙合面的夾角為：

(3)

式中:α為齒輪壓力角，α12(0≤α12≤ 2π)為主動輪的x軸逆時針旋轉至中心線的夾角。

為了考慮主動輪轉動方向的影響，引入σ函數：

(4)

設兩齒輪在嚙合線方向上的相對位移為p12(t)，則

p12(t)=(-x1sinψ12+x2sinψ12+y1cosψ12-

y2cosψ12+σ×rb1θz1+σ×rb2θz2)-e12(t)

(5)

式中:e12(t)為靜態傳動誤差，本文僅考慮由于修形引起的齒廓誤差，即無載荷靜態傳動誤差e0(t)。

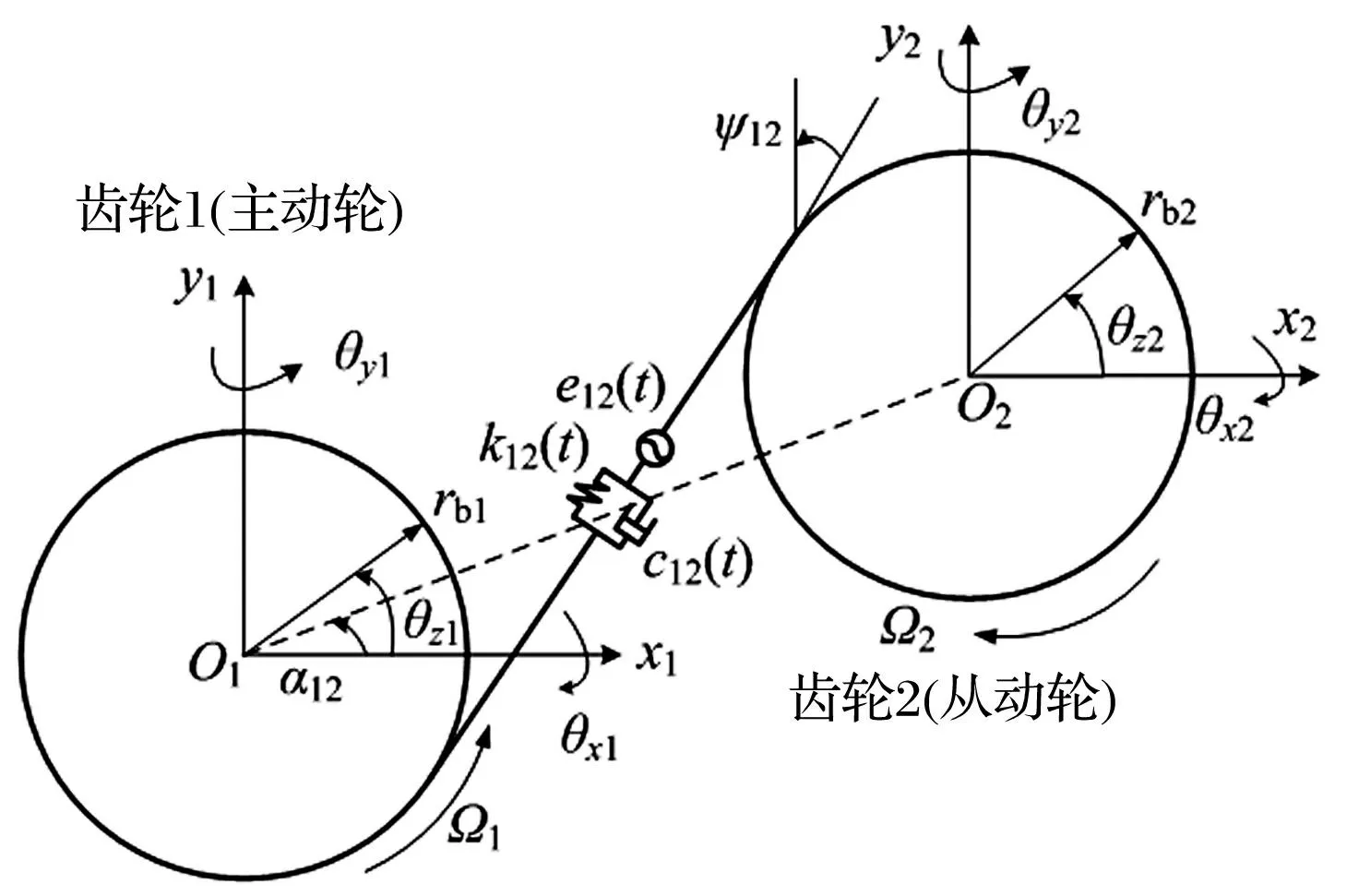
圖5　齒輪副嚙合動力學模型Fig.5 Dynamic model of gear pair

不考慮齒側間隙、嚙合摩擦力等的影響，分別建立齒輪在六個自由度方向的運動方程：

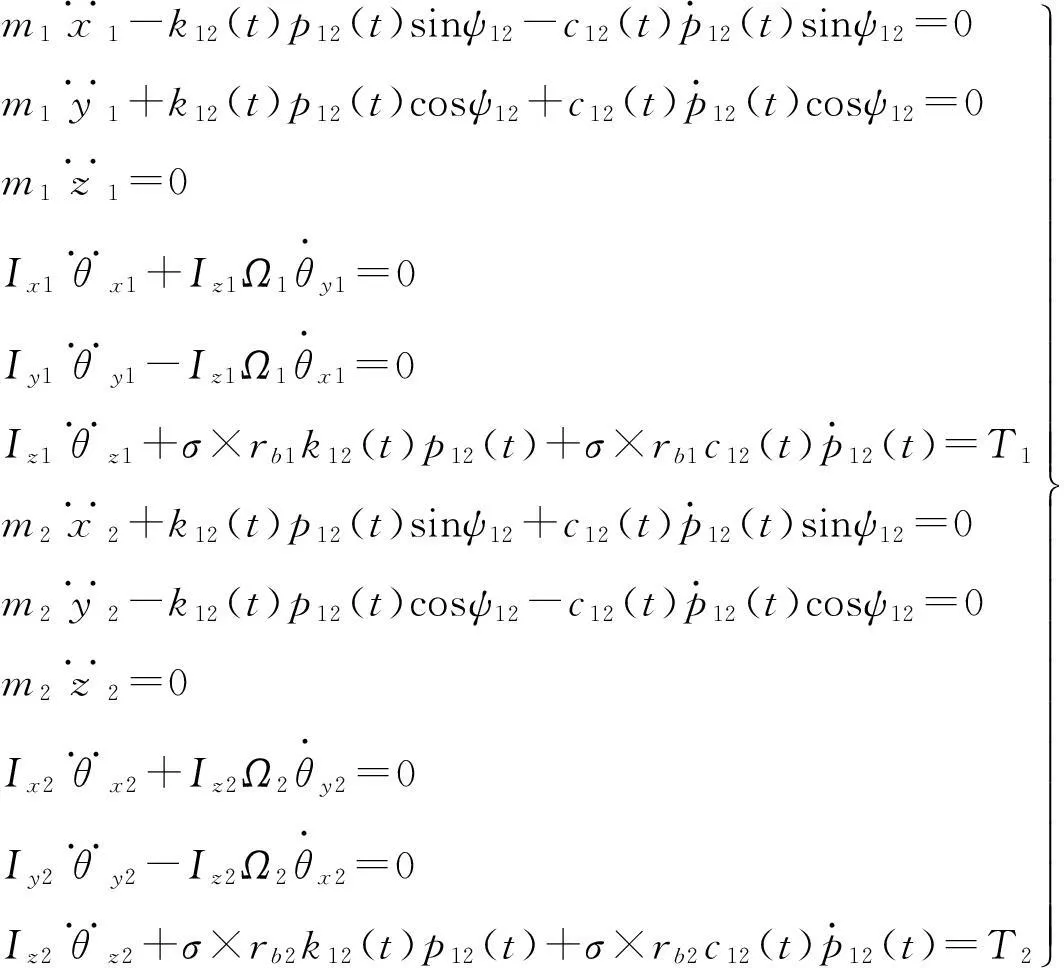
式中:m1、m2為齒輪1、齒輪2的質量，Ix1、Iy1、Iz1、Ix2、Iy2、Iz2分別為齒輪1和齒輪2繞x軸、y軸和z軸的轉動慣量，T1為施加在主動輪扭矩，T2為負載扭矩。

將其簡化成矩陣形式，得到齒輪副運動耦合方程為：

(7)

式中:X12為齒輪副質心的廣義坐標，M12為齒輪副的質量矩陣，K12為嚙合剛度矩陣，C12為嚙合阻尼矩陣，G12為陀螺矩陣。

將齒輪嚙合動力學模型和轉子系統模型進行耦合，得到如圖6所示的齒輪-轉子系統有限元模型。系統的運動方程可表示為：

(8)

式中:M為系統質量矩陣，包含轉軸質量、齒輪質量以及集中質量；G為陀螺力矩；C為系統阻尼矩陣，采用粘性阻尼；K為系統剛度矩陣，包括轉軸剛度、齒輪嚙合剛度以及軸承剛度。u為系統廣義坐標，Fu為激振力矢量。

圖6　齒輪-轉子系統有限元模型Fig.6 Finite element model of a gear-rotor system

2.2考慮不同輪齒修形的系統振動特性分析

本節將分析表2所示的3種工況下齒輪-轉子系統的振動響應。工況1 (Cn=0.5)齒輪1處x方向位移和齒輪嚙合力均方根隨嚙合頻率的變化曲線見圖7，由圖7(a)可知，未修形時，當嚙合頻率ω12分別等于系統的固有頻率ω1、ω3、ω7、ω9，ω1/n(n=6,5,4,3,2)和ω7/2時位移響應出現共振峰，修形后ω7/2處的共振峰消失，并且位移響應幅值明顯降低。當嚙合頻率大于150 Hz時，位移響應均方根值由大到小依次為未修形、曲線n=2修形、曲線n=1.5修形和漸開線修形，即漸開線修形效果最佳，與圖4中修形量Cn=0.5時靜態傳動誤差相對峰峰值大小順序所對應修形曲線一致，說明了靜態傳動誤差相對峰峰值越小，修形效果越好；當嚙合頻率低于150 Hz時，在嚙合頻率等于ω1/3處，曲線n=2修形對應的幅值最低；在嚙合頻率等于ω1/4處，曲線n=1.5修形對應的幅值最低。因此，嚙合頻率較低時，僅根據有載荷靜態傳動誤差選取最佳修形曲線是不夠的，需根據齒輪的工作轉速，結合齒輪振動特性選取修形曲線。由圖7(b)可知，修形后嚙合力幅值顯著降低，并且漸開線修形對應的嚙合力變化最為平緩。

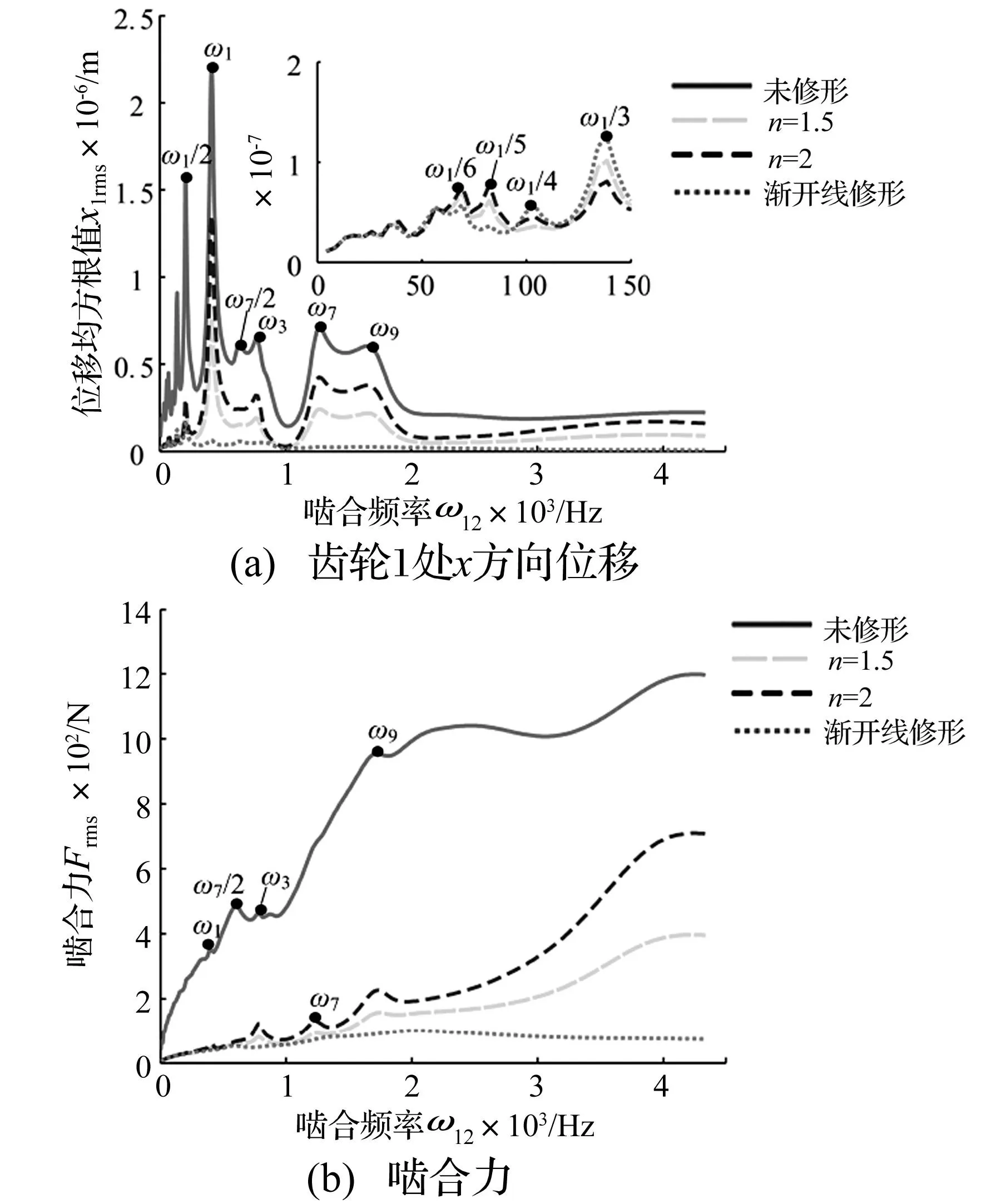
圖7　齒輪1處x方向位移和嚙合力均方根變化曲線(Cn=0.5)Fig.7 Root-mean-square of displacement in the xdirection of gear 1 and gear mesh force (Cn=0.5)

齒輪1處x方向振動加速度隨時間變化曲線見圖8，從圖中可以看出修形后齒輪的振動加速度幅值顯著降低。

當嚙合頻率高于2 600 Hz時，振動響應的變化十分平緩(圖7)，因而對于工況2和工況3只分析轉速在0～2 600 Hz范圍內的振動特性。圖9為工況2 (Cn=0.7)齒輪1處x方向位移均方根值隨嚙合頻率的變化曲線，嚙合頻率較高時，n=1.5修形曲線修形效果最佳，而漸開線和n=2修形曲線的修形效果幾乎相同，規律與圖4有載荷靜態傳動誤差相對峰峰值變化規律相同；嚙合頻率較低時，漸開線修形效果最差。圖10為工況3 (Cn=0.9)齒輪1處x方向位移均方根值隨嚙合頻率的變化曲線，嚙合頻率較高時，n=2修形曲線修形效果最佳，其次是n=1.5修形曲線，漸開線修形效果最差，規律與圖4有載荷靜態傳動誤差相對峰峰值變化規律相同；嚙合頻率較低時，漸開線修形效果仍為最差。

圖8 齒輪1處x方向加速度響應曲線(Cn=0.5)Fig.8Accelerationresponsesofgear1inxdirection(Cn=0.5)圖9 齒輪1處x方向位移均方根值(Cn=0.7)Fig.9Root-mean-squareofdisplacementinthexdirectionofgear1(Cn=0.7)圖10 齒輪1處x方向位移均方根值(Cn=0.9)Fig.10Root-mean-squareofdisplacementinthexdirectionofgear1(Cn=0.9)

3結論

(1)由于齒輪有載荷靜態傳動誤差峰峰值相對變化越小，修形效果越好，本文通過對比三種修形曲線在不同修形量下對應有載荷靜態傳動誤差峰峰值，獲得了不同修形量對應的最佳修形曲線。

(2)由于有載荷靜態傳動誤差不能反映齒輪的動態特性，本文通過齒輪-轉子系統的動態特性進一步確定最佳修形曲線，發現高頻情況下通過齒輪-轉子系統動態特性確定的最佳修形曲線與根據有載荷靜態傳動誤差峰峰值確定的最佳修形曲線相同，但在低頻情況下，二者有所差別。根據扭矩、修形曲線、修形長度，可獲得不同修形量下有載荷靜態傳動誤差峰峰值，高頻時可通過比較有載荷靜態傳動誤差峰峰值確定最佳修形曲線，低頻時需根據齒輪-轉子系統振動特性確定最佳修形曲線。

參考文獻

[1]朱孝錄．齒輪傳動設計手冊[M]．北京：化學工業出版社，2005．

[2]Ohno K，Tanaka N．Contact stress analysis for helical gear with 3-dimensional finite element method[J]．Transactions of the Japan Society of Mechanical Engineers．C，1998，64：4821-4826．

[3]Wagaj P，Kahraman A．Impact of tooth profile modification on the transmission error excitation of helical gear pairs[C]．Proceedings of ESDA2002：6th Biennial Conference on Engineering Systems Design and Analysis， Istanbul，Turkey，2002:8-11．

[4]Li S T．Effects of machining errors，assembly errors and tooth modifications on loading capacity, load-sharing ratio and transmission error of a pair of spur gears[J]．Mechanism and Machine Theory，2007，42(6)：698-726．

[5]Tharmakulasingam R，Alfano G， Atherton M．Reduction of gear pair transmission error with tooth profile modification[C]．ISMA 2008, International Conference on Noise and Vibration Engineering，Leuven，Belgium，2008:15-19．

[6]Tesfahunegn Y A，Rosa F，Gorla C．The effects of the shape of tooth profile modification on the transmission error，bending，and contact stress of spur gears[J]．Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2010，224(8)：1749-1758．

[7]Tavakoli M S，Houser D R．Optimum profile modifications for the minimization of static transmission errors of spur gears[J]．ASME Journal of Mechanism, Transmissions and Automation in Design，1986，108(3)： 86-95．

[8]Ma H, Yang J, Song R Z, et al. Effects of tip relief on vibration responses of a geared rotor system, proceedings of the institution of mechanical engineers, part c[J].Journal of Mechanical Engineering Science，2014，228(7)：1132-1154.

[9]Chen Z G，Shao Y M．Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]．Mechanism and Machine Theory，2013，62：63-74．

[10]李潤方，王建軍．齒輪系統動力學-振動、沖擊、噪聲[M]．北京：科學出版社，1997．

[11]萬志國，訾艷陽，曹宏瑞，等．時變嚙合剛度算法修正與齒根裂紋動力學建模[J]．機械工程學報，2013, 49(11)：153-160．

WAN Zhi-guo，ZI Yan-yang，CAO Hong-rui，et al．Time-varying mesh stiffness algorithm correction and tooth crack dynamic modeling[J]．Journal of Mechanical Engineering，2013，49(11)：153-160．

[12]郭忠，張艷冬．基于APDL的漸開線直齒圓柱齒輪參數化精確建模[J]．機械制造與研究，2010，39(3)：33-36．

GUO Zhong，ZHANG Yan-dong．Parameterization precise modeling of involutes spur gear based on APDL [J]．Machinery Manufacturing and Research，2010，39(3)：33-36．