具有角度穩定性的頻率選擇表面?

(山東理工大學電氣與電子工程學院,山東淄博255049)

0 引言

頻率選擇表面(FSS)是一種新型的人工電磁材料,當投射電磁波與其相互作用時會顯現出帶通或帶阻的濾波特性,類似一種空間濾波器的功能[1-4]。通常FSS是一種二維的表面周期陣列,有貼片型(周期性排布的金屬貼片)或孔徑型(金屬屏上周期性的開孔)兩種類型。FSS可方便地通過人為調整設計參數來調整其頻率特性,因此FSS的應用幾乎涉及到整個電磁頻譜,從可見光頻譜范圍直到微波頻譜范圍都成為研究熱點[5-9]。

FSS結構為多參數設計,僅表面屏本身而言,就有諧振周期圖案選形、周期圖案的排列布局及襯底電介質的電性能參數等。FSS主要頻率響應特性指標有諧振頻率、諧頻處的透過率、帶寬等。同時,考慮投射到表面屏上的電磁波,投射角度和投射電磁波的偏振方式成為不可忽略的重要影響因素。FSS的實際工程應用環境中,要選用偏振穩定性好的周期單元,并且很多時候投射電磁波的投射角度涉及到大的入射范圍,此時要得到優良的濾波性能指標,往往同時選用角度穩定性能較好的圖形單元,才有可能得到高性能的濾波器。

常用正方形柵格排布的十字周期圖案FSS,結構是對稱的,因此具有正入射時的偏振穩定性,應用比較多。但是當投射電磁波的投射角度發生改變時,其諧振頻率卻表現出很大的漂移,頻率的漂移極大地降低了FSS的性能。對此問題人們一直以來都在尋求可行的解決方法:侯新宇等通過優選圖形周期圖案——Y孔周期圖案的方法來實現FSS對投射角度的穩定性[10];Munk等則是采用加載電介質的方式改善大角度投射時FSS的傳輸特性[1];賈宏燕等采用密集型周期圖案排布的方法來獲得大角度下FSS的穩定頻率響應特性[11]。但是上述幾種解決方法也同時存在一定的缺陷:Y形周期圖案偏振穩定性不好[12];加載電介質又往往會增加傳輸損耗[13];密集型排布的周期圖案會使得濾波帶寬加寬影響濾波性能。

本文提出一種簡單有效的新方法。以常用的正方形柵格排布的十字周期圖案FSS為基礎,把每個十字周期圖案旋轉45°疊加在原來的十字周期圖案上,給出了一種優化的新型周期圖案FSS設計。這種優化的FSS結構能夠實現對不同投射角度中心頻率的穩定性。為了進行對比分析,分別對常用的十字周期圖案FSS結構和新周期圖案FSS結構,利用模式匹配法進行了理論分析,同時制作了實驗樣件,在實驗室中進行測試。

1 理論分析

采用模式匹配法分別對常用十字周期圖案FSS和優化的新周期圖案FSS結構進行分析。在頻率選擇表面兩側的自由空間,電磁場都可以用Floquet諧波模式進行展開,繼而在FSS屏表面應用橫向場連續的電磁邊界條件,即可列出關于頻率選擇表面孔徑周期圖案的待求電場的積分方程,具體如下式所示。

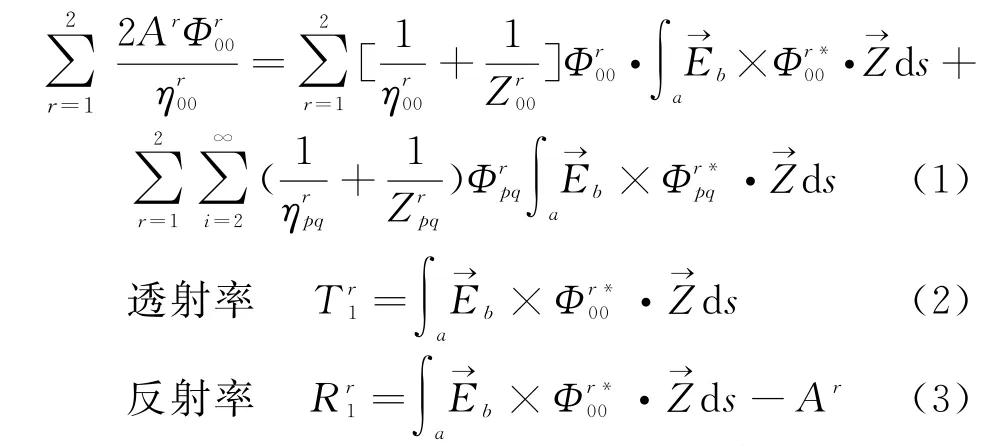
式中:A r為電磁投射波的振幅值,→E b為待求的孔徑電場為Floquet完備正交的諧波模式,當p和q取0值時,i為1,此時對應的模式為平面波模式,p,q不同為零值時,i≥2,此時對應其他的模式;r為不同的偏振方式,r=1,2分別代表TE和TM波;“?”為復共軛為等效模阻抗,p和q值決定任意i階Floquet模,并且

2 數值結果與分析

2.1 常用和改進十字周期圖案FSS的設計結構

Munk在FSS的研究中指出,對于十字形的諧振周期圖案,諧振現象出現在周長類比諧振波長時[1]。因此我們可以依照這個判據進行十字周期圖案的參數設計,詳細參數標注如圖1所示。

常用正方形柵格排布的十字周期圖案FSS有一個明顯的特點,每個十字周期圖案取向都是相同的,圖2給出了常用十字周期圖案FSS陣列圖。在常用十字周期圖案FSS的基礎上,把每個十字周期圖案旋轉45°疊加在原來的十字周期圖案上,給出一種優化的新型周期圖案FSS,如圖3所示。

圖3 改進的十字單元FSS

常用FSS周期陣列圖參數設置:陣列周期D x=D y=16 mm,臂寬w=0.5 mm,臂長L=15 mm。投射波均取45°投射角,選取頻段為6～11 GHz。為了進行進一步的對比分析,圖3所示的改進FSS結構,選取頻段為5～9.5 GHz,其他參數設置相同。

下面分別對常用十字周期圖案FSS結構和優化的FSS結構進行兩個方面的對比研究:1)在一定入射角度下,不同偏振方式電磁波投射時陣列的頻率響應特性;2)在一定的偏振情況下,對不同投射角度的電磁波FSS陣列中心頻率的變化規律。

2.2 不同偏振方式對兩種FSS頻率響應特性的影響

TE,TM兩種不同偏振方式的波源垂直投射時,由于周期陣列與其旋轉90°后對稱,傳統和優化的正方形柵格十字周期圖案FSS的傳輸特性均不受垂直入射源偏振的約束,具有較好的偏振穩定性。在大角度入射時,選取45°角入射為例,給出了兩種FSS結構的頻率響應曲線,如圖4和圖5所示。圖4表明常用FSS結構在TE偏振45°角入射的電磁波投射時,中心頻率為9.8 GHz,當TM偏振45°角入射的電磁波投射時,中心頻率向低頻漂移到了9 GHz,中心頻率漂移為0.8 GHz。對于改進的FSS結構,圖5表明優化的FSS結構在TE偏振45°角入射的電磁波投射時,中心頻率為8.9 GHz,當偏振方式為TM時,中心頻率同樣向著低頻方向漂移為8.5 GHz,但是漂移量與傳統FSS結構相比要小,為0.4 GHz,為傳統FSS結構漂移量的一半。改進的FSS結構比傳統FSS具有更好的極化穩定性。

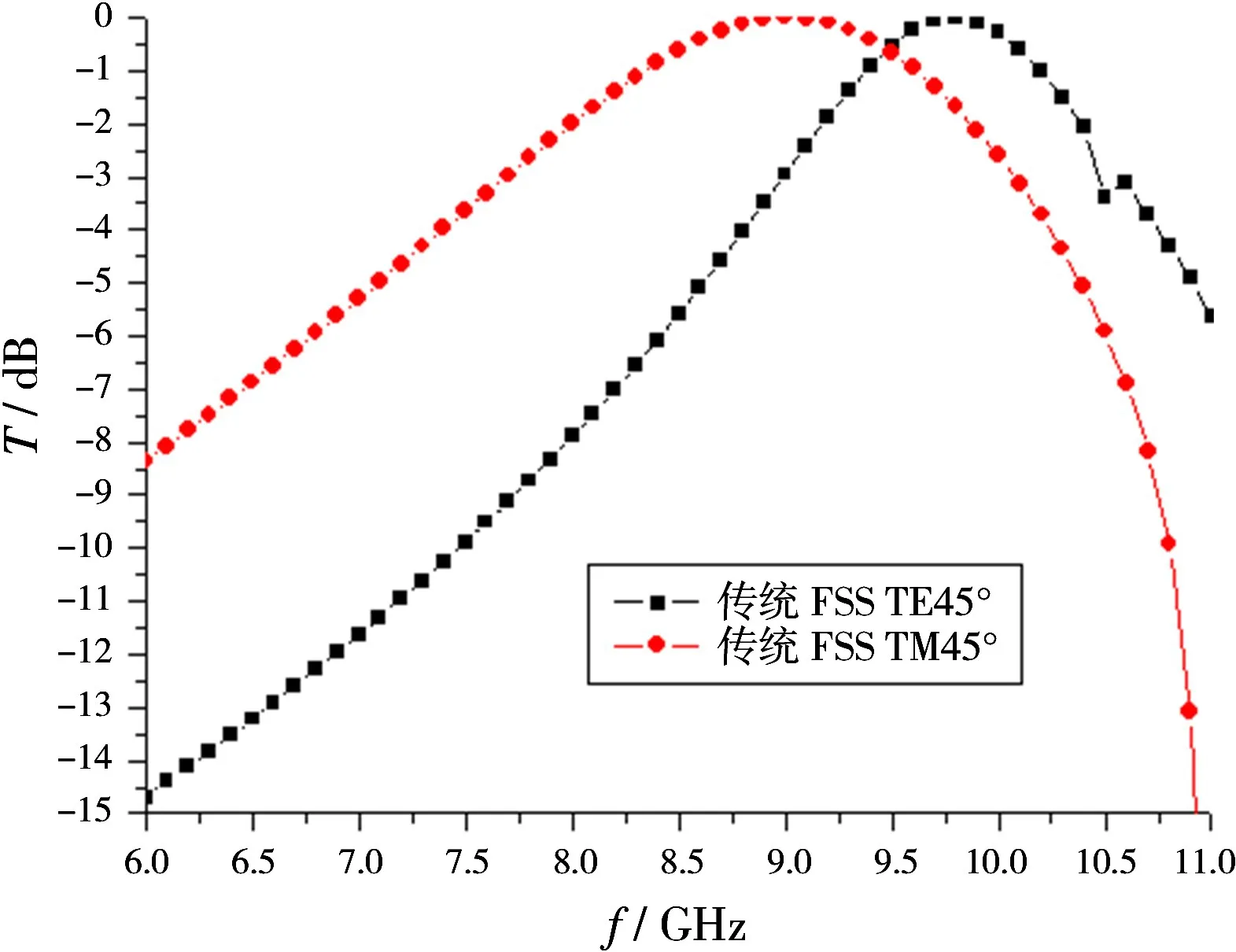
圖4 傳統十字單元FSS不同極化方式的頻率響應

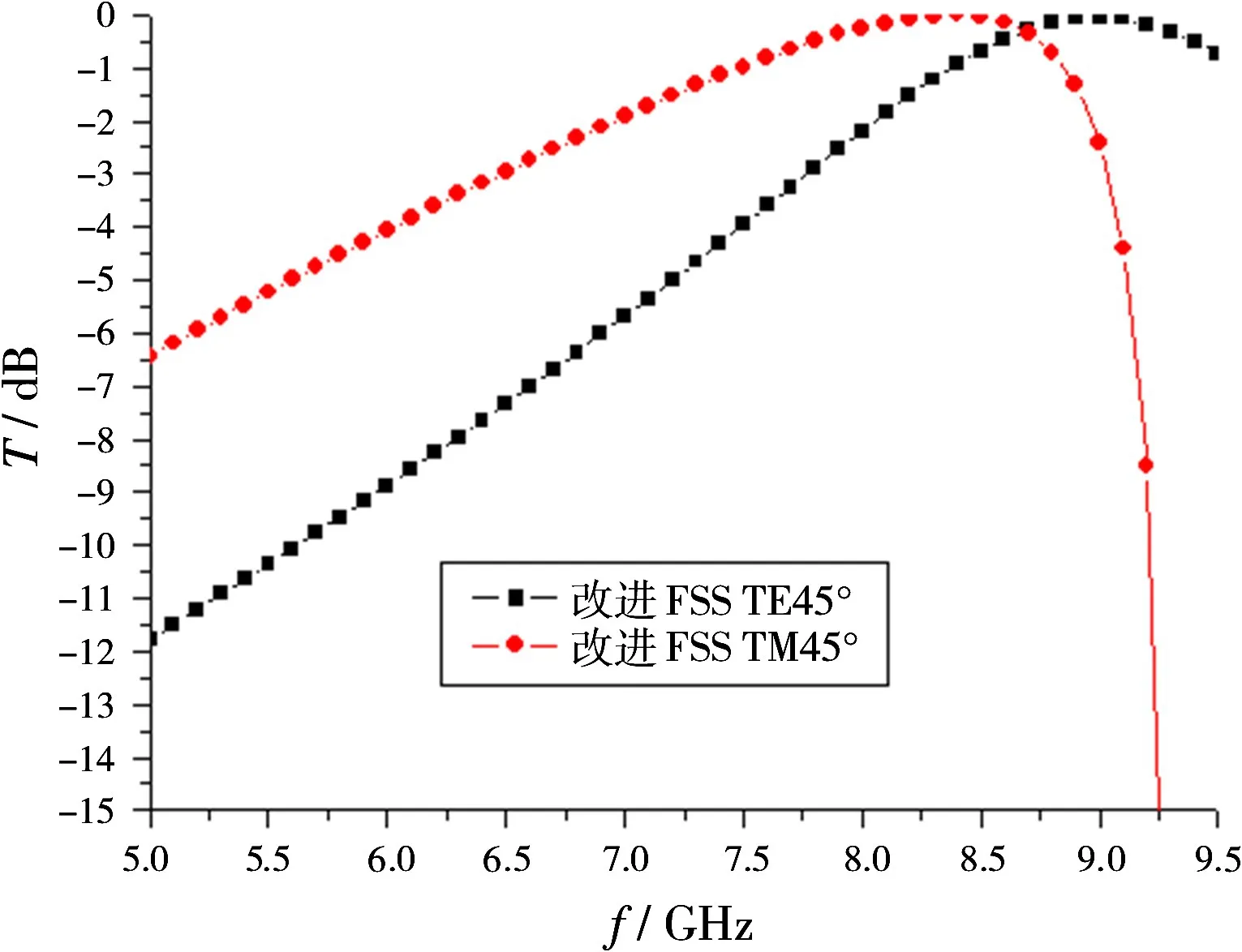
圖5 改進FSS結構不同極化方式的頻率響應

2.3 不同投射角度對兩種FSS頻率響應特性的影響

FSS工程應用中經常涉及到不同角度投射的情況,在考慮選取偏振穩定性能較好的對稱單元的同時,必須考察FSS的中心頻率對不同投射角度的穩定性。下面針對上述兩種FSS結構,分別計算出正投射時的中心頻率,然后改變投射角度,得出不同投射角度下原中心頻率處的透過率系數,由中心頻率處透過率的變化可以得出中心頻率的角度穩定性。正投射時中心頻率分別為9.5 GHz和9.2 GHz。以TE偏振方式為例,選取角度變化范圍為1°到45°角度,步長為4°。計算結果如圖6所示。

由圖6給出的數據可以很明顯地看出,對于常用十字周期圖案FSS結構,投射波的投射角度由正投射逐漸變化到45°投射時,中心頻率點的透過率隨投射波角度的變大而降低:正投射時透過率為-0.001 7 dB,45°投射時變為-0.624 dB。中心頻率點的透過率降低是由于中心頻率隨投射角度變化發生了漂移。這在很多涉及到大角度范圍應用的情況,降低了FSS性能從而限制了FSS的應用。相比較而言,對于優化的FSS結構,投射角度由正投射逐漸變化到45°時,中心頻率透過率幾乎不發生改變:正投射時為-0.008 8 d B,45°投射時為-0.194 dB。

通過計算可以看出常用FSS結構的頻率響應雖然能具備正入射時的偏振穩定性,但是當投射波投射角度改變時,中心頻率的透過率有很大的下降;而對于改進結構的FSS具有更優的傳輸特性,在具有較好的偏振穩定性能的同時,能夠對于不同的投射角度得到較穩定的中心頻率。

3 實驗測試

目前FSS的工藝制備有很多新方法[14],本設計僅對研究平面型的FSS結構,因此可采用鍍膜和光刻的方法制備FSS測試樣件[15],尺寸為300 mm×300 mm,此時等效認為是無限周期的FSS。在實驗室中對兩種實驗樣件進行偏振穩定性和角度穩定性兩方面的實驗測試,以驗證理論計算結果。

投射電磁波在不同的偏振方式時,測試FSS設計屏的偏振穩定性。實際測試中,TE波與TM波的不同偏振方式的轉換,可以旋轉FSS表面屏90°來實現,而不需要像常規測試中調整發射設備。常用和優化的FSS結構的實驗樣件測試結果如圖4、圖5所示,測試值和理論計算值基本一致。對兩種FSS結構中心頻率的角度穩定性進行測試時,選定TE極化方式,轉動測試件轉臺,使投射角度由正投射逐漸增大到45°投射,旋轉角度間隔取為4°。測試值和測試照片分別如圖6和圖7所示,測試結果驗證了理論值的正確性。

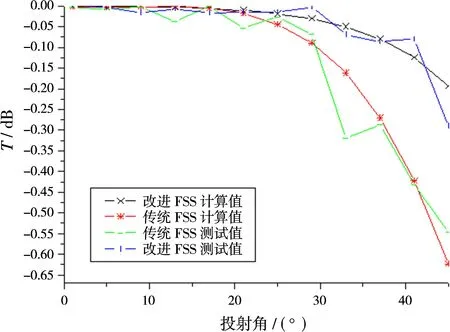
圖6 兩種FSS結構中心頻率透過率隨入射角度的變化

圖7 FSS測試系統

4 結束語

投射波的投射角度一直是影響FSS傳輸特性的一個重要因素。本文選取正方形柵格十字周期圖案FSS結構為基礎進行改進,設計了由十字周期圖案旋轉45°疊加得到的一種新型周期圖案頻率選擇表面。計算和測試結果均表明:常用的十字周期圖案FSS具備正入射時的偏振穩定性,但是當波源的投射角改變時,FSS中心頻率處傳輸損耗會很大,而優化的FSS結構在大角度入射時具有更好的偏振性能,且能夠實現中心頻率對投射角度的穩定性。它可以為很多涉及到曲面大范圍角度投射的情況提供一定的設計思路,如衛星通信領域及隱身曲面雷達罩的設計。

[1]MUNK B A.Frequency Selective Surface:Theory and Design[M].New York:Wiley,2000.

[2]WU T K.Frequency Selective Surface and Grid Array[M].New York:Wiley,1995.

[3]YU Miao,XU Nianxi,GAO Jinsong.Infrared Transparent Frequency Selective Surface Based on Iterative Metallic Meshes[J].Chinese Physics B,2015,24(3):107-110.

[4]路寶,龔書喜,凌勁,等.一種新型頻率選擇表面及其在天線雷達散射截面減縮中的應用[J].電子與信息學報,2010,32(1):199-202.LU Bao,GONG Shuxi,LING Jin,et al.A Novel Frequency Selective Surface Structure and Its Application to RCS Reduction of Antennas[J].Journal of Electronics&Information Technology,2010,32(1):199-202.(in Chinese)

[5]劉曉春,張文武,孫世寧.頻選雷達罩電性能的基本問題及解決方法[J].雷達科學與技術,2012,10(3):336-340.LIU Xiaochun,ZHANG Wenwu,SUN Shining.Elementary Problems and Solutions for Electrical Performance Design of FSS Radome[J].Radar Science and Technology,2012,10(3):336-340.(in Chinese)

[6]王新彪,李靖,張升偉.毫米波/亞毫米波臨邊探測儀準光技術[J].太赫茲科學與電子信息學報,2013,11(4):595-600.WANG Xinbiao,LI Jing,ZHANG Shengwei.Quasi-Optical Technology in Millimeter/Sub-Millimeter Limb Sounder[J].Journal of Terahertz Science and Electronic Information Technology,2013,11(4):595-600.(in Chinese)

[7]張建,高勁松,徐念喜.光學透明頻率選擇表面的設計研究[J].物理學報,2013,62(14):1-7.ZHANG Jian,GAO Jinsong,XU Nianxi.Design and Study of Optically Transparent Band-Pass Frequency Selective Surface[J].Acta Physica Sinica,2013,62(14):1-7.(in Chinese)

[8]張建,高勁松,徐念喜,等.基于混合周期柵網結構的頻率選擇表面設計研究[J].物理學報,2015,64(6):326-332.

[9]陳亮,陳夏萌,陳強,等.基于非諧振單元的小型化帶通頻率選擇表面設計[J].中國艦船研究,2015,10(2):84-88.CHEN Liang,CHEN Xiameng,CHEN Qiang,et al.Design of Bandpass Miniaturized Frequency Selective Surfaces Composed of Non-Resonant Elements[J].Chinese Journal of Ship Research,2015,10(2):84-88.(in Chinese)

[10]侯新宇,張澎,盧俊,等.一種雙曲率雷達罩的頻率選擇表面分片設計[J].彈箭與制導學報,2006,26(1):123-125.HOU Xinyu,ZHANG Peng,LU Jun,et al.A Novel Frequency Selective Surfaces Patch Design for Double Curved Radome[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(1):123-125.(in Chinese)

[11]JIA Hongyan,GAO Jinsong,FENG Xiaoguo.Closely Packed Dense Frequency Selective Surface[J].Chinese Optics Letters,2008,6(6):441-442.

[12]盧俊,張靚,孫連春.Y形和Y環形單元特性的實驗對比研究[J].光學精密工程,2005,13(2):219-224.LU Jun,ZHANG Jing,SUN Lianchun.Experimental Comparison of the Characteristics of Y Element and Y Loop Element[J].Optics and Precision Engineering,2005,13(2):219-224.(in Chinese)

[13]侯新宇,萬偉,佟明安,等.介質損耗對頻率選擇表面傳輸特性的影響[J].電子科學學刊,2000,22(5):871-874.

[14]高勁松.基于立體打印技術制作曲面頻率選擇表面[J].實驗室研究與探索,2015,34(3):4-7.

[15]龐玉蓮,鄒應全.光刻材料的發展及應用[J].信息記錄材料,2015,16(1):36-51.