裂尖具線性分布約束應力的運動裂紋模型及其解析解

2015-12-30 03:19:47唐雪松,陳旻煒,高常輝

振動與沖擊 2015年3期

第一作者唐雪松男，教授，博士，1964年生

唐雪松，陳旻煒，高常輝

(長沙理工大學土木與建筑學院力學系，長沙410114)

摘要：以恒定速度運動的Griffith裂紋解析解為著名的Yoffe解。靜止裂紋的條狀屈服模型即Dugdale模型，將其推廣到運動裂紋模型時發現，當裂紋運動速度跨越Rayliegh波速時，裂紋張開位移COD趨于∞，且表現為間斷。通過在裂尖引入一個約束應力區及兩個速度效應函數，假設約束應力為線性分布，采用復變函數方法，求得動態應力強度因子SIF與裂紋張開位移COD的解析解。新的結果，在Rayleigh波速下裂紋張開位移連續且為有限值。給出裂紋張開位移的一些數值結果，獲得了一些有意義的結論。

關鍵詞：運動裂紋；Ⅰ型裂紋；約束應力；復變函數方法；應力強度因子SIF；裂紋張開位移COD

基金項目：973項目資助(2015CB057705);國家自然科學基金資助(51378081)

收稿日期：2013-09-30修改稿收到日期：2014-02-14

中圖分類號:O346.1文獻標志碼：A

A model of moving crack with a linear distribution of restraining stresses in crack tip zone

TANGXue-song,CHENMin-wei,GAOChang-hui(Department of Mechanics, School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410114, China)

Abstract:The analytical solution of moving Griffith crack model with a constant speed is well known as Yoffe solution. For a static crack, its strip yielding model is well known as Dugdale model. It is found that when Dugdale model is generalized to the moving crack case, the crack opening displacement (COD) is discontinuous and approaches to positive and negative infinite at Rayleigh wave speed. Here, a restraining stress zone was attached to the crack tip while two speed effect functions were introduced assuming the restraining stress zone has a linear distribution. The complex function approach was employed to solve the problem. Analytical solutions of dynamic stress intensity factor (SIF) and crack opening displacement (COD) were then obtained. The new COD result was continuous and finite at Rayleigh wave speed. Some numerical results of COD were presented. Some valuable conclusions were obtained.

Key words:moving crack; model I crack; restraining stress; complex function approach; stress intensity factor (SIF); crack opening displacement (COD)

關于運動裂紋的研究與求解，不但具有重要學術意義，還具有一定實用參考價值。若僅考察運動裂紋尖端，可一定程度反映動態裂紋擴展的一些力學行為。Yoffe[1]最早獲得了以恒定速度運動的Griffith裂紋模型的解析解，即著名的Yoffe解。關于運動裂紋的研究仍然是當前國際上的熱點研究問題。近期的一些研究成果包括：電磁彈性材料反平面剪切下運動裂紋問題的研究[2]，壓電雙材料中含接觸區的界面運動裂紋的研究[3]，壓電雙材料含有限穿透裂紋沿界面運動問題的研究[4]，電磁彈性矩形板中運動裂紋問題的研究[5]，正交各向異性雙材料中界面裂紋附近螺型運動位錯的研究[6]，微觀、細觀與宏觀尺度下裂紋尺寸與速度相互影響的研究[7]，宏觀主裂紋運動速度接近剪切波速時微觀裂尖鈍化效應的研究[8]等。國內近期研究成果包括，關于宏微觀雙尺度運動裂紋解析求解的研究[9]，對Ⅲ型運動裂紋均布載荷與集中載荷作用下的斷裂動力學問題的研究[10]，對黏結于均勻材料基底上功能梯度材料涂層平面運動裂紋問題的研究[11]，對功能梯度壓電板條中電絕緣型運動裂紋電彈性場的研究[12]，對不同壓電介質界面上的反平面運動裂紋的研究[13]，等。

由于數學上的限制，對運動裂紋問題一般限制速度在Rayleigh波速以下。實際上，裂紋運動速度不但可達到Rayleigh波速，還可超過剪切波速[14]。本文在運動裂紋尖端引入一個約束應力區，約束應力大小、分布與裂尖材料的損傷程度和運動速度有關。約束應力區的概念由Sih等[15]提出，隨后基于約束應力區建立了多種多尺度裂紋模型[15-19]，還建立了宏微觀跨尺度疲勞裂紋擴展統一模型[20]。本文主要工作是在運動裂紋尖端引入約束應力區后，裂紋張開位移在Rayleigh波速下實現了連續，且直到剪切波速都是連續的。

1約束應力區概念與分析模型

約束應力區概念如圖1示，圖1(a)為無損傷的單向受拉板。切開一個長度為a的切口，則切口存在約束應力，如圖1(b)所示。圖1(c)所示為一個長度為a的裂紋。若σ0=σ∞，則情況(b)等價于情況(a)，表示材料無損傷。若σ0=0，則情況(b)等價于情況(c)，表示材料完全損傷。若0<σ0<σ∞，表示材料有一定程度損傷而又沒有完全分離，介于情況(a)與(c)之間。所以，可用約束應力區描述材料的損傷狀態。

圖1　約束應力區概念 Fig.1 Concept of restraining stress zone

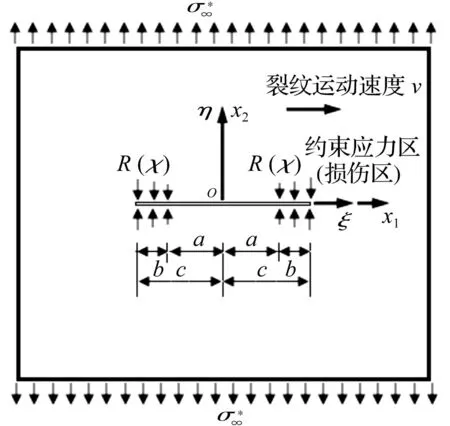
圖2　裂尖具有約束應力區的運動裂紋模型 Fig.2 Moving crack model with a restraining stress zone attached to the crack tip

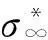
ξ=x1-vt,η=x2

(1)

考慮到裂紋尖端材料有一定程度損傷，裂尖損傷區用一約束應力區來描述，約束應力區內約束應力的分布為R(χ)，χ為局部位置坐標。分布函數R(χ)依賴于裂尖區材料的損傷及裂紋運動速度v，本文考慮線性分布的約束應力，即

R(χ)=f(v)(a1χ+a2),a≤χ≤c

(2)

2基本控制方程

不計休力，二維彈性動力學基本控制方程為Navier方程

(3)

式中:λ與μ為Lame常數，ρ為質量密度，ui為位移。引入體積變形勢函數φ(x1,x2,t)和剪切變形勢函數Ψ(x,y,t)，有

(4)

則式(3)成為

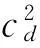
(5)

(6)

采用式(1)的運動坐標系(ξ,η)，式(5)成為

(7)

(8)

引入復變量ζd和ζs

ζd=ξ+iαdη,ζs=ξ+iαsη

(9)

及解析函數F(ζd)與G(ζs)，兩個位移勢函數可表示

φ(ξ,η)=Re[F(ζd)],ψ(ξ,η)=Im[G(ζs)]

(10)

如此，位移與應力解答可表示為[17]

u2(ξ,η)=-Im[αdF′(ζd)+G′(ζs)]

(10)

σ11(ξ,η)=

(11)

σ22(ξ,η)=

(12)

σ12(ξ,η)=

(13)

因此，關鍵是由邊界條件確定出兩個解析函數。

3問題的求解

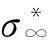
(14)

(15)

(16)

(17)

由式(15)知，D是速度v的函數，當v=cR時，D=0，由此條件可得出Rayleigh波速計算公式為

(18)

圖3運動裂紋表面受兩對對稱集中力作用 Fig.3 Two pairs of concentrated forces symmetrically applied to the moving crack surfaces

下面考慮約束應力單獨作用的結果。如圖3示，對稱位置上dχ上分布力的合力R(χ)dχ可看成是集中力。運動裂紋表面上兩對對稱集中力作用下，解析函數的解答為[7]

(19)

式(2)代入式(19)中，并從a到c積分，即可得出約束應力作用下的解答，有

(20)

(21)

式(20)代入式(21)中，可求出

(22)

遠場應力與約束應力共同作用的結果為

F″(ζd)=F″r(ζd)+F″σ(ζd)

(23)

(24)

(25)

式(16)、(22)代入式(25)中，得

(26)

注意:c=a+b，由式(26)可確定出裂尖損傷區尺寸b。

裂紋表面張開位移COD的定義為

(27)

式(10)、(14)、(20)、(23)、(24)代入式(27)中，求出

(28)

(29)

(30)

4數值結果與討論

假設材料為鋁合金LY12，材料參數見表1。

表1　鋁合金LY12的材料參數

當取g(v)=f(v)=1，a1=0，a2=σ0時，此即運動裂紋Dugdale模型。取σ0=10 MPa,σ∞/σ0=0.4,ξ=0，圖4給出裂紋中點張開位移隨運動速度的變化曲線。由圖4知，vcR時，COD趨于正無窮。v>cR時，COD為負值，且運動速度大于cR情況下逼近cR時，COD趨于負無窮。

為解決以上問題，引入了兩個速度函數g(v)與f(v)，參照文獻[8]，可取

(31)

考慮約束應力為三角形分布，取

(32)

即:χ=a時約束應力為0，χ=c時約束應力為σ0。由式(26)知，此時約束應力區(即損傷區)長度b與速度v無關，僅取決于比值σ∞/σ0，數值結果見表2，裂尖損傷區隨作用荷載的增大而明顯增大。

圖4 裂紋中點張開位移隨運動速度的變化曲線:運動裂紋Dugdale模型Fig.4Normalizedcrackopeningdisplacementatthemiddlepointversusnormalizedcrackmovingspeedcurves:movingcrackDugdalemodel圖5 不同位置裂紋張開位移隨運動速度的變化曲線Fig.5Normalizedcrackopeningdisplacementversusnormalizedcrackmovingspeedcurvesatdifferentlocation圖6 不同應力下裂紋中點張開位移隨運動速度的變化曲線Fig.6Normalizedcrackopeningdisplacementatthemiddlepointversusnormalizedcrackmovingspeedfordifferentstressratio

表2　長度比c/a隨應力比σ ∞/σ 0的變化:σ 0=10 MPa

(33)

(34)

類似地:v=cR時，式(28)中的f(v)/D成為0/0，由羅必塔法則，得

(35)

可見，引入速度函數f(v)后，COD在v=cR時連續且為有限值。圖5也證實，運動速度從0直到剪切波速cs，COD都是連續的，跨越Raylrigh波速時也是連續的。由圖5知，裂紋張開位移隨運動速度增大而減小。

不同作用應力下，裂紋中點張開位移隨運動速度的變化曲線如圖6示，隨荷載的增大，張開位移隨之明顯增大。圖7是不同速度下裂紋張開位移隨橫坐標位置的變化曲線。圖8是不同應力下裂紋張開位移隨橫坐標位置的變化曲線，圖中顯示隨作用應力的增加，裂紋張開位移及裂尖損傷區長度明顯增大。

圖7　不同速度下裂紋張開位移沿橫坐標的變化曲線 Fig.7 Normalized crack opening displacement versus normalized coordinate ξ/a for different crack moving speed

圖8　不同應力下裂紋張開位移沿橫坐標的變化曲線 Fig.8 Normalized crack opening displacement versus normalized coordinate ξ/a for different stress ratio

5結論

(1)研究運動裂紋問題，裂尖損傷區用約束應力區描述。設約束應力為線性分布，采用復變函數解法，獲得了裂尖損傷區長度與裂紋表面張開位移的解析解。

(2)Dugdale運動裂紋模型，在Rayleigh波速下裂紋張開位移為正、負無窮大。通過引入兩個速度效應函數，成功實現了裂紋運動速度從0、到跨越Rayleigh波速、直到剪切波速，裂紋張開位移的連續變化。

(3)數值計算結果表明，隨作用應力的增大，裂尖損傷區長度及裂紋張開位移顯著增大。隨裂紋運動速度的增加，裂紋張開位移明顯減小。

參考文獻

[1]Yoffe E Y. The moving griffith crack [J]. Philosophical Magazine, 1951, 42(7): 739-750.

[2]Hu Ke-qiang, Li Guo-qiang.Constant moving crack in a magnetoelectroelastic material under anti-plane shear loading [J]. International Journal of Solids and Structures, 2005, 42(9-10): 2823-2835.

[3]Hermann K P, Komarov A V, Loboda V V.On a moving interface crack with a contact zone in a piezoelectric bimaterial [J]. International Journal of Solids and Structures, 2005, 42(16-17): 4555-4573.

[4]Lapusta Y, Komarov A, Labesse-Jied F, et al. Limited permeable crack moving along the interface of a piezoelectric bi-material [J]. European Journal of Mechanics-A/Solids, 2011, 30(5): 639-649.

[5]Hu Ke-Qiang, Kang Yi-Lan, Qin Qing-Hua. A moving crack in a rectangular magnetoelectroelastic body [J]. Engineering Fracture Mechanics, 2007, 74(5): 751-770.

[6]Xie C, Liu Y W. Cracking characteristics of a moving screw dislocation near an interfacial crack in two dissimilar orthotropic media [J]. Theoretical and Applied Fracture Mechanics, 2008, 50(3): 214-219.

[7]Sih G C, Jones R.Crack size and speed interaction characteristics at micro-, meso- and macro-scale [J]. Theoretical and Applied Fracture Mechanics, 2003, 39(2): 127-136.

[8]Tang X S, Sih G C. Kinetics of microcrack blunting ahead of macrocrack approaching shear wave speed [J]. Theoretical and Applied Fracture Mechanics, 2004, 42(2): 99-130.

[9]唐雪松. 宏微觀雙尺度運動裂紋模型面內拉伸下的解析解[J]. 振動與沖擊, 2011, 30(3): 100-108.

TANG Xue-song.Analytical solution for macro/micro dual scale moving crack model under the in-plane tension[J]. Journal of Vibration and Shock, 2011, 30(3): 100-108.

[10]王云濤, 呂念春, 程靳, 等. Ⅲ型運動裂紋在兩種邊界條件下的位錯分布函數[J]. 工程力學，2008，25(10): 117-121.

WANG Yun-tao, Lü Nian-chun, CHENG Xin, et al. Dislocation distribution functions of mode Ⅲ moving crack under two boundary conditions[J]. Engineering Mechanics, 2008，25(10): 117-121.

[11]程站起, 華利民, 衛興. 功能梯度材料涂層平面運動裂紋分析[J]. 力學季刊, 2008, 29(1): 78-84.

CHENG Zhan-qi, HUA Li-min, WEI Xing.Moving crack analysis in a functionally graded coating under plane deformation[J]. Chinese Quarterly of Mechanics, 2008, 29(1): 78-84.

[12]胡克強, 仲政, 金波. 功能梯度壓電板條中電絕緣型運動裂紋的電彈性場[J]. 力學季刊, 2003, 24(3): 371-378.

HU Ke-qiang, ZHONG Zheng, JIN Bo. Electroelastic field for an impermeable moving crack in a functionally graded piezoelectric strip[J].Chinese Quarterly of Mechanics, 2003, 24(3): 371-378.

[13]陳增濤, 余壽文. 不同壓電介質界面上的反平面運動裂紋[J]. 固體力學學報, 1999, 20(1): 77-81.

CHEN Zeng-tao, YU Shou-wen.Anti-plane crack moving along the interface dissimilar piezoelectric materials[J]. Chinese Journal of Solid Mechanics, 1999, 20(1): 77-81.

[14]Rosakis A J, Samudrala O, Coker D. Cracksfaster than the shear wave speed [J]. Science, 1999, 284(5418): 1337-1340.

[15]Sih G C, Tang X S. Dual scaling damage model associated with weak singularity for macro-scopic crack possessing a micro-/meso-scopic notch tip [J]. Theoretical and applied fracture mechanics, 2004, 42(1): 1-24.

[16]Tang X S, Sih G C. Weak and strong singularities reflecting multiscale damage: micro-boundary conditions for free-free, fixed-fixed and free-fixed constraints [J]. Theoretical and Applied Fracture Mechanics, 2005, 43(1): 5-62.

[17]Tang X S, Sih G C. Edge dislocations generated from a microcrack under initial residual stress of non-uniform distribution [J]. Theoretical and Applied Fracture Mechanics, 2005, 44(3): 208-233.

[18]Sih G C, Tang X S.Triple scale segmentation of non-equilibrium system simulated by macro-micro-atomic line model with mesoscopic transitions [J]. Theoretical and Applied Fracture Mechanics, 2005, 44(2): 116-145.

[19]Tang X S, Sih G C.Equilibrium mechanics model of multiscaling by segmentation: asymptotic solution for macro-meso-micro damage in anti-plane shear deformation [J]. Theoretical and Applied Fracture Mechanics, 2005, 44(1): 1-15.

[20]唐雪松, 趙小鵬. 疲勞裂紋擴展行為的跨尺度分析方法[J]. 工程力學, 2012, 29(10): 20-26.

TANG Xue-song, ZHAO Xiao-peng.Multiscaling analysis approach of fatigue crack growth behavior [J]. Engineering Mechanics, 2012, 29(10); 20-26.

[21]Freund L B. Dynamic Fracture Mechanics[M]. London: Cambridge University Press, 1990. E Y. The moving griffith crack [J]. Philosophical Magazine, 1951, 42(7): 739-750.