基于Mat lab的少片簧非線性優化及其用戶界面設計

1、陜西西安重裝礦山電器設備有限公司 李弘 2、陜西西安理工大學機械與精密儀器工程學院 柴星

基于Mat lab的少片簧非線性優化及其用戶界面設計

1、陜西西安重裝礦山電器設備有限公司 李弘 2、陜西西安理工大學機械與精密儀器工程學院 柴星

本文結合卡車懸架結構，確定少片變截面鋼板彈簧的截面形狀，再基于Matlab優化工具箱中的Fmincon非線性優化函數對卡車少片變截面鋼板彈簧進行了結構尺寸優化，并要求少片變截面鋼板彈簧的剛度達到預期水平。在此引用某卡車鋼板彈簧的具體數據為例，對其進行優化計算，得出正確優化結果。最終運用M atlab中的GU IDE（Graphics User Interface Design Environment）模塊進行具有良好的人機交互能力的優化軟件界面設計。

少片變截面鋼板彈簧；Fm incon；GUIDE；非線性約束；優化設計

1 引言

少片變截面板簧具有制造方便、結構簡單、節省材料等諸多優點，只要與減振器合理配置，就能極大地改善行駛平順性。本文通過MATLAB軟件優化工具箱中的Fmincon函數，根據少片變截面鋼板彈簧的實際工況、約束條件和剛度要求為對其進行參數優化設計，達到在滿足剛度、強度以及尺寸約束的條件下質量最輕。并通過GUIDE模塊進行用戶界面設計，優化界面采用全漢字化提示和操作界面，使用方便，簡單易學，整個計算過程中不需要任何人為的計算，大大提高計算效率。

2 數學模型的建立

在理論基礎上，將鋼板彈簧（以下簡稱簧片）加工成等應力梁的形狀，使得簧片每一處的最大應力相等是最合適的。如此一來，簧片各截面的厚度沿長度方向應加工成拋物線形狀。但是這種形式的簧片的端部無法承受切向應力，故在工程應用上是不現實的。如果要使得簧片能夠承受切向應力，則需要提高卷耳的強度。根據板簧裝配情況，通常將簧片做成等厚度變截面形狀。這樣盡管能提高板簧的強度，但是整個拋物線形段都處于高應力集中危險區域，這樣的結構布局對材料本身以及加工缺陷都具有很大的敏感性，何況拋物線形鋼板彈簧制造工藝復雜、困難，因此在實際運用中大多使用梯形變厚度截面鋼板彈簧來代替，這兩種簧片的幾何形狀如圖1所示。

圖1 兩種彈簧的幾何形狀

利用虛荷法，可求得載荷作用點處（簧片末端）的變形，繼而可得到簧片剛度，可推得長度為2l的對稱梯形葉片板簧的剛度為：

J2=nbh23/12（n為板簧片數）；

式中，α=l1/l2；

β=h1/h2；

γ=α/β=l1h2/l2h1。變形系數f值可以根據已知的幾何參數α、β由變形系數圖查出。由于實際加工出的板簧截面形狀并不像理論計算那樣為矩形斷面，板簧的實際慣性矩比理論值小，因而使用剛度計算公式計算板簧剛度時需再乘以一個經驗修正系數ζ，一般ζ=0.92。

2.1 設計變量

我們在這里只對鋼板彈簧的一半進行分析，梯形變截面鋼板彈簧的設計變量如下：長度l、端部厚度h1、中部厚度h2、片數n、寬度b。鋼板彈簧看寬度根據不知情況而定，設計懸架時可以選擇適當的值；設計變量根據所需變量定為4個，即

2.2 目標函數

為了保證車輛輕量化的設計理念，并且必須保證鋼板彈簧的使用性能，因此本文將理論上所需要的最小質量設置為目標函數，則得到的目標函數為：

F(X)=2ρbn[x1x3+0.5(x4-x3-l3)(x1+x2)+x2l3]；

式中，ρ為板簧的材料密度，對于Q235鋼，取ρ=7.8×10-6kg/mm3。

2.3 約束條件

根據懸架的總體布置（包括剛度、強度、尺寸規格、制造工藝等）方面的要求，本文將優化問題的約束歸納為以下線性和非線性約束方程。

2.3.1 線性約束

（1）根據鋼板彈簧卷耳處的受力情況分析可知，要使其在卷耳處有足夠的強度，卷耳處的厚度必須大于最小許用厚度，因此得到有線性約束方程：

g1(X)=x1-H1≥0。

（2）根據軋制技術了解到，應將彈簧的最大厚度h2約束在最大淬透厚H2度之內，因此則得到線性約束方程：

g2(X)=H2-x2≥0。

（3）本次設計是梯形變截面鋼板彈簧，故彈簧中部和端部厚度不僅不同，且最少應大于1mm，因此得到線性約束方程：

g3(X)=x2-x1-1≥0。

（4）彈簧末端卷耳尺寸必須大于零，得到線性約束方程：g4(X)=x3≥0。

（5）根據整車布局的實際情況，鋼板彈簧的主片簧必須限制在允許長度L/2之內，得到線性約束方程：

g5(X)=L/2-x4≥0。

2.3.2 非線性約束

(1)為了確保車輛具有良好的行駛平順性，彈簧剛度K與設計要求的剛度值Kc的誤差應小于期望精度值Ke，故得非線性約束方程

而彈簧剛度計算如下，

式中，ζ是修正系數，取0.92；

(2)根據鋼板彈簧的應力分布情況，l1段內的最大應力應小于許用應力[σ]1，因此得到非線性約束方程：

(3)為滿足鋼板彈簧的強度要求，在施加在彈簧上的載荷作用下，彈簧的計算應力應小于材料的許用應力[σ]2，因為最大應力有可能分布在l1段也有可能分布在l2段，因此得到非線性約束方程：

綜上所述，少片簧結構優化設計是一個四維、八個不等式約束的、以質量最小為目標函數并且設定期望剛度值的多目標非線性規劃問題。

以某卡車懸架板簧為例，其具體參數如表1所示：

表1 前鋼板彈簧具體參數

改變彈簧的片數來進行優化。優化結果如表2：

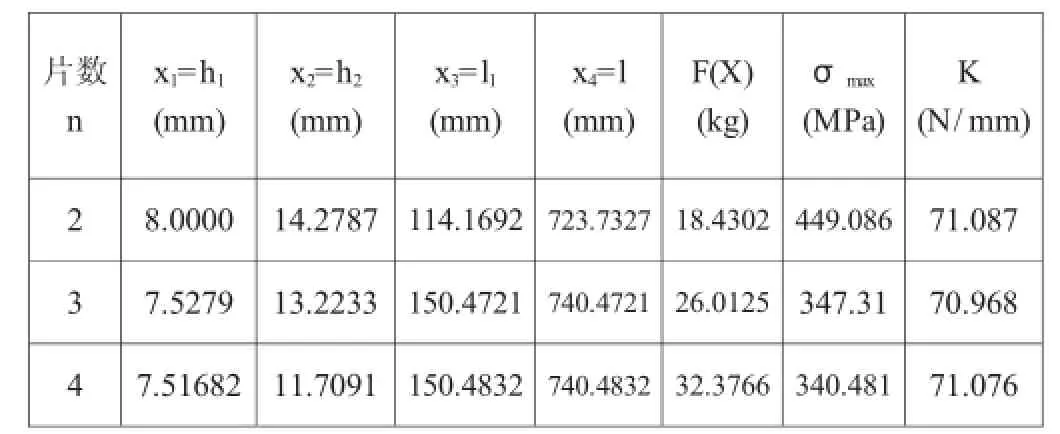
表2 優化設計結果

此例將期望剛度值設置為71N/mm，其經過48次計算的剛度逼近曲線圖如圖2所示。

圖2 剛度逼近曲線圖

至此完成了優化程序的設計，通過GUI進行界面設計后，運行如圖3所示。

圖3 運行狀態下的主界面

3 結論

本文建立了少片變截面鋼板彈簧的數學模型，并對其進行了優化計算。在此利用MATLAB優化工具箱計算出變截面鋼板彈簧的設計參數，不僅保證了強度和剛度以及尺寸要求，而且使鋼板彈簧質量減輕，最輕可達18.43kg，比原鋼板彈簧輕34%且簡單易行、求解精度高、速度快。在此對該程序進行了GUI用戶界面設計，大大減輕了工作人員設計少片變截面鋼板彈簧的設計周期，工作效率得到了極大的提高。

[1]佟剛,任飛.利用MATLAB優化設計少片變截面鋼板彈簧[J].沈陽航空工業學院學報,2000年12月第17卷第4期.

[2]趙云,鄭財權.汽車變截面鋼板彈簧的優化設計[J].設計技術.

[3]鄭銀環,張仲甫.少片變截面鋼板彈簧優化設計[J].機械, 2004年第31卷增刊.

[4]劉惟信主編.汽車設計[M].清華大學出版社,2001.7.

[5]王望予主編,汽車設計（第三版）[M].機械工業出版社, 2000.5.

[6]葉元列主編,機械優化理論與設計[M].中國計量出版社.

[7]蔣立盛,方堅.少片彈簧的設計及其尺寸參數的選擇[J].汽車技術,84.No.6.

[8]彭莫,高軍.變截面鋼板彈簧的設計計算[J].汽車工程,92. No.3.

[9]張寶生.汽車優化設計理論與方法[M].機械工業出版社,2000.

[10]陳江義.面向對象的少片變截面板簧設計[J].汽車研究與開發,1998.(2).

[11]彭莫.變斷面鋼板彈簧的設計計算[J].汽車工程,1992,(3)：156-169.

[12]陳江義.面向對象的少片變截面板簧優化設計[J].汽車研究與開發,1998.(2)：12-15.

[13]于翔.少片變截面鋼板彈簧的設計計算[J].汽車研究與開發,1995,(3)：33-36.

[14]施陽.MATLAB語言工具箱實用指南[M].西安：西北工業大學出版社,1998.100-120.

李弘，1971出生，陜西河陽人，本科，工程師，研究方向：礦用機電機械機構。