一種有效提高儀器精度的建模方法

一種有效提高儀器精度的建模方法

賈云濤，胡耀元，張建永，岳偉

(北京無線電計量測試研究所，北京 100039)

摘要：提出了一種能夠有效提高儀器儀表測量精度的建模方法。該模型結合改進的灰色系統和粒子群優化算法，通過測試數據對模型訓練后得到儀表滿量程內誤差的擬合模型，進而可對儀器量程內任意測量值進行修正。通過實驗證明，該模型具有經濟性、實用性和準確性高的特點。

關鍵詞：灰色系統；離子群優化算法；儀表精度

doi：10.11823/j.issn.1674-5795.2015.04.04

中圖分類號：TB97；O24

收稿日期：2015-01-24

作者簡介：賈云濤(1986-)，男，工程師，碩士，主要從事電學計量科研和測試工作。

An Effective Modeling Approach to Improve Meter Accuracy

JIA Yuntao，HU Yaoyuan，ZHANG Jianyong，YUE Wei

(Beijing Institute of Radio Metrology & Measurement，Beijing 100039，China)

Abstract：This paper presents a modeling approach which can effectively improve meter accuracy.This model，which combines the improved gray system and particle swarm optimization，uses a small amount of the instrument known error data as training data to get the full-scale error fitting model.Then the model can be used to amend all values in the range.The system has the advantages of economy，practicality and high accuracy proved by experiments.

Key words：gray system；particle swarm optimization；meter accuracy

0引言

儀器儀表品種繁多，已被廣泛應用于工業、醫療和科研等領域中。伴隨著科學技術的進步，儀器儀表越來越復雜化、集成化和高科技化。而隨著使用時間的累積，儀器儀表也表現出精度下降、可維修性差的問題。由于影響儀表精度的因素具有多樣性，有已知的也有未知的，這就為提高儀器的精度帶來了很大的困難。

本文提出了一種粒子群非齊次灰色模型對儀表測量數據建模的方法。該模型改變了傳統依靠硬件優化提高儀表精度的思想，具有通用性、經濟性和有效性。

1三種建模方法

1.1灰色模型

灰色系統理論是一種用來解決信息不完備系統的數學方法，尤其適用于影響因素多樣并且未知的系統[1-2]。影響儀器儀表精度的原因多種多樣，有儀表電壓、元器件老化、環境干擾等因素，這些因素又無法用數學量化，因此可以將儀表的誤差影響系統看作是一個灰色系統進行研究[3]。

其建模方法可描述為：

設訓練序列X(0)為非負序列：

X(0)={x(0)(1)，x(0)(2)，x(0)(3)，...，x(0)(n)}

式中：x(0)(k)≥0，k=1，2，…，n。

將模型訓練序列進行一次累加生成，得到序列為X(1)：

X(1)={x(1)(1)，x(1)(2)，x(1)(3)，...，x(1)(n)}

(1)

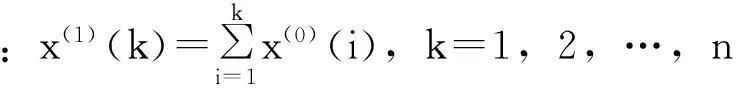
Z(1)為X(1)的緊鄰均值生成序列：

Z(1)={z(1)(1)，z(1)(2)，…，z(1)(n)}

(2)

式中：z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)，k=1，2，…，n。

稱x(0)(k)+az(1)(k)=b為GM(1，1)模型。

若Z=(a，b)Τ為參數列，且

(3)

則可通過最小二乘估計求解微分方程x(0)(k)+az(1)(k)=b中的系數。

(4)

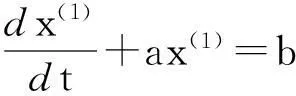
通過數學求解可得到白化方程的時間響應函數為

(5)

得到的式(5)即代表序列一次累加和的時間響應曲線，再進行反運算即得到訓練序列的相應函數曲線，代表著訓練序列的趨勢軌跡。

1.2粒子群算法

粒子群算法即PSO算法(Particle Swarm Optimization)，是基于群體智能的一種尋找最優解的優化算法[4]。

應用PSO算法求解最優解有兩個很重要的步驟：編碼和適應度函數。PSO算法對粒子直接編碼，粒子在進化過程中通過適應度函數的反饋確定最優粒子，然后通過式(6)和(7)更新粒子的速度和位置，不斷逼近最優解，當達到終止條件時，停止進化。

vij(t+1)=wvij(t)+c1×rand()×(pbestij-xij(t))

+c2×rand()×(gbestj-xij(t))

(6)

xij(t+1)=xij(t)+vij(t+1)

(7)

式中：w是代表運動慣性的參數，較大的w有利于群體在更大的范圍內搜索，較小的w能夠保證群體收斂到最優位置，一般設置為0.8左右；c1和c2用于調整種群自身經驗和社會經驗在其運動中的作用，表示個體向pbest(自身最優位置)和gbest(群體最優位置)加速項的權重；rand()是介于(0，1)之間的隨機數，在初始化階段用來定義粒子的初始位置和初始速度。

1.3PSO-NGM模型

在灰色模型的基礎上加入非齊次方程量，并結合粒子群優化算法求解得到組合模型，即粒子群非齊次灰色模型PSO-NGM(Particle Swarm Optimization Non-homogenous Grey Model)。將它應用于提高儀器精度上的思想就是：選取標準儀器對待測儀器量程內進行少量數據測試，將標準與被測儀器示值差作為誤差，用誤差數據去訓練PSO-NGM模型就可以得到儀器滿量程內誤差模型。進而可對被測儀器滿量程內任意測量值進行修正，提高儀器精度。

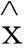
(8)

式中：v，C1，C2，C3，C4為待定系數。

由公式(8)可以看出，新改進的方程不僅具有原來指數的模型，還增加了直線和拋物線的擬合模型[7-8]。因此比原灰色系統更具有適用性。

2求解PSO-NGM模型

PSO-NGM模型訓練的流程圖如圖1所示。

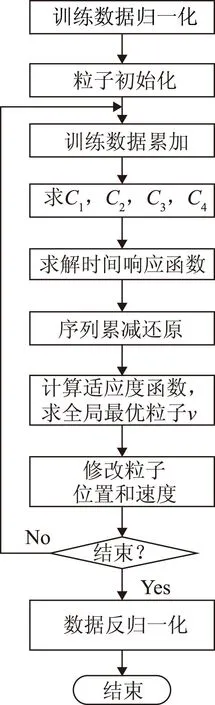
圖1　PSO-NGM模型訓練流程圖

2.1歸一化和反歸一化

由于模型應用了灰色系統理論，而灰色理論中要求訓練數據為非負。現實中儀器測量誤差不可能保證總為正數，因此，需要先對原始誤差數據進行歸一化處理，有

(9)

式中：xmin和xmax代表數據中的最小和最大值；(0)代表歸一化的最小值是0值。

得到的新數據是一系列在(0，1)范圍內的歸一化數據，可以用來進行模型訓練。同理，在模型訓練結束再進行反歸一化得到復原的數據值。

2.2初始化過程

用離子群優化算法尋求最優解需要先對代表解的粒子進行初始化，包括粒子初始速度和位置、迭代次數和種群大小等。

2.3參數v，C1，C2，C3，C4的求解過程

通過粒子群算法不斷迭代優化得到最優粒子v的值后，令

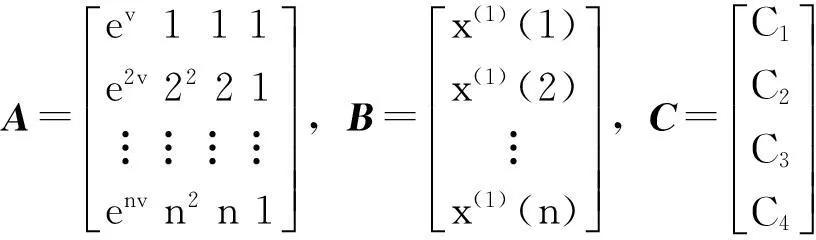
(10)

應用最小二乘法可求得參數C1，C2，C3，C4的估計值：

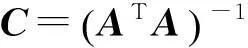
(11)

2.4數據還原過程

根據PSO算法和最小二乘法迭代后可得到v，C1，C2，C3，C4的值，即得到了序列累加后的擬合方程式(8)，再經過累減運算就可以得到還原序列：

(12)

2.5粒子速度和位置更新過程

每次優化后根據每個粒子對應的適應度函數大小判定粒子的優劣。求取全部粒子中的最優粒子。其他粒子根據式(6)和式(7)改變位置和速度后繼續進化，直到達到指定的進化次數為止。

3PSO-NGM模型的應用分析

3.1模型訓練

為了驗證所建模型的正確性和有效性，我們特選取在工業生產和各大行業都普遍用到的數顯表頭作為研究對象。選取某型號數顯表，在0～50 V量程內抽點進行電壓值測量，然后應用本文模型對其誤差進行訓練[9]。實驗中，我們選用了一組較均勻的分布于數顯表量程內的電壓測量點，測量時，選用標準器5720A的輸出電壓作為標準電壓，數顯表顯示的電壓作為測量電壓。其顯示值與標準值之差作為誤差進行模型訓練。為了證明本文模型的有效性，將修正后的結果與基本灰色模型系統修正的結果進行對比。

在0～50 V量程內包括最低、最高值點的等間距選取6個測試點。得到該數顯表顯示值與標準值誤差如表1所示。

根據公式(9)，將絕對誤差歸一化到(0，1)范圍，結果見表1。

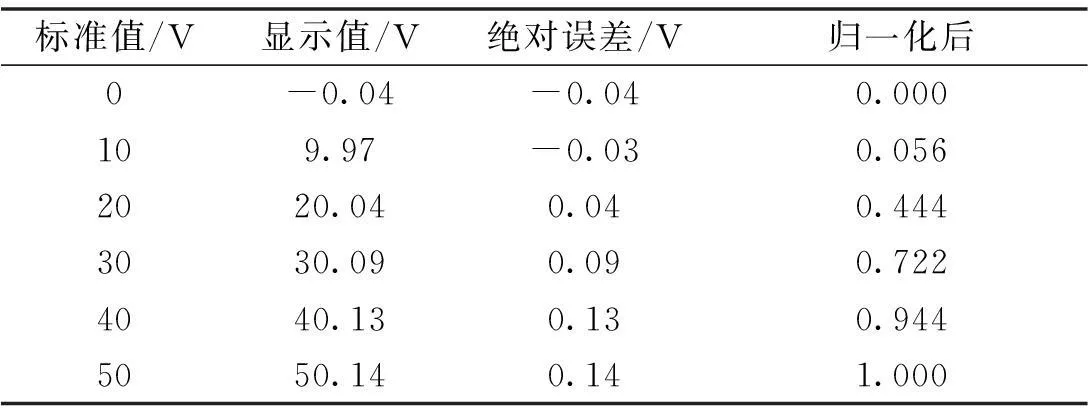
表1　顯示值與標準值誤差及歸一化結果

PSO算法在本模型中只優化一個未知解，可初始化粒子群的維數為1，初始數目為200，根據v的預估值，設置粒子初始位置和初始速度分別為(0，1)和(-0.1，0.1)內的隨機數。設置終止條件為疊代次數達到500。應用已有的6個歷史誤差數據，選取所有訓練數據擬合值與實際值的最小誤差和作為適應度函數，尋求最優粒子解[10]。

3.2結果分析

使用PSO-NGM模型最終得到訓練數據和擬合數據的對比如表2所示。圖2顯示了應用本文模型與GM模型擬合效果的對比。圖3和圖4分別為粒子群優化過程中適應度值的變化過程和最優粒子解的優化過程。

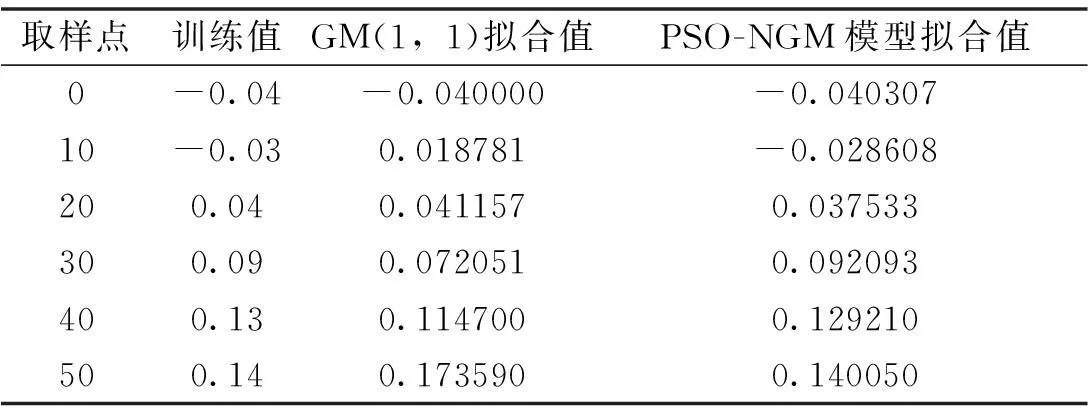
表2　PSO-NGM模型對訓練數據的

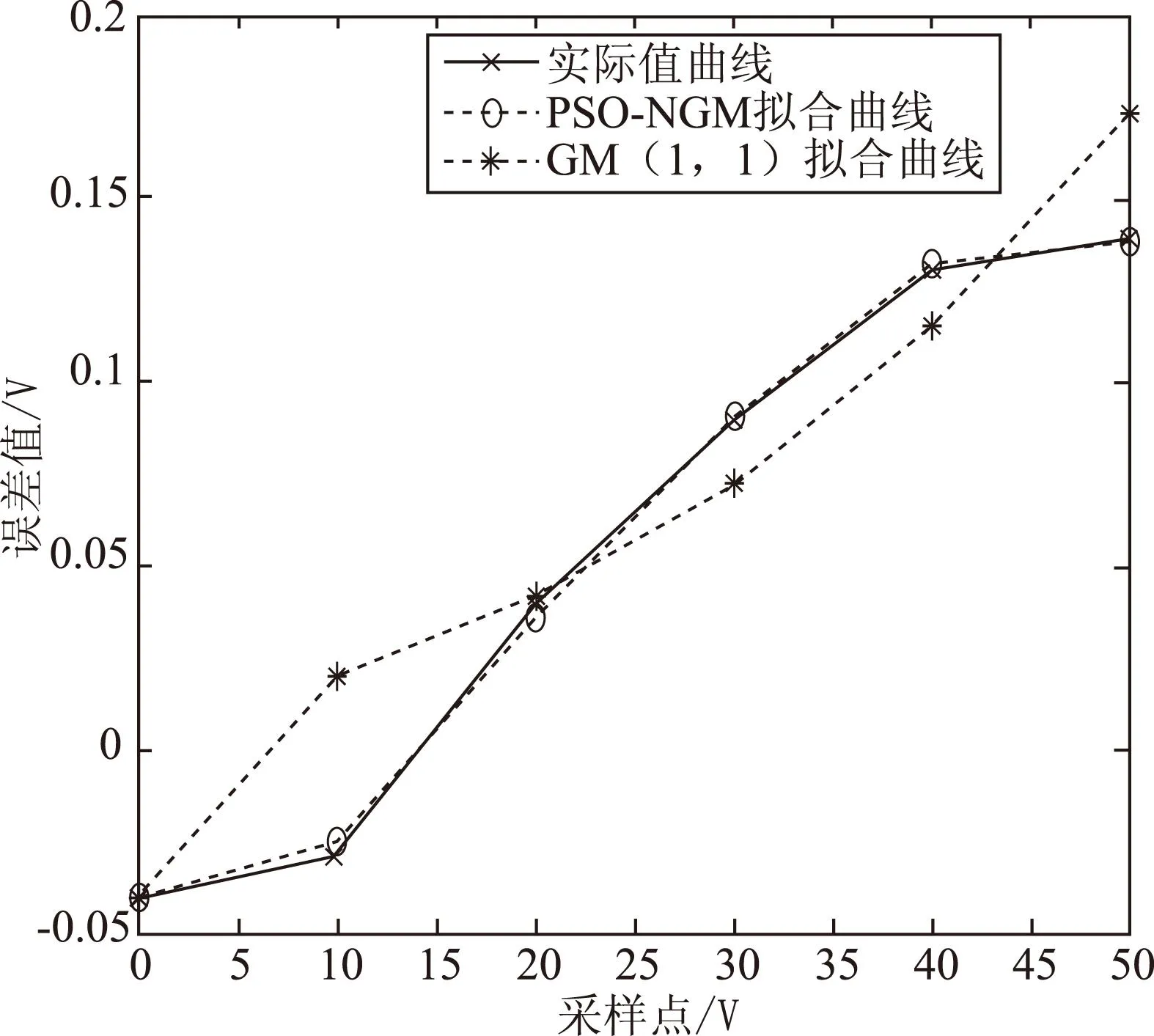
圖2　PSO-NGM模型與GM(1，1)模型訓練結果對比圖

圖3　PSO-NGM模型中適應度值的變化

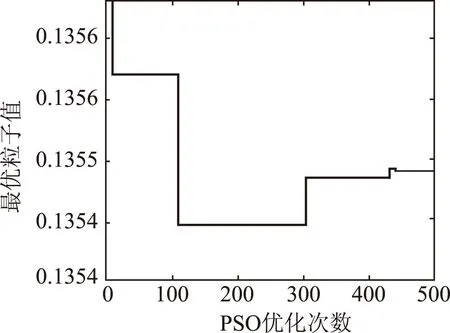
圖4　PSO-NGM模型中最優粒子的變化

從圖2可以看出本文提出的PSO-NGM模型比灰色模型能更好地擬合儀器誤差的曲線。

3.3模型驗證

應用標準源5720A對數顯表量程內一組電壓點隨機測量，分別應用GM(1，1)模型和PSO-NGM模型對誤差進行修正。將修正結果與標準值進行比較，對比情況如表3所示。

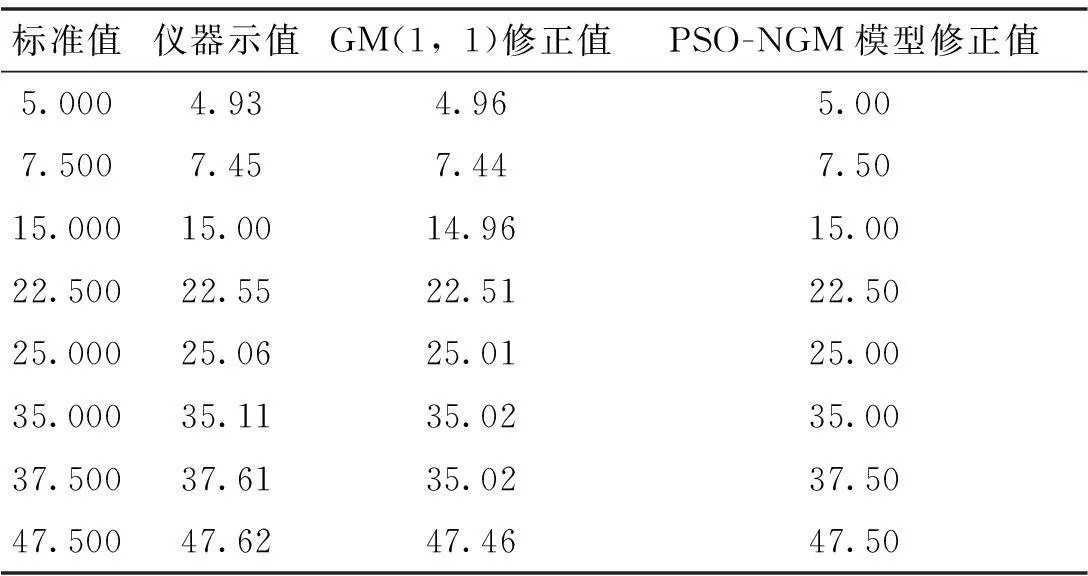
表3　PSO-NGM與GM(1，1)模型

由表3可以看出，灰色模型雖然能夠對儀表誤差進行少量修正，但也出現了錯誤修正，而本文提出的PSO-NGM模型卻能夠對測量結果進行準確的修正，證明該改進模型克服了原始灰色模型適用性差的缺點，能夠適用于儀表誤差的修正。

4總結

本文提出了一種結合灰色系統和粒子群優化算法的數學模型。該模型具有訓練數據少，適用性強和精度高的優點，可應用于對儀器示值誤差進行修正而不需改變儀器的硬件，具有廣闊的應用前景和實用價值。

參考文獻

[1] Yang G，Wu X.Fault prediction of ship machinery based on gray neural network model[C]//Proc.of the 6th IEEE International Conference on Control and Automation.Guangzhou，China：IEEE，2007：1063-1066.

[2] 彭宇，劉大同，彭喜元.故障預測與健康管理技術綜述[J].電子測量與儀器學報，2010，24(1)：1-9.

[3] Cheng S，Pecht M.A fusion prognostics method for remaining useful life prediction of electronic products[C]//IEEE，2009：102-107.

[4] 唐陽山，方媛，白艷，等.基于蟻群算法的交通出行生成預測方法的研究及應用[J].遼寧工業大學學報：自然科學版，2009，(02)：108-110.

[5] 何斌，蒙清.灰色預測模型拓廣方法研究[J].系統工程理論與實踐，2002，9(9)：137-140.

[6] 仇芝.灰色組合模型研究與應用[D].南京：南京航空航天大學，2006.

[7] 陳鵬宇，段新勝，項翔.優化白化方程參數的新NGM(1，1，k)模型及其應用[C]//第19屆灰色系統全國學術會議.北京：中國高等科學技術中心，2010：299-304.

[8]柯鏵，柯科，灰色模型的擴展及應用[J].蘭州理工大學學報，2013，39(6)：152-155.

[9] 潘亞林，鄭樹湘.應用灰色系統模型提高儀器精度[J].低溫與超導，2002，30(1)：64-67.

[10] 賈云濤.基于改進灰色系統的電力電子裝置故障預測技術研究[D].南京：南京航空航天大學，2012.