一種基于SIFT特征的快速圖像匹配算法

摘要：針對SIFT算法運行速度較慢、時間效率不高的問題，本文提出了一種與Harris角點檢測算法相結合的快速圖像匹配算法。該方法利用Harris角點檢測算法計算量小，運行速度快的優點，并改進SIFT算法描述子，通過調整描述子的結構達到特征向量降維的目的，進一步提高算法的時間效率。實驗結果證明，該算法既保留了SIFT算法的穩定性以及旋轉不變性，也提高了SIFT算法的運行速度。

關鍵詞：圖像匹配；SIFT特征；Harris角點檢測

中圖分類號：TP391.41

文獻標識碼：A

DOI：10.3969/j.issn.1003-6970.2015.06.011

本文著錄格式：任忠良，一種基于SIFT特征的快速圖像匹配算法[J].軟件，2015，36（6）：53-57

AFastImageMatchingAlgorithmBasedonSIFTFeatures

RENZhong-liang[Abstract]：AnewalgorithmisproposedcombinedwithHarriscornerdetectionalgorithm，inordertoimprovetheefficiencyofSIFTwhichrunsslowlyandhaslowefficiencyonfeaturesextracting.ItmakesfulluseofHarris'lowcalculationfastoperation.BychangingtheSIFTdescriptor，itachievesthegoalofdecreasingtheeigenvectorthroughimprovingthestructureofthedescriptor.Astheexperimentalresultsshow，thisalgorithm，notonlyretainsthestabilityandrotationinvarianceofSIFT，butalsoimprovesthespeedofSIFTalgorithm.

[Keywords]：Imagematching；SIFTfeatures，Harriscornerdetection

0引言

隨著人T智能的不斷發展，圖像匹配技術逐漸成為模式識別領域中一項非常重要的技術，其在諸多領域有著廣泛的應用，如遙感衛星地圖和地形匹配、醫學診斷、人臉識別等等。基于圖像局部特征的匹配算法是圖像匹配技術中較為常見的算法，該類算法的思想是將圖像映射為包含該圖像局部特征信息的集合，以此來進行圖像匹配。其中，SIFT（Scale-invariantfeaturetransform，尺度不變特征轉換）算法是一種較為經典的利用圖像局部特征的匹配算法。SIFT算法[1-2]由Lowe于1999年提出，它基于尺度空間理論，具有穩定性好、特征點準確性強等優點，對旋轉、尺度、光照等保持較好的不變性。

但SIFT算法也有其一些弊端，其中建立尺度空間需要較大的系統開銷，時間效率較低。國內外基于SIFT算法的改進也有大量的研究。如KeandSukthankar[3]提出的PCA-SIFT算法，利用PCA（Principlecomponentanalysis，主要成分分析）將特征點描述向量降至36維；MikolajczykandSchmid[4]提II+Il-種SIFT變體描述子-GLOH（TheGradientLocation-OrientationHistogram，梯度定位方向直方圖），利用對數極坐標代替Lowe使用的坐標象限；HerbertBay等人[5]提出的SURF（Speed-upRobustFeatures，快速魯棒特征）算法選用二階標準高斯函數作為濾波器，通過改變濾波器大小來建立尺度空間，可以有效提高算法的效率；張春美等人[6]對SIFT描述子進行改進，利用同心網環描述特征點，保持旋轉不變性的前提下降低了描述子的維度；陳抒珞等人[7]提出Contourlet-SIFT變換，對特征及其鄰域先進行Contourlet變換，構建全局紋理描述向量，以提升匹配速度；范志強等人[8]將SIFT與數據聚類做結合，提高了特征匹配的魯棒性。本文主要針對SIFT算法提取特征點時效性差這一缺點進行改進，結合Harris角點[9]提取算法，能夠有效的提高關鍵點的提取速度，并適當降低描述子維度，以此來降低算法運行所需的時間，增強算法的實時性。

1SIFT算法原理

SIFT算法基于Lindeberg等人[10]提出的尺度空間理論，利用高斯核建立尺度金字塔，在尺度空間尋找極值點，并賦予該點對尺度、旋轉保持不變性的特征向量，并利用這些特征向量間的歐氏距離來進行匹配，以達到圖像匹配的目的。

1.1查找關鍵點

文獻[10]證明了高斯卷積核是生成尺度空間的唯一變換核。一幅圖像/（x，y）的尺度空間定義為L（x，y，б），是由不同尺度的高斯函數與原圖像卷積運算生成的[10]。

L（x，y，б）=G（x，y，б，）*（x，y）

（1）

其中，

高斯核的尺度б是連續變化的，將其與原圖像進行卷積運算，得到一組尺度空間圖像。將得到的圖像進行降采樣作為相鄰組高斯圖像的基準圖像，繼續與高斯核進行卷積運算得到新一組尺度空間圖像。如此反復直至圖像大小小于某個預定值。將相鄰層的高斯圖像進行相減便得到DOG（DifferenceofGaussian）圖像D（x，y，б）。

Lowe在DOG尺度空間中尋找極值點，將其中每個點與相鄰尺度的對應位置包括其相鄰位置以及本尺度的八個相鄰位置共計26個點逐個進行比較，得到的局部極值位置和尺度即為極值點的位置和對應的尺度。極值點即為后文敘述中的關鍵點。

1.2分配方向

SIFT算法中為每個關鍵點分配主方向時采用關鍵點鄰域的梯度分布，并且在1.3章節中描述符構造也以此方向作為參照。

各像素梯度的模與方向的計算公式如下：

1.3生成描述符

生成描述符時，為保證其旋轉不變性，首先將關鍵點周圍區域旋轉順時針旋轉θo，與主方向相同。在旋轉后的區域內，對關鍵點周圍16x16矩形窗口采樣。Lowe建議將其分成16個4x4的子區域，并在每個子區域中將方向投影至8個方向的梯度累加值，則共生成4x4x8共計128維向量，該向量即為SIFT算法的128維描述符，如圖1（以其中8x8為例）所示。

至此，SIFT特征描述符已具有尺度、旋轉不變性，將描述符進一步做歸一化處理后可去除光照影響。并且SIFT算法中的鄰域方向也提供了較好的穩定性，使得SIFT算法具有較高的魯棒性。

1.4特征向量的匹配

Lowe在原文中建議利用兩幅圖像檢測到的特征向量之間的歐式距離之間的比值作為匹配依據，具體步驟如下：在其中一幅圖像取關鍵點，并在另一幅圖像中根據歐式距離選取最近的前兩個關鍵點，若最近的距離除以次近的距離少于某個比例閾值，則接受這一對匹配點。歐氏距離定義及判定閾值公式如下：

根據公式（7）不難看出，將比例閾值Threshold增大，SIFT算法的匹配點對會增多。反之，降低比例閾值Threshold，匹配點對會減少，但匹配更加穩定。文獻[2]中建議該閾值取值為0.8，本文算法根據經驗值將該閾值設為0.75。

2改進的快速SIFT圖像匹配算法

由于在1.1章節中介紹的尺度空間中查找極值點的系統開銷較大，導致算法效率較低，其目的是為了能夠找到較多、較為穩定的極值點，并且保證其尺度不變性。但是在實際應用中，若圖像獲取設備能夠保證較好的對焦情況，則進行匹配的圖像尺度就不需進行過多考慮，因此我們考慮與較為快速的犄征點提取算法做結合，以提高SIFT算法的效率。

2.1Harris角點提取算法

Harris算法是以Moravec算法[11]為基礎的，而其原理是將以目標像素點（x，∥）為中心的窗口向任何方向移動（μ，v）后計算灰度變化，Harris在此基礎上，利用微分運算和白相關矩陣來檢測角點，能夠有效區分角點與邊緣。Harris算法具有計算簡單的特點，所以運行速度較快，并且算法具有較高的穩定性和魯棒性，能夠在圖像旋轉、灰度變化以及噪聲干擾等情況下準確的檢測特征點，具有較高的點重復度和較低的誤檢率。

2.2改進的SIFT描述符

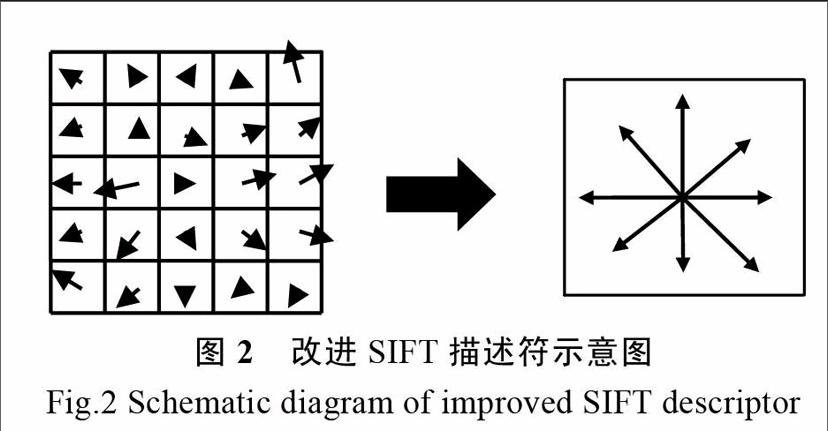
在經過Harris角點提取算法提取特征點，計算并分配方向，以及對齊主方向之后，在關鍵點周圍15x15的區域上采樣計算方向，其中將每個Sx5的區域方向投影到八個方向上，這樣生成的描述子有3x3x8共計72維向量，代替原文的128維向量，以達到降維的目的，如圖2（以其中一個5x5的區域為例）所示。

通過對新的描述符的分析我們可以發現，改進后的描述符在盡可能多的保留采樣區域（16x16改為15x15）的前提下，通過改進描述符的結構來對描述符降維。這樣做既有利于保持SIFT算法的魯棒性，又能夠進一步提高后續匹配的速度。

2.3改進的SIFT算法過程

根據2.2章節的分析，我們現對SIFT算法做如下改進：首先利用Harris角點提取算法對圖像進行關鍵點查找，接著對得到的關鍵點進行主方向分配，并生成72維的改進SIFT描述符，最后利用歐氏距離對兩幅圖像進行匹配，得到匹配結果。算法過程如圖3所示：

3實驗結果與分析

采用MATLABR2013a構建實驗平臺，將本文算法與SIFT算法在匹配效果與時效性方面進行了比較與分析。算法運行環境為CPU：InteI（R）Xeon（R）E3-1230v33.3GHz，內存：8GB。

3.1具有一般場景的圖像匹配

圖4為使用SIFT算法進行匹配的效果圖，而圖5為使用本文算法的匹配效果圖。經分析，不難發現本文方法在特征點的提取方面更接近于視覺角點，特征點的數量雖然較少，但匹配正確率較高，效果較好。使用SIFT算法與本文算法進行圖片匹配的運行時間如表1所示。

由表1可以看出，本文算法在運行時間上相對于SIFT算法有著較為明顯的提升，算法的時間效率較高，尤其是提取極值點的步驟，由于利用了速度較快的Harris算法，使得該步驟所需時間大大降低。并且由于描述子維度降低，使得匹配時間也得以縮短，同時保持較高的正確率。說明本文算法具有較強的魯棒性。

3.2具有較大旋轉角度的圖像匹配

圖6中，圖（a）是經典的Lena圖像，大小為512×512，圖（b）是對其進行30。旋轉后得到的。由于本文主要是針對SIFT算法的速度進行改進，所以將速度較快的經典SURF算法拿來作為參照，似驗證本文所提出算法的時效性，算法運行環境同上。圖6是原SIFT算法的匹配效果圖，從圖中可以看出原SIFT算法匹配效果較好，信息較為豐富，且正確率較高。圖7是SURF算法的匹配效果圖，從圖中可以看出SURF算法匹配雖然信息較為豐富，但就旋轉圖像而言，誤匹配率較高，匹配效果較差。圖8是本文算法的匹配效果圖，從圖中可以看出本文算法匹配效果較好，正確率較高。使用SIFT算法，SURF算法與本文算法進行圖片匹配的運行時間如表2所示。

由表2可以看出，SIFT算法具有旋轉不變性，對于旋轉圖片仍有較高的正確率。而SURF算法雖然時效性強，但針對旋轉圖像則不能保證較高的正確率。而本文算法在保證較高正確率的前提下，依然有著較快的速度表現，表明本文算法具有時效性和旋轉不變性。

4結論

本文針對SIFT算法時間效率較差這一缺陷進行改進，在極值點的提取部分針對較小尺度變換的圖片，采用速度較快，算法較為簡單的Harris算法來代替原有的尺度空間的極值點提取。并在描述符生成時采用新的描述符結構來達到降維的目的，從而進一步提高算法運行效率。從最終的實驗結果圖以及與幾種算法對比的時間結果來看，本文算法既能保證穩定性與正確性，又能降低算法的時間開銷。在接下來的工作中，可以嘗試與一些其他模式識別與匹配算法[12-14]進行結合，以設計出更加有效的算法。

參考文獻

[1]LoweDG.Objectrecognitionfromlocalscale-invariantfeatures[C]//Procofthe7thIEEEIntConfonComputerVision.Piscataway，NJ：IEEE，1999：1150-1157.

[2]LoweDG.Distinctiveimagefeaturesfromscale-invariantkeypoints[J].InternationalJournalofComputerVision，2004，60（2）：91-110。

[3]KeY，SukthankarR.PCA-SIFT：Amoredistinctiverepresentationforlocalimagedescriptors[C]//Procofthe2004IEEEComputerSocietyConfonComputerVisionandPatternRecognition.Piscataway，NJ：IEEE，2004：511-517.

[4]MikolajczykK，SchmidC.Aperformanceevaluationoflocaldescriptors[J].IEEETransonPatternAnalysisandMachineIntelligence，2005，27（10）：1615-1630.

[5]BayH，EssA，TuytelaarsT，etal.Speeded-uprobustfeatures（SURF）[J].ComputerVisionandImageUnderstanding，2008，110（3）：346-359。

[6]張春美，龔志輝，孫雷.改進SIFT特征在圖像匹配中的應用[J].計算機工程與應用.2008.44（2）：95-97.

[7]陳抒珞，李勃，董蓉，等.Contourlet-SIFT特征匹配算法m.電子與信息學報，2013，35（5、：1215-1221.

[8]范志強，趙沁平.一種基于數據聚類的魯棒SIFT特征匹配方法[J].計算機研究與發展，2012，49（5）：1123-1129.

[9]SchmidC，MohrR.Localgrayvalueinvariantsforimageretrieval[J].IEEETransactionsonPatternAnalysisandMachineIntelligence，1997，19（5）：530-534.

[10]LindebergT.Featuredetectionwithautomaticscaleselection[J].InternationalJournalofComputerVision，1998，30（2）：79-116.

[11]MoravecHP.Towardsautomaticvisualobstacleavoidance[C]//ProceedingsofInternationalJointConferenceonArtificialIntelligence.Cambridge.MA.USA：fs.n.].1977：584-590.

[12]郝春媚、楊榆.面向涉密檢查系統的基于KMP思想的多模式匹配算法[J].軟件.2013.34（9）：57-60.[J].[13]楊沐，王晨升，陳志強，等.復雜背景下的字符模板匹配改進算法研究[J].軟件，2012.33（12）：97-100.[J].[14]陳小星，陶志強.一種基于車輛圖像的Keren配準方法的改進算法[J].軟件，2014，35（12）：20-25.