應急物資儲備點選址問題研究

郭繼坤 穆祥靜，2

(1.后勤工程學院，重慶401311;2.海軍工程大學 勤務學院，天津300450)

1 引言

應急物資儲備點選址是應急物資儲備布局優化需解決的關鍵問題，即在現有物資儲備點地址的基礎上，根據可能擔負的任務、地形交通狀況、儲存條件和資源配置等因素，科學確定或調整物資的儲備布局，為國家物資儲備建設和處理突發事件提供更加有效的物資供應。

關于應急物資儲備點選址問題研究，軍內專家多次展開相關研究:如張來順采用運籌學中動態規劃的方法建立數學規劃模型，并采用模型分解與啟發式算法相結合的方法求解［1］;陳陽提出將物聯網技術應用到應急物資儲備布局的觀點［2］;陳智提出在考慮運輸方式和道路換乘的條件下，對實際運距進行標準運距的換算，以達到不同運送方式下保障時效的可比性，選出布局優化方案［3］;雙海軍引入計算機SLAM 仿真技術和綜合評判方法對儲備布局進行優化研究［4］;徐東提出建立構建軍事物資儲備布局評價、調整模型的思路，使得物資儲備布局可隨軍事戰略方針和兵力部署的變化而及時、合理地調整［5］。從以往研究結果看，應急物資儲備點選址問題是一種典型的多目標優化問題，不同學者因目標設定不同和采用方法各異而得出不同的研究結論。

本文采用多目標決策方法對應急物資儲備點選址問題展開研究，與以往研究方法相比較，該方法的創新之處在于:綜合考慮多種影響因素，使優化結果更符合選址實際需求，并且為規避各目標之間存在的矛盾，首先結合軍用標準地圖提供的道路信息，確定各目標的影響因素;其次運用模糊層次分析法，對最“底層”影響要素結合專家打分或經驗取值構造優先關系矩陣，從而確定上級目標的權重系數;最后再對選址問題進行目標決策，使得結果最優。

2 確定應急物資儲備點選址目標

2.1 距離最短

儲備點至最遠需求點的距離在滿足物資保障要求的前提下，越短越優。如:應急物資儲備點距前方為150—200 公里，在此范圍內前送距離越短越好，優化目標是找出距需求點距離最短的儲備點。

2.2 時間最短

儲備點到最遠需求點的時間在滿足最短時間要求的前提下，時間越短越好。如果存在多點儲備，同時多點保障的情況，優化目標是找出到需求點時間最少的儲備點。

2.3 調運成本最少

儲備點到各需求點的總調運成本最少，即物資輸送的總噸公里數最小。這一目標主要針對平時物資供應管理，達到節約目的。

2.4 儲備點建設成本最低

應急物資儲備點建設成本主要指建設的地理費用，包括建筑物、設備、土地和運輸距離等相關費用。此項費用與儲備點的地理位置和規模有關。

2.5 儲備數量在滿足持續消耗需求的前提下最低

儲備點應急物資儲備數量滿足規定時限內的持續消耗要求，多則浪費，少則不能達到保障要求。

3 確立備選應急物資儲備點

應急物資儲備點選址的實施，重點是確立備選應急物資儲備點。備選應急物資儲備點的確立需要考慮儲備點的儲存條件、交通狀況、安全情況和補充的難易度等因素，并不是所有能建立物資庫站的位置都能成為儲備備選點。

3.1 根據任務確定儲備備選點

根據不同任務以及物資來源的情況，選擇儲備備選點。備選點的選取對最優方案和計算求解的過程以及運算成本有著直接的影響。備選點過多，會使模型復雜化，計算工作量劇增;而備選點太少，則可能使所得優化方案偏離最優解太遠，達不到合理布局的目的。

3.2 對各備選點進行綜合評價

確定了應急物資儲備備選點，就要對每個備選點進行具體分析和綜合評價，從整體保障效益的角度出發，權衡該備選點在布局中作用的大小。評價的指標有:①儲存條件，包括水源、地幅、地勢、坡度等;②交通條件，包括附近鐵路、公路狀況，通行程度等;③地形隱蔽條件，包括疏散地域、地表覆蓋情況等;④靠近物資需求點，包括標準運距、實際距離、到達時間;⑤靠近物資供應點，包括實際距離，運送時間。

設有A1，A2，…，Am是評價方案的m個替代方案，x1，x2，…，xn是評價替代方案的n個評價指標，w1，w2，…，wn是n個評價指標的權重，vi1，vi2，…，vin是第i個替代方案Ai的關于xj指標(j =1，2，…，n)的價值評定量，相應的關聯矩陣見表1。

表1 備選點綜合評價關聯矩陣

評價:

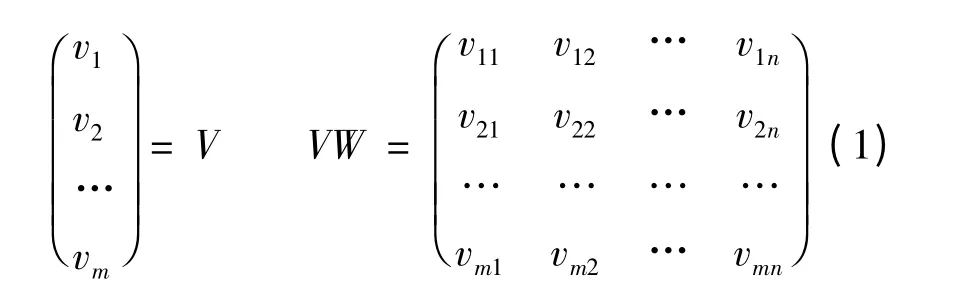
對于不同的評價指標，難以在同一標準下進行比較:交通方便的道路樞紐往往隱蔽條件較差，靠近前方的儲備地點往往安全防護性差，便于物資供應點補充的地域往往又距離前送補充要點太遠。在這種情況下，可用逐對比較法來對不同的評價指標加以權重，即利用所有評價指標對替代方案按照一定的基準進行評分，再利用加權的方法對替代方案的各種評價指標的評價值進行綜合評價。

對評價指標進行兩兩比較，認為相對重要的指標得分定為1，相對不重要的得分定為0，進行比較后的評價指標權值見表2。

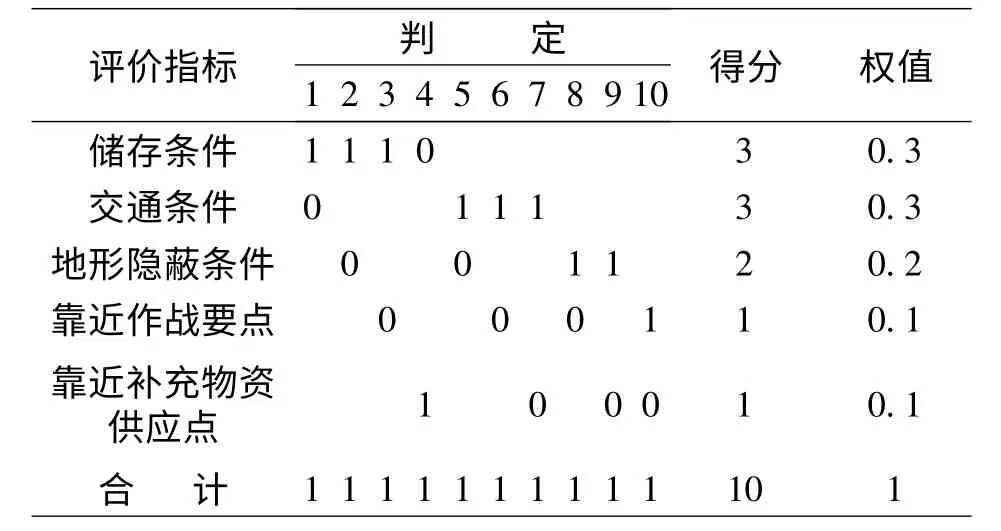
表2 用逐對比較法計算權重

得出評價指標的權重值后，再對各儲備備選點進行綜合評價，評價的標準分為好、一般、差三個等級，評價好的得分為2、評價一般的得分為1、評價差的不得分。例如，對8 個應急物資儲備備選點b1，b2，…，b8 進行評價，見表3。

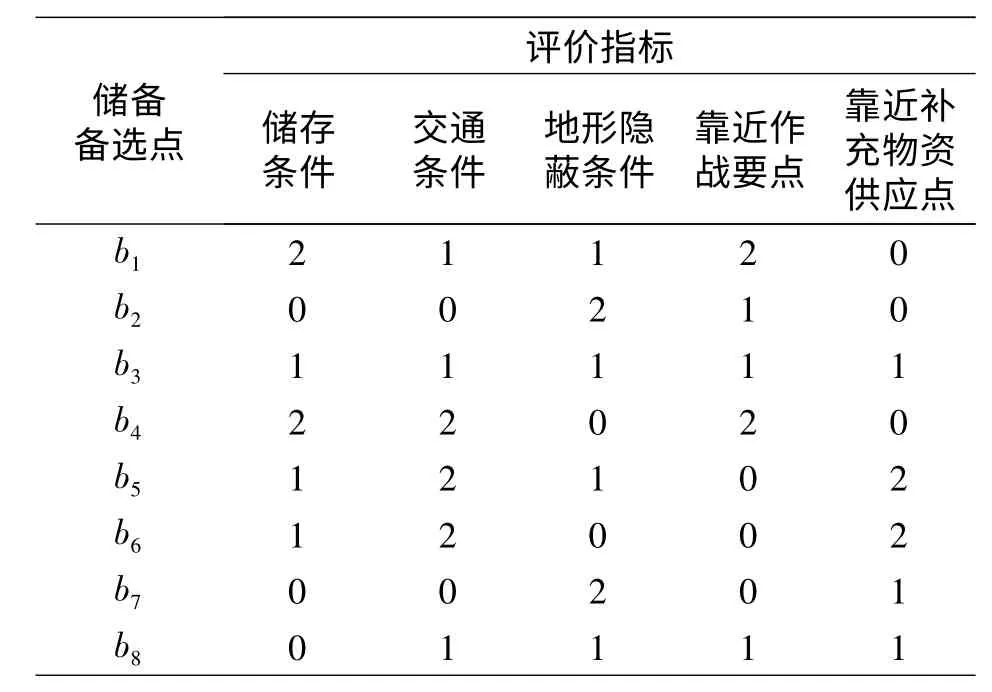
表3 備選點得分表

根據表3，各儲備點得分為:

3.3 篩選備選點

根據以上對各備選點的綜合評價，可以據此剔除一些不能滿足應急物資儲備要求的備選點，以減少后續模型計算的復雜性。如:現以評價得分1.0為劃分標準，得分大于標準的可作為備選點，低于標準的不能作為備選點。這樣，可以去掉b2、b7、b8三個不符合要求的備選點，保留剩余的五個備選點。

4 以單一目標對應急物資儲備點進行優化

在應急物資儲備點選址目標模型中，設定了最短距離、最短時間、調運成本、建設成本、儲存數量五個目標，可以任意目標進行應急物資儲備點優化。在本文中，僅以時間最短為目標進行應急物資儲備優化為例，對單一目標優化展開說明。

該優化目標是應急物資從儲備點輸送到需求點的時間最短，這需要先算出各條線路的應急物資輸送速度，再根據線路長度和平均輸送速率，折算成標準里程(通過速度一致的里程)，通過比較標準里程的長短即可比較輸送時間的長短，從而確定應急物資儲備點的位置。

4.1 運距換算

儲備點的布置，必須依托于運輸方式的選擇，無論采用何種運輸方式，前送的時間要求是一致的。根據實際情況，應急物資輸送主要有水路、鐵路、公路這三種運輸方式，其實際輸送距離的長短并不能衡量出應急物資前送實際時間長短，這就無法比較不同運輸方式條件下保障時效性的優劣。這需要結合各種運輸方式條件下應急物資輸送的速度、道路或水路的安全通過系數等因素具體分析，對實際輸送距離進行運距的換算，折算成標準運距。標準運距越長，該運輸方式下單位應急物資前送所需的時間越長，保障效益越差。設標準運距為S，實際運距為L，折算系數為d，則有S = Ld。

標準運距的折算系數d可根據下式得出:

式(2)中，V0為單位應急物資輸送的標準速度(km/h);V為該輸送方式下單位應急物資的實際運送速度(km/h);K為該輸送方式的道路(水路)的地形修正系數，K≥1;U為該方式下安全通過系數，U≤1。

假如從儲備點A到要點B的輸送過程中經過道路換乘或輸送方式轉換，則可分段求取各路段的標準運距，再求和得出總的標準運距，即:

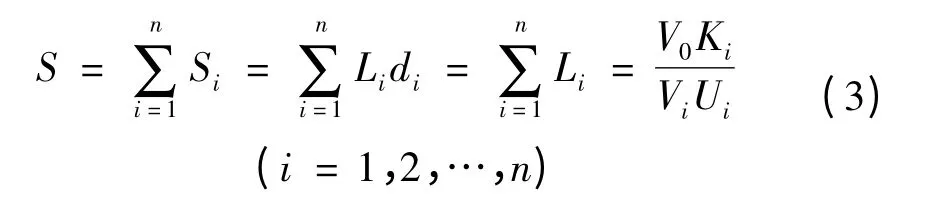
4.2 應急物資儲備優化模型的建立

最短時間優化模型，設在某一作戰方向上，作戰要點分別為ai(i =1，2，…，n)，每個要點針對某一種物資的作戰應急物資需求量分別為Yi(i =1，2，…，n)，則由選定的x個應急物資儲備點bj(j =1，2，…，x)向作戰要點運送應急物資，將實際運距進行標準運距折算后，用最短路方法計算后，設最小標準運距為Sji(i =1，2，…，n;j =1，2，…，x)，寫成矩陣形式為:

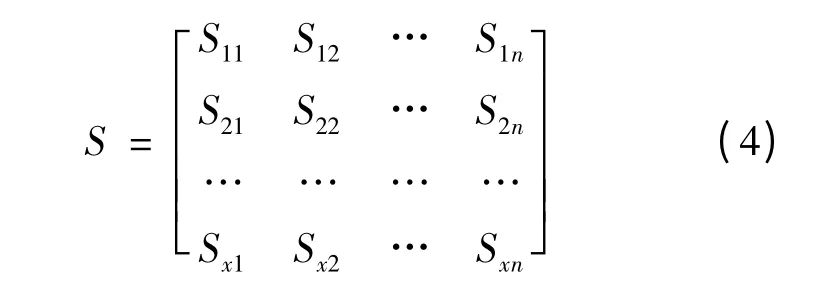
也可寫成時間矩陣形式，即標準運距除以標準運送速度:

在該矩陣中，如果某一儲備點不能到達某一需求點，可以設該段距離(時間)為∞，以簡化矩陣。

4.3 儲備方案分析

在上述矩陣中，可以很快找到一個儲備點，使其到最遠需求點的標準運距最短(時間最短)，該點即是所求的最優點。但這里的最優點是到最遠需求點的標準運距最小，而不是總標準運距最小。也就是，到最遠需求點的時間最少，而不是總時間最少。優化比較時，先從矩陣中提取每個儲備點到所有需求點中的最大標準運距(時間)，再比較每個儲備點的最大標準運距(時間)，選出標準運距最短(時間最少)的儲備點。

如果需要確定多個儲備點，則應根據需要確定的儲備點個數，選取儲備點組合，使得該儲備點組合能到達所有需求點。該組合中，按照就近保障的原則，以組合中儲備點到需求點標準運距(時間)最小來確定保障關系，再比較不同組合到最遠需求點的最大標準運距(時間)，用時少者為最優。通過儲備點組合之間的比較，可以得到最優的儲備點方案。

4.4 應用舉例

設在位置點b1、b2、b3、b4、b5中設置應急物資儲備點，要保障作戰方向上的7 個要點(a1，a2，…，a7)，各要點的應急物資需求量分別為Y1，Y2，…，Y7，儲備點經通道至作戰要點的最短時間(h)矩陣如下:

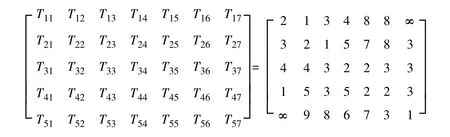
可以假設儲備點至需求點的時間不能長于5h，即從儲備點到保障要點的時間Tji≤5h，如果Tji ＞5h，則該儲備點不能保障這個需求點。那么，時間矩陣可變為:

4.4.1 選擇一個儲備點

如果只選擇一個儲備點(能到達所有需求點)，則從矩陣中選出至最遠保障點時間最短的一個點。矩陣中點b3至最遠需求點的時間為4h，點b4至最遠需求點的時間為5h，b3點應是時間最優的儲備點。

4.4.2 選擇兩個以上儲備點

如果選擇兩個以上的儲備點，則要根據就近保障的原則區分保障任務。本文中，以選擇兩個儲備點為例，可以選擇的位置點組合有:b1和b3、b1和b4、b2和b3、b2和b4、b3和b4、b4和b5。

(1)當選擇b1和b3為儲備方案時，由b1保障a1、a2、a3，至最遠需求點時間為3h;由b3保障a4、a5、a6、a7，至最遠需求點時間為3h;該方案至最遠需求點的時間為3h。

(2)當選擇b1和b4為儲備方案時，由b1保障a2、a3、a4，至最遠需求點時間為4h;由b4保障a1、a5、a6、a7，至最遠需求點時間為3h;該方案至最遠需求點的時間為4h。

(3)當選擇b2和b3為儲備方案時，由b2保障a1、a2、a3、a7，至最遠需求點時間為3h;由b3保障a4、a5、a6，至最遠需求點時間為3h;該方案至最遠需求點時間為3h。

(4)當選擇b2和b4為儲備方案時，由b2保障a2、a3、a4、a7，至最遠需求點時間為5h;由b4保障a1、a5、a6，至最遠需求點時間為2h;該方案至最遠需求點時間為5h。

(5)當選擇b3和b4為儲備方案時，由b3保障a2、a3、a4、a5，至最遠需求點時間為4h;由b4保障a1、a6、a7，至最遠需求點時間為3h;該方案至最遠需求點時間為4h。

(6)當選擇b4和b5為儲備方案時，由b4保障a1、a2、a3、a4、a5、a6，至最遠需求點時間為5h;由b5保障a7，至需求點時間為1h;該方案至最遠需求點時間為5h。

所以，當選擇b1和b3或b2和b3為儲備方案時，至最遠儲備點所花時間最短，它們是時間最優的儲備方案。

5 以多目標決策方法進行應急物資儲備優化

在實際應用中，物資儲備點組合方案的選取標準不一，究竟該以哪一種目標作為最終的選取標準很難確定。不同優化目標方案之間往往會相互矛盾，如:距離前方近勢必距離后方油源遠，減少儲備點勢必造成單個儲備點數量規模過大，等等。可考慮采用多目標決策方法，綜合考慮物資儲備點距離、時間、調運成本、建設成本、儲備數量等因素，賦予不同的加權系數，比較得出物資儲備優化方案。

5.1 建立模型

首先明確評價目標和建立評價指標，評價指標可以通過專家打分、綜合評議的方式確立;備選方案可以通過決策者與相關專家會審確定。

5.2 統一標準

不同評價目標的計量單位標準不一，有距離、時間、成本、數量等，無法進行比較。因此，必須把這些計量單位數值轉化為可比較的效用值來表示。效用值取0—1 之間的所有數，每個目標的最壞程度，效用值為0，低于最壞程度的舍棄;每個目標要求的最好程度，效用值取1，高于最好程度的同最好程度一樣看待，取值為1。

為便于保障，利于安全，假設儲備方案的幾個目標應為:距需求點距離最好小于200km，最壞也不能超過500km;到需求點時間最好在12h 內，最壞也不能超過24h;物資調運總成本最好在3000 噸·百公里以下，最壞也不能超過6000 噸·百公里;物資儲備點建設成本最好在5000 萬元以下，最壞也不能超過6000 萬元;物資儲備總數量最好在1 萬噸以下，最壞也不能超過2 萬噸。這樣可以畫出各目標的效用曲線，并求得各方案中各目標的效用值大小。

5.3 淘汰劣案

作為備選方案，所有目標只要有一項是超出最壞程度的，作為劣案淘汰。

5.4 附加系數

在上述目標中，并不是所有的目標都具有同等重要性，因此需要考慮各個目標在優化中的重要程度并賦予適當的系數。將各方案目標的效應值乘以比重系數，然后相加得到總和，方案所得總和最大的就是最優方案。即:

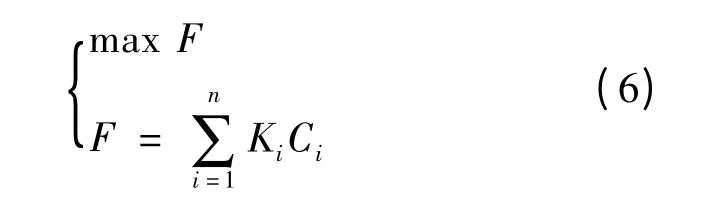
式(6)中，F為效用值函數，Ki為每個目標的效用值比重系數，Ci為評價目標。

5.5 應用舉例

假設有儲備布局方案P1、P2、P3，綜合最短距離、最少時間、最小調運成本、最小建設成本和最少儲存數量等優化目標進行物資儲備的比較優化，五個優化目標的比重系數分別為2、3、3、1、1，三個儲備方案的目標值見表4。

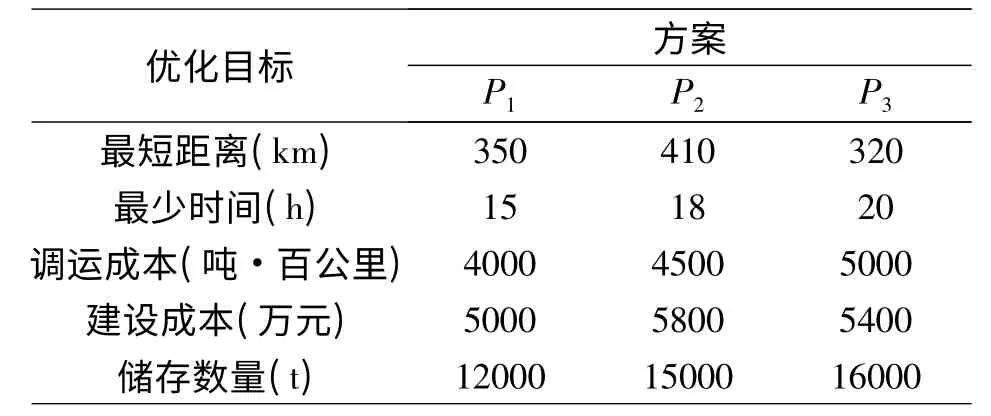
表4 儲備布局方案目標值對比表

根據前文所設的效用值程度，進行效用值計算后所得見表5。

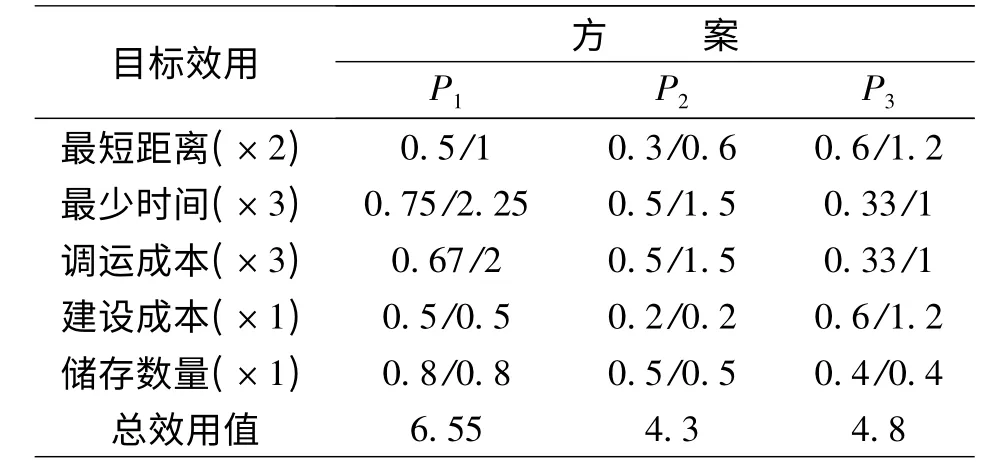
表5 儲備布局方案效用值對比表

從表5 中可以看到，當采用方案P1時，多目標效用值最大，即取得最優的儲備效能。所以多目標決策的優化結果是選擇方案P1。

6 結束語

在應急物資儲備點選址問題研究中，由于不同優化目標可能存在矛盾，一般沒有全局最優解存在。本文建立的多目標優化模型，利用模糊邏輯的多目標遺傳算法求解，能夠達到比較好的效果。該模型曾被應用于部隊軍需物資油料保障系統中，可根據標定的保障方向、選擇的參與保障單位、初始的保障任務以及用戶設定的相關參數等，對軍區油料儲備布局進行優化分析，為戰區的平時供應管理和戰時保障的保障點選址提供決策參考，取得很好的軍事和經濟效益。

［1］ 張來順，尚振峰，姚頔.聯勤保障一線倉庫布局優化分析［J］.火力與指揮控制，2011，36(1):37 -39.

［2］ 陳陽，雍岐東，邢兆勇，等.基于物聯網的軍隊油料儲備布局研究［J］.訓練與科技，2013，34(3):4 -6.

［3］ 陳智，郭繼坤.以線性規劃方法構建油料儲備布局模型［J］.后勤學術，2004(12):90 -92.

［4］ 雙海軍.戰備物資儲備優化［D］.重慶:后勤工程學院，2001.

［5］ 徐東.新形勢下軍事物資儲備布局的合理性研究［D］.北京:后勤指揮學院，1999.

［6］ 郭繼坤.戰時物資勤務［M］.北京:軍事科學出版社，2004.