基于改進PSO算法的水輪機PID調(diào)速器的參數(shù)設(shè)計

汪醒鵬

（湖南省水利水電科學研究所 長沙市 410007）

范 哲

（益陽市柘溪水電站 益陽市 413500）

水輪發(fā)電機組承擔著將水能轉(zhuǎn)化為旋轉(zhuǎn)機械能，再將旋轉(zhuǎn)機械能轉(zhuǎn)化為電能的任務。與風能、水能、熱能相比，電能對存儲運送介質(zhì)有特殊要求，電能不能大量存儲，因此電能的生產(chǎn)和消費必須同時進行。GB/T 15945-2008[1]中規(guī)定：電力系統(tǒng)正常頻率范圍為50±0.2 Hz，頻率偏差過大不僅直接影響發(fā)電機組自身穩(wěn)定運行，造成電網(wǎng)解列，而且導致以電動機為動力設(shè)備的生產(chǎn)制造廠家產(chǎn)生大量廢品。因此，水輪機調(diào)節(jié)系統(tǒng)必須根據(jù)用戶負荷的變化不斷調(diào)節(jié)水輪發(fā)電機的輸出功率，水輪機調(diào)節(jié)系統(tǒng)的優(yōu)劣性決定電能品質(zhì)。水輪發(fā)電機PID 調(diào)速器參數(shù)優(yōu)化的方法有：下降梯度法[2]、神經(jīng)網(wǎng)絡[3]、遺傳算法[4]、模擬退火算法[5]等，這些方法對提高PID 調(diào)速器的調(diào)節(jié)品質(zhì)均有重要的理論價值，但是下降梯度法要求提取精確的函數(shù)，處理能力有限；神經(jīng)網(wǎng)絡易于陷入局部最優(yōu)；GA 算法進化速度慢，易于早熟。PSO 算法[6]具有并行處理、尋優(yōu)效率高的特點，與結(jié)構(gòu)簡單、魯棒性強的PID 調(diào)速器相適應。

基本粒子群算法在處理水輪機PID 調(diào)速器時會出現(xiàn)局部最優(yōu)或收斂緩慢等問題，因此本文提出了一種改進的自適應PSO 算法，該算法根據(jù)函數(shù)尋優(yōu)策略改進慣性權(quán)重對搜索能力的影響，提高求解精度并加快收斂速率。在此基礎(chǔ)上引入微分進化算子[7]選取部分隨機粒子進行變異處理，從而提高了種群的多樣性，擴大搜索解空間的區(qū)域，避免早熟和局部最優(yōu)，并利用matlab 對該模型進行仿真優(yōu)化，仿真結(jié)果驗證了該方法的正確性和有效性，為水輪機調(diào)節(jié)系統(tǒng)提供一種可行的控制方案。

1 水輪機調(diào)節(jié)控制系統(tǒng)matlab模型

水輪機控制系統(tǒng)主要由PID 控制模塊和水輪機被控模塊組成，控制模塊[8]系統(tǒng)結(jié)構(gòu)在matlab 建立如圖1 所示模型。其中，控制模塊中的Kp、Ki、Kd 為simulink 系統(tǒng)中的待優(yōu)化參數(shù)，分別表示比例常數(shù)、積分常數(shù)和微分常數(shù)。被控模塊Subsystem 中封裝了水輪機調(diào)速系統(tǒng)被控對象，包括機械液壓子模塊[9]（MHS）、水輪機及引水系統(tǒng)子模塊[10]（WDS）和發(fā)電機及負荷子模塊[11]（GS）。Subsystem 模塊、MHS 模塊、WDS 模塊、GS 模塊的matlab 建模分別如圖2、圖3、圖4 和圖5 所示。

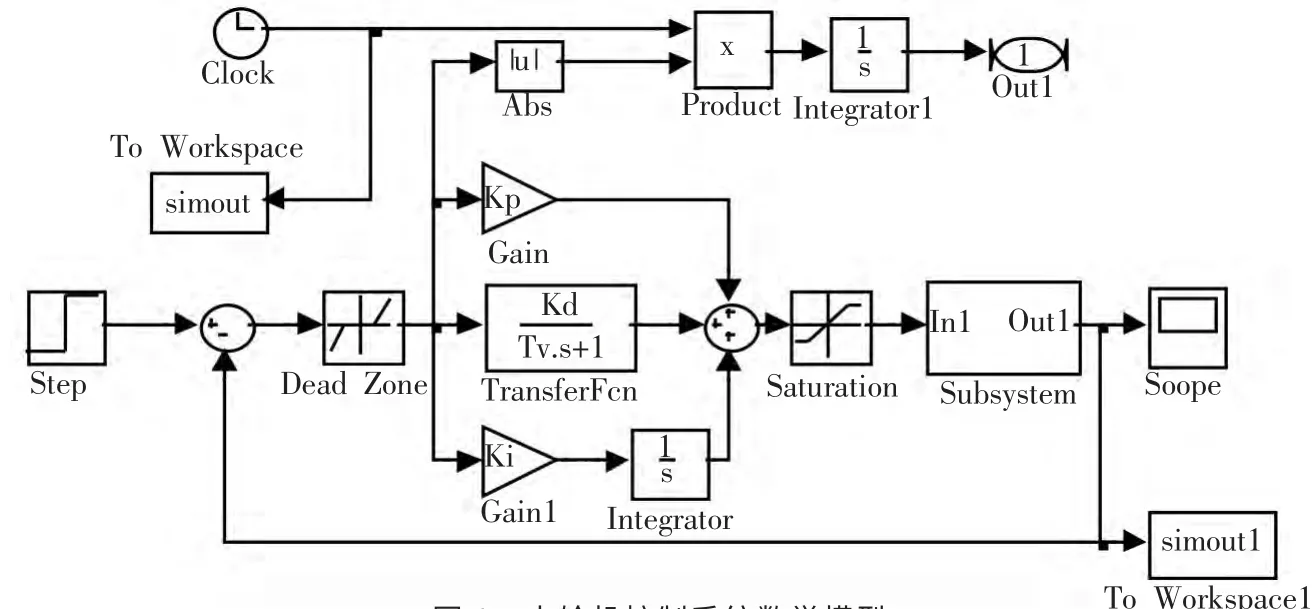
圖1 水輪機控制系統(tǒng)數(shù)學模型

圖2 水輪機調(diào)節(jié)系統(tǒng)被控模塊

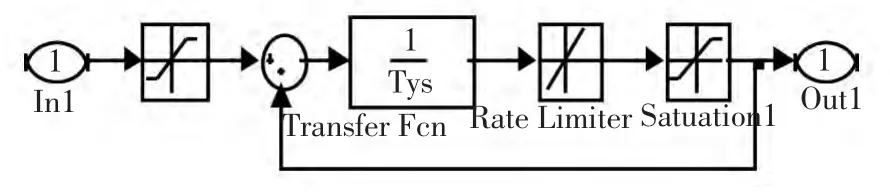
圖3 機械液壓模塊MHS

圖4 水輪機及引水系統(tǒng)模塊WDS

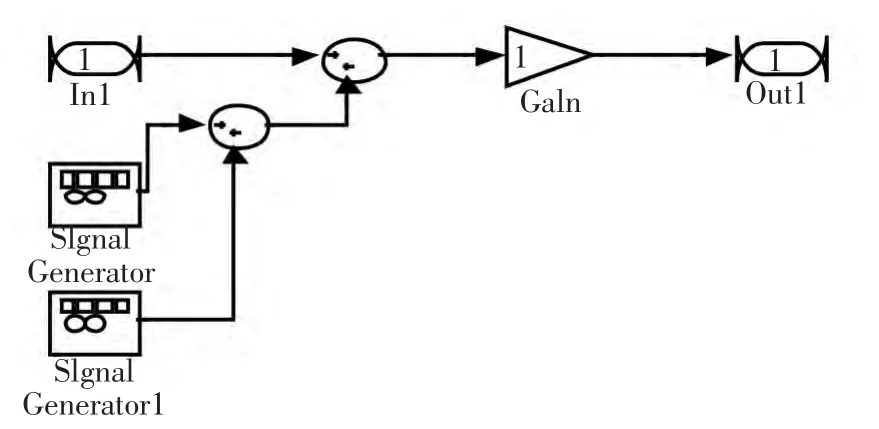
圖5 發(fā)電機及負荷模塊GS

2 改進的PSO優(yōu)化算法

2.1 基本PSO 優(yōu)化算法

與魚群算法、Ant 算法相同，PSO 算法是從生物群體智能獲得啟示，利用并行計算的智能優(yōu)化方法。Kennedy 和Eberhart 在研究鳥類捕食過程時，模擬其搜索解區(qū)域方式，將粒子抽象為潛在解，使每個粒子綁定一個適應度函數(shù)來決定其適應度值。粒子的速度決定粒子移動的方向和距離，速度隨自身及其他粒子的移動經(jīng)驗進行動態(tài)調(diào)整，從而實現(xiàn)個體在可解空間中的尋優(yōu)。粒子在求解空間中運動，通過追蹤個體極值Pbest 和群體極值Gbest 更新個體位置。

基本粒子群算法思路： 存在一個n 維解區(qū)域搜索空間，隨機分布m 個粒子(X1，X2,……,Xm),每個粒子均代表該空間中可能解，數(shù)學描述為n 維向量Xi=（Xi1，Xi2，……,Xin），根據(jù)計算每個Particle 的個體極值Pid=(Pi1,Pi2,……,Pin)與全體極值Pg=(Pg1,Pg2,……,Pgn), 利用速度調(diào)整公式實時跟新自身位置最終找出最優(yōu)解。速度調(diào)整公式為：

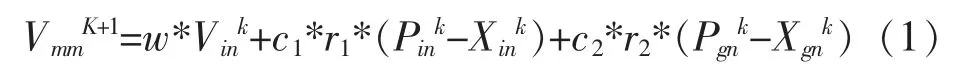
式中c1和c2取[0,2]，r1和r2為程序自動隨機數(shù)。

自身位置更新公式為：

基本粒子群算法參數(shù)依賴性小，計算效率高，但是在求解水輪機PID 調(diào)速器這類復雜模型過程中，易出現(xiàn)早熟和局部收斂，導致所得結(jié)果精度較低或者收斂速度過慢。

2.2 改進的PSO 優(yōu)化策略

（1）自適應權(quán)重因子調(diào)整策略。

從基本粒子群算法速度調(diào)整公式可以看出，權(quán)重因子w 直接影響速度梯度，從而控制當前粒子在n 維空間中搜索解的能力。若w 數(shù)值偏小，粒子的記憶能力差，粒子移動緩慢，降低求解效率，若w 數(shù)值偏大，步長變大，利于搜索全體空間，但精度降低，不利于求得最優(yōu)解，因此本文將采用一種自適應調(diào)整權(quán)重因子的方法，其表達式為：

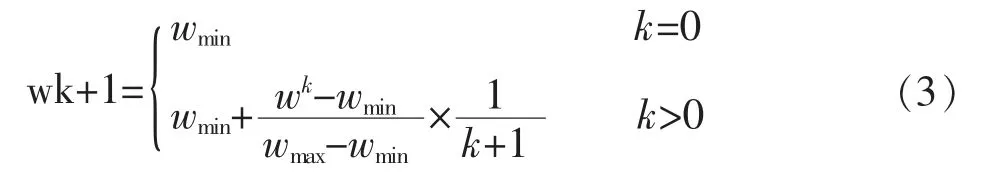
式中 k，k+1 表示循環(huán)迭代次數(shù)，大量試驗經(jīng)驗表明：Wmin取0.85，Wmax取2.2 時，收斂速度快，所求精度高。

通過限定權(quán)重因子的最小值并引入迭代次數(shù)增強其自適應能力后，在算法尋優(yōu)前期，權(quán)重因子偏大，步長大，擴展搜索全域的能力，加快收斂速度。在尋優(yōu)后期，權(quán)重因子偏小，利于在最優(yōu)解附近微調(diào)整，從而利于調(diào)整精度。

（2）微分進化調(diào)整策略。

執(zhí)行新的權(quán)重因子更新公式的同時，引入微分進化操作，在每一代的粒子中隨機選取部分個體，進行變異進化，公式為：

式中 k，k+1——粒子進化代數(shù)；

F——向量差分因子，其大小控制粒子的放大系數(shù)，本文取0.9。

2.3 改進PSO 算法的適應度函數(shù)

傳統(tǒng)的PSO 算法優(yōu)化水輪機PID 調(diào)速器參數(shù)中，引用時間絕對誤差乘積指標ITAE 指標作為粒子的適應度函數(shù)，其表達式為：

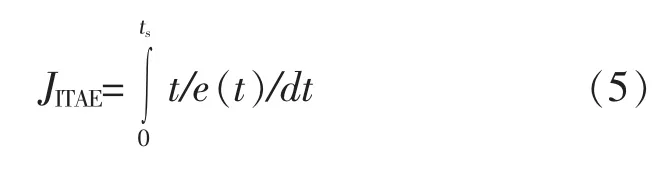
式中 t——時間；

ts——積分時間上限；

e（t）——誤差。

為保證水輪機調(diào)速控制器具有滿意的動態(tài)響應的特性，本文在ITAE 的基礎(chǔ)上，綜合考慮最大轉(zhuǎn)速偏差相對值Xmax及控制量平方的積分，使用帶加權(quán)系數(shù)的ITAE 作為粒子的適應度函數(shù)，其表達式為：

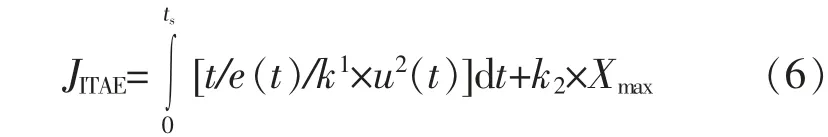
3 matlab中算法執(zhí)行過程

在matlab 的simulink 模塊建立本文圖1～圖5所示數(shù)學模型，在M 文件中編寫改進PSO 算法程序，二者交互過程如圖6 所示。

改進PSO 算法優(yōu)化水輪機PID 調(diào)速器算法步驟如下：

①以隨機方式賦值給每個Particle 原始位置和原始速度。②根據(jù)適應度函數(shù)計算出粒子適應度值。③將每個粒子的適應度值與其歷史位置對比，優(yōu)異者作為Pbest。④將粒子的適應度值與整個粒子群的最優(yōu)歷史位子作對比，優(yōu)異者作為整個粒子群的Gbest。⑤根據(jù)式（1）和式（3）更新每個Particle 的移動方向和速度。根據(jù)式（2）更新粒子當前位置。⑥根據(jù)式（4）隨機選取部分粒子進行變異操作。⑦根據(jù)式（6）輸出性能指標，若滿足條件跳出循環(huán)，否則轉(zhuǎn)第②步。

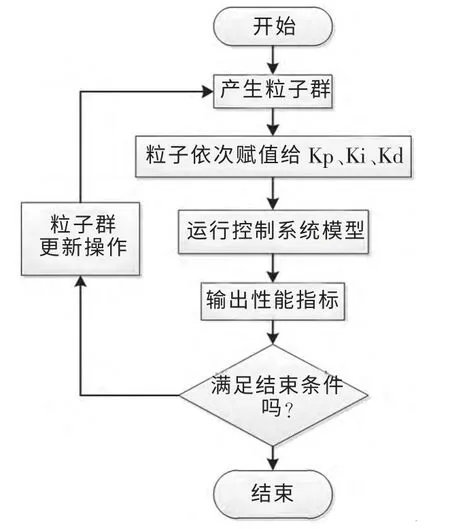
圖6 算法流程圖

4 工程實例分析

4.1 計算數(shù)據(jù)

已知湖南農(nóng)村某小水電站1#混流式水輪機裝機容量700 kW，額定水頭97.9 m，最小水頭96 m，最大水頭99 m，額定流量0.71 m3/s，額定轉(zhuǎn)速1 000 r/min，采用單機孤網(wǎng)帶負荷模式運行。改進PSO 算法的試驗參數(shù)設(shè)置范圍如本文2.1，2.2，2.3 所述。

4.2 空載工況

將模型置于空載條件下，對試驗仿真機加5%的頻率擾動，研究機組轉(zhuǎn)速過渡過程，其轉(zhuǎn)速偏差結(jié)果如圖7 所示: 藍紅線分別代表機組經(jīng)過改進PSO算法優(yōu)化前后的轉(zhuǎn)速響應曲線，經(jīng)過改進PSO 算法優(yōu)化過的水輪機PID 調(diào)速器響應曲線超調(diào)量大幅度減小，調(diào)整時間也一半，整個過程有明顯改進。機組輸出性能指標結(jié)果如圖8 所示：ITAE 進入穩(wěn)定的時間加快，且穩(wěn)定值下降幅度較大。

為驗證改進權(quán)重慣性因子對PSO 算法的影響，將改進PSO 算法與基本PSO 算法的尋優(yōu)收斂曲線進行對比，結(jié)果如圖9 所示：在迭代次數(shù)小于20 時，紅色收斂曲線的下降幅度大于藍色線，說明在算法早期，改進PSO 算法收斂速度較快，當?shù)螖?shù)大于20 時，紅色收斂曲線線不斷作微調(diào)整，說明改進PSO 算法精度作微調(diào)整。試驗結(jié)果與權(quán)重慣性因子特性相吻合。

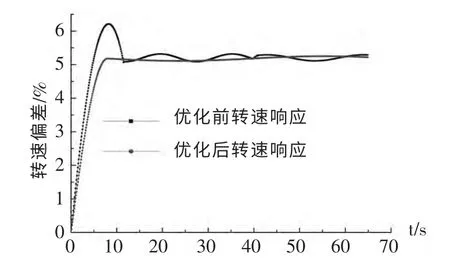
圖7 轉(zhuǎn)速偏差結(jié)果

圖8 機組輸出性能指標結(jié)果

圖9 尋優(yōu)收斂曲線對比圖

圖10 10%試驗負載下轉(zhuǎn)速偏差結(jié)果

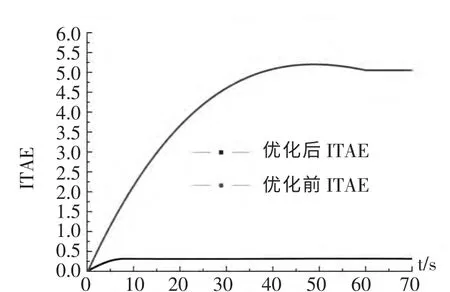
圖11 輸出特性指標

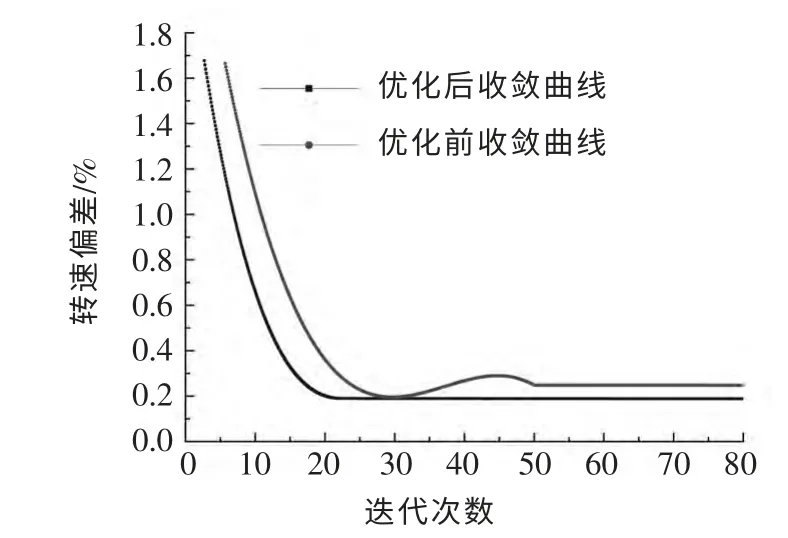
圖12 尋優(yōu)收斂曲線對比圖

4.3 負荷工況

為研究水輪機調(diào)節(jié)的動態(tài)特性，將機組置于10%試驗負荷下，其機組轉(zhuǎn)速偏差結(jié)果和輸出特性指標ITAE 分別如圖10，圖11 所示，結(jié)果表明：經(jīng)過PSO 算法優(yōu)化過的PID 水輪機調(diào)速器在孤網(wǎng)10%負荷擾動下，機組轉(zhuǎn)速偏差的過渡過程比未經(jīng)優(yōu)化的機組過渡過程有明顯改進；超調(diào)量減少、調(diào)節(jié)時間縮短、機組轉(zhuǎn)速偏差的ITAE 指標下降。

同理，將改進PSO 算法與基本PSO 算法的尋優(yōu)收斂曲線做比較，結(jié)果如圖12 所示:在整個過程中，兩種算法的調(diào)準精度相差較小，但改進PSO 算法的收斂速度較快。優(yōu)化性能較好。

5 結(jié) 論

為了提高傳統(tǒng)PSO 算法對PID 型水輪機調(diào)速器Ki,Kp,Kd 三個參數(shù)的優(yōu)化質(zhì)量，本文選擇自適應調(diào)整權(quán)重慣性因子，該方法綜合考慮了實際粒子群算法迭代過程中的收斂步長，平衡收斂速度和精確度的影響，避免陷入局部最優(yōu)的同時提高了計算效率，同時引入微分進化因子，增加了全局搜索能力，確保了迭代過程中出現(xiàn)結(jié)果接近而早熟，最后通過5%頻率擾動機組仿真試驗和10%負荷擾動試驗證明了改進PSO 算法優(yōu)于基本PSO 算法，經(jīng)過改進PSO 算法優(yōu)化過的PID 調(diào)速器也具有較好的性能。

[1] 程遠楚，張江濱.水輪機自動調(diào)節(jié)[M].北京：中國水利水電出版社，2010.

[2] 湯儀平，金福江. 最速下降法和共軛梯度的混合算法及全局收斂[J]. 華僑大學學報（自然科學版），2007，（2）:124-126.

[3] 侯樹文，王琳琳，盧家濤，等. BP 網(wǎng)絡模糊PID 控制在水輪機調(diào)速器中的應用[J]. 人民長江，2008，39（2）: 79-80.

[4] 孫美鳳，張永華，張俊紅. 水輪機調(diào)速器參數(shù)自整定遺傳算法的研究[J]. 水力發(fā)電，2007，（5）.

[5] 王勇，劉厚林，袁壽其，等.離心泵非設(shè)計工況空化振動噪聲的試驗測試[J]. 農(nóng)業(yè)工程學報，2012，28（2）：35-38.

[6] 魚瑞文，周佩華，錢苗旺，等. 基于模糊復合最優(yōu)粒子群算法的礦用電機控制系統(tǒng)參數(shù)優(yōu)化[J]. 煤礦機械，2012，33（3）.

[7] 劉自發(fā)，張建華. 一種求解電力經(jīng)濟負荷分配問題的改進微分進化算法[J]. 中國電機工程學報，2008，（10）:100-105.

[8] 魏守平.水輪機調(diào)節(jié)系統(tǒng)仿真[M].武漢：華中科技大學出版社，2011.

[9] 魏守平.水輪機調(diào)節(jié)系統(tǒng)的MATLAB 仿真模型[J]. 水電自動化與大壩監(jiān)測，2009，（4）.

[10] 曹程杰，莫岳平，劉丹丹. 基于改進遺傳算法的水輪機PID 調(diào)速器最優(yōu)參數(shù)整定[J].微計算機信息，2009，（34）.

[11] 羅旋，魏守平.基于MATLAB 的水輪機調(diào)節(jié)系統(tǒng)仿真[J].西北水電，2005，（3）.