卷揚式啟閉機卷筒組結構優化設計

吳文龍（安徽省水利水電勘測設計院 合肥 230088）

科技論壇

卷揚式啟閉機卷筒組結構優化設計

吳文龍
（安徽省水利水電勘測設計院 合肥 230088）

我國正處于高速發展時期，各行各業都有大量工程需要建設、設備需要制造，設計人員在確保設計產品滿足各種規范要求、能夠安全可靠運行的前提下，還要千方百計地使產品節省建材，經濟合理，節能環保。本文以水利工程常用的卷揚式啟閉機卷筒組結構作為優化設計的切入點，介紹了一般工程、設備設計的優化方法。

啟閉機 卷筒組 優化設計 目標函數 設計變量

1 引言

卷揚式啟閉機是廣泛運用的一種水利工程閘門起吊設備，其主體僅為一般起重機械的一個起升機構，由驅動裝置、傳動裝置、卷筒組部件、鋼絲繩、吊物裝置及制動裝置等組成。卷筒組部件則由大齒輪、小齒輪、軸、卷筒等構成，是決定卷揚式啟閉機機身重量的主要部件。傳統的設計方法是依據經驗選取或計算各部位尺寸，然后進行強度復核，很難做到用材最省。因此，在滿足啟閉機生產工藝、結構安全、使用可靠的前提下，對卷筒組各部位尺寸進行優化設計，可以有效地降低啟閉機的機重和造價。卷揚式啟閉機主體結構示意圖見圖1。

2 建立數學模型

2.1 建立目標函數

建立一個適當的目標函數來評價設計方案的優劣程度，是機械優化設計的首要問題。對于一般的起重機構來說，應以體積小、重量輕、效率高、造價省為目標。目標函數越多，優化設計越趨完善，但其難度也相應增加。因此，一般不宜取過多目標函數。本文所介紹的優化設計的目標函數是啟閉機卷筒組三個主要部件的重量之和。

F（X）=W1（X）+W2（X）+W3（X）

式中，W1（X）、W2（X）、W3（X）分別為大齒輪、卷筒、卷筒軸3個部件的重量相對于設計變量的函數表達式，限于篇幅，不再贅述。

2.2 確定設計變量

優化設計常選取對目標函數有顯著影響的獨立參數作為設計變量。大齒輪、小齒輪（重量可或略不計）主要取決于齒寬、模數和分度圓直徑，而分度圓直徑又與小齒輪齒數、模數及傳動比有關，因此，把齒寬b、模數m、小齒輪齒數Z1、傳動比i等4個參數作為設計變量。至于大齒輪齒數、分度圓直徑、幅板厚度、齒圈厚度、輪轂厚度及寬度等要素均可根據齒輪的傳統設計方法擬為上述4個變量的函數或定值。卷筒的重量主要取決于卷筒直徑、長度和壁厚3個參數，在鋼絲繩規格、起升高度確定的情況下，卷筒長度是其直徑的一個參數，可見，只要把卷筒直徑D、卷筒壁厚δ作為設計變量就能控制卷筒的重量。已知卷筒直徑還可相應確定大齒輪與卷筒連接的止口內外徑。卷筒軸的重量主要取決于軸徑和軸的長度，軸長與卷筒長度、大齒輪寬度以及選定的軸承支承的軸頸長度有關，所以只要把軸徑d作為設計變量，便能計算出軸的重量。另外，軸徑d對大齒輪的輪轂寬度、卷筒的兩端孔徑也有影響。

上述7個相互獨立的設計變量（在應用中，用戶可根據需要增減一些變量）可有效控制卷筒組部件重量的優化問題。其排列如下：

X=（x1，x2，x3，x4，x5，x6，x7）T=（i，Z1，m，D，δ，d，b）T

在這7個設計變量中，i，D，δ，d，b均為連續變量，而模數m有其規定的系列，屬離散變量，小齒輪齒數是整形變量。在優化設計過程中，可將離散變量和整形變量均當作連續變量進行優化，待得出結果后，進行圓整，圓整后的各變量也必須滿足各項約束條件。

2.3 選取約束條件

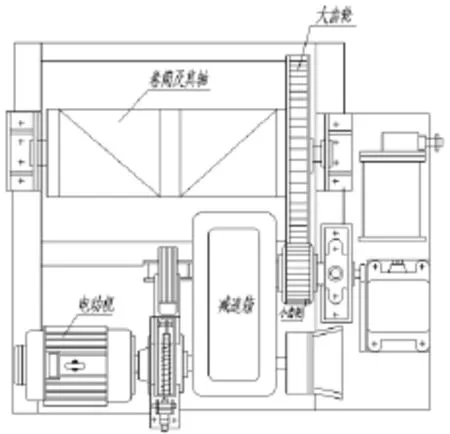
圖1 卷揚式啟閉機主體結構示意圖

卷筒組約束條件通常包括剛度、強度、運動學、動力學、工藝、幾何安裝等，根據現行的卷揚式啟閉機設計規范和理論，選取合理的卷筒組重量優化設計約束條件如下：卷筒最小直徑約束、卷筒最小壁厚約束、卷筒抗壓強度約束、卷筒抗拉強度約束、卷筒抗壓穩定性約束、啟閉速度上下限約束、電機功率約束、齒寬系數上下限約束、小齒輪不發生根切約束、開式齒輪傳動比約束、齒面接觸強度約束、齒根彎曲強度約束、鋼絲繩偏角約束、安裝尺寸約束、卷筒軸強度約束。

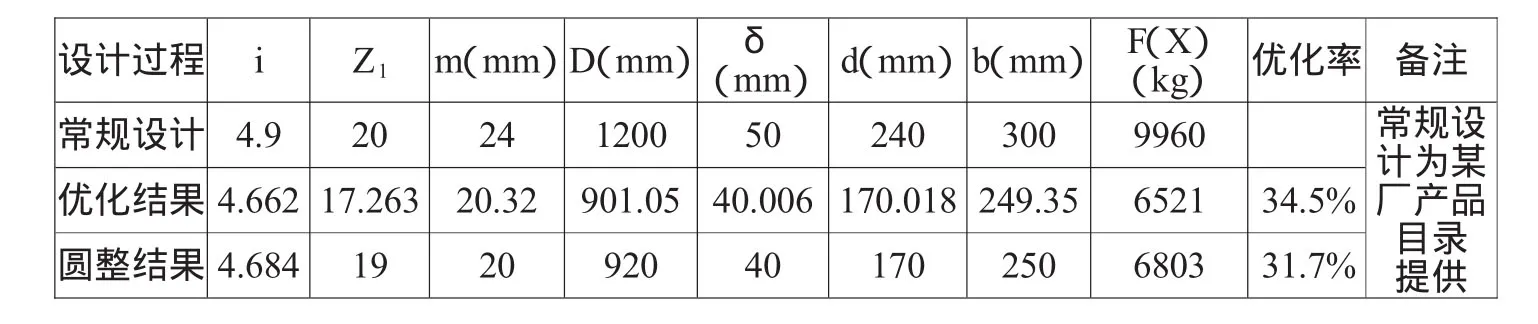
表1 常規設計與優化設計成果對比表

3 選擇優化方法

3.1 有約束優化方法選擇

卷揚式啟閉機卷筒組結構優化設計是一個非線性數學模型，為了提高計算效率，并能達到一定的收斂精度，選擇內點形式的混合罰函數法，即把有約束優化問題演變成一個無約束優化問題加以解決。用混合罰函數法求解時，其懲罰函數由原目標函數和包含約束函數的懲罰項組成：

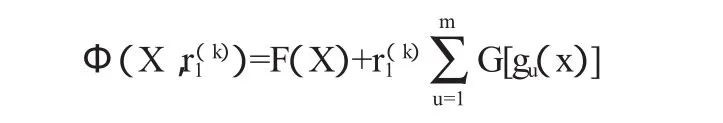
式中：F（X）—目標函數；

G[gu（x）]—不等式約束函數的懲罰項，G[gu（x）]= [gu（x）]-1；

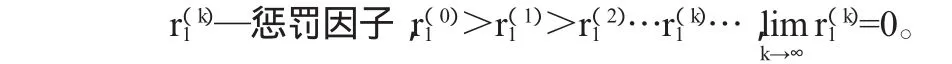
3.2 無約束優化方法選擇

通過懲罰函數的處理后，有約束求優問題已變成一個無約束求優問題。無約束求優方法很多，因數學模型非線性程度較高，為避免求導，選擇鮑威爾（Powell）法。為防止鮑威爾法中出現“退化”現象，應對新生搜索方向組進行判別。3.3一維優化方法選擇

在鮑威爾法無約束求優運算過程中，最終尋優方法還是要進行一維搜索。一維搜索的方法也很多，為便于計算，可利用一個二次插值多項式P（X）來代替原目標函數，然后求出該多項式的極值，以此作為目標函數F（X）的近似極值。經過反復試算，縮小搜索區間，最終取得目標函數極值。

3.4 優化結果圓整

計算機輸出的最優結果一般為小數點后的數字很長的數值，在機械制造中無法實現，再加上小齒輪齒數是整形變量，不能有小數，齒輪模數m屬離散變量，須符合規定的系列值，因此，必須對計算機輸出的各設計變量進行圓整。圓整的準則是：各設計變量盡可能接近優化結果值。圓整后的變量值必須使得各約束條件成立，這一步工作也可以利用計算機進行驗證。

4 實例

某工程需要設計一臺額定起升荷載為2000kN，最大起升高度為14m，起升速度為1.5～1.6m/min的卷揚式啟閉機。

常規設計可以初擬出各部件的結構尺寸和有關參數（包括上述7個設計變量），并可計算出卷筒組各部件的重量之和，在常規設計的基礎上，對卷筒組進行優化設計，得出優化結果，最后進行圓整復核。常規設計與優化設計成果對比情況見表1。

從表1可以看出，優化率達到百分之三十多，顯然，在卷揚式啟閉機設計中，對卷筒組結構優化設計可以創造良好的經濟效益