線性規(guī)劃的教學(xué)模式探討
苗連英 逄世友


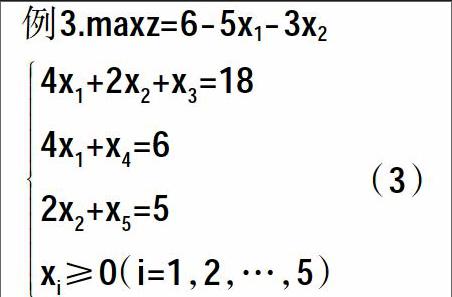
摘要:線性規(guī)劃是運(yùn)籌學(xué)的核心內(nèi)容,求解線性規(guī)劃的單純形法在理論上已趨于成熟,應(yīng)用也越來(lái)越廣泛。為了使學(xué)生更容易、更深刻地理解這種算法及其理論基礎(chǔ),本文給出了一種循序漸進(jìn)的教學(xué)模式。這種模式也適用于運(yùn)籌學(xué)其他內(nèi)容的教學(xué)。
關(guān)鍵詞:?jiǎn)渭冃畏ǎ谎驖u進(jìn);教學(xué)模式
中圖分類號(hào):G642.0 文獻(xiàn)標(biāo)志碼:A 文章編號(hào):1674-9324(2014)45-0036-04
運(yùn)籌學(xué)是二戰(zhàn)期間發(fā)展起來(lái)的一門應(yīng)用學(xué)科,它廣泛應(yīng)用現(xiàn)有的科學(xué)技術(shù)知識(shí)和數(shù)學(xué)方法,解決實(shí)際中提出的一些問(wèn)題,為決策者選擇最優(yōu)策略提供定量依據(jù),其內(nèi)容包括:規(guī)劃論(線性規(guī)劃、非線性規(guī)劃、整數(shù)規(guī)劃、動(dòng)態(tài)規(guī)劃、多目標(biāo)規(guī)劃等)、圖論與網(wǎng)絡(luò)分析、對(duì)策論、排隊(duì)論、存儲(chǔ)論、決策論、排序與統(tǒng)籌方法等[1]。運(yùn)籌學(xué)的實(shí)際應(yīng)用涉及生產(chǎn)計(jì)劃、運(yùn)輸問(wèn)題、人事管理、庫(kù)存管理、市場(chǎng)營(yíng)銷、財(cái)務(wù)和會(huì)計(jì)等方面。另外,還應(yīng)用于設(shè)備維修、更新和可靠性分析,項(xiàng)目的選擇與評(píng)價(jià)、工程優(yōu)化設(shè)計(jì)、環(huán)境保護(hù)等問(wèn)題中。據(jù)統(tǒng)計(jì),50%數(shù)學(xué)建模問(wèn)題與運(yùn)籌學(xué)內(nèi)容相關(guān),可以用運(yùn)籌學(xué)的方法解決。另外,為各大高校數(shù)次爭(zhēng)得榮譽(yù)的建模隊(duì)伍,長(zhǎng)期以來(lái)一直接受運(yùn)籌學(xué)相關(guān)知識(shí)的培訓(xùn)。
運(yùn)籌學(xué)中最主要的分支是線性規(guī)劃。線性規(guī)劃模型是前蘇聯(lián)著名經(jīng)濟(jì)學(xué)家康托羅維奇于1939年提出的,這一重大發(fā)現(xiàn)使他獲得了諾貝爾經(jīng)濟(jì)學(xué)獎(jiǎng)。1947年G.B.Dantzig提出求解線性規(guī)劃的單純形法。針對(duì)退化問(wèn)題,1952年A.Charner和W.W.Cooper[2]給出了攝動(dòng)法,1954年G.B.Dantzig,A.Orden和P.Wolfe[3]提出了字典序方法,1976年G.G.Bland[4]提出了Bland法則,這些方法都能避免循環(huán)發(fā)生。線性規(guī)劃理論上已趨于成熟,應(yīng)用也越來(lái)越廣泛。事實(shí)上,運(yùn)籌學(xué)中許多問(wèn)題都可以或需要用線性規(guī)劃模型來(lái)描述或近似地描述,如運(yùn)輸問(wèn)題——求解運(yùn)輸問(wèn)題的表上作業(yè)法本質(zhì)上就是單純形法,并且這種方法充分展示了單純形法的魅力。求最短路、最小費(fèi)用最大流的問(wèn)題都可以用線性規(guī)劃模型來(lái)解決。求解指派問(wèn)題的匈牙利法本質(zhì)上也是單純形法[5]。矩陣對(duì)策問(wèn)題最后轉(zhuǎn)化成求解線性規(guī)劃。學(xué)習(xí)運(yùn)籌學(xué)的先修課程主要有線性代數(shù)、微積分、概率論與數(shù)理統(tǒng)計(jì)。事實(shí)上,運(yùn)籌學(xué)不僅應(yīng)用了這些學(xué)科,也從理論上進(jìn)一步發(fā)展了這些學(xué)科。
單純形法是建立在一系列理論基礎(chǔ)之上的。首先,如果線性規(guī)劃的可行域非空,則它是一個(gè)凸集,這個(gè)結(jié)論很容易證明。線性規(guī)劃的可行域的頂點(diǎn)與基可行解之間是一一對(duì)應(yīng)的,所以其頂點(diǎn)個(gè)數(shù)有限,這個(gè)結(jié)論與單純形法的關(guān)系不大,其證明可以省略。其次,線性規(guī)劃若有可行解,則一定有基可行解,這個(gè)結(jié)論是很重要的,為了更好地理解它的證明,我們先看下面的例子。
進(jìn)一步講,若線性規(guī)劃有最優(yōu)解,其最優(yōu)解一定可以在其可行域的頂點(diǎn)上找到,也就是在其基可行解中找到,這樣就把一個(gè)從無(wú)限個(gè)可行解中找最優(yōu)轉(zhuǎn)化成在有限個(gè)可行解中找最優(yōu)。這是單純形法的理論基礎(chǔ)。為了更好地理解這一重要結(jié)論的證明,我們看下一個(gè)例子。
X2的正分量的個(gè)數(shù)是2。由于P2,P4線性無(wú)關(guān),所以X2是基可行解。這樣我們就找到了一個(gè)最優(yōu)解也是基可行解。一般地,若X2的正分量對(duì)應(yīng)的系數(shù)列與線性相關(guān),繼續(xù)上述過(guò)程,直到找到基可行解為止。
從基可行解中找最優(yōu)解所用的方法是單純形迭代法。那么,如何判斷一個(gè)線性規(guī)劃是否有最優(yōu)解?如何判斷一個(gè)基可行解是否是最優(yōu)解?在一個(gè)基可行解不是最優(yōu)的情況下如何迭代到下一個(gè)與其相鄰的更好的基可行解?為回答這些問(wèn)題,我們舉例說(shuō)明。
先講特例再引入最優(yōu)性判別定理、基可行解的改進(jìn)定理以及單純形法的迭代步驟,學(xué)生就容易理解。即使針對(duì)有些專業(yè)的學(xué)生講解這些定理的證明,也容易接受。
總之,現(xiàn)代社會(huì)信息量大,大學(xué)生需要學(xué)習(xí)的課程很多,用于預(yù)習(xí)或復(fù)習(xí)的時(shí)間就很少,這樣上課時(shí)間就尤為珍貴,教師應(yīng)該如何講,才能使學(xué)生當(dāng)堂聽明白所授內(nèi)容,這是一個(gè)必須思考的問(wèn)題。其實(shí),運(yùn)籌學(xué)這門學(xué)科更側(cè)重的是應(yīng)用,數(shù)學(xué)理論并不難,之所以有人覺(jué)得難學(xué),是因?yàn)闆](méi)有把握一種好的學(xué)習(xí)方法。本文針對(duì)單純形法給出了一種循序漸進(jìn)的教學(xué)模式,實(shí)踐證明這種模式能使學(xué)生更容易的理解課堂內(nèi)容,有利于激發(fā)學(xué)生的自信心和學(xué)習(xí)興趣,使學(xué)生在輕松掌握數(shù)學(xué)理論的基礎(chǔ)上,能更好地探討運(yùn)籌學(xué)的經(jīng)典案例的建模和求解,加強(qiáng)學(xué)生運(yùn)用所學(xué)知識(shí)解決實(shí)際問(wèn)題的能力和創(chuàng)新能力。
參考文獻(xiàn):
[1]《運(yùn)籌學(xué)》教材編寫組.運(yùn)籌學(xué)[M].北京:清華大學(xué)出版社,2004.
[2]Charnes,A.And Cooper W.W.,The stepping stone method of explaining linear programming calculations in thansportation problems,Management Science,1954,(1):49-69.
[3]Dantzig,G.B.,Orden.A.and Wolfe.P.,Note on linear programming,Pacific J.Math.1955,(5):183-195.
[4]Bland,G.G.,New finite pivoting rules of Simplex method,Math.Of Operations Research,1977,(2):103-107.
[5]Hamdy,A.Taha,Operations Research-An Introduction[M].北京:人民郵電出版社,2007.
基金項(xiàng)目:2014年度江蘇省研究生教育教學(xué)改革研究與實(shí)踐課題,《運(yùn)籌學(xué)》立體化教學(xué)平臺(tái)建設(shè);2014年中國(guó)礦業(yè)大學(xué)精品資源共享課:《運(yùn)籌學(xué)》
作者簡(jiǎn)介:苗連英(1966-),女,中國(guó)礦業(yè)大學(xué)理學(xué)院教授,主要從事運(yùn)籌學(xué)教學(xué)和科研工作。

