基于樣條曲線的壓氣機特性內插算法研究

黨相懿，楊文廣，蔣東翔

基于樣條曲線的壓氣機特性內插算法研究

黨相懿1,2，楊文廣1，蔣東翔1

（1.清華大學熱能工程系，北京100084；2.中航工業航空動力控制系統研究所，江蘇無錫214063）

針對壓氣機特性曲線中未知轉速數據難以精確計算問題，提出了基于樣條曲線的內插算法。在分析壓氣機性能曲線特點基礎上，通過制作壓比/效率-流量、流量-轉速2組輔助線，并使用樣條曲線對其進行擬合，基于擬合結果計算測試轉速下的特性數據，進而完成了對某型壓氣機壓比/效率特性的內插計算。結果表明：基于樣條曲線的內插算法比RBF神經網絡算法準確性更高，并具有良好的工程應用價值。

壓氣機；性能；樣條曲線；內插算法；仿真計算；RBF網絡；燃氣輪機；熱力學模型

0 引言

作為燃氣輪機的3大部件之一，壓氣機的特性對于仿真結果有顯著影響。通過試驗獲取壓氣機特性費用高昂，且難以獲得全部轉速下的數據。因此，根據有限的試驗數據獲得壓氣機的未知特性數據具有重要意義。壓氣機特性具有很強的非線性特征，采用傳統的線性插值方法難以獲得理想的精度，因此許多學者研究壓氣機特性計算的新算法，如神經網絡方法[1-3]、模糊辨識方法[4]、滑動最小二乘法[5]等。神經網絡算法對于已知轉速線的擬合效果很好，理論上可以達到與試驗值無限逼近；但其擬合精度與泛化能力相矛盾，難以在獲得良好擬合精度的同時達到良好的插值效果[6]。模糊辨識方法對于壓氣機特性的擬合精度比神經網絡的稍差，并且能否用于未知轉速數據的插值計算，以及精度如何等問題還需進一步研究。而滑動最小二乘法算法復雜，計算量較大。樣條曲線作為1種非線性方法，其原理簡單，計算速度快，且擬合結果能夠完全保留樣本數據。

本文基于樣條曲線的特點，構造了壓氣機特性圖的輔助線并對其擬合、插值，進而完成特性曲線的計算。

1 壓氣機特性的內插計算

典型的壓氣機特性曲線如圖1所示。它包括壓比特性曲線和效率特性曲線2部分，圖中數據為相對值[7]。壓氣機的特性一般表示為

式中：π為壓氣機壓比；η為壓氣機效率；m˙為壓氣機流量；n為壓氣機轉速。

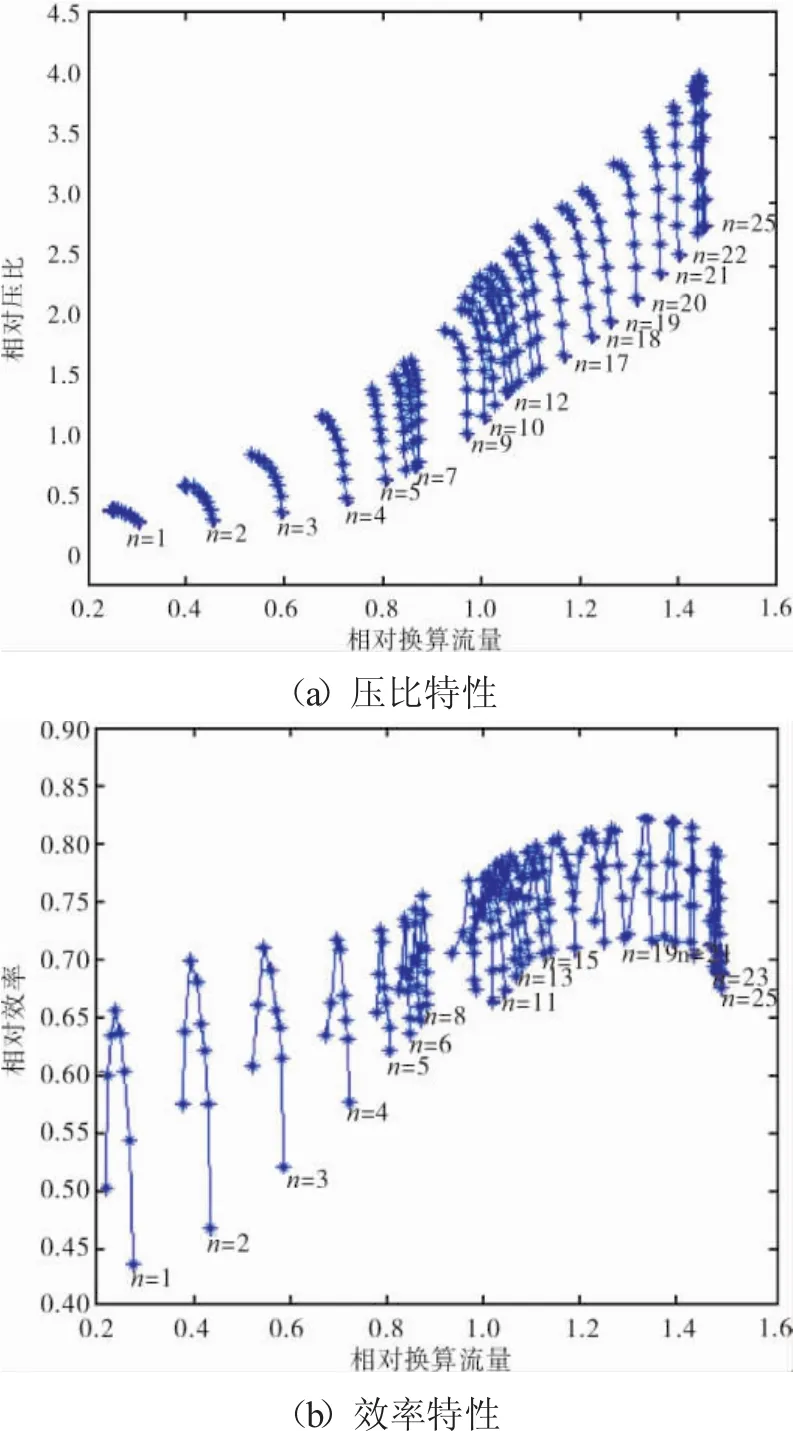
圖1 壓氣機特性曲線

在一般情況下，在壓氣機出廠前會對其進行測試，記錄某些轉速下的壓比、流量和效率等數據。但是這些數據不可能包含所有的轉速，因此在工程中需要根據已有的數據推算未知轉速下壓氣機特性[8]。基于試驗數據的壓氣機特性內插計算是指通過已知等轉速的數據推算未知等轉速線數據，該目標轉速值在已知數據轉速值的范圍內。

從式（1）中可見，特性參數壓比和效率都是雙變量參數，因此需要進行2次插值計算才能確定。在插值變量的選擇上，每個特性參數都有3種方案，即π/η-m˙，m˙-n,π/η-n 的組合。通過分析各類方案的效果，本文選用 π/η-m˙，m˙-n 的插值方式。

基于樣條曲線的壓氣機特性進行計算（圖1），該數據包含25條等轉速線，相對轉速范圍為0.3172～1.1623，分別對應轉速n1-n25。本文選取n4,n10，n18，作為目標內插等轉速線的測試樣本，其他轉速下的數據作為訓練樣本。

2 樣條曲線

樣條曲線是指通過樣本節點來確定的光滑曲線，曲線的形狀由這些點確定，在節點兩邊樣條曲線段光滑。按照控制點處曲線的連續階數，樣條曲線具有不同的階次。比如最常用的3次樣條曲線，在控制點處第2階導數連續，即其曲率連續變化。類似的還有斜率連續的2次樣條曲線以及更高次的樣條曲線。

下面給出3次樣條曲線的嚴格數學定義[9]。

設 1 組數據點 Pi(xi,yi)，i=1,2,3,…,n 且 hi=xi+1-xi＞0,i=2,3,4,…,n。若有y=S(x)滿足以下條件：（1）在 Pi(xi,yi)點上有 y=S(xi)；

（2）S(x)在區間[x1,xn]上2階連續可導；

（3）在每個區間[xi,xi+1]上，S(x)是x不高于3次的多項式。

則S(x)稱為過點Pi(xi,yi),i=1,2,3…,n的3次樣條函數，由該函數構成的曲線稱為3次樣條曲線。3次樣條曲線的求解方法已非常成熟[10]，本文不再贅述。從定義可知，3次樣條曲線擬合數據的本質是通過“分段低次”代替單純地增加擬合多項式的次數，從而更加適合對非線性曲線進行擬合計算。

分別利用5次多項式和3次樣條曲線對同1組數據進行擬合的結果如圖2所示。從圖中可見，3次樣條曲線的擬合效果遠好于多項式的。圖中“spline”特指3次樣條曲線。

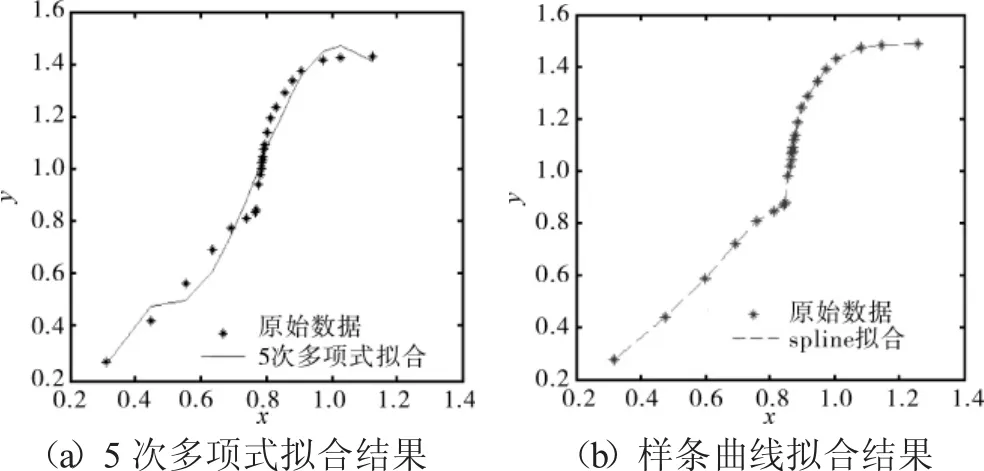
圖2 多項式與樣條曲線擬合效果比較

3 壓氣機特性內插算法

為了對壓氣機特性進行內插計算，本文使用了2組輔助線，具體以壓比特性計算為例進行說明。

（1）構造輔助線

特性曲線有25條等轉速線，每條等轉速線上有8個點，形成1個25×8的點陣A。在壓比特性圖上，依次連接點陣A的每1列就形成8條輔助線，如圖3（a）所示。從圖中可見，每條輔助線都是1條參數為π,m˙的曲線，這就是進行π-m˙參數擬合的對象。

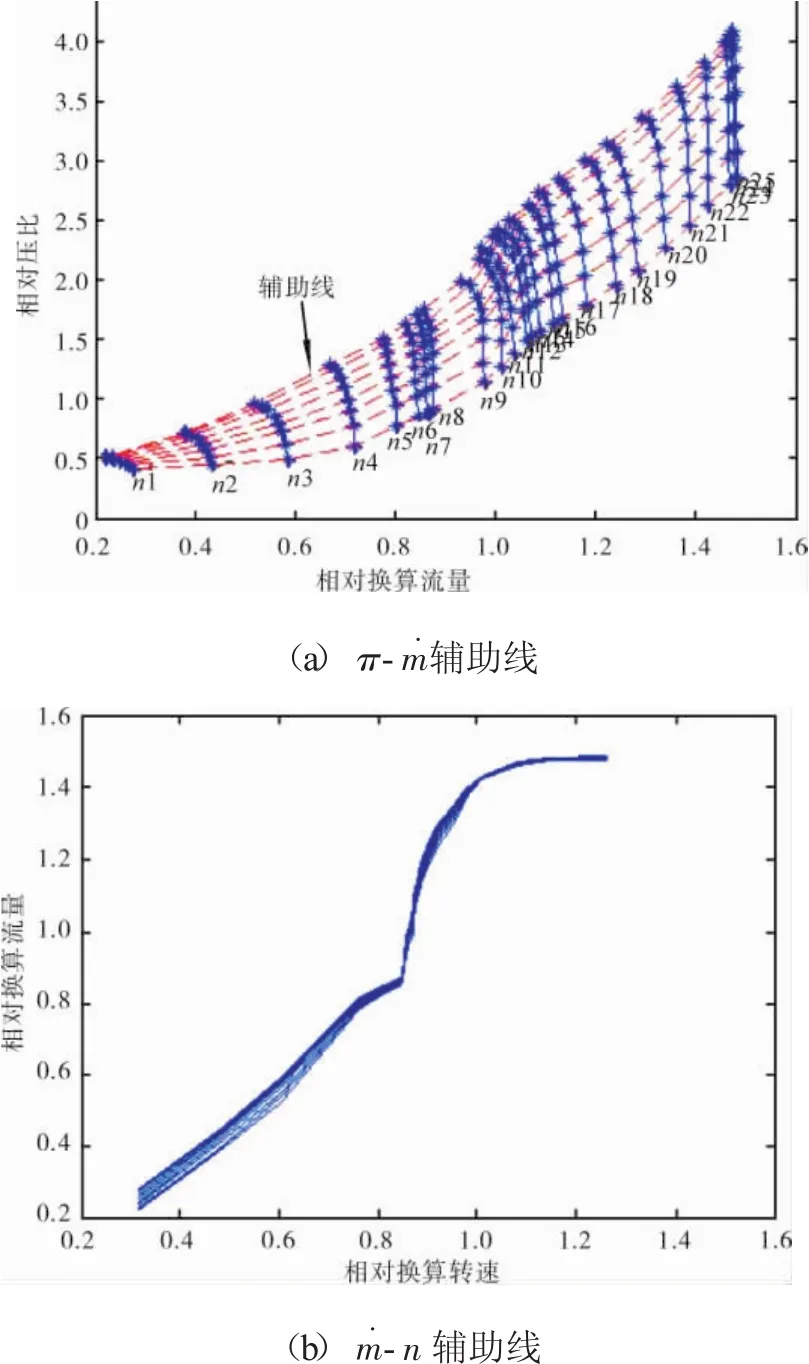
圖3 輔助線

對于m˙-n插值，需要提取各條輔助線上點的流量和轉速數據，重新繪制出需要插值的8條曲線，其結果如圖 3（b）所示。

（2）m˙-n 插值

分別使用RBF網絡和樣條曲線對8條m˙-n輔助線進行擬合，得到8個RBF網絡和8條樣條曲線；將目標轉速n4，n10，n18分別代入訓練好的網絡或樣條曲線，得到該目標等轉速線與輔助線相交8個點的流量值。

（3）π-m˙插值

分別使用RBF網絡和樣條曲線對8條π-m˙輔助線進行擬合，然后將（2）中m˙-n插值所得流量值代入該網絡或樣條曲線中就得到輔助線與該等轉速線相交8個點的壓比值。

（4）做出壓比曲線

根據（2）和（3）獲得的流量與壓比值，在壓比特性曲線圖上可以獲得8個點，這就是內插得到的目標轉速壓比特性曲線。其上、下邊界分別由第1和第8條輔助線界定。

壓氣機效率特性的內插與此類似，只需將（3）中的擬合對象替換成η-m˙輔助線即可。

4 結果和分析

按照第3章所述方法，針對圖1數據中n4,n10,n18 3條等轉速線進行內插計算。RBF網絡和3次樣條曲線的結果分別如圖4、5所示。

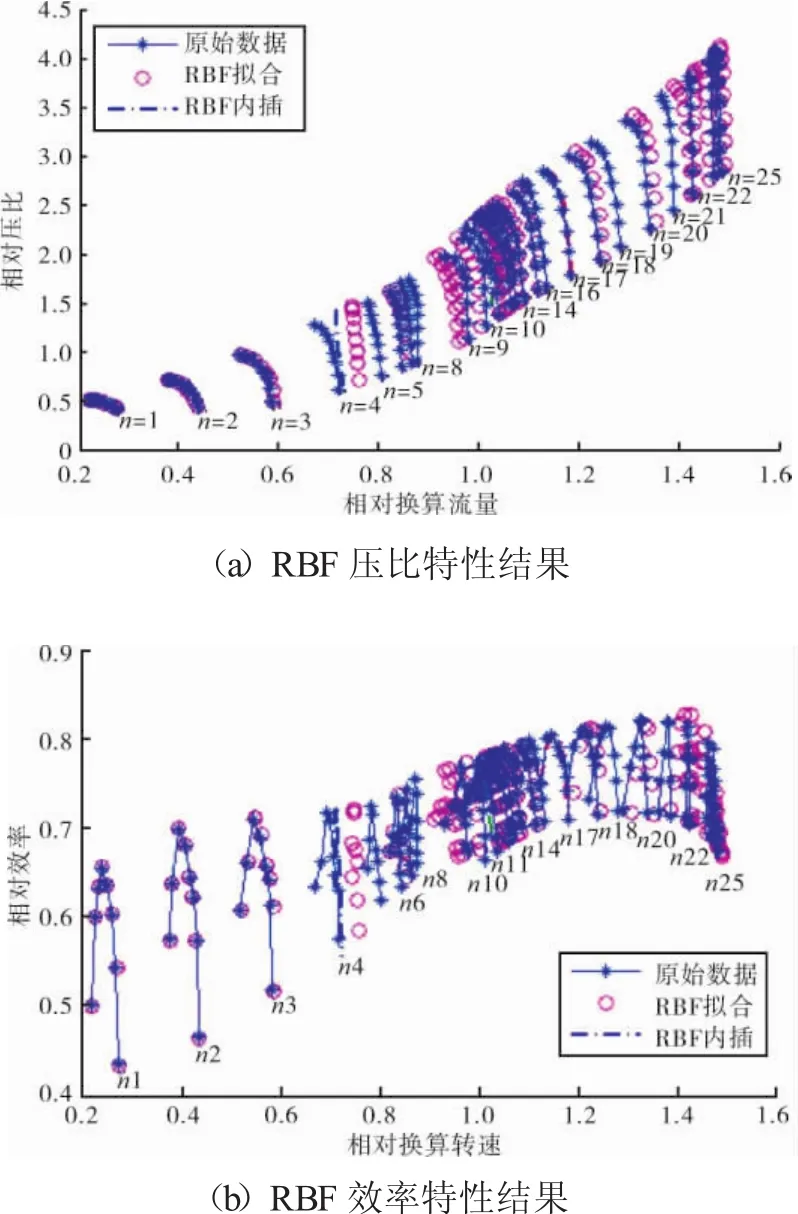
圖4 RBF神經網絡內插結果

3條測試等轉速線內插計算的壓比結果和效率結果分別如圖6、7所示。圖中RBF指RBF神經網絡，spline指3次樣條曲線。圖6中RBF網絡的n18插值結果看似n17的插值結果，這只是由誤差引起的巧合。

圖5 3次樣條曲線內插結果

圖6 等轉速線的壓比插值結果

圖7 等轉速線的效率插值結果

表1 等轉速線壓比特性內插誤差

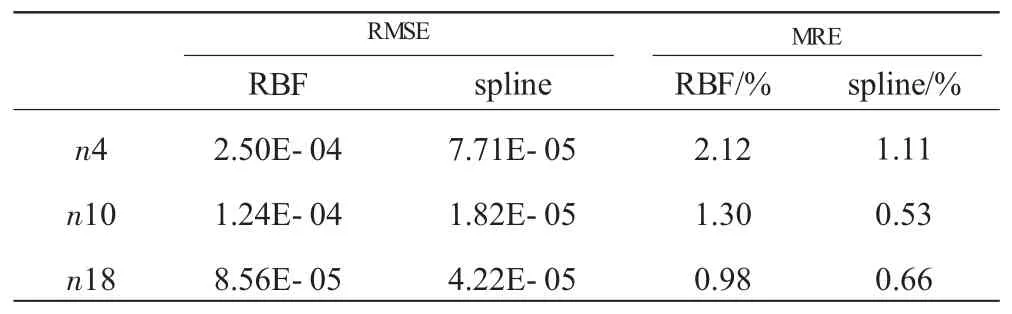
表2 等轉速線效率特性內插誤差

內插結果均方根誤差和平均相對誤差見表1、2。表中RMSE為均方根誤差，MRE為平均相對誤差。

從表中結果可知，3次樣條曲線的內插精度要優于RBF神經網絡的。這是因為RBF網絡要求大量的訓練樣本，且其準確性和泛化性是1對矛盾。對于本例來說，m˙-n輔助線的訓練樣本較少，且曲線形態變化大，因此RBF網絡難以在準確性和泛化性上都獲得滿意的結果，插值誤差較大，傳遞到第2次π/η-m˙插值上使整體插值精度下降。而樣條曲線對于形態變化較大的曲線擬合效果較好，且受樣本數量限制較小，因此具有更好的內插精度。

為了驗證這一結論，使用3次樣條曲線代替RBF網絡對m˙-n 插值，π/η-m˙插值仍使用 RBF 網絡，插值結果的平均相對誤差見表3。表3顯示RBF與樣條曲線結合的插值方式相對單一RBF插值，壓比結果均更好，且轉速越高差別越明顯；效率結果低轉速n4插值精度稍低，中高轉速n10精度相當，n18精度提高。結合圖3可知，因為中低轉速區m˙-n基本呈線性變化，樣條曲線的擬合優勢并未顯現。

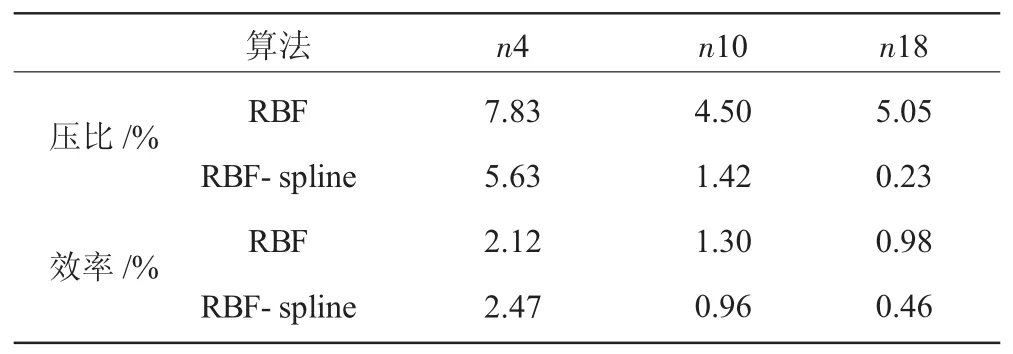
表3 RBF-樣條曲線結合方法的平均相對誤差

5 結論

（1）基于某型發動機特性數據，構造了 π/η-m˙，m˙-n輔助線，并分別使用RBF神經網絡和3次樣條曲線插值計算，獲得了測試等轉速線下的特性曲線。

（2）3次樣條曲線內插效果優于RBF神經網絡的，其優勢在于對m˙-n輔助線的計算。

（3）基于3次樣條曲線內插計算壓氣機特性可以獲得較高的精度，對提高燃氣輪機仿真精度具有重要意義。

[1]梁磊,徐洪志,安學利,等.航空發動機故障特征仿真研究[J].計算機仿真，2012（4）：15.LIANG Lei，XU Hongzhi，AN Xueli,et al.Faults analysis and simulation for aeroengine[J].Computer Simulation，2012（4）：015.(in Chinese)

[2]趙雄飛，劉永葆，賀星，等.基于統計學檢驗指標的燃氣輪機部件特性方程擬合次數的選擇[J].航空發動機，2011，37（5）：7-10.ZHAO Xiongfei，LIU Yongbao，HE Xing，et al.Selection of fitting order times of gas turbine component characteristic equation based on statistics evaluation indexes[J].Aeroengine，2011，37（5）：7-10.(in Chinese)

[3]劉小方,蔣磊,司品順,等.燃氣輪機壓氣機特性曲線的擬合方法[J].艦船科學技術，2012 34（7）:61-63.LIU Xiaofang，JIANGLei，SIPinshun，et al.Research on curve fitting method of compressor characteristic curve[J].Ship Science and Technology，2012，34（7）：61-63.(in Chinese)

[4]王志濤，李淑英，譚智勇.基于BP和RBF神經網絡壓氣機特性曲線擬合方法的研究[J].汽輪機技術，2009，51（2）：94-99.WANG Zhitao,LI Shuying,TAN Zhiyong.Comparing study on the fitting method of compressor characteristic curve based on BP and RBF neural network[J].Turbine Technology,2009，51（2）：94-99.(in Chinese)

[5]彭靖波,謝壽生.基于RBF神經網絡的壓氣機特性仿真[J].推進技術，2006，27（1）：30-32.PENG Jingbo,XIE Shousheng.Compressor characteristic simulation based on RBF neural network[J].Journal of Propulsion Technology，2006，27（1）：30-32.(in Chinese)

[6]Ghorbanian K,Gholamrezaei M.An artificial neural network approach to compressor performance prediction[J].Applied Energy，2009，86（7）:1210-1221.

[7]蔣愛武，謝壽生.基于支持向量機和粒子群算法的壓氣機特性計算[J].航空動力學報，2010（11）：2571-2577.JIANG Aiwu,XIE Shousheng.Method to achieving compressor characteristics based on support vector machine(SVM)and particle swarm optimization(PSO)[J].Journal of Aerospace Power，2010（11）：2571-2577.(in Chinese)

[8]唐麗麗，王廣軍.壓氣機特性的模糊辨識[J].計算機仿真，2009，26（1）：70.TANG Lili，WANG Guangjun.Fuzzy identification of air compressor characteristics[J].Computer Simulation，2009，26（1）：70.(in Chinese)

[9]楊欣毅，沈偉，劉海峰，等.一種應用滑動最小二乘求取壓氣機特性的方法[J].航空動力學報，2009，24（8）:1741-1746.YANG Xinyi,SHEN Wei,LIU Haifeng,et al.Compressor characteristics generation method using moving least square[J].Journal of Aerospace Power，2009，24（8）:1741-1746.(in Chinese)

[10]李祚泳，易勇鷙.BP網絡學習能力與泛化能力之間的定量關系式[J].電子學報，2003，31（9）：1341-1344.LI Zuoyong，YI Yongzhi.Quantitative relation between learning ability and generalization ability of BP neural network[J].Acta Electronica Sinica，2003，31（9）：1341-1344.(in Chinese)

[11]郭云，吳松強.三次樣條曲線擬合的算法及實現[J].計算機應用研究，1996，13（6）：41-42.GUO Yun，WU Songqiang.Algorithm and realization of cubic spline curve fitting[J].，1996，13（6）：41-42.(in Chinese)

[12]駱廣琦，桑增產，王如根，等.航空燃氣渦輪發動機數值仿真[M].北京：國防工業出版社，2007：182-183.LUO Guangqi，SANG Zengchan，WANG Rugen，et al.Numerical methods for aviation gas turbine engine simulation [M].Beijing：National Defense Industry Press，2007：182-183.(in Chinese)

[13]Kong C，Ki J.Components map generation of gas turbine engine using genetic algorithms and engine performance deck data[J].Journal of Engineering for Gas Turbines and Power，2007，129（2）：312-317.

[14]柏慶昆.一般的三次參數樣條曲線的幾何連續性及其插值方法[D].長春：東北師范大學，2006.BAI Qingkun.The geometry continuity and interpolation method of general cubic parametric spline curves[D].Changchun：Northeast Normal University，2006.(in Chinese)

[15]陳文略，王子羊.三次樣條插值在工程擬合中的應用[J].華中師范大學學報：自然科學版，2004，38（4）：418-422.CHEN Wenlve，WANG Ziyang.The application of cubic splines interpolation in the project fitting[J].Journal of Central China Normal University ：Natural Sciences，2004，38（4）：418-422.(in Chinese)

Interpolation Algorithm of Compressor Characteristics Based on Spline

DANG Xiang-yi,YANG Wen-guang,JIANG Dong-xiang
（1.Department of Thermal Engineering,Tsinghua University,Beijing 100084,China,2.AVIC Aeroengine Control Institute,Wuxi Jiangsu 214063,China）

Consideringtheunknownrotatingspeed dataof compressor characteristicswerenoteasy tocalculateaccurately,ainterpolation algorithmbased on splinewas presented.The splinecurveswereused to fit the auxiliary lines of compression ratio/efficiency to massflow and massflow to rotating speed based on analysis of the compressor characteristics.Thecharacteristicsdata were calculated at test speed based on the spline-fitting results.The interpolation algorithm of pressure ratio/efficiency characteristics of a compressor were completed.The results showthatthealgorithmismoreaccurate,and hasbetter engineeringapplication valuethan an algorithmbased on RBFnetwork.

compressor;performance;spline;interpolation algorithm;simulation calculation;RBF network;gas turbine;thermodynamic model

V235.11+3

A

10.13477/j.cnki.aeroengine.2015.01.004

2014-03-13 基金項目：國家自然科學基金（60979014）資助

黨相懿（1990），男，在讀碩士研究生，研究方向為燃氣輪機/航空發動機故障診斷；E-mail：dangxiangyi110@sina.com。

黨相懿，楊文廣，蔣東翔.基于樣條曲線的壓氣機特性內插算法研究[J].航空發動機，2015，41（1）：22-26.DANGXiangyi,YANGWenguang,JIANGDongxiang.Interpolation algorithmof compressor characteristicsbased on spline[J].Aeroengine，2015，41(1)：22-26.

（編輯：沈廣祥）