基于改進(jìn)CS算法的整像素數(shù)字散斑相關(guān)方法

周海芳，楊秋翔，楊 劍

（中北大學(xué) 計算機(jī)與控制工程學(xué)院，山西 太原030051）

0 引 言

數(shù)字散斑相關(guān)方法 （digital speckle correlation method，DSCM）研究的核心內(nèi)容是相關(guān)搜索方法［1］，早期的相關(guān)搜索方法主要有兩種類型［2］：一種是將位移和位移導(dǎo)數(shù)同時搜索，如粗－細(xì)相關(guān)法；另一種是認(rèn)為位移導(dǎo)數(shù)值對相關(guān)系數(shù)的貢獻(xiàn)遠(yuǎn)小于位移值，為了節(jié)省時間只進(jìn)行位移搜索，如十字搜索法。為了提高搜索的速度，將相關(guān)搜索用數(shù)學(xué)手段轉(zhuǎn)化為迭代格式求解，如Newton－Rapson 迭代算法，但迭代算法嚴(yán)重依賴初值的選取。若將上述相關(guān)搜索方法用于多峰值搜索就很容易陷入局部最優(yōu)，從而導(dǎo)致搜索結(jié)果不準(zhǔn)確，為此一些學(xué)者將新的數(shù)學(xué)理論 （如頻域傅里葉方法、神經(jīng)網(wǎng)絡(luò)方法、小波變換方法等）引入到DSCM 方法中，給相關(guān)搜索帶來了新的途徑，不僅使得搜索精度有了數(shù)量級的提高，而且算法更加智能化。

布谷鳥搜索 （cuckoo search，CS）算法［3，4］是一種新穎的群體智能優(yōu)化算法，其優(yōu)勢主要是模擬鳥類及果蠅特殊的Lévy飛行模式進(jìn)行搜索，算法簡單、參數(shù)少，易于實現(xiàn)。然而CS算法是一種新興的仿生算法，其收斂速度和求精能力仍需要進(jìn)一步改善。Valian等研究了步長因子對算法性能的影響，采用動態(tài)調(diào)整的策略增加了算法的性能［5］；鄭洪清等給出了基于最佳鳥巢位置的自適應(yīng)調(diào)整步長的策略［6］；王凡等提出將高斯分布引入CS算法［7］。本文通過引入非均勻變異算子和最優(yōu)鳥巢擾動策略對CS算法進(jìn)行改進(jìn)，并用4個標(biāo)準(zhǔn)測試函數(shù)進(jìn)行驗證，最后將改進(jìn)后的CS算法應(yīng)用到了數(shù)字散斑相關(guān)方法中。

1 數(shù)字散斑相關(guān)方法基本原理

數(shù)字散斑相關(guān)方法基本原理請參見文獻(xiàn) ［8］。相關(guān)系數(shù)公式是目標(biāo)子區(qū)與樣本子區(qū)相互關(guān)系的定量描述，表示匹配時的相似程度［8］。相關(guān)系數(shù)公式有很多種，本文采用以下公式

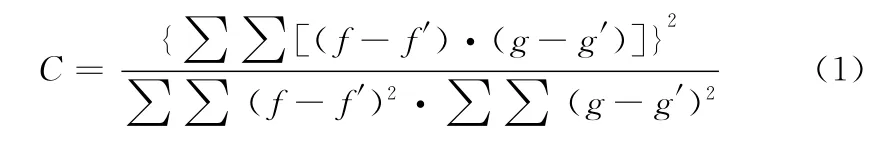
式中：C—— 相關(guān)系數(shù)，C 越大表示越相關(guān)，C ＝1時完全相關(guān)。f＝f（i，j）、g＝g（i＋u，j＋v）表示分別為以源點和目標(biāo)點為中心的散斑圖的灰度值函數(shù)；f′、g′分別為所在標(biāo)記區(qū)域的平均灰度。

2 基本的CS算法

布谷鳥搜索算法是模擬自然界中布谷鳥種群寄生繁衍的生物行為而衍生出的搜索算法，同時結(jié)合了鳥類及果蠅特殊的Lévy飛行模式，全局搜索能力很強(qiáng)，適合用于多目標(biāo)優(yōu)化問題求解。該算法的構(gòu)建基于3個理想規(guī)則，具體規(guī)則請參見文獻(xiàn) ［4］。在3個理想規(guī)則的基礎(chǔ)上，布谷鳥按Lévy飛行模式搜索鳥巢的路徑和位置更新公式如下

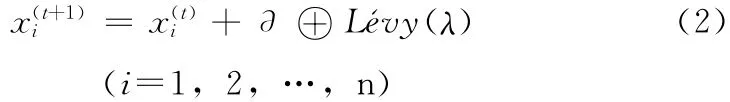
式中：x（t）i——第t代的第i 個鳥巢位置；——點對點乘法；——步長信息；Lévy（λ）——隨機(jī)搜索路徑。

在按一定的發(fā)現(xiàn)概率Pa丟棄部分鳥巢之后采用隨機(jī)游動重新生成相同數(shù)量的新鳥巢，位置更新公式如下

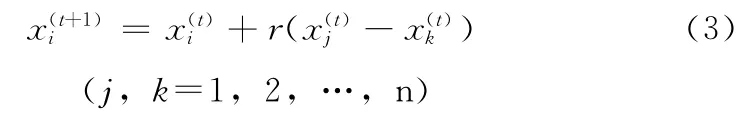
式中：r 是 （0，1）區(qū)間均勻分布的隨機(jī)數(shù)，x（t）j、x（t）k是第t代的兩個隨機(jī)鳥巢位置。

3 改進(jìn)后的CS算法 （ICS算法）

3.1 非均勻變異算子

布谷鳥每次尋巢過程中的隨機(jī)搜索路徑即Lévy（λ）的長度和方向都是髙度隨機(jī)改變的，具有非常大的盲目性。雖然算法在迭代初期很利于全局搜索，但在迭代后期就很容易跳過最優(yōu)解，出現(xiàn)震蕩現(xiàn)象，造成算法收斂速度和尋優(yōu)精度大大降低。本文引入非均勻變異算子［9］，自適應(yīng)調(diào)節(jié)步長使得算法在迭代前期可以在整個定義域中大范圍搜索，盡可能發(fā)現(xiàn)潛在的區(qū)域，隨著迭代的進(jìn)行，步長逐漸減小，到迭代臨近結(jié)束時，步長趨于零，此時布谷鳥可以在當(dāng)前最優(yōu)鳥巢位置的狹小鄰域中精細(xì)搜索，從而準(zhǔn)確定位最優(yōu)鳥巢位置。

假 設(shè) 第t 代 的 第i 個 鳥 巢 的 位 置 為xi（t）＝｛xi（1t），xi（2t），…，xi（dt）｝T，對鳥 巢的第j維 位 置 執(zhí) 行 變 異，則 變異后的分量為

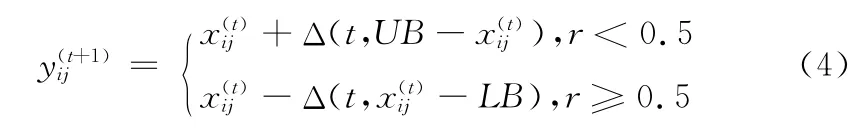
在Δ（t，y）＝y(tǒng)·（1－y（1－Tt）b）中，t是當(dāng)前迭代次數(shù)，T是最大迭代次數(shù)，r 是服從 （0，1）區(qū)間均勻分布的隨機(jī)數(shù)，b為決定變異非均勻度的系統(tǒng)參數(shù)，［LB，UB］為搜索空 間 的 范 圍， 則 更 新 后 的 鳥 巢 位 置 為 yi（t＋1）＝｛yi（1t＋1），yi（2t＋1），…，yi（dt＋1）｝T。

3.2 鳥巢位置更新策略

在標(biāo)準(zhǔn)CS算法中，各個布谷鳥都是按照自己的方式盲目飛行，相互之間并沒有進(jìn)行交流，這并沒有充分顯示出智能算法的優(yōu)點。本文借鑒粒子群算法的飛行速度和位置更新機(jī)制，令通過隨機(jī)游動得到的新鳥巢位置由兩部分組成，其中一部分信息繼承于自身的位置，另一部分吸收于上一代的最優(yōu)鳥巢位置信息，從而加快整個算法的收斂速度。具體公式如下

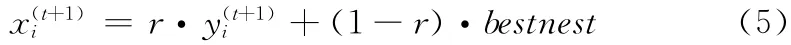
式中：r是（0，1）區(qū)間均勻分布的隨機(jī)數(shù)，y（t＋1）i是通過非均勻變異因子更新得到的鳥巢位置，bestnest是第t代的最優(yōu)鳥巢位置。

3.3 最優(yōu)鳥巢擾動策略

在鳥巢主人發(fā)現(xiàn)外來布谷鳥蛋步驟后，不是直接進(jìn)入下一次迭代而是引入最優(yōu)鳥巢擾動策略。在多維函數(shù)的尋優(yōu)過程中，對不同維數(shù)采用相同范圍的擾動顯然不能滿足求解需求，本文將最優(yōu)鳥巢位置依據(jù)方差可調(diào)的正態(tài)隨機(jī)分布進(jìn)行逐維擾動，該變異操作不但能有效避免CS算法陷入局部最優(yōu)，而且可以增加整個種群的多樣性

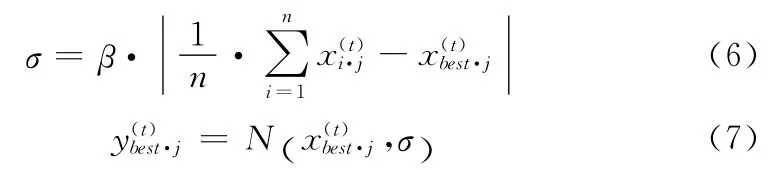
3.4 ICS算法的基本步驟

步驟1 初始化參數(shù)：將不同的求解問題按照相應(yīng)的要求初始化鳥巢個數(shù)n，解空間維數(shù)d，最大迭代次數(shù)T，搜索空間范圍 ［LB，UB］，發(fā)現(xiàn)概率Pa，適應(yīng)度函數(shù)fit（x）。

步驟2 初始化種群：在 ［LB，UB］空間范圍內(nèi)隨機(jī)生成n個鳥巢，令t＝1，其中第i個鳥巢的位置為xi（1）＝｛xi（11），xi（21）…，xij（1）…xi（d1）｝T，計 算 各 個 鳥 巢 的 適 應(yīng) 度 函 數(shù)值，求出最優(yōu)鳥巢bestnest。

步驟3 鳥巢位置進(jìn)行隨機(jī)游動操作：將每個鳥巢按式（4）方式隨機(jī)游走，式 （5）確定鳥巢按游走方式得到的最終位置并計算適應(yīng)度函數(shù)值，與更新前的比較后保留較優(yōu)鳥巢位置。

步驟4 鳥巢主人發(fā)現(xiàn)外來鳥蛋操作：產(chǎn)生服從 ［0，1］均勻分布的隨機(jī)數(shù)r，若r ＞Pa，則按式 （3）更新鳥巢位置并計算適應(yīng)度函數(shù)值，與更新前的比較后保留較優(yōu)鳥巢位置同時更新bestnest。

步驟5 最優(yōu)鳥巢擾動操作：將bestnest按式 （6）、式（7）進(jìn)行擾動得到更新后的鳥巢并計算適應(yīng)度函數(shù)值，與更新前的比較后保留較優(yōu)鳥巢為bestnest。

步驟6 判斷操作：若fit（bestnest）沒有達(dá)到要求且t＜T，則令t＝t＋1，跳轉(zhuǎn)到步驟3，否則循環(huán)結(jié)束，輸出最優(yōu)鳥巢位置及適應(yīng)度函數(shù)值。

4 仿真實驗

4.1 實驗設(shè)計

本文通過尋找4個標(biāo)準(zhǔn)測試函數(shù)的最小值0為例，進(jìn)行仿真實驗來評估ICS算法的性能，標(biāo)準(zhǔn)測試函數(shù)及其相關(guān)參數(shù)設(shè)置見表1，測試平臺為Matlab2013a、windows7，處理器CPUM370，主頻2.4GHz，內(nèi)存2G。

表1 測試函數(shù)及其參數(shù)設(shè)置

實驗中種群規(guī)模n＝100，T＝500。為克服算法的偶然誤差，對各測試函數(shù)獨立運行50 次，取其最優(yōu)值、最差值、平均值和標(biāo)準(zhǔn)偏差與基本CS算法進(jìn)行比較。

4.2 實驗結(jié)果分析

表2描述了標(biāo)準(zhǔn)CS和ICS算法對以上4個測試函數(shù)的測試結(jié)果，對于低維函數(shù)Schaffe和Rosenbrock，ICS比CS算法的平均搜索精度分別提高4和9個數(shù)量級，最優(yōu)值分別提高8個數(shù)量級，ICS的最差值比CS算法的最優(yōu)值還要分別提高3和5個數(shù)量級。在高維函數(shù)Sphere中，ICS比CS算法的平均搜索精度提高7個數(shù)量級，且成功找到最優(yōu)值，最差值要比CS算法的最優(yōu)值還要提高6個數(shù)量級。在高維函數(shù)Rastigrin中，ICS比CS算法的平均搜索精度提高1個數(shù)量級，最優(yōu)值提高7個數(shù)量級。縱觀整個數(shù)據(jù)表，無論是解的質(zhì)量上 （最優(yōu)值、平均值和最差值），還是算法穩(wěn)定性方面 （標(biāo)準(zhǔn)偏差），ICS算法都要優(yōu)于CS算法。

從圖1 （a）～ （d）的ICS和CS算法的收斂曲線可以看出，ICS算法的收斂速度有明顯提高且迭代次數(shù)遠(yuǎn)小于CS算法。

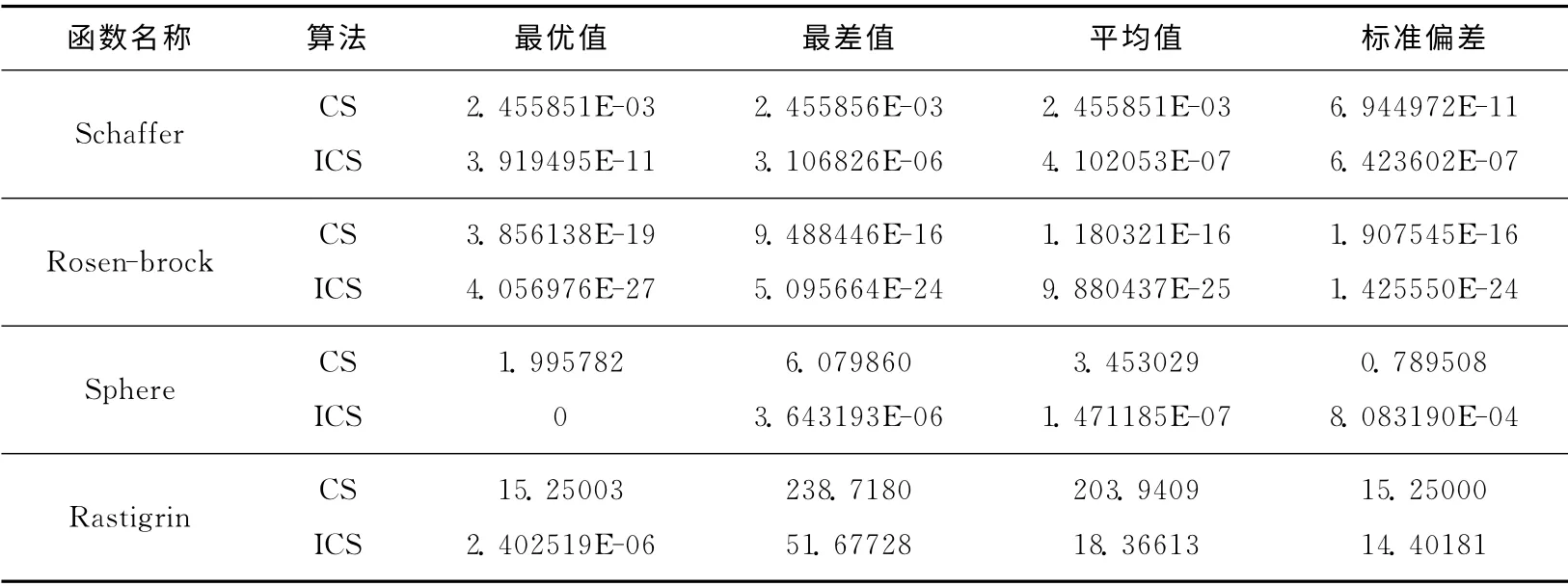
表2 兩種優(yōu)化算法的計算結(jié)果

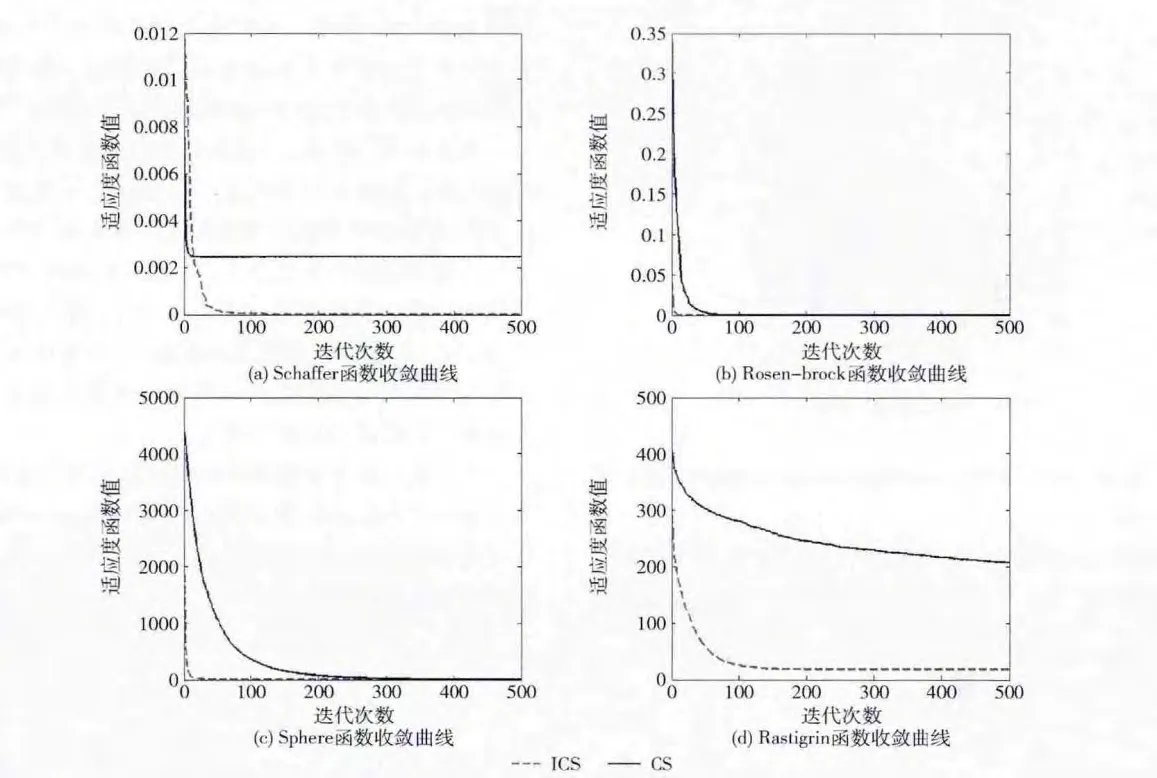
圖1 相關(guān)測試函數(shù)收斂曲線

5 ICS算法在數(shù)字散斑相關(guān)方法中的應(yīng)用

5.1 ICS算法測量散斑圖像位移的流程

基于以上討論，用改進(jìn)的布谷鳥搜索算法對散斑圖平移后的位移進(jìn)行整像素的相關(guān)搜索，流程如圖2所示。

圖2 ICS算法流程

5.2 ICS算法測量模擬散斑圖位移

先制作模擬散斑圖，圖3（a）為源圖片，將源圖片向右平移17個像素，向下5個像素，得到移動后的圖片圖3（b）。

圖3 模擬散斑

以模擬散斑圖為研究對象，取移動前某一點的位移進(jìn)行相關(guān)搜索。以該點為中心選取邊長為21像素的正方形區(qū)域作為樣本子區(qū)［10］，在移動后的圖片上以相同的點為中心取邊長為80像素的正方形區(qū)域作為搜索區(qū)域，相關(guān)系數(shù)C在搜索區(qū)域內(nèi)的分布如圖4所示。可以發(fā)現(xiàn)，圖4的中央有一個最高峰，在最高峰附近還有多個較高的局部峰。

ICS算法測量模擬散斑圖位移時初始參數(shù)設(shè)置為：Tmax為30，鳥巢個數(shù)為15，樣本子區(qū)為21×21 像素，搜索區(qū)域為80×80像素，Pa.max＝0.95，Pa.min＝0.15。

圖5 （a）～ （c）分別給出了迭代次數(shù)N＝1、5、15時各個鳥巢在相關(guān)系數(shù)水平等勢線上所處的位置。可以發(fā)現(xiàn)，第1代鳥巢的分布是雜亂無章的，而第5代鳥巢整體上向最優(yōu)解靠攏，在第15代時絕大數(shù)鳥巢與最優(yōu)解重合。

圖4 相關(guān)系數(shù)分布

5.3 ICS算法與CS、PSO （particle swarm optimization）算法比較

用3種算法測量相同的散斑圖位移，固定迭代次數(shù)為30，種群個數(shù)為15，樣本子區(qū)尺寸為21×21像素，搜索域尺寸為60×60像素，各算法分別進(jìn)行100次的獨立實驗，表3列出了適應(yīng)度C 的最差值，最優(yōu)值，平均值，尋優(yōu)成功率和各算法獨立運行一次所用的平均時間。

從表3可以看出，3種算法在100次獨立試驗中都找到過最優(yōu)值，但綜合C 最差值、平均值、尋優(yōu)成功率可以看出PSO 算法最容易陷入局部最優(yōu)，并且在100次獨立實驗中陷入局部最優(yōu)的次數(shù)最多；ICS算法相對PSO、CS算法尋優(yōu)成功率分別提高29.3%、18.3%，平均誤差分別降低了294%、85.8%。說明ICS算法與CS算法在計算時間相差不大的情況下?lián)碛懈鼜?qiáng)的跳出局部最優(yōu)的能力，搜索精度更高，尋優(yōu)成功的概率更大。

為了進(jìn)一步分析各算法在測量散斑圖位移的收斂性能，圖6給出了各算法在測量散斑圖位移時的迭代過程。圖中標(biāo)記點的適應(yīng)度函數(shù)值都是取在100次獨立實驗中迭代次數(shù)對應(yīng)的適應(yīng)度平均值。

圖5 鳥巢運動軌跡

表3 各算法的計算結(jié)果

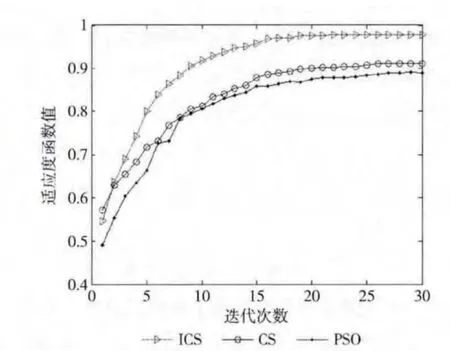
圖6 各算法迭代過程

從圖6可以看出：在迭代初期，ICS算法全局尋優(yōu)能力最強(qiáng)，在鎖定最優(yōu)值范圍后，局部收斂能力最強(qiáng)并且求精能力最優(yōu)。而CS算法在收斂速度和求精能力上都比粒子群算法略優(yōu)。

6 結(jié)束語

針對基于傳統(tǒng)DSCM 的計算結(jié)果容易陷入局部最優(yōu)，求解精度不高，后期收斂速度慢等缺點，本文將基于群體智能的CS算法引入到DSCM 中，并對基本的CS算法進(jìn)行了改進(jìn)，將ICS，CS，PSO 這3種算法用于測量預(yù)制模擬散斑圖平移后的整像素位移，實驗結(jié)果表明CS 算法在DSCM 中是有效的，并且ICS 方法較CS，PSO 算法在DSCM 中跳出局部最優(yōu)的能力最強(qiáng)，收斂速度最快和尋優(yōu)精度最高。

［1］YANG Yuhang.Study of digital speckle correlation method［D］.Jilin：Changchun University of Science and Technology，2014：5－23 （in Chinese）. ［楊宇航.數(shù)字散斑相關(guān)方法的研究 ［D］.吉林：長春理工大學(xué)，2014：5－23.］

［2］LIANG Heng.Research on measurement techniques based on digital speckle correlation method ［D］.Anhui：Hefei University of Technology，2014：10－30 （in Chinese）. ［梁恒.基于數(shù)字散斑相關(guān)方法的測量技術(shù)研究 ［D］.安徽：合肥工業(yè)大學(xué)，2014：10－30.］

［3］LONG Wen，CHEN Le.Hybrid cuckoo search algorithm for solving constrained chemical engineering optimization problems［J］.Journal of Computer Applications，2014，34 （2）：523－527 （in Chinese）.［龍文，陳樂.求解約束化工優(yōu)化問題的混合布 谷 鳥 搜 索 算 法 ［J］.計 算 機(jī) 應(yīng) 用，2014，34 （2）：523－527.］

［4］Gandomt A，Yang X，Alavi A.Cuckoo search algorithm：Ameta－h(huán)euristic approach to solve structural optimization problems ［J］.Engineering with Computer，2013，29 （1）：17－35.

［5］Valian E，Mohanna S，Tavakoli S.Improved cuckoo search algorithm for global optimization ［J］.Int J Communications and Information Technology，2011，1 （1）：31－44.

［6］ZHENG Hongqing，ZHOU Yongquan.Self－adaptive step cuckoo search algorithm ［J］.Computer Engineering and Applications，2013，49 （10）：68－71 （in Chinese）. ［鄭 洪 清，周永權(quán).一種自適應(yīng)步長布谷鳥搜索算法 ［J］.計算機(jī)工程與應(yīng)用，2013，49 （10）：68－71.］

［7］WANG Fan，HE Xingshi，WANG Yan.The cuckoo search algorithm based on Gaussian disturbance［J］.Journal of Xi’an Polytechnic University，2011，25 （4）：566－569 （in Chinese）.［王凡，賀興時，王燕.基于高斯擾動的布谷鳥搜索算法 ［J］.西安工程大學(xué)學(xué)報，2011，25 （4）：566－569.］

［8］CHEN Zhixin，LIANG Jin，GUO Cheng.Application of digital speckle correlation method to deformation measurement［J］.Optics and Precision Engineering，2011，19 （7）：1480－1485 （in Chinese）.［陳志新，梁晉，郭成.數(shù)字散斑相關(guān)法在變形測量中的應(yīng)用 ［J］.光學(xué)精密工程，2011，19 （7）：1480－1485.］

［9］ZHAO Xinchao，LIU Guoli，LIU Huqiu，et al.Particle swarm optimization algorithm base on non－uniform mutation and multiple stages perturbation ［J］.Chinese Journal of Computers，2014，37 （9）：2058－2070 （in Chinese）. ［趙新超，劉國蒞，劉虎球，等.基于非均勻變異和多階段擾動的粒子群優(yōu)化算法 ［J］.計算機(jī)學(xué)報，2014，37 （9）：2058－2070.］

［10］DU Yazhi，WANG Xuebin.Digital image correlation method based on particle swarm optimization algorithm without subpixel interpolation ［J］.Computer Engineering and Applications，2012，48 （6）：200－228 （in Chinese）.［杜亞志，王學(xué)濱.基于粒子群算法的整像素數(shù)字圖像相關(guān)方法 ［J］.計算機(jī)工程與應(yīng)用，2012，48 （6）：200－228.］