基于混沌理論的電力系統諧波檢測
李兆旸,劉崇新,燕并男
(西安交通大學 電氣工程學院,陜西 西安 710049)
電網中的諧波問題對電力系統的安全、穩定、經濟運行構成了極大的潛在威脅,為了能把注入公網的諧波電流以及諧波電壓控制到安全范圍內,首要解決的問題就是諧波檢測。諧波檢測的傳統方法主要有模擬濾波器測量諧波法,基于瞬時無功功率理論的諧波檢測法,基于傅里葉變換的諧波檢測法以及基于神經網絡理論的諧波檢測法等[1]。但是上述傳統方法中,由于信號中常常包含噪聲,其直接增大了仿真結果的誤差,影響了精確性。為此,通過混沌系統來檢測電力系統諧波信號,利用其對小信號極強的敏感性以及對噪聲的強免疫能力來解決傳統檢測方法中對噪聲抑制不徹底的不足之處,作為對現有諧波信號檢測方法中的一個補充是很有必要的。
混沌檢測不同于現有傳統的電力系統諧波檢測方法,它利用了混沌系統對于初值的極度敏感性,即我們可以考慮將h次諧波視為微擾信號,通過檢測系統狀態就可以根據其是否發生極大的變化來判定該諧波信號是否存在,若系統狀態變化時,還可以通過觀察系統狀態變化的特征,并對信號做出適當的處理以及運算,求出被測信號的各種參數[2-4]。
目前,Duffing振子[5]因其間歇混沌現象的特性常被用來作為檢測諧波信號的模型。具體來說,在Duffing方程右側加入與內置信號頻率差較小的待測信號時,內置信號幅值會出現相應變化,系統由于幅值的逐漸增大,會出現相應的間歇性混沌現象。即時而周期,時而混沌的運動狀態。經研究發現,當幅值的變化到達某一臨界值時(即系統出現臨界混沌狀態時),系統將在大尺度周期狀態和混沌狀態兩者之間振蕩,即會出現間歇性混沌現象,當幅值繼續增大時,系統將由間歇性混沌發展為混沌。
本文對Duffing振子方程進行了改進,分析了其產生的間歇混沌現象。通過仿真實驗證明:它對噪聲和與內置信號頻差較大的周期干擾信號具有較強的免疫力,并根據產生這種現象的機理,提出了一種新的有效檢測電力系統諧波信號的方法。
1 利用混沌性質檢測信號的原理
Duffing方程在非線性動力學系統具有重要的地位,根據其方程形式確定的混沌系統具有豐富的動力學特性。其具體形式如下:
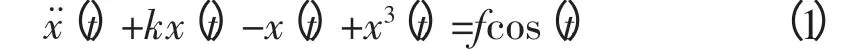
式中,x(t)為狀態變量;k為阻尼比;f為周期策動力幅值;-x(t)+x3(t)為非線性恢復力。
以往對Duffing方程檢測的研究中[6-11],使用的均是式(1)的方程形式。經對比發現,若將方程中的非線性恢復力項x冪項的系數增加,將顯著提升系統檢測信號的靈敏度以及工作穩定性。改正后的方程形式如下:
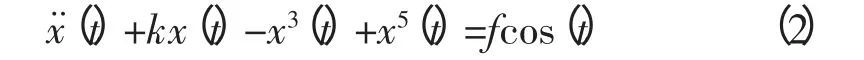
改寫為動力學方程:

對Duffing振子進行仿真分析,觀察其動力學行為。
若振子方程中的阻尼比k固定,則系統狀態隨著f 的變化如下:
f=0時,系統相軌跡圖中鞍點為(0,0),兩個焦點分別為(1,0)和(-1,0),而點(x,x.)最終停在兩焦點之一,如圖1所示。
當f≠0時,系統隨f 取值的不同而呈現出不同的動力學形態。當f 較小時,相軌跡表現為小周期運動狀態,相點只圍繞一個焦點做周期振蕩。f 逐漸增大的同時,系統會依次呈現出同宿軌道狀態(如圖2所示)和分叉狀態(如圖3所示),直到達到混沌狀態(如圖4所示),上述過程中f 的變化非常迅速。而在系統達到混沌狀態以后,調節策動力幅值時發現,系統在較大的一個區間內都將呈現出混沌狀態。繼續增大f,當其達到某個分叉閾值fd時,系統將會處于由混沌運動轉為周期運動的臨界狀態(又稱臨界混沌狀態),如圖5所示。這時只需極小地增加f,使其值僅僅大于分叉閾值fd時,系統就進入大尺度周期狀態,如圖6所示,此時相軌跡將焦點、鞍點統統圍住。
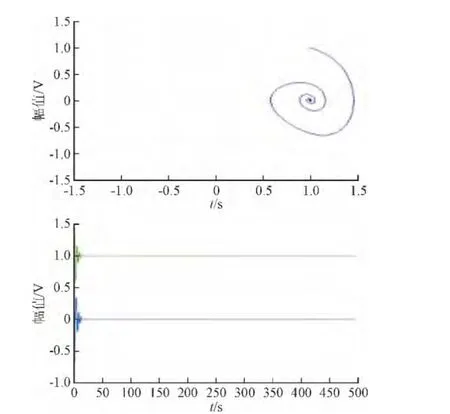
圖1 f=0,[x(0),x′(0)]=[1,1]Fig. 1 f=0,[x(0),x′(0)]=[1,1]

圖2 f=0.2,[x(0),x′(0)]=[0,0],w=1 rad/s同宿軌道狀態Fig. 2 f=0.2,[x(0),x′(0)]=[0,0],w=1 rad/s homoclinic orbit state
取阻尼比k=0.5,將策動力幅值從0逐漸增大,采用變步長ode45數值算法,即龍格庫塔方法進行仿真。各個狀態的時域波形圖以及相軌跡圖如圖1—6所示。
仿真結果表明了Duffing振子的動力學行為,并且從圖5到圖6的變化中可以看出,策動力幅值極其微小的變化(10-8)就能引起系統狀態產生質的變化。由以上分析可以得知,我們可以利用相軌跡由周期振蕩到混沌運動或者由混沌運動到周期振蕩的顯著變化來檢測信號,可以發現,這種變化對策動力信號幅值極具敏感性且對噪聲具有較強的免疫力等特點可以作為我們檢測諧波的基礎。據此,首先調節策動力幅值f,使Duffing振子系統處于混沌狀態向大尺度周期狀態過渡中的臨界混沌狀態,將諧波信號也就是待測信號作為Duffing振子周期策動力的擾動,將其相加從而作為驅動力。由于該系統對策動力的擾動極其敏感,通過觀察系統狀態發生改變與否,可以檢測出諧波信號是否存在,從而測定出該信號的參數。
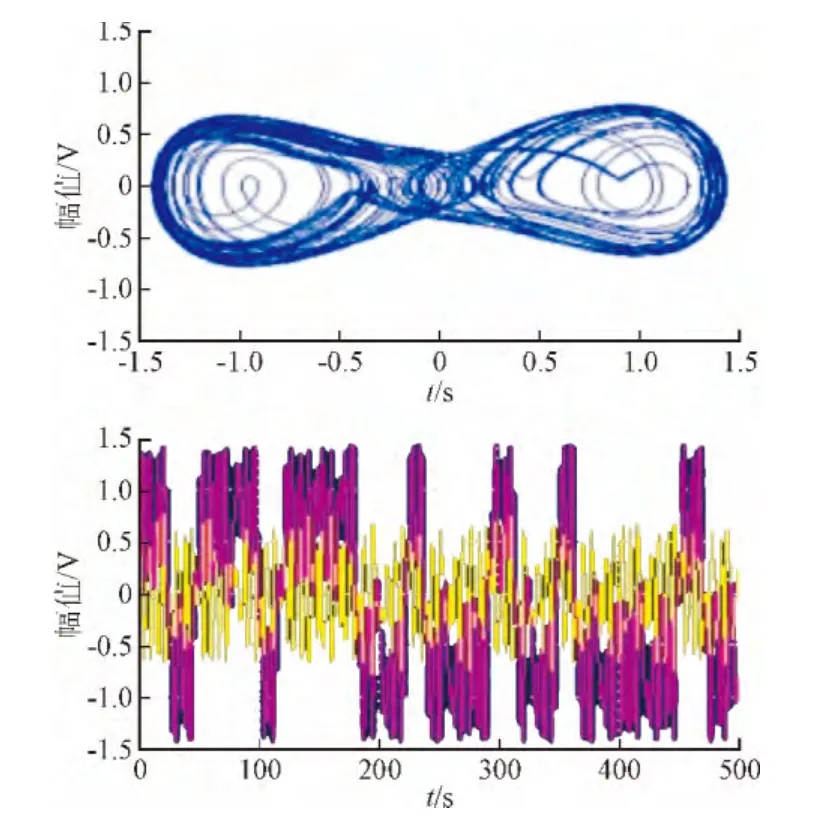
圖3 f=0.4,[x(0),x′(0)]=[0,0],w=1 rad/s分叉狀態Fig. 3 f=0.4,[x(0),x′(0)]=[0,0],w=1 rad/s bifurcation state

圖4 f=0.6,[x(0),x′(0)]=[0,0],w=1 rad/s混沌狀態Fig. 4 f=0.6,[x(0),x′(0)]=[0,0],w=1 rad/s chaotic state
2 測定信號參數
令t=ωτ,f=F0,式(1)可以改為:
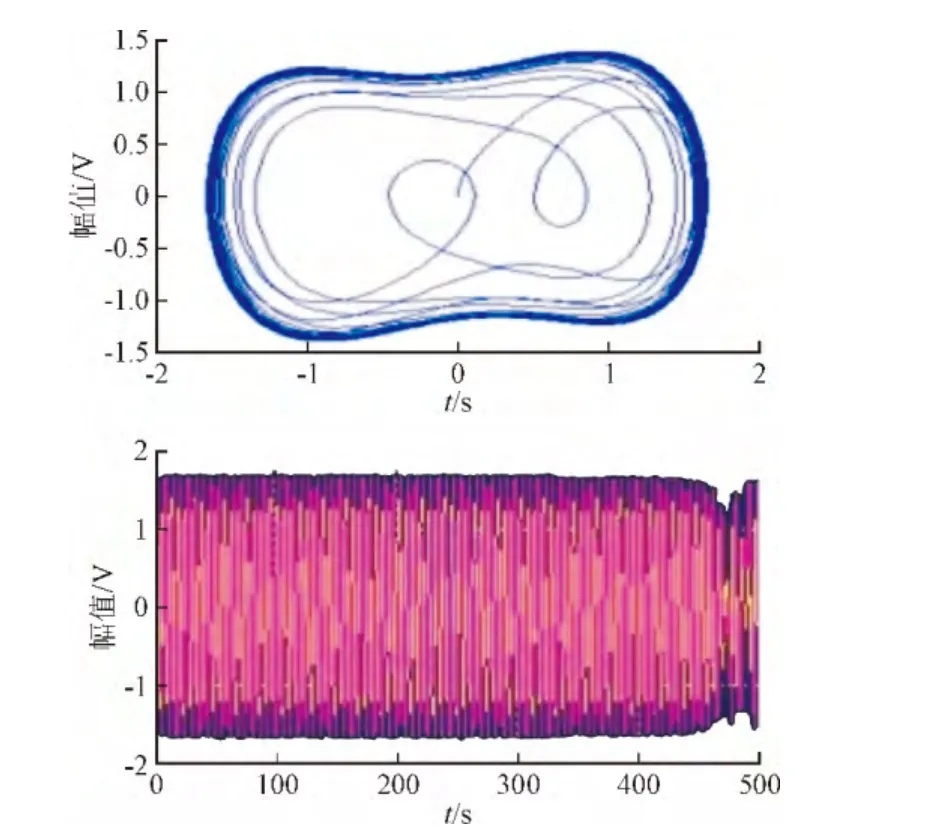
圖5 f=0.736 882 42,[x(0),x′(0)]=[0,0],w=1 rad/s臨界混沌狀態Fig. 5 f=0.736 882 42,[x(0),x′(0)]=[0,0],w=1 rad/s the critical state of chaos
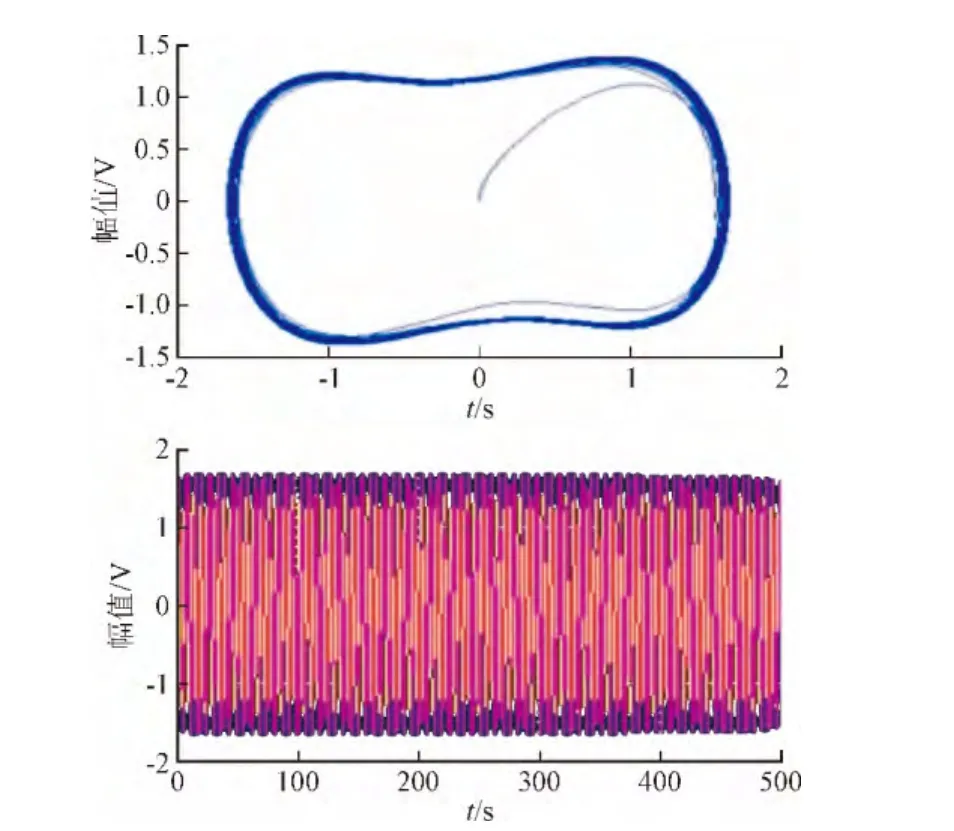
圖6 f=0.736 882 43,[x(0),x′(0)]=[0,0],w=1 rad/s大尺度周期狀態Fig. 6 f=0.736 882 43,[x(0),x′(0)]=[0,0],w=1 rad/s large-scale periodic state

在式(4)中右側加入頻率在ω附近的待測信號f′(t)=Acos[ω(1+Δω)t+φ],(Δω為待測信號與原有周期信號之間的相對頻差),得到:
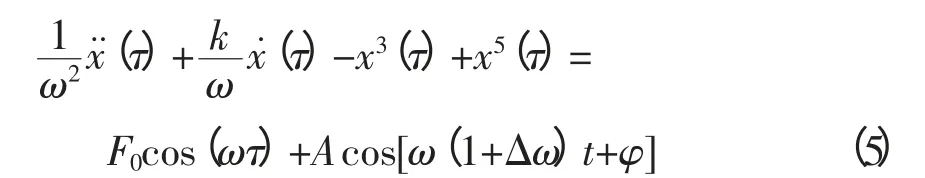
等號兩邊同時乘以ω2并對右側簡化,得到:
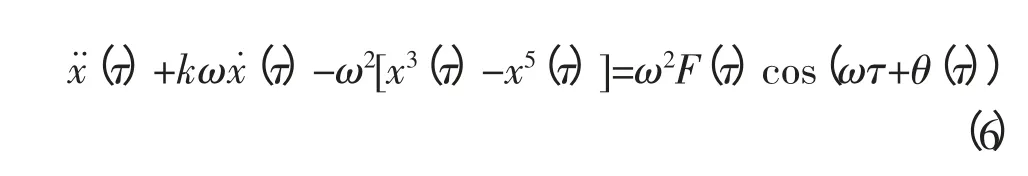
上式中

式中,F(τ)為驅動力的幅值;θ(τ)為驅動力的初相角。由于A塏F0,所以θ(τ)的影響可以忽略。
觀察式(6)與式(2)發現,二者差除了系數ω之外,前者比后者還多出了一個相位角參數。
據此,可得以下結論:
1)當Δω=0時,它表示此時待測信號頻率與周期策動力信號頻率相同。
2)當Δω≠0時,策動力信號頻率與振動信號頻率之間會有一個微小的頻差。此時總策動力F(τ)的幅值會在F(τ)∈(F0-A,F0+A)區間內周期性地交替變化,由于參考信號矢徑與外加信號矢徑方向趨于一致或方向相反時直接影響總驅動力F(τ)的幅值,即系統受F(τ)值的影響,時而大于fd而進入周期狀態,時而小于fd而進入混沌狀態,從而出現間歇性混沌現象。在微小的角頻差情況下,系統將以T=2π/Δω為周期,進行間歇性混沌運動。因此可以通過測量T,間接得到外界待測信號的頻率值。
取F0=0.72,A=0.04,ω=1.00,Δω=0.05,觀察系統變化情況。發現系統處于時而混沌運動,時而大尺度周期運動狀態,即出現間歇性混沌現象,如圖7所示。

圖7 Δω=0.05的間歇性混沌現象Fig. 7 Intermittent chaos in Δω=0.05
由圖7、圖8對比觀察,當待測信號與原有周期信號的相對頻率差值Δω過大時,間歇性混沌現象逐漸變得不明顯或者消失,因為系統完成狀態變化通常需要1個周期以上的時間,當Δω過大時,由式(7)決定的F(τ)變化過快,激勵不足以持續足夠長的時間,使得系統無法在狀態轉變時響應驅動力值F(τ)快速的變化,導致間歇性混沌現象不再規律性地出現。另外,當Δω過小時,F(τ)在相當長的一段時間內變化很小,導致系統狀態變化所需要的時間很長,即在一段長時間內維持周期狀態或混沌狀態。通過仿真實驗,我們一般取Δω∈(0.02,0.06)才能產生明顯的間歇性混沌現象。
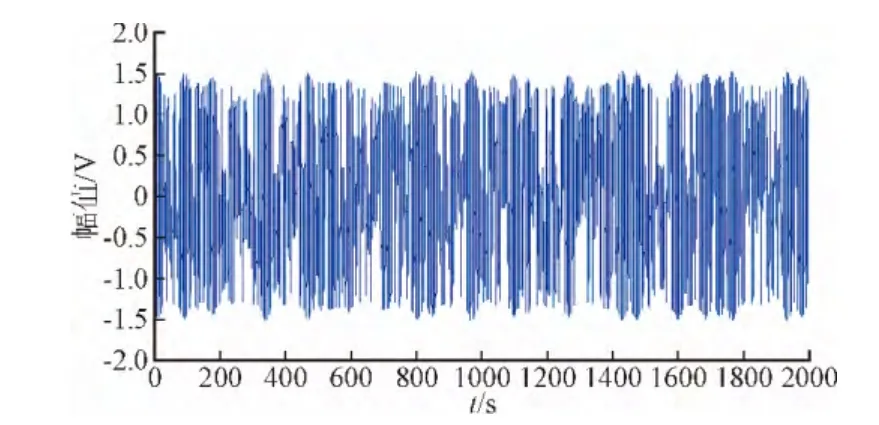
圖8 Δω=0.1的間歇性混沌現象Fig. 8 Intermittent chaos in Δω=0.1
2.1 測定信號的頻率

考慮到算法效率的問題,這里用統計系統變量過零時間點的間距方法來判斷系統運動的狀態。因為系統處于周期狀態時,過零時間點必然呈等差數列排列即間距相等,而處于混沌狀態時,則不具有這樣的特征。
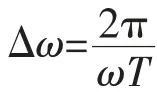
圖8的仿真和結論已經說明:當待測信號與周期策動力間的相對頻率差過大時,間歇性混沌現象消失。基于這一結論,要想測定某一已知頻率附近的擾動信號頻率,可以把周期信號設為該已知頻率,再來搜索確定該頻率附近是否存在小的擾動信號,即監測間歇性混沌現象是否發生。需要注意的是搜索區間大小一定要適中,過大或者過小都會導致無法監測到明顯的間歇性混沌現象。
例如要檢測頻率ω′∈(ω1,ω2)的待測信號,先選取合適的公比q=1+Δω,從ω1開始取ω′,ω′q,ω′q2等作為周期策動力的頻率,若發生間歇性混沌現象,就用上述方法算出ω′,若沒有發生間歇性混沌現象,則說明待測信號的頻率不屬于該預估區間內。
2.2 測定信號的相位
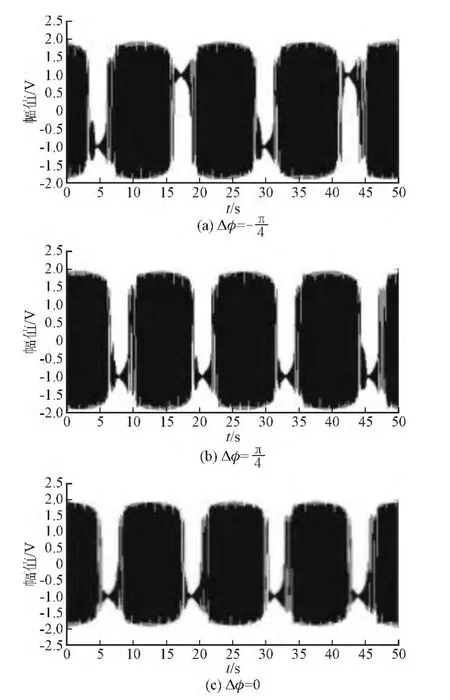
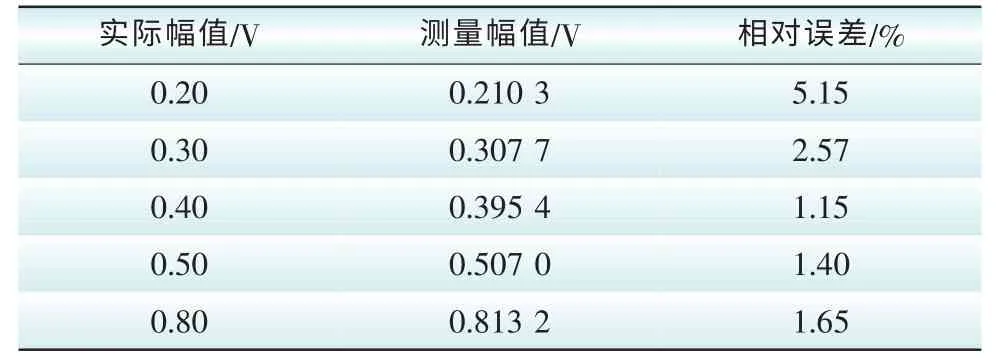
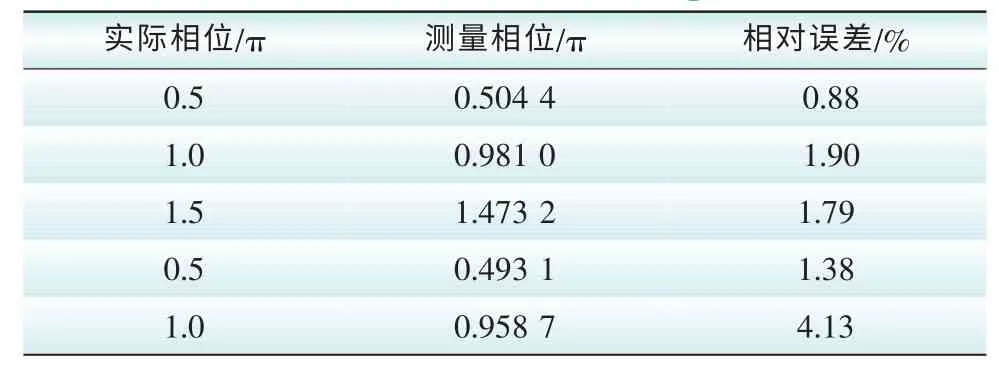
設當cos(ωΔωt+準)=a(a∈0,1)時,F(τ)=Fd(Fd為系統狀態變化的臨界值),則當cos(ωΔωt+準)>a時,系統會處于大尺度周期狀態,對應于圖9中的T1時間段;而當cos(ωΔωt+準) 圖9 系統分別處于大尺度周期和混沌狀態的時間段Fig. 9 System in Large-scale periodic state and chaoticstate period 設式(5)中的周期策動力為F0cos(ωt+準1),待測信號Acos(ω(1+Δω)t+準2),二者相位差Δ準=準2-準1,F(τ)和θ(τ)均有變化: 不妨設相位差Δ準=0,當t=0時,cos(ωΔωt+Δ準)=1,F(τ)=F0+A>Fd,系統處于大尺度周期狀態,隨著時間的變化,ωΔωt+Δ準=T1時,cos(ωΔωt+Δ準)減小到a,F(τ)從F0+A減小到Fc,系統處于從大尺度周期狀態進入混沌狀態的臨界狀態。同樣的,如果cos(ωΔωt+準)從a增加到1,相應的F(τ)從Fc增加到F0+A,不難發現,該過程同樣需要時間T1。 圖10 Δφ不同時的間歇性混沌現象Fig. 10 Intermittent chaos in different phase Δφ 待測信號相位準2=準1+Δ準。 觀察圖9可得: 上兩式中,T1為大尺度周期狀態的持續時間;T2為混沌狀態的持續時間。 通過過零點間距方法找出大尺度周期狀態和混沌狀態的持續時間T1和T2,代入式(14)中解關于幅值A的一元二次方程,即可得到未知信號幅值的大小。 仿真試驗中的振子實驗結構如圖11所示。 圖11 振子的系統仿真模型Fig. 11 Oscillator system simulation model 當將待測信號加入原有周期信號之后,通過檢測間歇性混沌信號,并用上述方法得出待測信號的幅值。仿真時,設定k=0.3,取[x(0),x′(0)]=[0,0],利用定步長h=0.01四階龍格—庫塔方法進行計算。以下表1~表3即是仿真后所測得的信號參數。 表1 待測信號幅值Tab. 1 Amplitude of tested signal 表2 待測信號相位Tab. 2 Phase of tested signal 由仿真結果可以看出,絕對誤差的總體趨勢是隨著測量值增加而線性上升的,而相對誤差則一直維持在一個較小的值,計算結果的誤差達到了測量的預期。理論上只要選擇合適的參數以及算法,測量的精度上限可以無窮逼近實際值。 表3 待測信號頻率Tab. 3 Frequency of tested signal 通過以上仿真分析,利用混沌系統檢測電力諧波較之于傳統電力系統檢測方法精度更高,抗噪性更強,而當多頻信號檢測時,只需要調整振子參數,就可以實現檢測。同時,修改方程后的振子系統比傳統的Duffing振子系統對周期性小信號更具有敏感性,能夠得到更大的幅值有效區間和更高的精度。若能夠有效地將該方法與其他方法相結合,優勢互補,將會使得利用混沌理論檢測電力系統諧波走向實際應用。 [1] 李圣清,朱英浩,周有慶,等. 電網諧波檢測方法的綜述[J]. 高電壓技術,2001,30: 39-42.LI Shengqing,ZHU Yinghao,ZHOU Youqing,et al. The overview of detecting methods for harmonic in power system[J]. High Voltage Engineering,2001,30: 39-42(in Chinese). [2] OTT E GREBOGI C,YORKE A. Controlling chaos[J].Phys Rev Lett A,1990,64: 1796-1799. [3] YANG J Z,QU Z L,HU G. Duffing equation with two periodic forcings: The phase effect[J]. Phys Rev Lett A,1996,53(5). [4] 柴旭生,文習山,關根志. 一種高精度的電力系統諧波分析方法[J]. 中國電機工程學報,2003,23(9): 35-39.CHAI Xusheng,WEN Xishan,GUAN Genzhi. A high precision method for power system harmonic analysis[J].Proceedings of the CSEE,2003,23(9):35-39(in Chinese). [5] 翟篤慶,劉崇新,劉堯,等. 利用陣發混沌現象測定位置信號的參數[J]. 物理學報,2010,59(2): 816-825.ZHAI Duqing,LIU Chongxin,LIU Yao,et al. Determination of the parameters of unknown signals based on intermittent chaos[J]. Acta Physica Sinica,2010,59(2):816-825(in Chinese). [6] HUANG J C,JING Z J. Bifucation and chaos in the three-well Duffing system with one external forcing[J].Chaos,Solitons & Fractals,2009,40(3): 1449-1466. [7] 李月,楊寶俊,石耀武. 色噪聲背景下微弱正弦信號的混沌檢測[J]. 物理學報,2003,52(3):526-530.LI Yue,YANG Baojun,SHI Yaowu. Chaos-based weak sinusoidal signal detection approach under colored noise background[J]. Acta Physica Sinica,2003,52(3): 526-530(in Chinese). [8] WANG Guanyu,CHEN Dajun,LIN Jianya. The application of chaotic oscillators to weak signal detection[J]. IEEE Transactions on Industrial Electronics,1999,46(2): 440-444. [9] 王永生,肖子才,孫瑾,等. Duffing混沌系統電路仿真研究[J]. 電力與系統學報,2008,13(1): 133-135.WANG Yongsheng,XIAO Zicai,SUN Jin,et al. Simulation and experimental study on the chaos circuit of Duffing oscillator[J]. Journal of Circuit and System,2008,13(1):133-135(in Chinese). [10] 聶春燕,徐振忠. 混沌系統在弱檢測信號檢測中的應用[J]. 傳感器技術,2003,22(1): 55-57.NIE Chunyan,XU Zhenzhong. Application of chaotic system in detecting weak signal[J]. Journal of Transducer Technology,2003,22(1): 55-57(in Chinese). [11] 朱志宇,姜長生,張兵,等. 基于混沌理論的微弱信號檢測方法[J]. 傳感器技術,2005,24(5): 65-68.ZHU Zhiyu,JIANG Changsheng,ZHANG Bing,et al.Weak signal detection based on chaotic theory[J]. Journal of Transducer Technology,2005,24(5):65-68(in Chinese).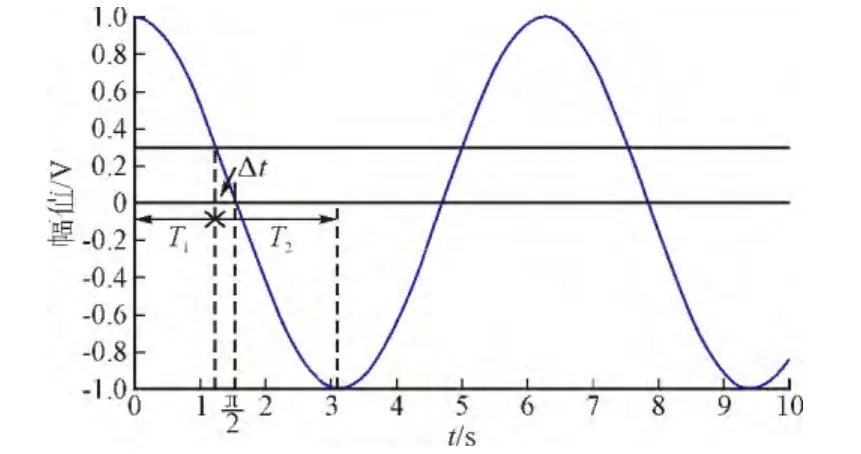
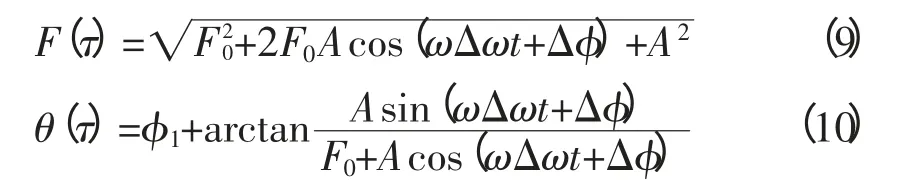

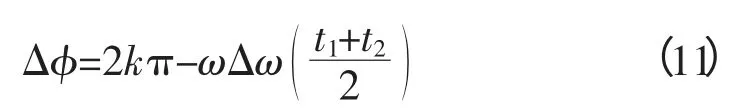
2.3 測定信號幅值
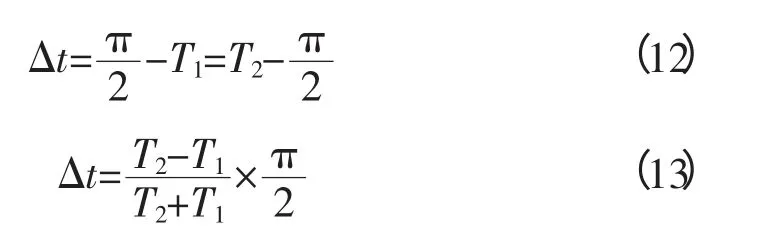


3 仿真結果


4 結論

