基于迭代凸優化的恒模波形合成方法

李秀友 薛永華 董云龍 關 鍵

1 引言

認知雷達是未來雷達發展的主要方向之一，認知雷達由于引入了閉環反饋結構，可以根據獲取的場景信息自適應調整發射波形，從而改善系統性能[1]。波形設計是認知雷達關鍵技術之一，波形優化設計是在一定的約束條件下最大化準則函數，準則函數的選取取決于雷達系統的任務和工作模式[26]-。

大量文獻研究了認知雷達的波形優化問題。文獻[7]首先提出了利用目標和回波的最大互信息設計發射波形，從信息論角度解決波形優化問題。文獻[8]研究了基于距離擴展目標最大輸出信雜噪比的波形設計方法，設計得到最優發射波形和接收濾波器的功率譜。文獻[9]分析了廣義平穩高斯雜波中點目標的檢測問題，將回波信號統一變換到頻域，再根據對數似然比檢測器的最大檢測概率準則，用“注水法”求得最優發射波形能量譜。

以上最優波形設計算法只能得出優化波形的能量譜，要應用于實際雷達系統還需要合成時域波形，為了提高發射機功率利用率，常需要合成滿足能量譜約束的恒模波形。目前基于波形能量譜合成時域信號常用的有3種方法，分別是Durbin 法、駐留相位法[10]和迭代合成法[11]。Durbin法相對簡單，但不能滿足恒模要求，駐留相位法合成波形具有恒模特性，但是無法很好地擬合復雜形狀能量譜，迭代算法收斂速度慢，能量譜邊沿擬合誤差大。

滿足給定能量譜的恒模波形設計問題需要同時在頻域滿足給定頻譜，在時域滿足恒模要求[11]。這類約束在兩個不同集合中的優化問題常采用交替投影法，這種處理方法廣泛應用于約束條件下的波束形成和時域波形合成中[1214]-。此類問題求解通常采用迭代方法在兩個不同集合之間交替投影，逐步逼近滿足約束條件的解，該解存在于兩個集合的交集中[15]。以上迭代方法在不同集合中以各自約束條件為目標函數進行優化處理，而不考慮相互之間的影響，這種處理方法往往會導致整體收斂速度變慢，收斂到性能較差的局部最優值[16]。文獻[17]在設計滿足峰均功率比（Peak-to-Average Power Radio,PAPR）約束的正交頻分復用（OFDM）信號時，將信號頻域失真和時域PAPR約束聯合優化，使得每步優化過程能夠同時兼顧兩個約束條件，提高了收斂速度，降低了誤碼率。

受上述思路的啟發，本文在文獻[11]迭代波形合成算法的基礎上，將頻譜逼近過程構造成約束條件下的優化問題，其中時域恒模特性作為約束條件，波形能量譜與期望能量譜的誤差作為目標函數。在優化處理過程中將恒模約束放松為PAPR約束，并對頻譜進行加權處理，進一步降低阻帶內功率水平，然后通過一系列變換操作將優化問題轉化成二階錐規劃（Second-Order Cone Programming, SOCP）問題求解，最后通過仿真結果驗證算法的有效性。

2 經典時域波形合成算法

給定期望的N點幅度譜密度函數s（k）, 0k= ,1,,1N-…，需要設計M點單位幅值恒模復信號：如果M＜N，則x（n）補零到N點，使得x（n）的N點DFT變換y（k）接近期望的幅度譜s（k）。

為使得設計的恒模信號幅度譜接近期望值，設y（k）的相位為φ（k），則最小二乘誤差可寫為

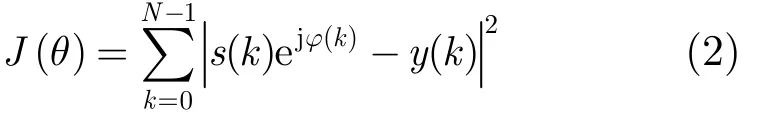
定義 s =

s（ 0）ejφ（0）,s （ 1）ejφ（1）,… ,s （ N - 1）e，并定義 x =[x （ 0）,x （ 1）,… ,x （ N - 1）]T，則式（2）經過一系列變換可以得到x的最小二乘估計值，并將時域信號估計值x做幅度歸一化處理，即得到恒模的時域信號。

其中arg（）?表示取相位，文獻[11]將上述兩步估計構成迭代算法，將第i次迭代的幅度譜相位估計值（）（）ik φ 直接賦給期望幅度譜，即

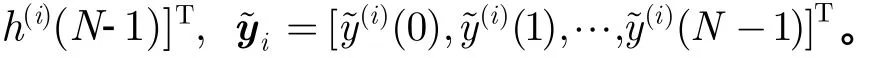
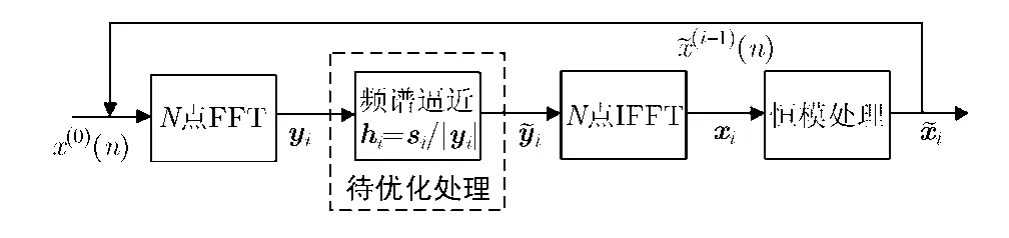
圖 1 基于頻譜最小二乘誤差的恒模波形合成法

上述算法在頻譜逼近處理過程中，直接將期望幅度譜s（k）作為下一次迭代的頻譜幅值，沒有考慮到做IFFT之后時域信號的峰值大小。時域不做約束的頻譜逼近處理將會導致時域信號出現較大的峰值，需要多次迭代才能得到滿足恒模和幅度譜逼近的波形，降低了收斂速度。該算法將設計波形幅度譜和期望幅度譜的整體誤差作為代價函數，沒有重點考慮阻帶內頻譜誤差對性能的影響。而波形阻帶部分通常是強雜波或強干擾所在頻段，需要設計較深的凹口來提高信雜比或信干比。

3 加權迭代優化波形合成算法

本文提出的算法是在文獻[11]迭代算法（下文簡稱Kay算法）的基礎上，針對頻譜逼近過程存在的不足進行改進。首先，構造波形時域PAPR約束條件下的優化表示式，同時兼顧幅度譜逼近程度和時域起伏大小；然后對頻譜矢量加權處理，抑制阻帶內發射功率水平；最后將優化問題轉換成二階錐規劃（SOCP）問題，利用內點法求解。

3.1 建立滿足約束條件的目標函數

此處定義時域信號PAPR：

其中 ?2表示2-范數，?∞表示無窮范數。定義1維加權矢量w=[w（0）,w（1）,…,w（N-1）]T，引入頻譜加權誤差矢量值（Weighted Error Vector Magnitude,WEVM）用于表征兩個頻譜矢量加權誤差大小，表達式為其中，運算符號‘·’表示對應元素乘積。

上述迭代波形合成算法中直接將期望幅度譜s（k）作為下一次迭代輸入信號頻譜的幅值，這會導致合成信號的幅值出現大的波動，使得迭代收斂速度變慢，且每步迭代過程沒有最優準則保證。本文提出了在PAPR約束下的加權誤差矢量值（WEVM）最小化算法：

由于約束函數式（7d）為非凸的，優化模型式（7）也是非凸的，這使得其數值求解比較困難。

3.2 基于SOCP的波形優化設計

為將優化問題式（7）修正成凸的表達式，用xi-122近似替換xi22，則非凸約束式（7d）可以變換成[17]

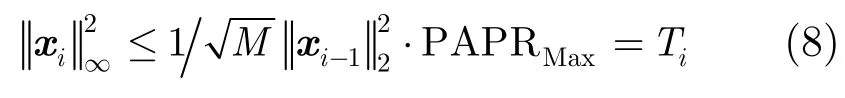
由于在第i次迭代過程中xi-122是已知的，PAPRMax為預先設置的參數，則每次迭代過程中約束峰值Ti可以計算求得，因而非凸約束轉化成凸約束式（8）。其中，當PAPRMax值足夠大時，約束條件式（7d）失效，優化算法退化為文獻[11]最小二乘估計算法。優化模型式（7）可以簡化為

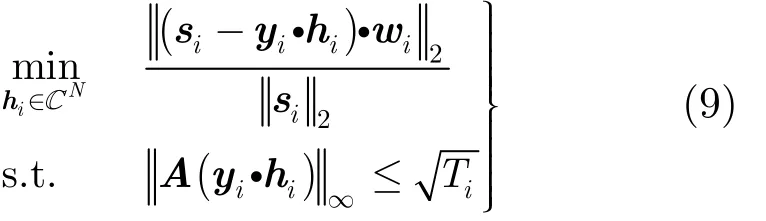
其中，矩陣A由N維IFFT旋轉因子矩陣的前M行構成，式（9）可以進一步表示成二階錐規劃（SOCP）[18,19]

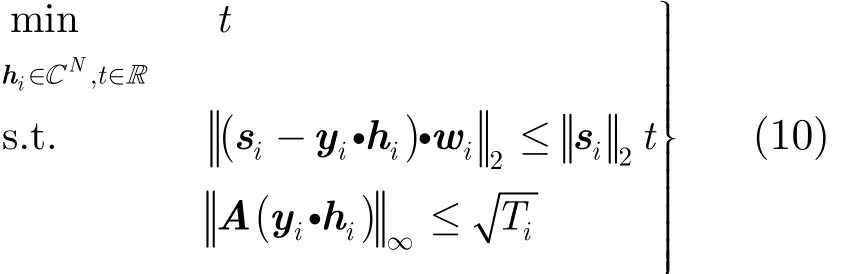
3.3 加權優化迭代波形合成算法

加權優化迭代波形合成算法流程如圖2所示，主要包括PAPR約束下的最優幅度譜加權逼近處理和信號幅度恒模處理過程。定義相鄰兩次迭代過程時域波形變化量。

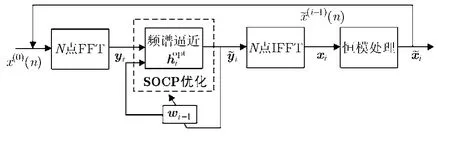
圖 2 加權優化迭代波形合成流程圖

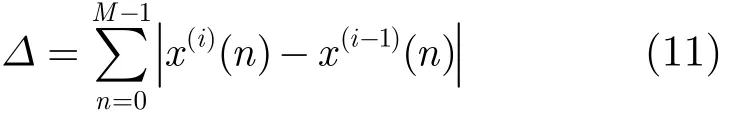
其中x（i）（n） 表示第i次迭代時域估計值。具體迭代步驟如下，其中步驟1用于初始化，步驟2至步驟7循環迭代直至終止。

步驟 1 初始化過程，設定峰均功率比PAPRMax和加權系數矢量w；

步驟 2 如果i=1，則令 x（0）（n ） = exp（jθn（0）） ，其中 k =0,1,… ,M -1,θn（0）為隨機產生的相位，服從[- π, π]上 的 均 勻 分 布 ， 當i≠1時 ， 令x~（i）（n）=x~（i-1）（n），利用FFT將 x~i變換到N點離散頻域形式yi=[y（i）（0）,y（i）（1）,… ,y（i）（N-1）]；

步驟 3 執行約束條件下的加權優化算法式（10），得到最優逼近濾波器hi，并令 y~i=yi. hi；

步驟 4 根據 y~i值自適應調整加權系數 wi-1，控制阻帶整體功率水平或峰值頻點功率；

步驟 5 利用IFFT將 y~i變換到時域信號xi；

步驟 6 利用式（3）對信號xi幅值做歸一化處理，得到恒模的時域信號 x~i；

步驟 7 當 Δ ＜ 0 .01 × M 時，循環終止，否則返回步驟2。

3.4 算法復雜度分析

SOCP模型可以用標準內點法求解，優化模型最差情況下的運算量為O（N3）[18]，每次迭代過程中，包含一次FFT和IFFT運算，運算量為O（Nlog2（N）），阻帶內峰值搜索及信號歸一化處理運算量為O（N）。當最大迭代次數為P時，所提算法整個運算量為O（PN3+PNlog2（N）+PN）。

4 仿真結果及性能分析

下文通過計算機仿真驗證本文算法的有效性和優越性。為便于比較分析，本文仿真設計與文獻[11]相同能量譜密度的最優雷達發射波形，表示式為

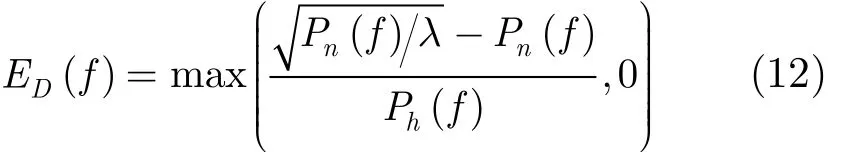
其中， Pn（f）為噪聲功率譜密度， Ph（f） 為雜波功率譜密度，λ為由能量約束決定的常數。仿真中最優能量譜密度設為100個頻點，對應的能量譜如圖3所示。從圖中可以看出，在部分頻點上信號能量譜較大，以下簡稱為通帶頻段，在其余頻點上能量為零，為強干擾區或雜波區，簡稱阻帶頻段。希望設計的波形在恒模約束下與最優波形的能量譜最接近，其中過渡頻帶的擬合程度最能反應波形的逼近性能，阻帶凹口深度決定了所設計波形對強雜波及干擾的抑制能力。

因此，以下仿真分析將從算法收斂速度，阻帶內整體能量大小，峰值功率水平以及過渡頻段的頻譜擬合程度等方面綜合分析算法的性能。

4.1 固定權系數抑制阻帶能量

為了分析權系數w=[w（0）,w（1）,…,w（N-1）]T對阻帶凹口的影響，令阻帶內對應頻點上的權重為10 dB，通帶內對應頻點權系數為0 dB，權系數表示為

其中固定權系數在每次迭代過程中保持不變，權系數的設定在4.3節中說明。圖4（a）給出了本文固定權系數優化算法與Kay算法的能量譜，當迭代次數P=200時，在阻帶內大部分頻點上，本文優化算法功率低于Kay算法，圖4（b）給出了50次仿真能量譜的平均值，阻帶內各頻點上本文優化算法低于Kay算法。圖5給出了兩種算法阻帶內積分能量隨迭代次數變化曲線，本文算法比Kay算法阻帶內能量下降快且低5.3 dB；分析10次和50次仿真結果平均值可以看出不同初始相位對收斂結果略微有影響，但是不會改變算法的整體收斂性；由于迭代過程中對時域波形的恒模處理，收斂曲線局部無法保證單調下降，大量仿真實驗表明，局部非單調不影響整體收斂趨勢。圖6給出了不同波形長度兩種算法累積能量譜密度，本文算法跟期望累積能量譜密度曲線比較接近，在邊緣區域也比Kay算法更接近理想曲線。其中累積能量譜密度定義為

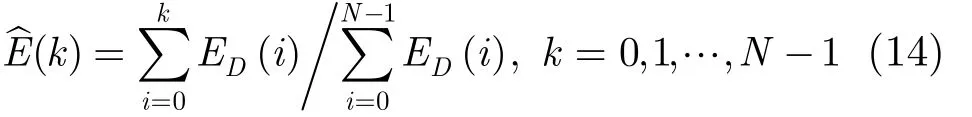
根據式（11）的收斂條件，當波形長度M=20, 50和100時，收斂所需的迭代次數分別為7次，8次和10次。可以看出本文算法和Kay算法的累積能量譜密度均隨著波形長度M的增加而逼近理想值，且在不同M值時，本文算法優于Kay算法。

4.2 自適應調整權系數抑制阻帶內峰值頻點

固定權系數無法控制阻帶內頻點的峰值能量，為了降低整個阻帶頻點上的能量，在每次迭代過程中，搜索阻帶內頻譜峰值點，將該對應點的權系數增大到20 dB，其余點權系數不變，如式（15）所示。通過優化設計降低該頻點的能量，經過反復迭代，阻帶內所有頻率點的能量得到有效控制。圖7給出了兩種算法在相同初始相位時，經過200次迭代所得恒模波形的能量譜，本文優化迭代算法阻帶內最大峰值功率降為0.4 dB，比通帶低21.6 dB，比Kay算法阻帶內峰值功率6.8 dB低6.4 dB。圖8給出了阻帶內能量隨著迭代次數收斂情況，該算法能有效收斂，且本文算法比Kay算法阻帶能量低5.8 dB，同時給出了10次和50次仿真結果平均值，可以看出不同初始相位對收斂過程有一定影響，但是不會改變算法的收斂趨勢。迭代循環終止準則按照式（11），則不同信號長度M的收斂次數跟固定權系數算法相近。

4.3 權系數設定及運算量分析

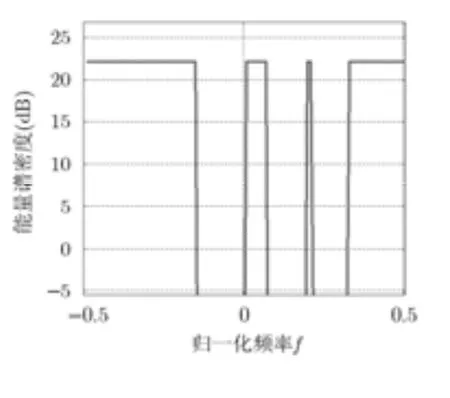
圖 3 最優發射波形能量譜密度

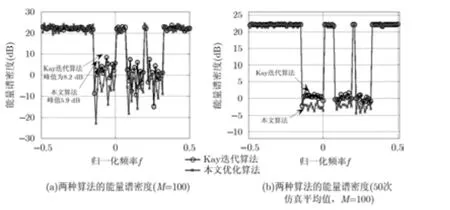
圖 4 固定權系數波形性能分析（PAPRMax=0.5 dB）

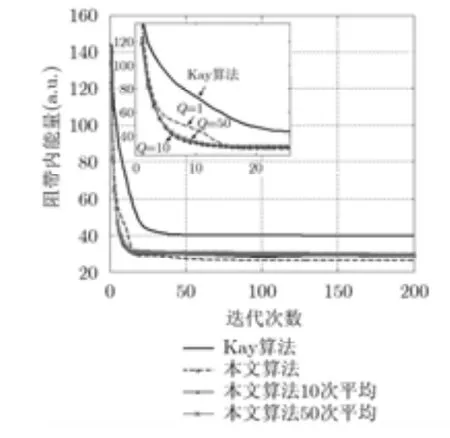
圖 5 固定權系數算法阻帶內積分能量隨迭代下降曲線（仿真次數Q=1,10和50的平均值, M=100, PAPRMax=0.5 dB）

圖 6 波形累積能量譜密度曲線 （波形長度M=20,50,100）

圖 7 自適應權系數設計的波形能量譜（PAPRMax=0.5 dB, M=100）

下面主要討論權系數w對阻帶內積分能量和峰值的影響，圖9給出了50次仿真平均值。從圖9（a）可以看出，當固定權系數w在0～10 dB變化時，阻帶內積分能量呈下降趨勢，當超過10 dB時變化不顯著，因此仿真中固定權系數選為10 dB。圖9（b）給出了當阻帶權系數定為10 dB條件下，峰值功率水平與峰值位置自適應權系數的關系，當自適應權系數超過20 dB時，峰值功率水平震蕩起伏變化，因此仿真過程中自適應權系數選為20 dB是合理值。

表1給出了不同算法的運算量，由于引入SOCP模型，用標準內點法求解優化模型最差情況下的運算量為O（N3），本文算法運算量有所增加，所以該方法更適用于對波形頻譜逼近程度要求較高的短波形設計或對實時性要求不高的長波形設計。

5 結論

本文提出了一種基于迭代凸優化的恒模波形合成方法，該方法將波形合成過程轉化成PAPR約束下的優化問題，減少了迭代收斂次數，并利用頻譜加權處理降低阻帶功率水平，提高干擾及強雜波抑制能力，最后通過一系列變換操作將優化問題轉化成二階錐規劃（SOCP）問題求解。所提方法在給定波形能量譜的條件下能夠有效逼近理想的頻譜形狀，設計的波形具有恒模特性，并且適用于頻譜形狀較復雜的波形，最后通過計算機仿真驗證了本文算法的有效性。

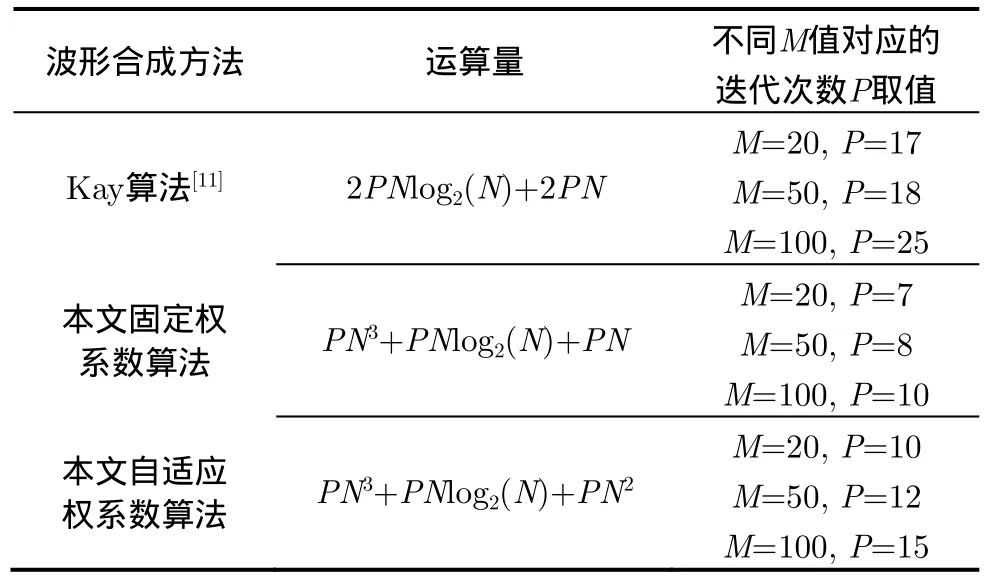
表 1 波形合成方法運算量比較

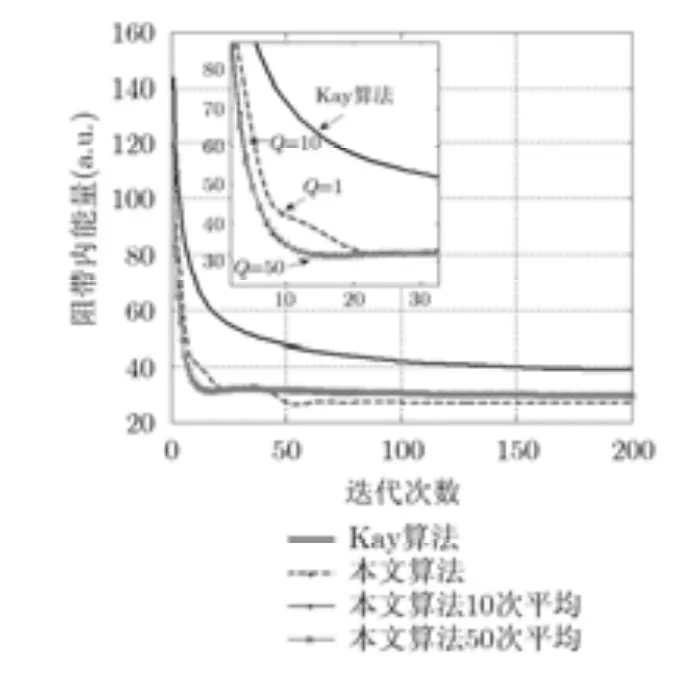
圖 8 自適應權系數算法阻帶內積分能量隨迭代下降曲線（仿真次數Q=1, 10和50的平均值，M=100）

圖 9 阻帶內能量和峰值與 權系數關系

[1] Haykin S. Cognitive radar: a way of the future[J]. IEEE Signal Processing Magazine, 2006, 23（1）: 30-40.

[2] Sen S. PAPR-constrained pareto-optimal waveform design for OFDM-STAP radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52（6）: 3658-3669.

[3] Zhang X and Cui C. Signal detection for cognitive radar[J].Electronics Letters, 2013, 49（8）: 559-560.

[4] Aubry A, De Maio A, Jiang Bo, et al.. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]. IEEE Transactions on Signal Processing,2013, 61（22）: 5603-5619.

[5] Aubry A, De Maio A, Farina A, et al.. Knowledge-aided（potentially cognitive） transmit signal and receive filter design in signal-dependent clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49（1）: 93-117.

[6] 公緒華, 孟華東, 魏軼旻, 等. 雜波環境下面向擴展目標檢測的自適應波形設計方法[J]. 清華大學學報, 2011, 51（11）:1652-1656.Gong Xu-hua, Meng Hua-dong, Wei Yi-min, et al.. Adaptive waveform design for range-spread target detection in clutter[J]. Journal of Tsinghua University （Science &Technology）, 2011, 51（11）: 1652-1656.

[7] Bell M R. Information theory and radar waveform design[J].IEEE Transactions on Information Theory, 1993, 39（5）:1578-1597.

[8] Romero R A, Bae Junh-yeong, and Goodman N A. Theory and application of SNR and mutual information matched illumination waveforms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47（2）: 912-927.

[9] Kay S. Optimal signal design for detection of Gaussian point targets in stationary Gaussian clutter/ reverberation[J]. IEEE Journal of Selected Topics in Signal Processing,2007, 1（1）: 31-41.

[10] Richards M A. Fundamentals of Radar Signal Processing[M].New York: The McGraw-Hill Companies, 2005: 230-231.

[11] Leland J, Steven K, and Naresh V. Iterative method for nonlinear FM synthesis of radar signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010,46（2）: 910-917.

[12] 趙宜楠, 李風從, 王軍, 等. 基于秩虧傅里葉變換的交替投影編碼波形設計[J]. 電子學報, 2014, 42（6）: 1216-1219.Zhao Yi-nan, Li Feng-cong, Wang Jun, et al.. Coded waveform design via alternating projection based on rank deficient Fourier transform[J]. Acta Electronica Sinica, 2014,42（6）: 1216-1219.

[13] 李風從, 趙宜楠, 喬曉林. 抑制特定區間距離旁瓣的恒模波形設計方法[J]. 電子與信息學報, 2013, 35（3）: 532-536.Li Feng-cong, Zhao Yi-nan, and Qiao Xiao-lin. Constant modular waveform design method for suppressing range sidelobes in specified intervals[J]. Journal of Electronics &Information Technology, 2013, 35（3）: 532-536.

[14] 趙宜楠, 張濤, 李風從, 等. 基于交替投影的MIMO雷達最優波形設計[J]. 電子與信息學報, 2014, 36（6）: 1368-1373.Zhao Yi-nan, Zhang Tao, Li Feng-cong, et al.. Optimal waveform design for MIMO radar via alternating projection[J]. Journal of Electronics & Information Technology, 2014, 36（6）: 1368-1373.

[15] Vescovo R. Reconfigurability and beam-scanning with phase-only control for antenna arrays[J]. IEEE Transactions on Antennas and Propagation, 2008, 56（6）: 1555-1565.

[16] Armstrong J. Peak-to-average power reduction for OFDM by repeated clipping and frequency domain filtering[J].Electronics Letters, 2002, 38（5）: 246-247.

[17] Wang Y C and Luo Z Q. Optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J]. IEEE Transactions on Communications, 2011, 59（1）: 33-37.

[18] Boyd S and Vandenberghe L. Convex Optimization[M].Cambridge, United Kingdom: Cambridge University Press,2004: 340-341.

[19] Lobo M, Vandenberghe L, Boyd S, et al.. Applications of second-order cone programming[J]. Linear Algebra and Its Applications, 1998, 11（284）: 193-228.