基于變參數(shù)隨機共振和歸一化變換的時變信號檢測與恢復

張海濱 何清波 孔凡讓

1 引言

在傳統(tǒng)的觀念上，噪聲總是被認為起破壞作用的。但是近二十年非線性理論和實驗揭示，對許多非線性系統(tǒng)來說，適當?shù)脑肼暩蓴_反而可以幫助系統(tǒng)提高信號輸出的能力，這類現(xiàn)象即為隨機共振（Stochastic Resonance, SR），其最初是在文獻[1]中用來解釋過去70萬年地球的冰川期和暖氣候期交替出現(xiàn)的現(xiàn)象。根據(jù)隨機共振理論，當淹沒在強背景噪聲中的微弱信號通過某種非線性系統(tǒng)時，在噪聲與信號的協(xié)同作用下會發(fā)生噪聲能量向信號能量轉移，使非線性系統(tǒng)的輸出信噪比得到增強[2,3]。由于信號的輸出信噪比隨噪聲的增大呈現(xiàn)先增后減的趨勢，并在某一噪聲強度值時出現(xiàn)峰值，產(chǎn)生類似力學中人們熟知的共振輸出現(xiàn)象，故稱為隨機共振。正是由于隨機共振能夠提高含噪微弱信號的輸出信噪比，人們將隨機共振引入微弱信號檢測[36]-、機械故障診斷[79]-、能量回收[10,11]等領域。

但是不難發(fā)現(xiàn)，在所有的隨機共振應用領域中，用于驅動系統(tǒng)的信號都具有固定周期，即輸入信號都是由周期信號和噪聲所構成。但是在實際應用中，經(jīng)常會遇到一些非周期性信號（aperiodic signal），比如線性調(diào)頻（Linear Frequency Modulated, LFM）信號、非線性調(diào)頻信號（NonLinear Frequency Modulated, NLFM）、多普勒（Doppler）信號等等。這些非周期信號在無線通信、雷達、聲信號處理等領域都廣泛存在，而且這類信號同樣容易受到噪聲的污染使其不容易被探測和甄別，特別對于LFM信號的檢測和恢復也同樣面臨巨大挑戰(zhàn)[12,13]。鑒于隨機共振系統(tǒng)對微弱信號探測的優(yōu)勢，所以為了能夠利用隨機共振處理一些非周期信號，必須將輸入信號推廣到具有有限帶寬的非周期信號中去。1995年以來，國內(nèi)外學者對非周期隨機共振作了大量研究[14,15]；國內(nèi)也有一些研究人員利用傳統(tǒng)的隨機共振對周期信號的放大作用，將其用于線性調(diào)頻信號的參數(shù)估計和信號恢復[16,17]。在利用隨機共振處理非周期驅動信號時，由于非周期信號不再具有確定的頻率，因此不能再用信噪比來度量，文獻[16]提出了基于分數(shù)階傅里葉變換的分數(shù)階信噪比（Fractional Signal-to-Noise Ratio, FrSNR），但是這個只適用于線性調(diào)頻信號，他們在某個確定的方向上仍然具有頻譜能量集中的特點，對于其他的非周期信號則不適用，而且，目前對于非周期隨機共振的研究模型，由于受到絕熱近似條件的約束，輸入信號仍然需要滿足小參數(shù)條件，這就限制了模型在一些實際場合的應用。

出于以上幾點考慮，本文采用四階 Runge-Kutta數(shù)值求解的數(shù)值仿真分析，基于雙穩(wěn)態(tài)隨機共振模型參數(shù)的歸一化變換[18]，提出了一種變參數(shù)隨機共振（Variable Parameters SR, VPSR）模型。該模型首先將系統(tǒng)參數(shù)進行歸一化變換使其適應于高頻輸入信號；然后以輸出信號的擬合決定系數(shù)及其和輸入信號的互相關系數(shù)作為評判標準，得到時變信號的頻率變化參數(shù)，利用該參數(shù)決定VPSR的系統(tǒng)參數(shù)變化規(guī)律；最后尋找系統(tǒng)參數(shù)的最優(yōu)初始值，得到隨時間變化的最優(yōu)系統(tǒng)參數(shù)；將參數(shù)代入模型后獲取系統(tǒng)的輸出信號，即為有效去噪的時變信號的恢復信號。本文以線性調(diào)頻信號為例研究說明了該模型對時變信號檢測和恢復的實用性和有效性，并最終得到理想的輸出信號，文章最后分析了不同時變信號的參數(shù)對系統(tǒng)輸出的影響并和傳統(tǒng)的隨機共振模型輸出做了對比分析。

2 雙穩(wěn)態(tài)隨機共振及其參數(shù)歸一化變換

在隨機共振的研究中，受微弱周期力與白噪聲驅動的非線性雙穩(wěn)系統(tǒng)實質(zhì)上描述的是一個質(zhì)點同時受到外力和噪聲驅動時，在一個對稱的雙穩(wěn)態(tài)勢阱中運動的模型，其動力學方程可以用經(jīng)典的朗之萬方程來描述[2]：

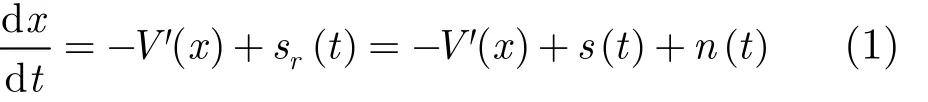
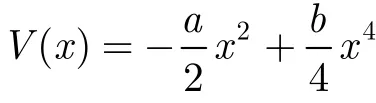
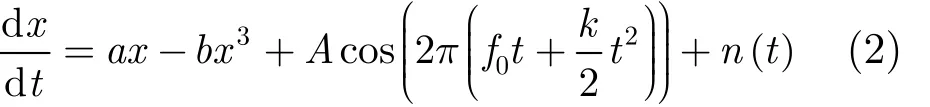
式中，A為LFM信號的幅值，f0為初始頻率，k為調(diào)頻率， f （ t） = f0+ k t則表示 LFM 信號的瞬時頻率； n （ t）=2Dξ（t）代表零均值的高斯白噪聲并且滿足 n （ t） n（ t + τ ） = 2 D δ （t ） （D 為噪聲密度）。從式（2）中可以看出，對稱雙勢阱的位置位于 xmin=±，勢壘高度 Δ V = a2/4b 。

為了在實際大參數(shù)下仍能利用絕熱近似理論得到SR現(xiàn)象，并識別微弱信號，文獻[18,19]分別提出了參數(shù)歸一化變換方法和二次采樣隨機共振來解決這一問題。但是文獻[18]提到當混合輸入信號的信噪比保持不變，對幅度進行縮放時，運用該方法在搜索合適的二次采樣頻率過程中可能會出現(xiàn)數(shù)值仿真發(fā)散的情況，所以這里采用歸一化變換方法。當雙穩(wěn)系統(tǒng)式（2）中的參數(shù)a, b取值不為1時，引入變換：

將式（3）代入式（2）中可得：

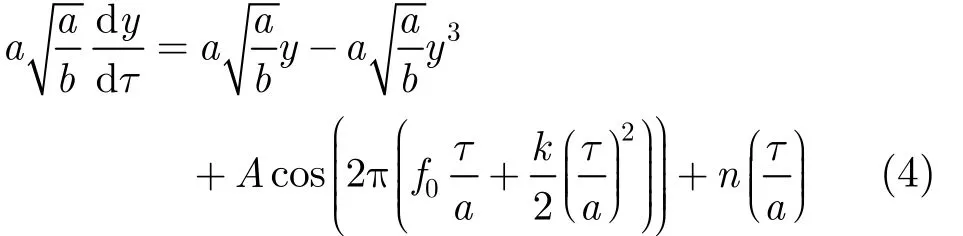
經(jīng)過變換后，式（4）中的噪聲信號為（）/naτ，而n（t）為白噪聲，頻域上均勻分布，因而（）/naτ仍然為零均值噪聲強度為D的白噪聲，簡化式（4）可以得到

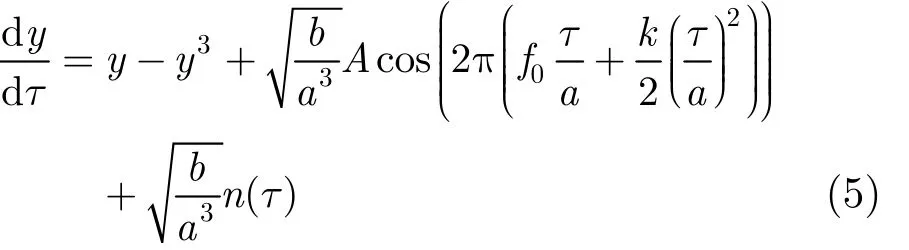
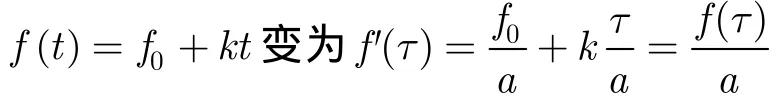
3 變參數(shù)隨機共振和輸出指標

實際上SR系統(tǒng)可以被當做是一個選通濾波器，傳統(tǒng)意義上的SR現(xiàn)象出現(xiàn)需要輸入信號中的微弱信號周期、系統(tǒng)噪聲強度和模型參數(shù)之間滿足一定的匹配條件，當兩勢阱間躍遷率rk=a/exp（-ΔV/D）的一半與周期信號頻率相匹配時，隨機共振現(xiàn)象就會出現(xiàn)。但是對于時變信號（非周期），這種匹配關系隨著時間變化不可能一直滿足。從文獻[18]中可知，對于第2節(jié)提到的參數(shù)歸一化變化過程中，參數(shù)a起著決定性作用，變換后的噪聲密度D' = a3D / b，增大為原來的a3/b倍，將ΔV和D'代入躍遷率 rk表達式可得：

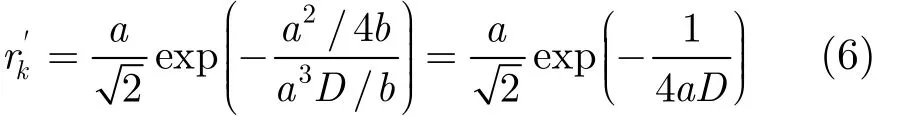
對于大參數(shù)信號，為了保證SR現(xiàn)象的出現(xiàn)，參數(shù)a往往會取很大的值，所以可以近似得到exp（- 1 /（4a D）≈ 1 。可以看出經(jīng)過歸一化變換后的SR系統(tǒng)的克萊姆斯躍遷率與參數(shù)a成正比。據(jù)此，本文提出一種用于檢測確知時變信號的變參數(shù)隨機共振系統(tǒng)，其參數(shù)a和輸入信號頻率保持相同的時變特點，表示為a（t），從另一角度看，此時變參數(shù)a（t）可以使得經(jīng)過歸一化變換后的信號對SR系統(tǒng)來說具有穩(wěn)定的頻率，以此來滿足SR現(xiàn)象發(fā)生的條件，對于如式（2）所示的系統(tǒng)，輸入信號為LFM信號時，所提出的模型可以表示為

其中，參數(shù) a （ t） = a0+ a0k t/f0，可以使歸一化變換后的信號等效頻率為

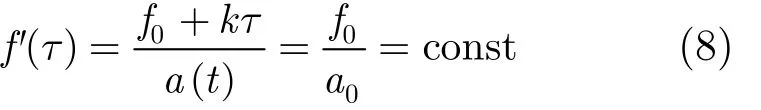
式中，const表示一固定的常量，所以在式（7）所示的模型下，輸入信號的等效驅動頻率將保持恒定，可以滿足與躍遷率匹配的條件，保證了SR現(xiàn)象的出現(xiàn)。同時，為了保證輸出信號幅值的穩(wěn)定性，必須使平衡位置xmin=保持恒定，取相應的參數(shù)b（ t） = b0+ b0k t/f0，同時將輸入信號隨時間變化放倍，求解式（7）得到結果即為VPSR輸出信號。

但是另一方面，由于時變信號的傅里葉變換頻譜上不會再出現(xiàn)單頻信號的能量集中的單一譜峰，傳統(tǒng)的SR系統(tǒng)中所使用的SNR作為衡量系統(tǒng)的標準將不再適用。對于非周期隨機共振的研究工作中，多數(shù)研究[13]都使用輸入信號中的純凈理想信號s（t）和經(jīng)SR系統(tǒng)后的輸出信號x（t）之間的時移最大互相關系數(shù)來表征，記作sxC ，對于離散化的信號，其表達式為

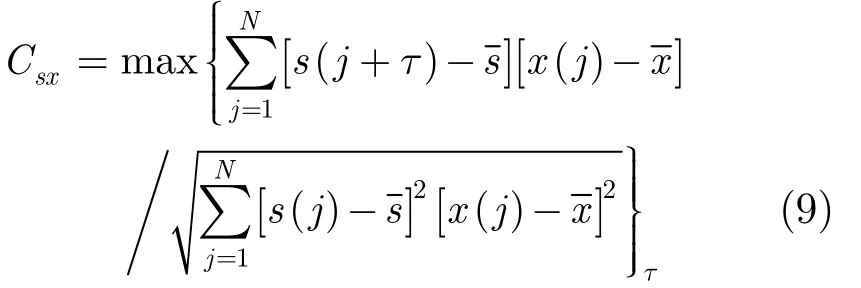
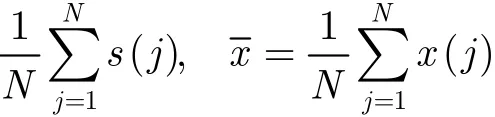
式中，殘差平方和（Sum of Squares for Error, SSE）表示實際值與擬合值的誤差平方和，總偏差平方和（Total Sum of Square, SST）表示實際值和平均值的誤差平方和。xi和x分別表示SR輸出信號及其平均值，?xi指輸出信號的擬合結果。很容易看出 R2≤ 1 恒成立而且其值越大表示原始數(shù)據(jù)與擬合數(shù)據(jù)越吻合，擬合誤差越小，也即輸出效果越好。

4 LFM信號的檢測和恢復結果

4.1 預定參數(shù)下的輸出

首先，本文根據(jù)前面模型提出和理論分析過程中所提到的LFM信號模型，利用Matlab數(shù)學工具進行線性調(diào)頻信號的數(shù)值仿真分析，并通過本文所提出的變參數(shù)隨機共振系統(tǒng)來進行信號的參數(shù)估計和去噪恢復。根據(jù)信號的理論公式 s（ t） = A c os（2π （f0t+k t2/2）+ φ ），建立一個仿真信號s（t），該LFM信號滿足：線調(diào)頻率k=5 kHz/s，初始頻率f0=1 kHz，初始相位 φ =-π / 2和信號幅值A=1，設定采樣頻率= 2 × 1 05Hz ，采樣時間T=0.15 s，得到理想信號如圖1（a）中的圓點虛線所示。利用Matlab的awgn函數(shù)向該信號中加入-5 dB的噪聲，可以獲得最終的混合輸入信號如圖1（a）的實線條所示，其左圖和右圖分～別為混合信號和理想LFM信號0～0.020 s和0.140 0.150 s時間段的放大細節(jié)視圖。

圖1 LFM仿真信號以及傳統(tǒng)SR和VPSR的輸出信號波形

本文分別利用預定參數(shù)的傳統(tǒng)SR系統(tǒng)和所提出的VPSR系統(tǒng)對信號進行去噪處理。對于傳統(tǒng)的SR模型，設定參數(shù)a=b=10000，同時將輸入信號放大= 1 0000倍，代入式（2）中，進行數(shù)值求解后，得到的輸出信號如圖1（b）實線所表示波形。使用Matlab的lsqcurvefit函數(shù)對輸出信號進行曲線擬合，圖1（b）中圓點虛線為擬合信號，且求得輸出信號與原信號相關系數(shù) Csx1= 0 .8193，擬合決定系數(shù)= 0 .5617。然后再利用所提出的VPSR模型，設定參數(shù)k=5 kHz/s, f0=1 kHz, a（ t） = b （ t） = a0+ a0kt/f0（a0= 1 0000），同時將輸入信號幅值隨時間放大10000倍，代入式（7）可以得到系統(tǒng)的輸出信號如圖1（c）實線所描繪。進行擬合后，圖1（c）中圓點虛線表示波形為擬合信號，同時求得輸出信號與原信號相關系數(shù) Csx2= 0 .9229，擬合決定系數(shù)= 0 .8243。與傳統(tǒng)隨機共振系統(tǒng)的輸出結果相比，可以看出，輸出信號的低頻段二者波形相差不大，都較為理想；但是到高頻段（圖1（b）和圖1（c）右圖），所提出的VPSR模型輸出波形更平整接近實際信號，而且可以從相關系數(shù)和擬合決定系數(shù)看出新模型的兩個參數(shù)也得到了明顯的提高。

4.2 最優(yōu)參數(shù)條件下的輸出

首先作為對比分析，本文利用最優(yōu)參數(shù)下傳統(tǒng)的雙穩(wěn)態(tài) SR模型對信號進行去噪處理。以系統(tǒng)輸出信號的擬合決定系數(shù)R2為參考指標，計算在不同系統(tǒng)參數(shù)a（b=a）條件下的輸出信號決定系數(shù)，得到的2

R a- 變化曲線。同樣利用4.1節(jié)中仿真的信號，可以得到如圖2（a）所示的曲線，從結果中可以看出，當取 a=23000時，系統(tǒng)輸出參數(shù)20.8357 R= 達到最大，此時系統(tǒng)對輸入信號達到最優(yōu)狀態(tài)。將參數(shù)和放大23000倍的輸入信號代入式（2），得到輸入信號的最有輸出結果如圖 2（b）中的實線所示，圓點虛線為對輸出信號按照線性調(diào)頻信號的擬合結果。

之后，利用VPSR模型對輸入信號進行處理。根據(jù)前面的描述，該模型（式（9））的參數(shù)有 a0=b0, f0和 k。所以需要對這 4個參數(shù)分別進行搜索，求得最優(yōu)值，然后代入系統(tǒng)。為了讓搜索過程可視化，本文給出了如圖3所示的幾個搜索結果。第1步，固定a0=b0=10000，然后對參數(shù)f0, k進行全局搜索，在搜索過程中，對每組參數(shù)?對應的輸出結果x（t）使 用 s '（t） = A 'c os（2π+/2）+ φ '） 進 行數(shù)據(jù)擬合，并將計算的擬合決定系數(shù) R2）作為輸出指標，可以得到系統(tǒng)參數(shù) f0, k的最優(yōu)組合 f0=1 kHz, k=5 kHz/s。圖 3（a）中，固定 f0=1 kHz，同時將k以0.1 kHz/s的增幅從3 kHz/s增加到7 kHz/s，得到輸出參數(shù)R2隨參數(shù)k的變化規(guī)律；同樣取k=5 kHz/s，將f0以10 Hz的增幅從0.8 kHz增加到1.2 kHz，得到R2隨參數(shù)f0的變化規(guī)律如圖3（b）所示。從兩幅圖中明顯可以看出，在f0=1 kHz, k=5 kHz/s時，R2達到一個峰值0.8243，所以得到這兩個參數(shù)的最優(yōu)組合，同時也對應著輸入信號的初始參數(shù)。

第2步，在獲得了輸入信號的參數(shù)之后，固定這兩個值，同時改變系統(tǒng)參數(shù) a0（b0=a0）。將 a0從5000開始以1000的間隔增加到50000，得到輸出參數(shù) R2隨 a0的變化關系如圖 3（c）所示，從結果中得到系統(tǒng)結構參數(shù)的最優(yōu)值 b0=a0=14000，此時輸出擬合決定系數(shù)R2=0.8721，相比于圖1和圖2中的結果都有了進一步的提升。將最優(yōu)參數(shù)組合代入式（7），得到最優(yōu)輸出如圖4所示。可以看出輸出信號中，原始信號中的噪聲經(jīng)過VPSR之后能量得到了有效轉移，輸出信號與理想的擬合結果已經(jīng)十分吻合。

本文將前面分析的結果綜合到表1中，其中包括最優(yōu)條件和非最優(yōu)條件下傳統(tǒng)隨機共振以及VPSR系統(tǒng)的相關參數(shù)和輸出結果，從表中可以看出所提出的系統(tǒng)對 LFM 信號具有更好的去噪和恢復效果，而且模型可以有效檢測出信號的固有參數(shù)，更好地用于后期信號的恢復工作。

5 模型輸出的性能分析

前面幾節(jié)以 LFM 信號為例詳細介紹了對噪聲背景下時變信號，利用本文所提出的模型進行信號檢測和恢復的過程。為了說明VPSR模型用于時變信號恢復的效果和優(yōu)勢，本文進一步研究分析了系統(tǒng)在不同輸入信號條件下的輸出結果，通過對比分析，具體揭示了輸入信號參數(shù)的不同對系統(tǒng)輸出的影響。

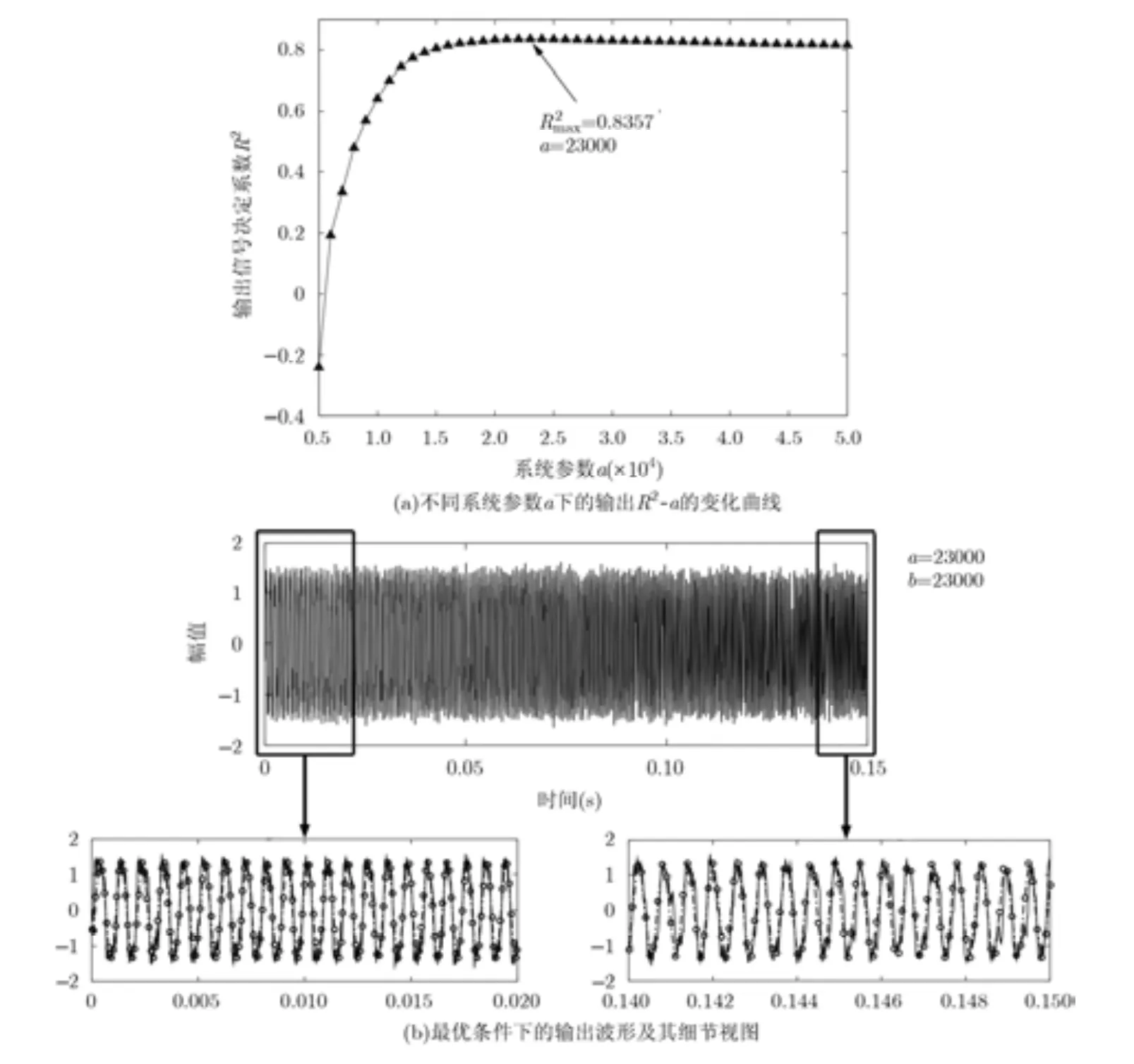
圖2 不同參數(shù)條件下傳統(tǒng)SR模型的輸出結果及最優(yōu)條件下的系統(tǒng)輸出

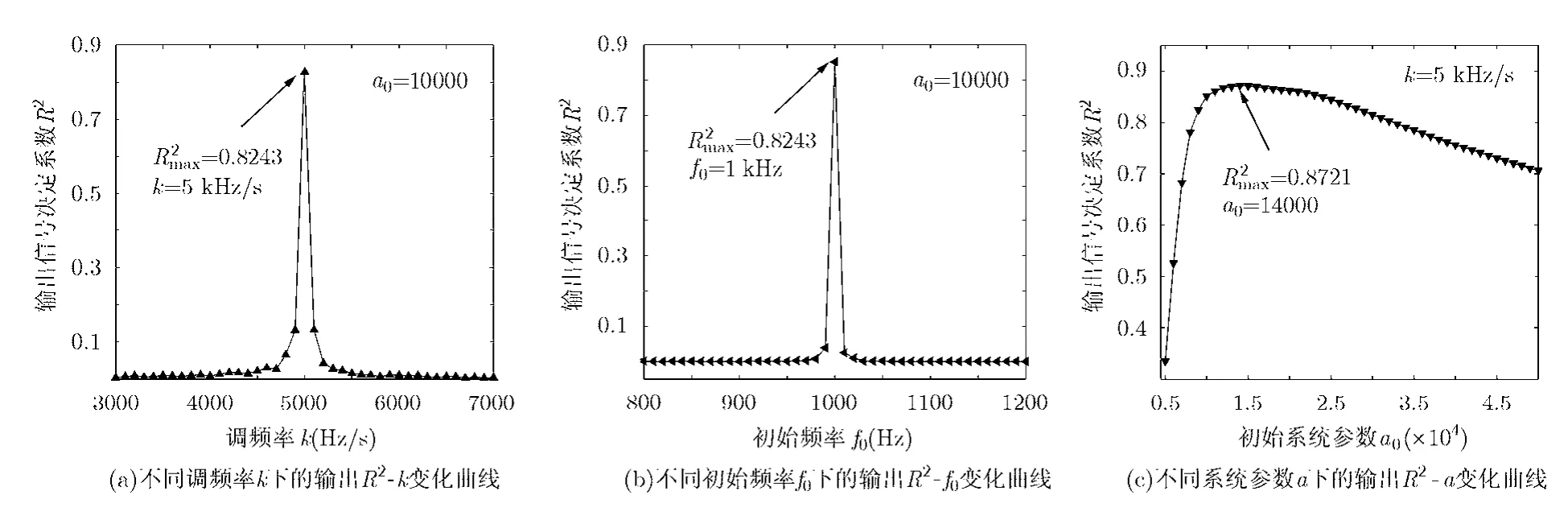
圖3 VPSR模型下不同參數(shù)變化對輸出結果的影響

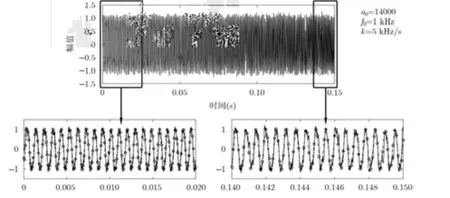
圖4 最優(yōu)參數(shù)條件下VPSR模型的輸出波形及其細節(jié)視圖

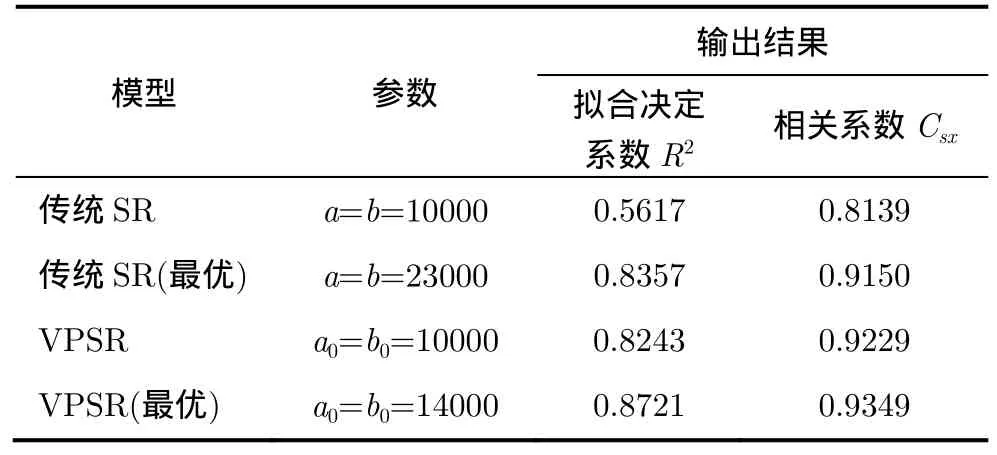
表1 不同參數(shù)下兩種模型的輸出比較

5.1 調(diào)頻率k的影響

首先，固定初始頻率f0=1 kHz，輸入信噪比SNR=-5 dB，保持采樣頻率和前面的仿真信號一樣 fs=200 kHz，初始相位 φ =-π / 2和信號幅值A=1，采樣時間T=0.15 s，同時，將k以200 Hz/s的間隔從4 kHz/s增加到20 kHz/s。對于每個k值，獲取最優(yōu)系統(tǒng)參數(shù)并得到輸出信號的決定系數(shù)R2和相關系數(shù)Csx，結果如圖 5 所示，圖 5（a）和圖 5（b）分別表示輸出信號的決定系數(shù)和相關系數(shù)，圖中三角點表示VPSR模型中不同 k值對應的輸出結果，圓點表示傳統(tǒng)SR模型的輸出結果，星點表示原始信號的相關參數(shù)。

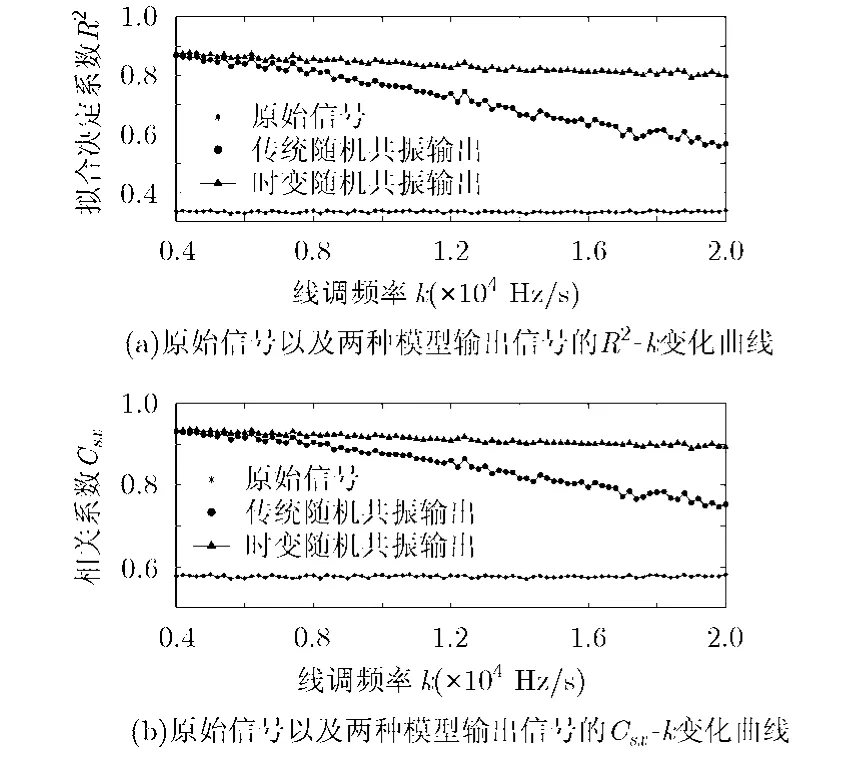
圖5 線調(diào)頻率對不同模型輸出結果的影響

圖 5（a）和圖 5（b）中，不同模型下輸出參數(shù)都隨著 k的增加而降低，但是本文所提出的模型輸出參數(shù)下降的速率比傳統(tǒng)的SR模型要低得多，其降低的趨勢并不明顯，而傳統(tǒng)的SR模型的輸出參數(shù)下降迅速，這就說明k值越大，本文所提出的VPSR模型優(yōu)勢越明顯。

5.2 初始頻率f0的影響

選取調(diào)頻率k=10 kHz/s，將初始頻率f0從0.5 kHz到2.5 kHz之間每隔50 Hz取一個點，信號其他參數(shù)保持和5.1節(jié)一致。同樣，對每一個f0，搜索最優(yōu)的系統(tǒng)參數(shù)并得到輸出信號的決定系數(shù)R2和相關系數(shù)Csx。圖6為不同的初始頻率對應的輸出參數(shù)，可以看出，兩種模型的輸出信號和輸入信號相比都能有效地提高輸出參數(shù)，抑制噪聲，恢復原始信號。但是還可以發(fā)現(xiàn)，在初始頻率較大時，VPSR和傳統(tǒng)的 SR模型相比優(yōu)勢并不明顯，輸出參數(shù)相差無幾，但是在初始頻率較小時，兩種模型輸出結果相差很明顯，而且初始頻率越小，VPSR的輸出參數(shù)出現(xiàn)上升的趨勢，但是傳統(tǒng)SR卻逐漸下降，VPSR模型的優(yōu)勢也越來越明顯。

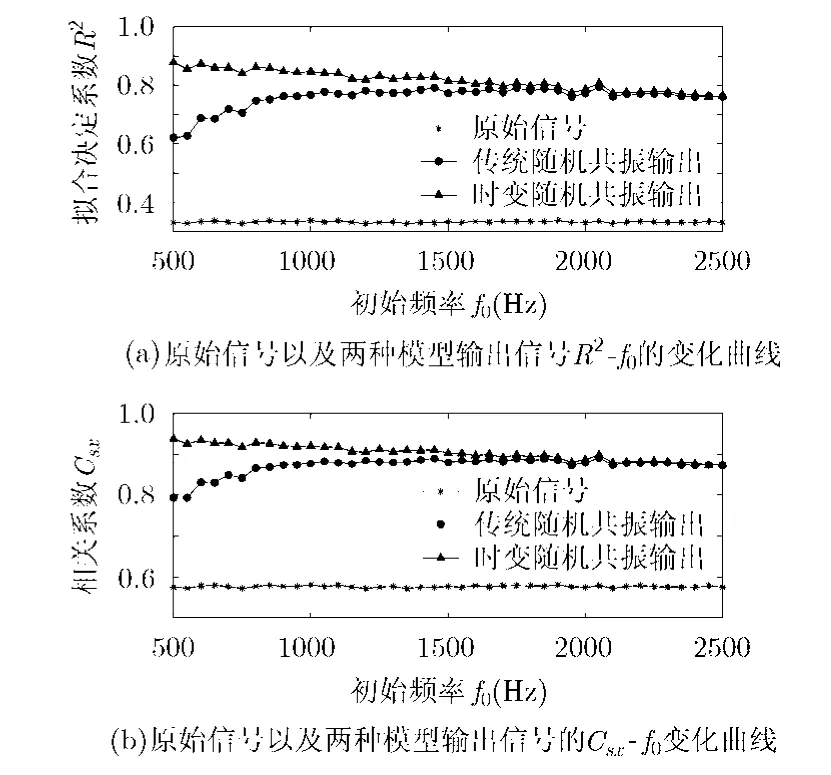
圖6 初始頻率對不同模型輸出結果的影響

通過上面研究表明，本文所提出的VPSR模型能夠在LFM信號（時變信號）的去噪處理中有著更好的效果并且提供更為理想的恢復信號，特別是在低初始頻率、高調(diào)頻率（對應其他時變信號的頻率變化率）的輸入信號時，該模型更有效，對于頻率帶寬較寬的信號具有更強的適應性。

6 結束語

論文針對已知時變特性的時變信號（以 LFM 信號為例），提出了一種基于變參數(shù)的隨機共振系統(tǒng)（VPSR），用于檢測時變信號固有參數(shù)和恢復強噪聲背景下的信號。該模型通過以輸出信號的決定系數(shù)為標準，通過搜索估計輸入信號的固有參數(shù)（k和f0），確定固有參數(shù)后，再利用相同的指標搜索決定模型的最優(yōu)系統(tǒng)參數(shù)，最后通過兩組參數(shù)得到輸入信號的最優(yōu)輸出結果，即為本文所需要的去噪后的理想信號。通過仿真分析，可以看出所提出的模型能夠獲取更滿意的輸出結果，同時也具有諸多的優(yōu)勢。（1）該模型結合了參數(shù)歸一化方法，有效解決了隨機共振系統(tǒng)中由于絕熱近似條件所帶來的小參數(shù)限制；（2）本文提出的模型通過引入時變系統(tǒng)參數(shù)（a（t）和 b（t）），能夠一樣很好地處理時變信號，這為對處理一些其他的像多普勒信號等非線性時變信號提供了新的方向和思路；（3）仿真結果顯示，該方法在處理一些頻率變化率較大、初始頻率較小的時變信號時優(yōu)勢明顯，也就是對于一些頻率隨時間變化較快、頻率范圍較寬的信號，利用傳統(tǒng)的SR系統(tǒng)就無法有效恢復出理想信號，這時本文所提出的模型仍然具有更好的適應性和有效性。

所以，VPSR能夠在時變信號的檢測和恢復中有著很好的表現(xiàn)，具有一定的指導意義和實用價值。但是盡管具有很多優(yōu)點，但是目前該系統(tǒng)需要知道待處理信號的頻率變化規(guī)律，下一步的工作也將集中在處理一些未知規(guī)律的時變信號處理，發(fā)展自適應地時變隨機共振系統(tǒng)，并且將模型有效利用到實際信號和工程應用中。

[1] Benzi R, Sutera A, and Vulpiani A. The mechanism of stochastic resonance[J]. Journal of Physics A: Mathematical and General, 1981, 14（11）: L453-L457.

[2] Gammaitoni L, Hanggi P, Jung P, et al.. Stochastic resonance[J]. Reviews of Modern Physics, 1998, 70（1）:223-287.

[3] 鄭仕譜. 基于隨機共振的弱信號提取方法研究[D]. [碩士論文],浙江大學, 2014.Zheng Shi-pu. Study on weak signal extraction technology using stochastic resonance[D]. [Master dissertation], Zhejiang University, 2014.

[4] 楊祥龍, 汪樂宇. 一種強噪聲背景下弱信號檢測的非線性方法[J]. 電子與信息學報, 2002, 24（6）: 811-815.Yang Xiang-long and Wang Le-yu. A new detection method of weak signal in strong background-noise level[J]. Journal of Electronics & Information Technology, 2002, 24（6）: 811-815.

[5] 梁軍利, 楊樹元, 唐志峰. 基于隨機共振的微弱信號檢測[J].電子與信息學報, 2006, 28（6）: 1068-1072.Liang Jun-li, Yang Shu-yuan, and Tang Zhi-feng. Weak signal detection based on stochastic resonance[J]. Journal of Electronics & Information Technology, 2006, 28（6）:1068-1072.

[6] 王強. 基于變步長隨機共振的弱信號檢測技術[J]. 信息通信,2014, 12（8）: 25.Wang Qiang. Weak signal detection based on step-change stochastic resonance[J]. Information & Communications, 2014,12（8）: 25.

[7] Li Ji-meng, Chen Xue-feng, and He Zheng-jia. Multi-stable stochastic resonance and its application research on mechanical fault diagnosis[J]. Journal of Sound and Vibration,2013, 332（22）: 5999-6015.

[8] 冷永剛, 田祥友. 一階線性系統(tǒng)隨機共振在轉子軸故障診斷中的應用研究[J]. 振動與沖擊, 2014, 62（17）: 1-5.Leng Yong-gang and Tian Xiang-you. Application of a first-order linear system's stochastic resonance in fault diagnosis of rotor shaft[J]. Journal of Vibration and Shock,2014, 62（17）: 1-5.

[9] Lu Si-liang, He Qing-bo, and Kong Fan-rang. Stochastic resonance with Woods-Saxon potential for rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2014, 45（2）: 488-503.

[10] Xu Jia-wen, Shao Wei-wei, Kong Fan-rang, et al.. Right-angle piezoelectric cantilever with improved energy harvesting efficiency[J]. Applied Physics Letters, 2010, 96（15）:152904（1-3）.

[11] Harne R L and Wang K W. A review of the recent research on vibration energy harvesting via bistable systems[J]. Smart Materials and Structures, 2013, 22（2）: 023001（1-12）.

[12] 朱文濤, 蘇濤, 楊濤, 等. 線性調(diào)頻連續(xù)波信號檢測與參數(shù)估計算法[J]. 電子與信息學報, 2014, 36（3）: 552-558.Zhu Wen-tao, Su Tao, Yang Tao, et al.. Detection and parameter estimation of linear frequency modulation continuous wave signal[J]. Journal of Electronics &Information Technology, 2014, 36（3）: 552-558.

[13] 朱健東, 趙擁軍, 唐江. 線性調(diào)頻連續(xù)波信號的周期分數(shù)階Fourier變換檢測與估計[J]. 電子與信息學報, 2013, 35（8）:1827-1833.Zhu Jian-dong, Zhao Yong-jun, and Tang Jiang. Periodic FRFT based detection and estimation for LFMCW signal[J].Journal of Electronics & Information Technology, 2013, 35（8）:1827-1833.

[14] Collins J J, Chow C C, Capela A C, et al.. Aperiodic stochastic resonance[J]. Physical Review E, 1996, 54（5）:5575-5584.

[15] 段江海, 宋愛國. 雙穩(wěn)系統(tǒng)中非周期隨機共振的數(shù)值仿真[J].電路與系統(tǒng)學報, 2004, 9（5）: 149-152.Duan Jiang-hai and Song Ai-guo. Numerical simulations of aperiodic stochastic resonance in bistable systems[J]. Journal of Circuits and Systems, 2004, 9（5）: 149-152.

[16] Wang Xiao-min and Wen Chuan. Detection and parameter estimation of LFM signal based on stochastic resonance[C].Proceedings of the 2011 2nd International Conference on Networking and Information Technology, Singapore, 2011,112-119.

[17] Peng Hao, Zhong Su-chuan, Tu Zhe, et al.. Stochastic resonance of over-damped bistable system driven by chirp signal and Gaussian white noise[J]. Acta Physica Sinica, 2013,62（8）: 080501（1-6）.

[18] Yang Ding-xin, Hu Zheng, and Yang Yong-min. The analysis of stochastic resonance of periodic signal with large parameters[J]. Acta Physica Sinica, 2012, 61（8）:080501（1-10）.

[19] Leng Yong-gang, Wang Tai-yong, Qin Xu-da, et al.. Power spectrum research of twice sampling stochastic resonance response in a bistable system[J]. Acta Physica Sinica, 2004,53（3）: 717-723.