DDAG支持向量機在ERT系統流型識別中的應用

張華

（吉林建筑大學城建學院，長春 130011）

兩相流是一種廣泛存在于自然界和工業生產過程中的混合流動模式，特別在化工、石油、電力、核能及冶金等行業普遍存在。近年來，兩相流的研究逐步發展成為國際上研究的熱點，其主要原因在于兩相流不僅在一系列現代工程中得到廣泛應用，而且對促進這些設備的發展和創新也起到了重要作用。因此兩相流的參數測量和流型識別具有重要的理論和工程意義［1］。小波包分析是在小波分析基礎上發展起來的更加精密的時頻分析方法，它在信號去噪、濾波、壓縮、非平穩機械振動信號的分析與故障診斷、非平穩信號的特征提取等方面具有重要應用。支持向量機是統計學習理論中最年輕實用的內容，是為適用于小樣本學習而提出的通用學習算法。本文以ERT系統和油/水兩相流的流型為研究基礎，首先采用小波包分析對ERT系統測量的壓差波動信號進行特征提取，然后通過計算類間不可分離程度為每個節點選取最易分的兩類構造DDAG支持向量機多類分模型，最后將提取的特征數據輸入構造好的分類模型進行流型識別。

1 ERT系統組成結構及工作原理

電阻層析成像系統主要由電阻傳感器陣列、數據采集系統、圖像重建計算機三部分組成［2］。系統結構如圖1所示。ERT系統的工作原理通常是電流激勵、電壓測量。本文是基于12電極ERT系統采集的到電導率波動信號進行處理，由于采用相鄰的激勵模式，所以一幅圖像共采集到N（N-3）個測量數據，即12×9=108個。系統工作原理圖如圖2所示。

圖1 電阻層析成像系統結構圖

圖2 系統工作原理圖

2 小波包分析原理及特征提取過程

2.1 小波包分析原理及算法

小波包分析是對非平穩信號進行特征提取的較好工具，它能夠為信號提供一種更加精密的分解方法。它在小波分析的基礎上將頻帶進行多層次劃分，對多分辨率分析沒有細分的高頻部分進一步分解，并能夠根據被分析信號的特征，自適應地選擇相應的頻帶，使之與信號頻譜相匹配，進一步提高時頻分辨率［3］。

2.2 小波包特征提取步驟

（1）對輸入信號S，采用db6小波濾波器，shanon熵值進行三層小波包分解，從第三層中提取低頻到高頻8個頻率成分的信號特征［4］。

（3）利用公式

其中E滿足公式：

對所求得能量值做歸一化處理。

（4）用各頻段能量作為特征值，構造特征向量，即

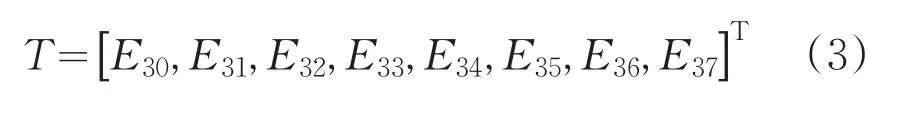
3 支持向量機原理及建立多類分類模型

3.1 支持向量機原理

支持向量機是為適用于小樣本學習而提出的通用學習算法。它根據VC（Vapnik-Chervonenkis）理論［5］，基于結構風險最小化原理，從而能兼顧訓練錯誤和泛化性能，開辟了機器學習算法的新天地。目前這種新的學習算法被建議用以代替多種傳統的神經網絡方法，已經成為機器學習研究的熱點，并在很多領域得到了成功的應用。

由支持向量機定義，構造非線性最優超平面的問題轉化為一個較簡單的二次規劃：

訓練完成后，計算下列函數的符號即可：

3.2 建立DDAG多類分類模型

支持向量機最初是針對二類分類問題提出的，上述支持向量機原理只能解決兩個類別的分類問題。而實際應用中常常是多個類別的分類問題［6］。常見的多類分類策略有一對一、一對多和DDAG［7］，前兩種方法存在不可分區域。傳統的DDAGSVM在訓練階段構造K（K-1）/2個兩類分類器，在分類階段，將K（K-1）/2個兩類分類器構造成一個二叉樹有向無環圖。對待分類樣本X，從樹型拓撲結構根節點開始，根據支持向量機決策函數的值決定走左節點或者是右節點。以此類推，直到達到葉結點，此葉節點的類別就是待分類樣本X的類別。但是DDAG模型存在誤差累積的問題［8］，即當根節點產生分類錯誤時將會直接影響下層各節點的分類結果。解決誤差累積問題的一般方法是用馬氏距離或類中心間距離作為類間分離程度的度量，但是這兩種方法沒有考慮樣本空間分布的幾何狀況。要想正確的進行類間分離程度度量還需要考慮樣本在空間的類內分散度［9］。

首先，第i類和第 j類樣本的中心距離用

其次，第i類樣本的類內分散度表示為：

由以上兩類樣本中心距離和兩類類內分散度，得到兩類間不可分程度計算公式：

對ERT系統中的四種流型：點滴流、核心流、層流、環狀流進行識別，采用改進的DDAG方法構造支持向量機多類分類模型。根據流型個數4，需要構造4*（4-1）/2=6個SVM兩類分類器，如圖3所示。步驟如下（以判別1類為例）：

第一步：設給定的訓練集為{(x1,y1),(x2,y2),...,(xl,yl)}，l代表用l組樣本數據進行訓練。

其中 xi∈Rn，yi∈{1,2,3,4}，i=1,2,...,l。

第二步：根據以上得到的兩類間不可分離程度公式計算每兩種流型的不可分離值。選擇最小的值（可分離性最高）所對應的兩種流型（假設為1和2）作為樹型拓撲結構根節點支持向量機要區分的兩類。

第四步：在某個節點的剩余類別中，重復第二步和第三步，直到達到葉子節點，此節點所對應的類別就是待分樣本X所屬的類別。

圖3 DDAGSVM多類分類模型

3.3 實驗過程和識別結果分析

本實驗采用MATLAB編程，在小波包工具箱和LS支持向量機工具箱基礎上修改得到。首先為每種流型隨機選取30個樣本進行訓練。由ERT系統工作原理可知每種流型由108個數據表示，經過小波包分解變為8維數據，將特征提取后的數據輸入DDAG支持向量機多類分類模型。在本實驗中，支持向量機采用最小二乘支持向量機算法［10］，對訓練結果影響不大的核函數隨機選擇徑向基核函數。對訓練結果影響較大的兩個參數，一是控制對錯分樣本懲罰程度的可調參數gam，二是徑向基核函數的參數sig2，它們的選取采用代價較小的網格搜索法，即多次調整兩個參數的范圍和采樣間隔，找到最優的組合。訓練完成后，再為每種流型隨機選取30個樣本進行測試。通過與以往基于其他策略的支持向量機多類分類模型比較，可得出DDAG支持向量機多類分類模型在ERT系統流型識別中具有較高的識別精度。實驗結果統計分析如表1所示。

表1 實驗結果統計分析

4 結論

本文提出在ERT系統流型識別中采用小波包和改進的DDAG支持向量機多類分類模型相結合方法進行識別。實驗結果證明在特征提取方式一樣的情況下，改進的DDAG支持向量機多類分類模型在識別樣本時相比于其他多類分類模型的識別準確率都要高，說明此種方法適用于兩相流流型識別的領域。

［1］王金龍，孫福龍，杜新.質子交換膜燃料電池陰極氣液兩相流模型的建模及仿真［J］.長春理工大學學報：自然科學版，2014，37（3）：83-86.

［2］Dickin F J，Wang M.Electrical resistance tomography for process application［J］.Measurement Science and Technology，1996，7（3）：247-260.

［3］Elperin T，Klochko M.Flow regime identification in a two-phase flow using wavelet transform［J］.Springer-Verlag，2002（32）：674-682.

［4］周明月，杜麗敏，姜文龍.基于高階統計量的小波變換去噪算法［J］.長春理工大學學報：自然科學版，2009，32（2）：251-253.

［5］張學工.關于統計學習理論與支持向量機［J］.自動化學報，2000，26（1）：32-42.

［6］Qi Guohua，Dong Feng，Xu Yanbin，et al.Gas/Liquid two-phase flow regime identification in horizontal pipe using support vector machines［A］.Proceedings of the Fourth International Conference on Machine Learing and Cybernetics，2005：1746-1751.

［7］余輝，趙輝.支持向量機多類分類算法新研究［J］.計算機工程與應用，2008，44（7）：185-189.

［8］趙亮.一種改進的基于支持向量機的多類分類方法［J］.計算機應用與軟件，2014，31（12）：233-236.

［9］熊忠陽，陳玲，張玉芳.一種改進的DDAGSVM多類分類方法［J］.計算機系統應用，2010，19（12）：219-222.

［10］Peng Zhenrui，Mi Gensuo.Voidage measurement of two-phase flow based on least squares support vectormachine［A］.Proceedingofthe 6thWorld Congress on Intelligent Control and Automation，2006：4900-4903.