基于EDC模型的含HCN 火災煙氣數值模擬及毒性評價

陳 銀，蔣 勇，潘龍葦，葉美娟

（中國科學技術大學火災科學國家重點實驗室，安徽 合肥 230027）

火災產生的煙氣具有強烈的毒害作用，會對人的生命構成巨大威脅。統計表明，火災中80%以上的遇難者都是吸入了有毒氣體昏迷后致死的，大約有2／3的煙氣中毒遇難者的死亡地點是在離起火點很遠處的走廊或者房間［1-2］。隨著材料多樣性的發展，聚氨酯等高分子材料在建筑裝修材料中的使用越來越廣泛，現代材料熱解和燃燒的毒性產物也有所變化［3-7］。比如，聚氨酯燃燒會產生大量氰化氫（HCN）氣 體，而HCN 的毒性 比CO 高 出20 多倍［8］。傳統的火災煙氣毒性研究大多針對CO［9］，然而大量實驗證明毒性氣體產物耦合作用的結果是造成火災煙氣毒效性和致死性的主要原因。美國國家標準技術研究所（NIST）提出了N-GAS 模型煙氣毒性評價方法［10］，認為煙氣毒性緣于部分主要的毒害氣體。但由于全尺度火災試驗和數值模擬中測量毒性氣體產物產量的手段存在嚴重的局限性，且對這些毒性產物的性質和特點缺乏足夠認識［11］，導致N-GAS模型的實際運用并不廣泛。

從理論上來說，要測量燃燒產物中復雜毒性氣體的產量須使用燃料燃燒的詳細化學反應機理，但是在一個全尺度的火災場景中應用反應機理，以現有的計算資源難以滿足其計算量的需求。因此，本文從計算量和實用性兩個角度出發，在大渦模擬中嵌入可以耦合多步化學反應的EDC模型［12-17］，實現火災過程中利用EDC 模型獲取毒性氣體產量的方法；同時，以某沙發作坊為例，采用EDC模型耦合聚氨酯燃燒的化學反應方程式進行火災場景數值重構，獲得毒性氣體產物的分布和發展場圖，并在NGAS模型的基礎上評價煙氣毒性，研究HCN 對火災煙氣毒性的影響。

1 火災煙氣數值模型

湍流流動模型的基礎是質量、動量和能量的納維斯托克斯（N-S）方程［18］。采用大渦數值模擬（LES）方法將湍流中的大渦漩通過N-S方程直接求解，小渦旋通過亞網格尺度模型建立與大尺度渦旋的關系對其進行模擬［18］。為了解決復雜化學反應的常微分方程，采用的數值方法是一個以二階Runge-Kutta法為基礎并利用Richardson 外推法控制誤差、提高精確度的四階顯式積分方法。

1.1 渦耗散概念（EDC）模型

湍流渦耗散概念（EDC）模型是Magnussen在渦耗散模型的基礎上提出的，該模型假定湍流由一系列不同尺度的渦旋構成，湍動能從較大尺度的渦旋向小尺度湍流結構傳遞［11-13］。湍流的渦旋從主流到細微被分為不同級別結構，其中細微結構是渦旋尺度級別最小的湍流結構。湍動能耗散僅發生在可由Kolmogorov尺度刻畫的小尺度湍流結構中，大約3／4的耗散發生于細微結構中，并將所有的湍動能耗散成了熱［11-13］，因而耗散區又稱為細微結構區。

EDC模型認為各個組分均勻分布于細微結構中，反應物在其中進行分子級的混合，當達到所需的反應溫度時就發生相應的化學反應。引入湍動能和耗散率，細微結構中反應物所占比例γ可表達為

式中：CD1和CD2均為常數，CD1=0.134，CD2=0.5；υ為耗散區運動粘度（m2／s）；ε 為湍動能耗散率（m2／s3）；k為湍動能（m2／s2）。

細微結構和周圍流體間的質量傳遞速率m＊（s-1）為

式中：ρ為反應物密度（kg／m3）；Yi為組分i 在細微結構區的初始質量分數（kg／kg）；Y＊i為組分i 在反應發生τ＊時后的質量分數（kg／kg）。

超出時間尺度τ＊的化學反應速率按照Arrhenius公式計算。

1.2 N-GAS模型

美國NIST提出了N-GAS模型煙氣毒性評價方法，假設煙氣毒性緣于部分主要的毒害氣體（NGAS），每種氣體的毒性由動物試驗的結果來確定，同時考慮不同氣體成分間的拮抗和協同作用［9］。其評價方法如下：首先測量燃燒所釋放出的各個組分的濃度；然后把測量結果轉換成各個組分對動物致死量在總劑量中所占的比例［8］；最后求和得到煙氣的部分有效暴露劑量FED，即

式中：FED 為煙氣的部分有效暴露劑量；Ci為第i種氣體的濃度（ppm，1 ppm=10-6）；t 為時間（min）；LCt50（i）為第i種氣體的半致死濃度與暴露時間的乘積（ppm·min）。

在很多實際情況下，暴露時間是固定的，則FED 的計算公式如下：

式中：［Xi］表示Xi氣體的濃度（ppm）；LC50（Xi）表示Xi氣體的半致死濃度（ppm）；m、b為與CO、CO2有關的常數，當［CO2］≤5%時，m=-18，b=122 000，當［CO2］＞5%時，m=23，b=-38 600；暴露時間為30 min時，LC50（O2）為5.4%，LC50（HCN）為150ppm。

理想情況下，當FED=1.0時50%的動物會死亡；但由于公式的非線性，實際上50%動物致死率發生在FED=1.1時。表1為美國NIST 的動物實驗結果與N-GAS模型預測結果的對比。表1的左邊是僅含CO、CO2和O23種氣體的煙氣致死情況和相應的FED 的預測值；右邊是含CO、CO2、O2和HCN 4種氣體的煙氣致死情況和相應的FED 的預測值。

表1 動物實驗與N-GAS模型預測結果的對比Table 1 Comparison of predicted results of N-GAS Model and mortalities in animal tests

2 模型設置

2.1 火災概況

2006年云南省昆明市某沙發作坊發生火災，造成10人死亡、2人受傷以及大量經濟損失。該小型加工廠建筑高3層，磚混結構，長16m、寬16m，3層總高度為9.6 m，每層樓高3.2 m。建筑每層地（底）面平面圖和死亡人員的位置如圖1所示。

圖1 建筑結構平面圖和死亡人員位置Fig.1 Architecture structure plan and dead locations of persons

2.2 火災場景設置

火災場景設置如圖2所示。起火物質主要為一樓堆積的海綿，火源面積為0.8m×0.8m，熱釋放速率為500kW／m2，在1～4 號死亡人員位置設置相應的監測點，4個監測點均遠離火源位置。

圖2 火災場景設置示意圖Fig.2 Sketch map of fire scenario

為了驗證EDC模型引入的正確性，將新修改的模型與已受到普遍認可的CFD軟件模擬計算的結果進行對比，且后者無法計算HCN 產量。將未嵌入EDC模型、煙氣成分不包含HCN 的模擬設置編號為A 組；在大渦模擬中嵌入EDC 模型、煙氣成分包括HCN的模擬設置編號為B組。A 組相應的監測點標號為A1～A4，B組相應的監測點標號為B1～B4。

3 模擬結果與分析

3.1 模擬數據驗證

火災對人員的傷害主要來自高溫和毒性。圖3為A、B兩組1～4號監測點溫度T 隨時間t的變化曲線。由圖3可見，兩組數值模擬計算結果一致性良好，最高溫度均不超過180℃，但4號監測點溫度較低，最高溫度不超過100 ℃。

圖3 A、B兩組各監測點溫度隨時間的變化曲線Fig.3 Variation curves of temperature at monitoring points of group A and group B

人體在高溫環境中所能忍耐的最長時間隨溫度的升高而減小，考慮空氣濕度的影響，高溫環境下人體極限忍耐時間和溫度之間的關系（Crane公式）［20］可表示為

式中：t為人體極限忍耐時間（s）；T 為空氣溫度（℃）。

根據Crane公式，在180℃的高溫環境下，人體可以承受的時長約為142s；在150℃的高溫環境下，人體可以承受的時長約為274s；在100 ℃的高溫環境下，人體可以承受的時長約為1 200s。因此，可以認定此次沙發作坊火災致死的最主要原因并非高溫燒死或燙死。

火災過程中會產生大量的一氧化碳（CO）氣體，是常見的火災煙氣成分。CO 是一種無色無味的氣體，進入人體后會與血紅蛋白結合從而使人體缺氧，造成組織窒息［21-23］。

圖4為A、B兩組1～4號監測點CO濃度隨時間的變化曲線。由圖4可見，二樓樓梯口（2號監測點）CO濃度較低，而3號和4號監測點CO 濃度相對較高，可能是樓道口發生了強烈的煙囪效應的緣故。

圖4 A、B兩組各監測點CO 濃度隨時間的變化曲線Fig.4 Variation curves of CO concentration at monitoring points of group A and group B

圖5為火勢最大時（540s左右）建筑每層層高1.5m 處CO 濃度的時空分布圖。由圖5 可見，一樓東南角房間CO 濃度遠低于其他房間，這是因為此處是主要的空氣入口處；而劇烈的煙囪效應使得三樓的CO 濃度迅速升高。

上述數據顯示兩組的溫度隨時間的變化曲線、火災煙氣中CO 濃度的時空分布都是吻合的，也就是說應用EDC模型耦合多步化學反應方程式的數值模擬計算結果是十分理想的。

圖5 火災中建筑每層層高1.5m 處CO 濃度的時空分布圖（單位為×103 ppm）Fig.5 Comparison of CO concentration field patterns of 1.5mhigh in every floor in group A and group B

經過對比，新模型在計算量能夠接受的情況下，既保證了全尺度火災場景模擬計算結果的可靠性，又可以在計算過程中耦合多步化學反應，捕集火災過程中主要毒性氣體的產量，從而促進了N-GAS模型等煙氣毒性評價方法在實際中的運用。

3.2 CO 濃度分布

圖6 火災中建筑每層層高1.5m 處的CO 濃度等值線（單位為ppm）Fig.6 Contour lines of CO concentration of 1.5m high in every floor in group A and group B

為了評價利用EDC 模型獲得的多組分煙氣毒性，必須獲得每一種煙氣組分的濃度分布，其中CO和HCN是主要毒性物質。圖6為火災發展中期（350s左右）到火災猛烈時期（540s左右）建筑每層層高1.5m 處CO 的時均濃度等值線。根據毒理學的研究分析，當人體暴露在CO 濃度為1 000ppm的環境中1h時會出現頭痛、頭昏、惡心等癥狀，超過2h會引起死亡；當CO 濃度為2 000ppm 時1h后人會有危險或引起死亡；當CO 濃度為5 000ppm時20～30 min 人會窒息死亡；當CO 濃度達到11 000～12 000ppm 時人會在1～2min內停止呼吸［23］。由圖6可見，建筑一樓CO 最高濃度為1 943 ppm，在火源位置；二樓和三樓CO 最高濃度均低于1 000ppm。實際火災調查顯示，火災發生和發展的時間少于1h，也就是說，火災事故人員死亡原因不僅僅是CO 的毒效性。

3.3 HCN 濃度分布

HCN 是火災產物中一種具有急性作用的劇毒氣體，可以抑制人體內呼吸酶的功能使組織無法從血液中獲得氧氣，產生窒息作用［24-25］。當人體暴露在HCN 濃度為20～50ppm 的環境中2～4h后會產生暈眩、頭痛、惡心、嘔吐等癥狀；當HCN 濃度為100～200ppm 時人會在30～60 min 內死亡；當HCN 濃度達到300ppm 左右時人會立即死亡，而CO 的即刻死亡濃度超過了10 000ppm［23］。圖7為沙發作坊火災1～4號死亡位置HCN 濃度隨時間的變化曲線。由圖7可見，4個監測點的HCN 濃度均在300～400s之間達到即刻死亡濃度。

圖7 火災中1～4號死亡位置HCN濃度隨時間的變化曲線Fig.7 Variation curves of HCN concentration at the 1to 4dead locations with time

火災過程中建筑每層樓層高1.5m 處的HCN濃度的時均等值線見圖8，時間為350～540s之間。由圖8可見，除了死亡位置，室內其他區域的HCN濃度也都超過了即刻致死濃度；除了火源位置和樓梯口，毒性氣體在建筑物各個墻角堆積較多。

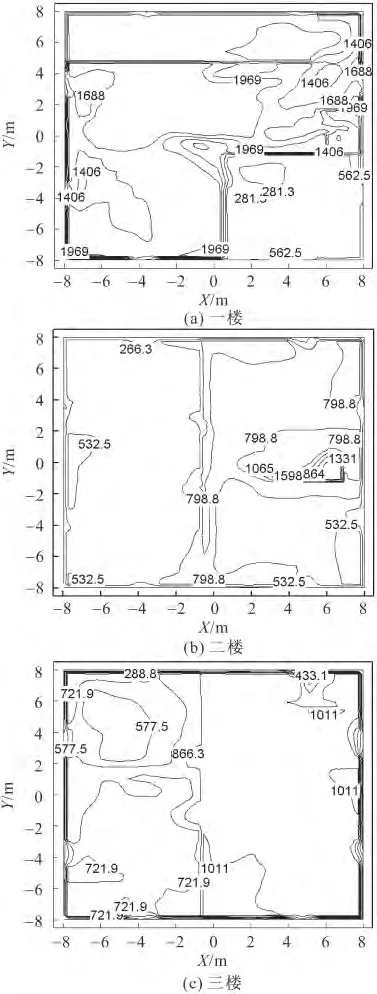
圖8 火災中建筑每層層高1.5m 處的HCN 濃度等值線（單位為ppm）Fig.8 Contour lines of HCN concentration of 1.5mhigh in each floor

3.4 火災煙氣毒性評價

毒性產物的有效捕集和計算使得N-GAS模型可以應用于實際工程。圖9為A、B兩組4個死亡位置的煙氣毒性評價曲線。由圖9可見，B組中死亡位置的火災煙氣FED 值均超過致死臨界值1.0，其中1號監測點的毒性最強，FED 最高值為6.9，2號監測點毒性最弱，FED 最高值為4.1，且所有的死亡位置均在260～380s之間達到致死臨界值，但值得注意的是，這段時間內4個監測點的溫度均未達到100 ℃；而A 組評價結果表明該火災煙氣毒性始終未達到致死臨界值，1號監測點煙氣的FED 值最高只有0.74。

圖9 A、B兩組4個死記位置煙氣毒性評價曲線Fig.9 Curves of toxic potency measurement at the four dead locations in group A and group B

實際火災調查表明，B 組的評價結果更符合實際。在火災煙氣其他成分接近的情況下，B 組的煙氣毒性預測值超過A 組接近一個數量級，說明含有HCN 的多組分火災煙氣毒性遠高于不含HCN 的煙氣，也就是說，在有大量聚氨酯燃燒的火場環境中，HCN 的存在極大地增加了煙氣的毒性，它對于多組分火災煙氣的耦合毒性具有重要影響。

4 結論

（1）本文在大渦模擬中引入EDC模型，實現了全尺度火災場景中復雜化學反應的計算和毒性產物的捕集，并以某沙發作坊火災為例進行了火災場景數值重構，測量了包括HCN 氣體在內的毒性產物產量，同時將火災熱釋放速率、火場溫度和CO 氣體濃度的模擬結果與未嵌入EDC模型的CFD 軟件計算結果進行了對比，表現出高度的一致性和可行性。新模型的建立實現了利用EDC 模型評估火災煙氣毒性的方法，為火災中HCN 及其他毒性氣體的捕集及毒性分析提供了參考。

（2）利用N-GAS模型來評價某沙發作坊火災煙氣綜合毒性，結果表明：含有HCN 煙氣的毒性評價值超出不含HCN 的煙氣一個數量級，在起火的初始階段就達到了危險臨界值，與實際火災調查結果一致，死亡原因系煙氣中毒而非高溫；HCN 的存在極大地增加了煙氣的毒性，表明其對多組分火災煙氣的耦合毒性起著主導作用。

［1］Lattimer B Y.The Transport of High Concentrations of Carbon Monoxide to Locations Remote from the Burning Compartment［R］.National Institute of Standards and Technology，1996.

［2］Babrauskas V，Gann R G，Levin B C，et al.A methodology for obtaining and using toxic potency data for fire hazard analysis［J］.Fire Safety Journal，1998，31（4）：345-358.

［3］Stec A A，Hull T R，Purser J A，et al.Comparison of toxic product yields from bench-scale to ISO room［J］.Fire Safety Journal，2009，44（1）：62-70.

［4］Zheng X，Wang G，Xu W.Roles of organically-modified montmorillonite and phosphorous flame retardant during the combustion of rigid polyurethane foam［J］.Polymer Degradation and Stability，2014，101：32-39.

［5］Chen X，Huo L，Jiao C，et al.TG-FTIR characterization of volatile compounds from flame retardant polyurethane foams materials［J］.Journal of Analytical and Applied Pyrolysis，2013，100：186-191.

［6］黃帥，陳開巖，湯燕飛，等.單層大空間建筑內防火隔離帶設計與計算［J］.安全與環境工程，2014，21（1）：112-115.

［7］鄭梓德，侯龍飛.自動擋煙垂壁對隧道火災的控制研究［J］.安全與環境工程，2011，18（5）：69-73.

［8］Wesolek D，Kozlowski R.Toxic gaseous products of thermal decomposition and combustion of natural and synthetic fabrics with and without flame retardant［J］.Fire and Materials，2002，26（4／5）：215-224.

［9］Ferrari L A，Arado M G，Giannuzzi L，et al.Hydrogen cyanide and carbon monoxide in blood of convicted dead in a polyurethane combustion：aproposition for the data analysis［J］.Forensic Science International，2001，121（1）：140-143.

［10］Babrauskas V，Levin B C，Gann R G，et al.Toxic potency measurement for fire hazard analysis［J］.Fire Technology，1992，28（2）：163-167.

［11］Bustamante V L，Rogaume T，Guillaume E，et al.Analysis of principal gas products during combustion of polyether polyurethane foam at different irradiance levels［J］.Fire Safety Journal，2009，44（7）：933-940.

［12］Magnussen B F.On the structure of turbulence and a generalized eddy dissipation concept for chemical reaction in turbulent flow［C］／／19thAIAA Meeting.St.Louis，USA，1981.

［13］Ertesvag I S，Magnussen B F.The eddy dissipation turbulence energy cascade model［J］.Combustion Science and Technology，2000，159（1）：213-235.

［14］Magnussen B F.The eddy dissipation concept a bridge between science and technology［C］／／ECCOMAS Thematic Conference on Computational Combustion.Lisbon，Portugal，2005：21-24.

［15］Wang H Y.Numerical and theoretical evaluations of the propagation of smoke and fire in a full-scale tunnel［J］.Fire Safety Journal，2012，49：10-21.

［16］Peters A A F，Weber R，Mathematical modeling of a 2.25MW swirling natural gas flame.Part 1：Eddy break-up concept for turbulent combustion；probability density function approach for nitric oxide formation［J］.Combustion Science and Technology，1995，110（1）：67-101.

［17］Chen Z，Wen J，Xu B，et al.Extension of the eddy dissipation concept and smoke point soot model to the LES frame for fire simulations［J］.Fire Safety Journal，2014，64：12-26.

［18］張兆順，崔桂香，許春曉.湍流大渦數值模擬的理論和應用［M］.北京：清華大學出版社，2005.

［19］周穎.隧道火災煙氣流動的數值模擬研究［J］.安全與環境工程，2014，21（3）：140-143.

［20］霍然，胡源，李元洲.建筑火災安全工程導論［M］.合肥：中國科學技術大學出版社，1999.

［21］Ernst A，Zibrak J D.Carbon monoxide poisoning［J］.New England Journal of Medicine，1998，339（22）：1603-1608.

［22］Gupta R C.Handbook of Toxicology of Chemical Warfare Agents［M］.New York：Academic Press，2009.

［23］黎強，劉清輝，張慧，等.火災煙氣中有毒氣體的體積分數分布與危害［J］.自然災害學報，2003，12（3）：69-74.

［24］Magnusson R，Nyholm S，Stot C.Analysis of hydrogen cyanide in air in a case of attempted cyanide poisoning［J］.Forensic Science International，2012，222（1）：e7-e12.

［25］World Health Organization.Concise international chemical assessment document 61，Hydrogen cyanide and cyanides：human health aspects［J］.Indian Journal of Medical Research，2005，122（2）：180-182.