基于形態(tài)濾波和EMD-AR譜的軸承故障特征提取

劉繼承,聶品磊,佟 宇

（東北石油大學(xué) 電氣信息工程學(xué)院，遼寧 大慶 163318）

基于形態(tài)濾波和EMD-AR譜的軸承故障特征提取

劉繼承,聶品磊,佟 宇

（東北石油大學(xué) 電氣信息工程學(xué)院，遼寧 大慶 163318）

將AR譜估計(jì)與EMD方法結(jié)合，應(yīng)用組合形態(tài)濾波對(duì)故障信號(hào)進(jìn)行降噪預(yù)處理，對(duì)預(yù)處理后的信號(hào)進(jìn)行EMD分解，之后對(duì)各階IMF做AR譜估計(jì)并集總平均，從而提取振動(dòng)信號(hào)的故障特征頻率。文中所述算法能夠避免HHT方法中Hilbert變換所產(chǎn)生的難以解釋的負(fù)頻率，較準(zhǔn)確地提取出滾動(dòng)軸承振動(dòng)信號(hào)的故障特征頻率，從而為滾動(dòng)軸承振動(dòng)信號(hào)的檢測(cè)與故障診斷研究提供參考意見(jiàn)。

振動(dòng)與波；形態(tài)濾波；滾動(dòng)軸承；EMD；IMF；AR譜

旋轉(zhuǎn)機(jī)械是電力、化工、冶金和機(jī)械制造等重要工程領(lǐng)域中的關(guān)鍵設(shè)備，滾動(dòng)軸承是旋轉(zhuǎn)機(jī)械中極為重要的部件，對(duì)其工作時(shí)產(chǎn)生的振動(dòng)信號(hào)進(jìn)行分析并從中發(fā)現(xiàn)潛在的故障能夠有力保障設(shè)備的正常運(yùn)行。目前主要的振動(dòng)信號(hào)故障特征提取方法包括[1]：小波變換（WT）、現(xiàn)代譜分析、主元分析（Principal Component Analysis，PCA）、獨(dú)立分量分析（Independent Component Analysis，ICA）、高階統(tǒng)計(jì)量分析以及被引入旋轉(zhuǎn)機(jī)械故障診斷領(lǐng)域的混沌與分形動(dòng)力系統(tǒng)理論。Huang等人于1998年提出了HHT(Hilbert Huang Transform)方法[2]，該方法先對(duì)信號(hào)進(jìn)行經(jīng)驗(yàn)?zāi)B(tài)分解（Empirical Mode Decomposition，EMD），然后對(duì)內(nèi)模函數(shù)（Intrinsic Mode Function，IMF）做Hilbert變換得到信號(hào)的瞬時(shí)頻率等故障信息。HHT方法雖然適合處理非線性、非平穩(wěn)信號(hào)，但信號(hào)中混有的噪聲，會(huì)使EMD產(chǎn)生模態(tài)裂解現(xiàn)象；此外，Hilbert變換會(huì)產(chǎn)生難以解釋的負(fù)頻率。針對(duì)HHT算法所存在的不足，孟宗等提出用小波改進(jìn)閾值去噪與經(jīng)驗(yàn)?zāi)B(tài)分解結(jié)合的方法來(lái)提取旋轉(zhuǎn)機(jī)械故障特征，以提高故障診斷準(zhǔn)確率[3]；陳長(zhǎng)征等提出將EMD產(chǎn)生的殘差分量與原信號(hào)間的相關(guān)系數(shù)作為閾值，對(duì)IMF進(jìn)行自適應(yīng)篩選，以判別偽IMF[4]；秦娜等提出用EEMD樣本熵構(gòu)成高維特征矢量，提取告訴列車(chē)轉(zhuǎn)向架故障特征[5]；馬銀戌等提出用二次EEMD分解來(lái)減小模態(tài)混疊[6]；夏均忠等提出EMD分形技術(shù)提取變速器軸承故障特征[7]；錢(qián)強(qiáng)等將振動(dòng)監(jiān)測(cè)技術(shù)應(yīng)用到旋轉(zhuǎn)機(jī)械故障診斷中[8]。本文使用形特征態(tài)濾波EMD-AR譜方法對(duì)故障信號(hào)進(jìn)行處理，能夠減小EMD中的模態(tài)裂解現(xiàn)象，同時(shí)避免Hilbert變換產(chǎn)生的無(wú)法解釋的負(fù)頻率，能夠較準(zhǔn)確地提取出信號(hào)中的故障特征頻率。首先闡述了用于信號(hào)預(yù)處理的形態(tài)濾波算法和EMD-AR譜算法的基本原理，之后使用美國(guó)凱斯西儲(chǔ)大學(xué)滾動(dòng)軸承數(shù)據(jù)中心提供的振動(dòng)信號(hào)進(jìn)行實(shí)驗(yàn)。通過(guò)與故障信號(hào)的FFT譜的對(duì)比，可以看出此方法可以較準(zhǔn)確地提取出信號(hào)的故障特征頻率。

1 算法簡(jiǎn)介

振動(dòng)信號(hào)中含有的大量噪聲是導(dǎo)致EMD發(fā)生模態(tài)裂解現(xiàn)象的一個(gè)重要原因，采用合理的降噪方法對(duì)信號(hào)降噪，能夠有效地減小EMD的模態(tài)裂解現(xiàn)象，從而提高故障特征提取精度。數(shù)學(xué)形態(tài)學(xué)具有計(jì)算簡(jiǎn)單、實(shí)用性好、時(shí)延較小等優(yōu)點(diǎn)，其對(duì)信號(hào)的處理完全在時(shí)域中進(jìn)行,是一種高效的振動(dòng)信號(hào)降噪新方法。

分別采用結(jié)構(gòu)元素為三角型的組合形態(tài)濾波器和小波閾值降噪對(duì)故障信號(hào)進(jìn)行降噪處理。通過(guò)實(shí)驗(yàn)可以看出，組合形態(tài)濾波后的故障信號(hào)與原故障信號(hào)的相關(guān)系數(shù)為0.858 3，而小波閾值去噪后的故障信號(hào)與原故障信號(hào)的相關(guān)系數(shù)為0.731 7。可以看出，通過(guò)形態(tài)組合濾波，信號(hào)中的噪聲明顯減少，且去噪效果較好。上述結(jié)果說(shuō)明形態(tài)組合濾波能有效的減小噪聲干擾，通過(guò)形態(tài)組合濾波對(duì)信號(hào)進(jìn)行降噪處理是可行的。

現(xiàn)有如式(1)所示信號(hào)，其中f1=10 Hz,f2=50 Hz。

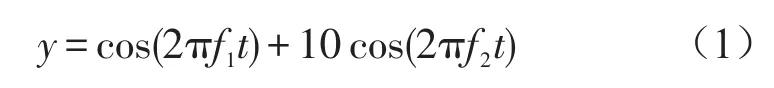
對(duì)式（1）中的模擬信號(hào)加入信噪比為10的高斯噪聲，對(duì)含有噪聲的模擬信號(hào)以及用組合形態(tài)濾波方法去噪后的模擬信號(hào)進(jìn)行EMD分解，其結(jié)果如圖1所示

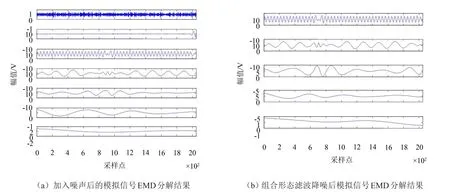
圖1 模擬信號(hào)EMD分解結(jié)果

從圖1（a）中可以發(fā)現(xiàn)，由于噪聲的干擾，造成EMD分解過(guò)程中，分解層數(shù)增多產(chǎn)生了模態(tài)混疊現(xiàn)象；從圖1（b）中不難看出，通過(guò)形態(tài)濾波方法對(duì)信號(hào)進(jìn)行了預(yù)處理，濾除了信號(hào)中的大部分噪聲，排除了噪聲對(duì)EMD的干擾，從而間接地降低了模態(tài)混疊效應(yīng)，可以看出形態(tài)濾波方法具有一定的抑制模態(tài)混疊的作用。

AR譜估計(jì)是一種時(shí)間序列分析法，其對(duì)時(shí)間序列信號(hào)建立AR模型，再用模型系數(shù)計(jì)算信號(hào)的自功率譜[9]。假定u(n)、x(n)是實(shí)平穩(wěn)的隨機(jī)信號(hào)，u(n)為白噪聲信號(hào)，σ2為其方差，則AR模型的Yule-Walker方程為

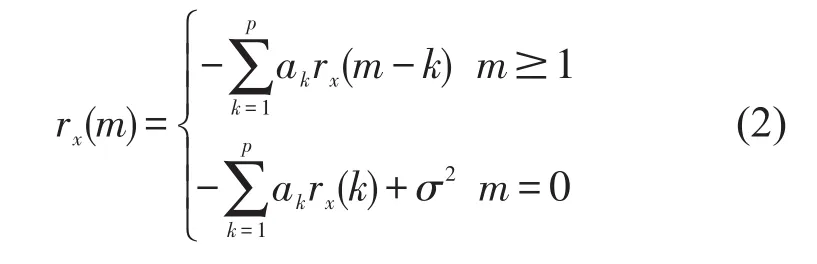
式（2）中p是AR模型的階數(shù)，rx(m)是信號(hào)x(n)的自相關(guān)函數(shù)。從式（2）可以看出一個(gè)p階的AR模型共有p+1個(gè)參數(shù)，即a1,a2,…,ap,σ2，只要知道x(n)的前p+1個(gè)自相關(guān)函數(shù)rx(0)、rx(1)、…、rx(p)，即可由式（2）的線性方程組求出這p+1個(gè)系數(shù)。

將所求得的p+1個(gè)參數(shù)代入下式

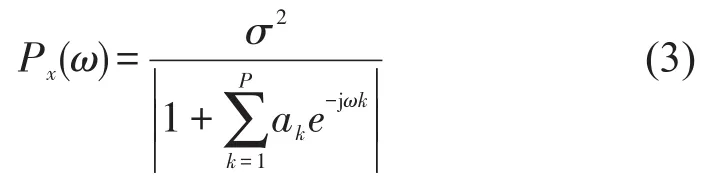
即可求出x(n)的功率譜。

假定信號(hào)x(n)可以被分解為i個(gè)IMF，對(duì)IMF的AR譜集總平均得到信號(hào)的AR譜為

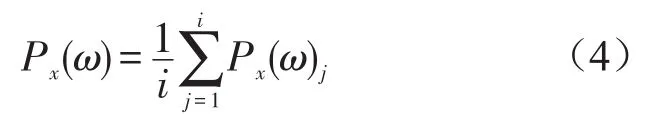
對(duì)式（1）中的模擬信號(hào)相應(yīng)IMF的AR譜集總平均，得到模擬信號(hào)的AR譜如圖2所示，從圖中可以看出本算法能夠準(zhǔn)確提取出模擬信號(hào)中包含的兩個(gè)頻率分量50 Hz、10 Hz。

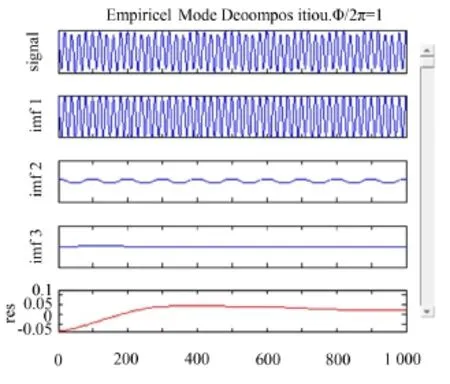
圖2 仿真信號(hào)及各階IMF分量

綜上，形態(tài)濾波EMD-AR法的基本過(guò)程如下：首先用形態(tài)濾波方法對(duì)信號(hào)降噪預(yù)處理，之后對(duì)預(yù)處理后的信號(hào)進(jìn)行EMD分解，最后對(duì)各階IMF函數(shù)做AR譜估計(jì)并集總平均。

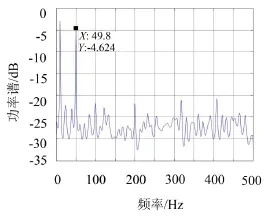
圖3 模擬仿真信號(hào)的AR譜

2 滾動(dòng)軸承振動(dòng)信號(hào)故障特征提取

根據(jù)滾動(dòng)軸承的運(yùn)動(dòng)分析，Balderston于1969年得出滾動(dòng)軸承的故障頻率計(jì)算公式[10]。

式中n為滾動(dòng)體數(shù)目；d為滾動(dòng)體直徑；D為軸承節(jié)徑；θ為接觸角（推力軸承接觸角θ為90°）；f0為轉(zhuǎn)軸旋轉(zhuǎn)頻率。軸承在對(duì)應(yīng)的轉(zhuǎn)速下的故障特征頻率為故障頻率乘以相應(yīng)的轉(zhuǎn)速頻率。

這里所用的實(shí)驗(yàn)數(shù)據(jù)來(lái)源于美國(guó)凱斯西儲(chǔ)大學(xué)（Case Western Reserve University，CWRU）滾動(dòng)軸承數(shù)據(jù)中心。所用數(shù)據(jù)為植入內(nèi)環(huán)故障的滾動(dòng)軸承振動(dòng)加速度信號(hào)，電機(jī)轉(zhuǎn)速為1797轉(zhuǎn)/分，采樣頻率為12 kHz。軸承型號(hào)為6205-2RSJEM SKF型深溝軸承。軸承內(nèi)徑為25 mm；外徑為51 mm；厚度為15 mm；滾動(dòng)體直徑為8 mm；截圓直徑為39 mm。

由式(5)及軸承尺寸數(shù)據(jù)可計(jì)算出實(shí)驗(yàn)中使用的滾動(dòng)軸承內(nèi)圈故障頻率約為162 Hz。實(shí)驗(yàn)中使用的故障信號(hào)如圖4所示，其EMD分解結(jié)果如圖5所示。計(jì)算得到的故障信號(hào)AR譜如圖6所示，其中164 Hz為振動(dòng)信號(hào)的故障特征頻率，與信號(hào)的故障特征頻率理論值非常接近；同時(shí)AR譜中還存在滾動(dòng)軸承故障特征頻率的二次諧波，以及軸承轉(zhuǎn)動(dòng)頻率的高次諧波。通過(guò)與圖7中FFT譜相對(duì)比可以明顯看出本文所采用的方法得到的故障頻率準(zhǔn)確率較高。

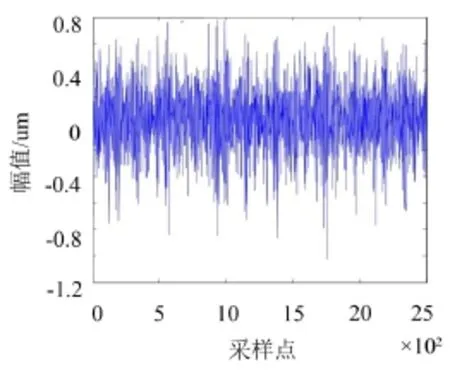
圖4 截取2 500個(gè)采樣點(diǎn)的故障信號(hào)

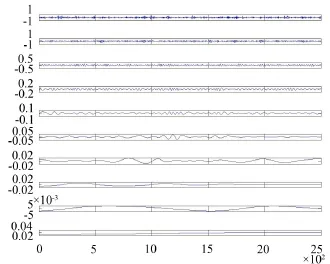
圖5 故障信號(hào)EMD分解結(jié)果

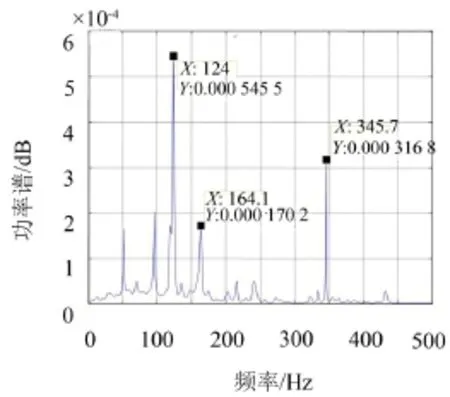
圖6 故障信號(hào)AR譜

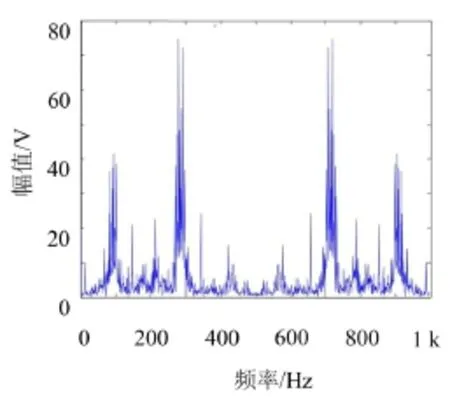
圖7 故障信號(hào)的FFT譜

4 結(jié)語(yǔ)

將形態(tài)濾波與EMD-AR譜方法相結(jié)合提取滾動(dòng)軸承的故障頻率，實(shí)驗(yàn)結(jié)果說(shuō)明該方法能夠較準(zhǔn)確地提取出信號(hào)的故障特征頻率。采用形態(tài)濾波方法對(duì)信號(hào)去噪能減小EMD分解時(shí)的模態(tài)裂解現(xiàn)象，提高故障特征提取的精度；EMD與AR譜的結(jié)合避免了Hilbert變換中無(wú)法解釋的負(fù)頻率。采用有效的方法對(duì)數(shù)據(jù)進(jìn)行延拓改進(jìn)EMD方法，進(jìn)一步提高故障頻率提取精度是后續(xù)的研究方向。

[1]張韌.旋轉(zhuǎn)機(jī)械故障特征提取技術(shù)及其系統(tǒng)研究[D].杭州：浙江大學(xué)，2004.

[2]Huang.The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis[C].Proc.R.Soc.A,1998,454(6):903-995.

[3]孟宗，李?yuàn)檴?小波改進(jìn)閾值去噪和經(jīng)驗(yàn)?zāi)B(tài)分解相結(jié)合的旋轉(zhuǎn)機(jī)械故障特征提取[J].機(jī)械強(qiáng)度，2014，36（1）：024-029.

[4]陳長(zhǎng)征，孫鮮明，周 勃，等.HHT改進(jìn)及其在風(fēng)力發(fā)電機(jī)故障診斷中的應(yīng)用[J].華東電力，2014，42（6）：1123-1128.

[5]秦娜，金煒東，黃進(jìn)，等.基于EEMD樣本熵的高速列車(chē)轉(zhuǎn)向架故障特征提取[J].西南交通大學(xué)學(xué)報(bào)，2014，49（1）:27-32.

[6]馬銀戌.基于二次EEMD的轉(zhuǎn)子故障信號(hào)時(shí)頻分析方法研究[J].科學(xué)技術(shù)與工程，2014，14（21）：113-117.

[7]夏均忠，劉遠(yuǎn)宏.基于EMD分形技術(shù)提取變速器軸承故障特征[J].噪聲與振動(dòng)控制，2012，32（2）：119-122.

[8]錢(qián)強(qiáng).振動(dòng)監(jiān)測(cè)技術(shù)在旋轉(zhuǎn)機(jī)械故障診斷中的應(yīng)用[J].噪聲與振動(dòng)控制，2014，34（2）：164-168.

[9]王志剛，李友榮.小波分析-AR譜及其工程應(yīng)用[J].振動(dòng)與沖擊，2001，20（1）：85-87.

[10]賈艷秋，張兵，陳雪梅.滾動(dòng)軸承的故障機(jī)理及診斷[J].化工裝備技術(shù)，2011，32（4）：55-57.

Extraction of Fault Features for Bearings Based on Morphological Filtering and EMD-AR Spectrum

LIU Ji-cheng,NIE Pin-lei,TONG Yu
(School of Electrical and Information Engineering,Northeast Petroleum University, Daqing 163318,Liaoning China)

Combining the AR spectrum estimation method with EMD,the morphological filtering was applied to denoising pre-process of the fault signal.Then,the signal was decomposed by using EMD.The AR spectrum of each order IMF was estimated.The average value of the AR spectrums was calculated.Finally,the fault characteristic frequency of the vibration signal was extracted.In this method,the negative frequency generated by Hilbert transform in HHT can be avoided,and the fault characteristic frequency of rolling bearings can be extracted.This work may provide a reference for vibration detection and fault diagnosis of rolling bearings.

vibration and wave;morphological filtering;rolling bearing;EMD;IMF;AR spectrum

TH165+.3

A

10.3969/j.issn.1006-1335.2015.03.034

1006-1355(2015)03-0159-04

2014－12－31

黑龍江省長(zhǎng)江學(xué)者后備支持計(jì)劃（2012CJHB005）

劉繼承（1970－），男，博士生導(dǎo)師；主要研究方向：非平穩(wěn)信號(hào)分析、地震信號(hào)處理。

聶品磊，男，碩士生。E-mail:niepinlei@126.com