車輛懸掛功率反饋主動控制算法

張 磊，張進秋，畢占東，何 旭，王興野

（裝甲兵工程學院 裝備試用與培訓大隊，北京 100072）

車輛懸掛功率反饋主動控制算法

張 磊，張進秋，畢占東，何 旭，王興野

（裝甲兵工程學院 裝備試用與培訓大隊，北京 100072）

以提高車輛減振性能為目的，提出一種基于降低懸掛系統傳遞至車體平均功率的功率反饋主動控制算法。以某輪式車輛四分之一車輛二自由度懸掛系統模型為研究對象，基于時域和頻域相結合的方法對算法性能進行分析和評價，并分析權重系數取值對算法性能的影響。結果表明：功率反饋控制算法能夠顯著改善車輛的乘坐舒適性和操縱穩定性，提高車輛減振性能。

振動與波；懸掛系統；主動控制算法；功率反饋

懸掛是車輛的重要組成部分，彈性連接車體和車輪，衰減車輛運行過程中由于不平路面激勵傳遞至車體的振動。研究表明，懸掛性能對車輛的乘坐舒適性、操縱穩定性等行駛相關的重要特性有直接影響[1,2]。目前，絕大部分車輛仍采用被動懸掛，其懸掛參數不可調，難以適應復雜行駛路面環境的需求。基于主動、半主動控制的可控懸掛是提高懸掛性能的公認有效途徑。其中，主動懸掛性能最優，是車輛可控懸掛技術的發展方向，而行之有效的控制算法一直是主動懸掛設計和開發的關鍵問題。

關于可控懸掛控制算法的研究幾乎涵蓋了所有先進的控制理論和控制方法，一些成熟的算法，如天棚控制[3]、最優控制[4]、魯棒控制[5]、模糊控制[6]以及神經網絡控制[7]的性能都已得到分析和驗證。近年來，一些學者基于能量流分析的方法探索懸掛系統輸入到車體的平均功率對車輛減振性能的影響，得到的結論是通過降低輸入到車體的平均功率有助于提高車輛的減振性能[8,9]，但設計的算法是一種頻域最優控制模型，需要實時獲取路面的輸入頻率，無法工程實現。

本文以提高車輛的減振性能為目標，基于降低懸掛系統輸入到車體的平均功率的考慮，提出適用于車輛懸掛的功率反饋主動控制算法，并以被動懸掛和天棚主動懸掛為參照，對該算法性能進行分析和評價。

1 懸掛系統動力學模型及分析

四分之一車二自由度懸掛系統模型相對簡單，且能夠較為真實地反映車輛垂直方向的基本振動特性，常用作懸掛系統概念設計、控制算法驗證的基礎[1]，故本文基于該模型進行主動控制算法設計和性能分析。

對于采用獨立懸掛的車輛，假設其質量分配系數為1，且僅考慮垂直運動方向的振動，可建立如圖1所示的1/4車二自由度主動懸掛系統動力學模型。假設坐標原點選在各自平衡位置，則主動懸掛系統的力學方程為

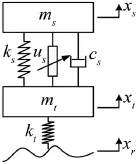
圖1 主動懸掛系統動力學模型

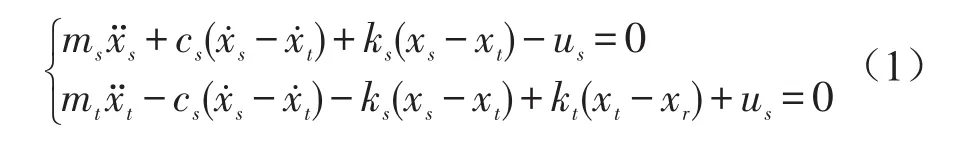
式中ms和mt分別為車體和車輪的質量；ks和kt分別為懸掛彈簧和車輪的剛度；cs為懸掛系統阻尼系數；xs、xt和xr分別為車體、車輪的垂直位移和路面不平度激勵；us為主動控制力。

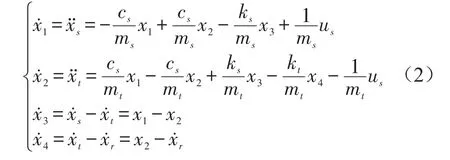
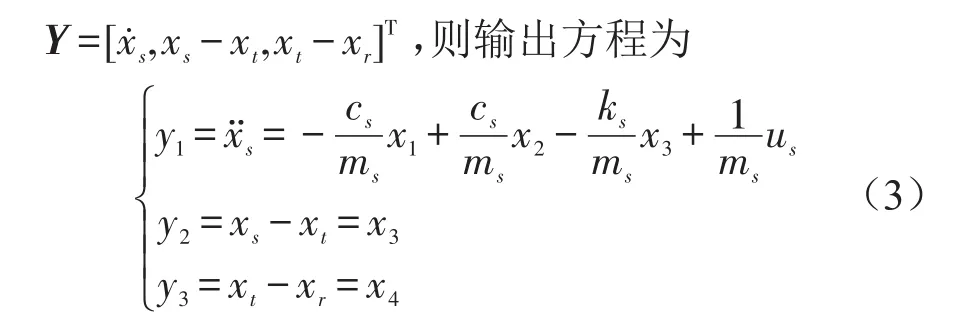
取U=us為控制變量、干擾，則懸掛主動控制系統狀態方程式可表示為

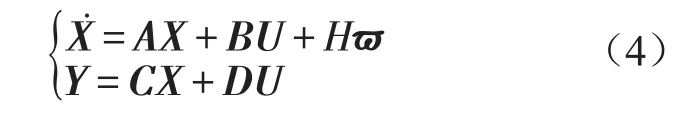
式中

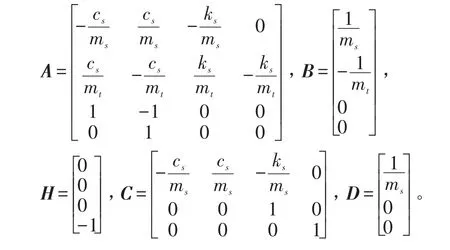
2 控制算法設計

功率是作用于系統某一點的力與速度的乘積。對于振動控制系統，它綜合考慮了力和速度對系統的影響。振動控制領域的功率流理論常用平均功率反映系統輸入功率的大小，即

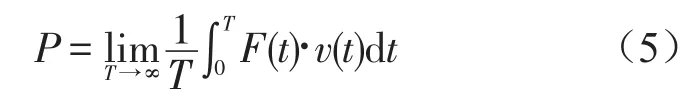
式中F(t)作用于系統的外力，v(t)為系統產生的速度響應。

對于懸掛系統振動模型，以車體為研究對象，它受到的合外力為懸掛彈簧、阻尼器及作動器對車體作用力的合力，由式（1）得

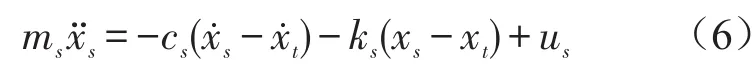
則懸掛系統輸入到車體的功率為

本文算法設計以傳遞至車身的功率最小為控制目標，提出車輛懸掛功率反饋（Power Feedback，簡稱PF）控制算法，并基于最優控制理論實現并分析該算法。

以減小懸掛輸入到車體的功率為控制目標，以作動器出力為約束條件，建立性能泛函

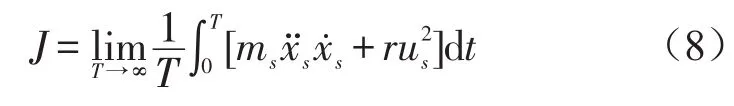
式中控制目標的權重系數取1，r為約束條件的權重系數。由于算法中控制目標和約束條件各只有一個，避免了復雜的權重系數取值多目標優化問題。

將式（8）中的狀態變量和控制變量通過狀態方程的形式表示出來，即

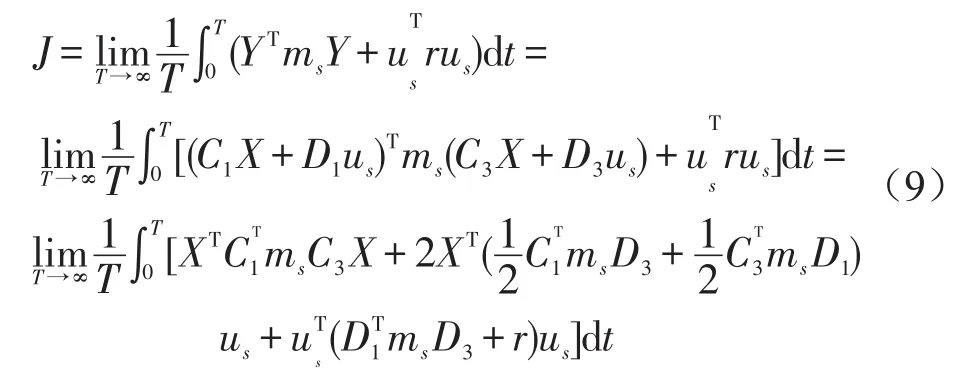
式中Ci、Di分別為狀態矩陣C、D的第i行。

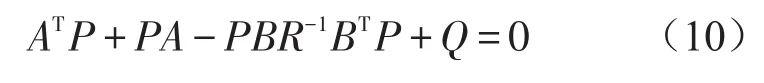
因而根據任意時刻t的狀態反饋變量X，就可以求出該時刻作動器的最優控制力

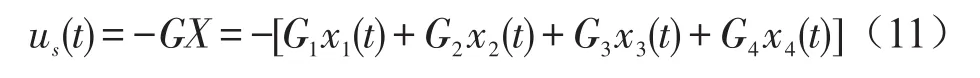
顯然，PF主動控制算法是一種以限制車體輸入功率為目標的全狀態反饋控制，其中車輪動變形的狀態一般難以直接測量，工程中可以采用狀態預估的方式獲取，最常用的方法是基于Kalman濾波器進行預估，具體方式此處不再贅述。

3 性能分析與評價

為分析功率PF控制算法的有效性，采用車輛懸掛振動控制領域常用的天棚主動控制算法為對比，基于Matlab/Simulink分別建立被動懸掛、天棚（Skyhook，簡稱SH）主動懸掛和PF主動懸掛系統動力學模型，從時域和頻域的角度對算法性能進行分析評價。其中，對應式（1）所示動力學模型的SH主動控制算法，其控制力為

式中csky為天棚阻尼系數。

以某型輪式車輛為研究對象，被動懸掛系統參數如表1所示。其中，被動懸掛的車輪靜變形為0.019 m，假設懸掛許用動行程為±0.1 m。

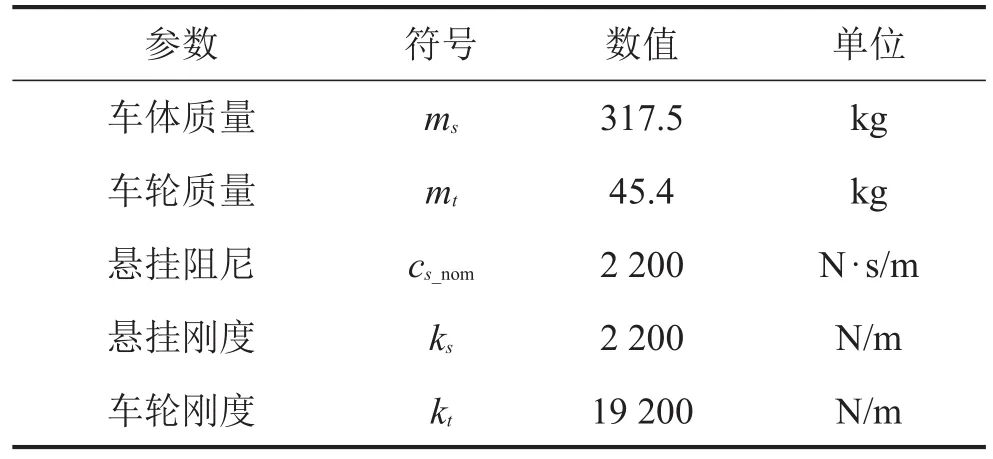
表1 被動懸掛系統懸掛參數

SH主動控制算法中，通常情況下csky取值越大，車輛的乘坐舒適性和操縱穩定性越好，故本文取較大的天棚阻尼系數csky=2 cs_nom=3 000 N·s/m，記作SH主動懸掛；對于PF主動控制算法，為分析權重系數取值對懸掛減振性能的影響，分別取兩組不同權重系數r1=3×10-14，r2=1×10-14，記作PF1和PF2懸掛。

3.1 時域分析

時域分析對確定激勵和隨機激勵兩方面進行響應分析。其中，確定激勵通過三角沖擊來考察懸掛的高頻振動行為，主要考察指標為車體加速度；隨機激勵用于對懸掛性能進行綜合分析。

（1）三角沖擊

假設車輛以2 m/s的速度進行直線行駛，在t=0.5 s時通過高度為5 cm、寬度為20 cm的三角形減速帶，4種懸掛的車體加速度時域曲線如圖2所示。

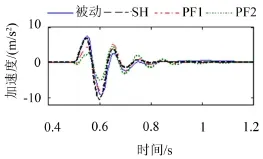
圖2 三角波沖擊響應

由圖2可知，與被動懸掛相比，SH主動控制對車體加速度降低效果十分有限，而PF1控制和PF2控制卻能有效抑制加速度峰值，且PF2控制作用最佳，但一定程度導致了越過障礙后的加速度小幅波動時間變長。在0.4 s～1.2 s范圍內，不同懸掛的車體加速度峰值、均方根值如2表所示。

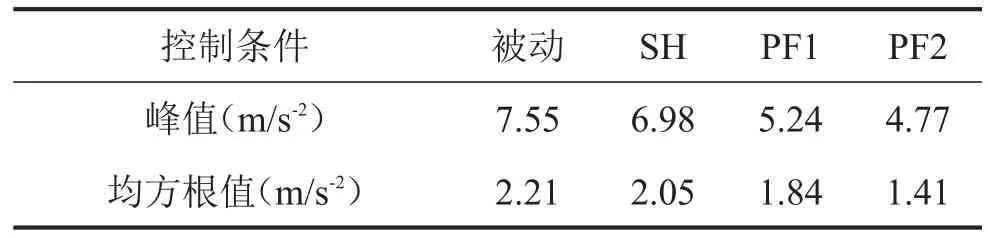
表2 三角波沖擊車體加速度響應

（2）隨機激勵

基于諧波疊加法[10]分別生成車速為20 m/s時C級路面激勵和車速為10 m/s時的D級路面激勵，分析不同懸掛在隨機激勵下各指標的響應。

由于篇幅限制，只給出C級路面下車體加速度、懸掛動行程和車輪動變形的時域曲線，如圖3所示。為直觀起見，本文僅給出了仿真10 s～12 s時長的懸掛各指標時域曲線，整個仿真時段的控制效果對比將通過數據統計的方式進行分析。

計算可得不同行駛工況下三個指標的均方根值和峰值如表3所示。其中，PF1和PF2控制相比于被動懸掛和SH主動懸掛均可大幅降低車體加速度均方根值和峰值，但導致懸掛動行程和車輪動變形峰值和均方根值一定程度增大；PF2對加速度的控制效果優于PF1，但PF2控制下懸掛動行程和車輪動變形增大程度也大于PF1，說明減小權重系數r的取值有助于提高乘坐舒適性，卻一定程度增大了懸掛動行程和車輪動變形，但兩種行駛工況下PF1和PF2控制的懸掛動行程均在許用范圍，并未導致“懸掛擊穿”，D級路面條件下PF2的車輪動變形的峰值明顯大于靜變形，說明該工況下偶爾會出現車輪離地現象。受懸掛固有特性的限制，懸掛各指標之間存在一定約束關系，理論上難以通過控制使懸掛動行程和車輪動變形同時減小。

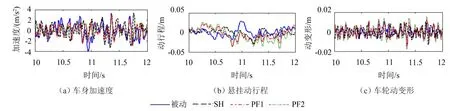
圖3 懸掛各指標時域曲線

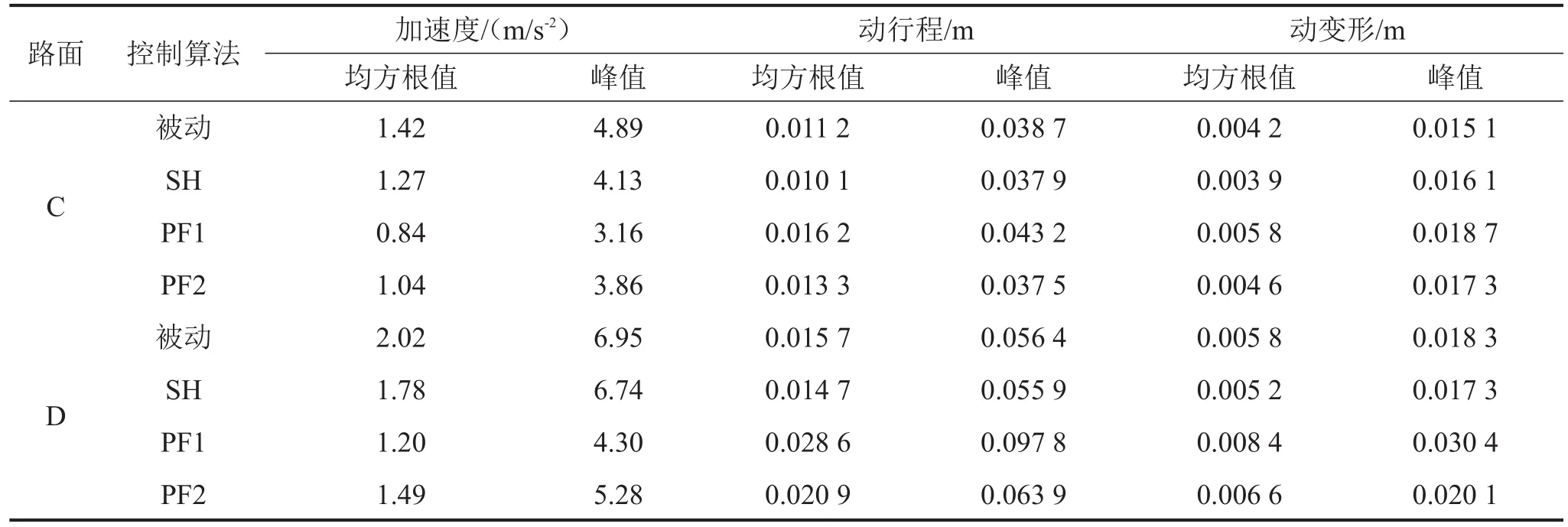
表3 懸掛各指標均方根值和峰值計算結果

3.2 頻域分析

懸掛系統各指標時域統計結果帶有一定隨機性，要全面分析控制算法性能，還需進一步通過頻域分析。不同控制條件懸掛系統各指標傳遞率如圖4所示。由圖4（a）可知，在路面激勵頻率低于車輪共振頻率時，PF控制可以大幅降低車體加速度，且權重系數r取值越小，車體加速度降低程度越大；在路面激勵頻率大于車輪共振頻率時，PF控制對加速度的抑制作用有限，且隨r取值的減小，在高頻區有小幅的控制惡化趨勢，但不明顯；相比之下，SH主動懸掛只能在車體共振區對車體加速度實現有效抑制，其控制效果和有效頻域范圍明顯不及PF控制。由此印證了PF主動控制對車體加速度的抑制效果。

從車輛隔振的角度，懸掛動行程并非越小越好，只需將其限制在設計范圍內，降低發生“懸掛擊穿”的概率即可[11]。“懸掛擊穿”主要發生在振幅較大的低頻區，特別車體共振區。由圖4（b），PF控制和SH控制均能夠明顯降低車輪共振區懸掛動行程的傳遞率，一定程度降低了發生懸掛擊穿的概率，但PF控制導致車輪共振區懸掛動行程有一定程度增大。

由圖4（c），在車輪共振區之前的頻段，PF控制較被動懸掛可有效降低車輪動變形傳遞率，其效果優于SH主動控制；PF控制對車輪動變形的降低幅度隨權重系數r的減小而增大；在車輪共振區，PF控制導致車輪動變形傳遞率有所增大，且隨r的減小動變形傳遞率的增大幅度趨于明顯。

3.3 性能評價

控制算法性能評價主要考慮算法性能對車輛乘坐舒適性和操縱穩定性的影響。目前，車輛乘坐舒適性評價廣泛采用ISO法，該方法以車體加權加速度均方根值為指標；操縱穩定性評價指標通常采用車輪動變形均方根值。上述評價方法存在的不足表現在評價結果受路面狀況和車速等車輛運行工況影響顯著；此外，通過計算動變形均方根值的方法評價操縱穩定性，沒有考慮路面激勵的頻域差別。

針對上述不足，文獻[12]中分別定義了車輛乘坐舒適性和操縱穩定性評價函數，該函數以無控制時的標準被動懸掛為對比，通過傳遞函數頻域加權積分的方法對受算法影響的懸掛性能進行評價，提高了懸掛性能評價的有效性。

乘坐舒適性評價函數定義為

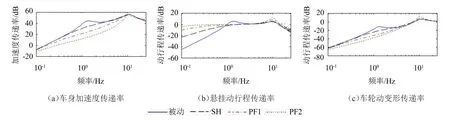
圖4 懸掛傳遞率分析

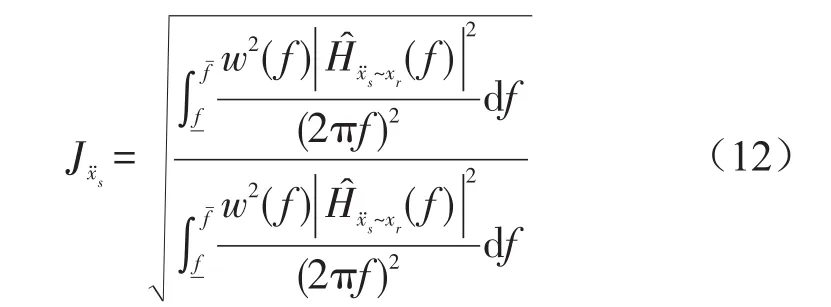
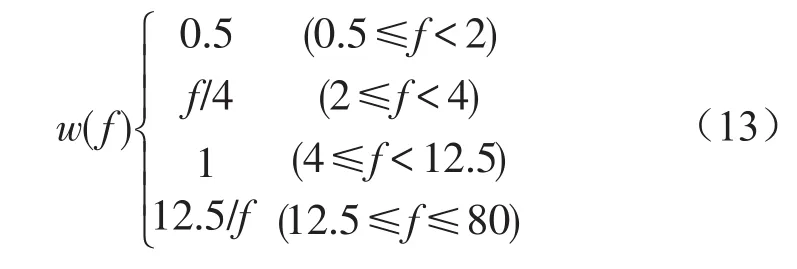
文獻[12]認為，車輪動變形對操縱穩定性的影響具有頻率差別：當路面激勵頻率較低時，動變形處于低谷持續時間較長，對操縱穩定性影響較大；隨著路面激勵頻率的升高，動變形低谷持續時間逐漸變短，對操縱穩定性的影響也越來越小。所以操縱穩定性評價函數定義為

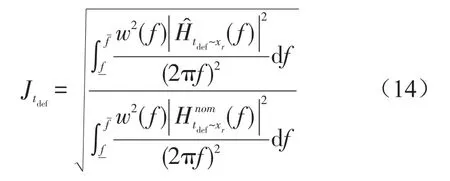
基于上述方法對被動懸掛以及SH、PF1、PF2控制下的主動懸掛性能進行評價和對比，所取頻率范圍為0.5 Hz～25 Hz，該頻率范圍可反映出車體、車輪受懸掛性能影響產生振動的主要動力學特征，其結果如圖6所示。可見，與被動懸掛相比，SH主動控制可使車輛乘坐舒適性提高8.11%，操縱穩定性提高33.32%；PF1控制可使車輛乘坐舒適性提高16.81%，操縱穩定性提高50.49%；在PF2控制下，車輛乘坐舒適性和操縱穩定性分別提高了33.96%和48.86%。評價結果表明，PF控制下懸掛系統的減振性能總體優于SH主動懸掛；PF主動控制算法中，較小的權重系數取值有助于顯著改善車輛乘坐舒適性，而對操縱穩定性的改善程度與權重系數取值較大時相差不多。

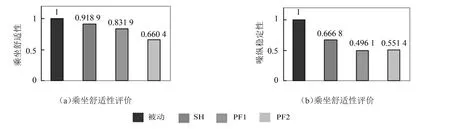
圖6 懸掛性能評價結果

4 結語

為改善車輛的減振性能，提出一種基于降低懸掛系統輸入至車體平均功率的功率反饋主動控制算法。以被動懸掛和天棚主動懸掛為對比對算法性能進行了分析和評價，得到如下結論：

（1）功率反饋主動控制算法能夠在車輪共振區以下的頻段有效降低車體加速度和車輪動變形，顯著改善車輛的乘坐舒適性和操縱穩定性；并較好地抑制了車身共振區的懸掛動行程，一定程度降低了發生“懸掛擊穿”的概率，其總體減振效果明顯優于天棚主動懸掛。

（2）功率反饋主動控制算法的權重系數取值對算法性能有較大影響。較小的權重系數有助于提高車輛乘坐舒適性，而對操縱穩定性影響不大。實際應用中，應根據控制目標合理選擇權重系數。

筆者認為，基于功率分析進行懸掛系統控制算法設計是一種有效的思路和方法，該方法控制目標明確，物理意義清晰，有較大的研究空間。

[1]俞凡，于秀敏.汽車系統動力學[M].北京：機械工業出版社，2008．

[2]董小閔，余淼，廖昌榮，等.汽車磁流變半主動懸架頻域加權次優控制研究[J].系統仿真學報，2006，18（11）：3183-3186．

[3]Karnopp D,Crosby M J,Harwood R A.Vibration control using semi-active force generators[J].ASME Journal of Engineering for Industry,1974,5(2):619-629.

[4]Ercan Y.Optimal control of half-car vehicle model with a variable damping semi-active suspension[C].Proceedings 10 th Int.Conf.on ER&MR,2006:431-437.

[5]Chen H,Liu Z-y,Sun P-y.Application of constrained h∞control to active suspension systems on half-car models [J].Journal of Dynamic Systems,2005,127(3):245-254.

[6]顏文俊，董丹，王維銳，等.非線性半主動懸架系統模糊控制策略[J].控制工程，2011，18（6）：941-946.

[7]王春華，唐焱.車輛主動懸架的BP神經網絡自適應PID控制[J].計算機仿真，2009，26(5)：274-277.

[8]陳昆山，戴建軍，胡思明.基于功率流方法電磁反力混合型主動懸架研究[J].噪聲與振動控制，2008，28(5)：21-24.

[9]劉麗麗.車輛主動懸架系統的功率流傳遞特性及最優控制策略[D].青島：山東科技大學，2004.

[10]段虎明，石峰，謝飛，等.路面不平度研究綜述［J］.振動與沖擊，2009，28(9)：95-101.

[11]Gang Wang.Constant Force Control Methodology for Shock Absorption.US Patent Application［J］.US 2010/ 0332079A1,2010.

[12]彭志召，張進秋，張雨，等.車輛半主動懸掛的頻域控制算法[J].裝甲兵工程學院學報，2013，27(4)：36-42.

Power FeedbackActive ControlAlgorithm for Vehicle’s Suspensions

ZHANG Lei,ZHANG Jin-qiu,BI Zhan-dong,HE Xu,Wang Xing-ye
(Brigade of Equipment Trial and Training,Academy ofArmored Forces Engineering, Beijing 100072,China)

In order to improve vehicle’s shock absorbing property,a power feedback active control algorithm based on the reduction of the average power transferring from suspension systems to vehicle’s body was put forward.The dynamic model of a quarter of the vehicle with a two-DOF suspension was chosen as a research object,and the performance of the control algorithm was analyzed and evaluated in time-domain and frequency-domain.The results show that the power feedback active control can obviously improve riding comfort,handling stability and shock absorbing property of the vehicles.

vibration and wave;suspensions system;active control algorithm;power feedback

U436.33

A

10.3969/j.issn.1006-1335.2015.03.028

1006-1355(2015)03-0130-05+148

2014－12－01

張進秋（1963－），男，博士，教授，博士生導師，主要從事車輛工程、智能材料研制與應用等方面研究工作。E-mail:zhangjq63@163.com