基于Matlab的動力總成懸置系統解耦優化

薛 華，劉志強，劉 巖,蘇 迎

(1.遼寧工程技術大學 機械工程學院，遼寧 阜新 123000；2.華晨汽車工程研究院，沈陽 110000)

基于Matlab的動力總成懸置系統解耦優化

薛 華1，劉志強1，劉 巖2,蘇 迎2

(1.遼寧工程技術大學 機械工程學院，遼寧 阜新 123000；2.華晨汽車工程研究院，沈陽 110000)

以某車型怠速運轉時方向盤劇烈抖動為背景，測量動力總成和懸置參數，建立了動力總成懸置系統的6自由度數學模型，通過解耦計算，發現各個方向耦合比較嚴重，需要進行系統優化設計；應用撞擊中心理論，對前后懸置位置進行調整，然后以懸置系統的剛度、懸置傾斜角度為約束變量，使用Matlab的多目標優化函數fgoalattain，以6個方向的耦合最小為目標函數進行優化設計，結果表明此方法能夠在一定的約束范圍內較好的實現各個方向的解耦，具有較高的實用價值。

振動與波；動力總成；懸置系統；怠速振動；多目標優化；能量解耦

1 懸置

1.1 懸置作用

懸置具有兩方面的要求，一是隔離動力總成的振動向車身的傳遞；二是隔離路面的振動給發動機造成的影響。從舒適性的角度往往希望懸置越軟越好，使振動傳遞率最小，從整車緊湊型來說，由于受發動機艙空間的現在，往往需要較大的剛度，減小振動的位移，這就涉及懸置的三個作用：

支撐作用：將動力總成支撐在車身或者車架上；

限位作用：避免動力總成和其他裝置產生干涉；

隔振作用：隔離發動機振動向車身的傳遞，減小路面激勵向發動機的傳遞。

在發動機橫置、前置前驅的動力總成布置形式中，一般采用三點或者四點支撐，左懸置通常與變速箱連接，在隔離激振的同時起到動力總成限位的作用。右懸置與發動機相連，隔離發動機燃燒激勵、慣性力激勵。前、后懸置通常與變速箱連接布置，承受扭矩，重點起到動力總成的縱向限位。

1.2 設計要求

經客戶反映，某車型在怠速運轉情況下方向盤抖動強烈，初步分析是由于產生共振引起。

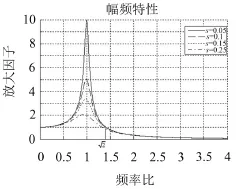
圖1 單自由度振動曲線

由隔振理論可知，理想的懸置設計應該是，在低頻區，高剛度、大阻尼，在高頻區，低剛度、小阻尼[3]。

發動機慣性激振頻率計算公式：f=Q·n/60 Q-比例系數，Q=2

此發動機怠速運轉轉速800 r/min，帶入公式得f=26.7 Hz

路面激勵為2.5 Hz以內，為了避免路面激勵與其他系統產生共振，應使頻率至少大于2 Hz[4]，取最小頻率為5 Hz[5]。

2 數學模型的建立及參數獲取

2.1 建立數學模型

圖2中o-xyz為動力總成坐標系，o為動力總成質心位置，x由質心位置指向發動機前段，z垂直指向氣缸蓋，y由右手定則確定，動力總成具有6個自由度，分別為三個方向的移動和繞三個方向的轉動自由度。懸置簡化為互相垂直的線性彈簧粘性阻尼元件，為分別與(x,y,z)軸平行的坐標系，動力總成采用橫置前置前驅的布置方式[6]。

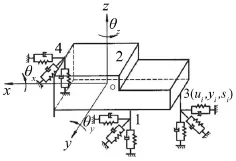
圖2 動力總成懸置系統模型

2.2 初始參數獲取

通過稱得動力總成質量（kg）和用三線擺測得慣性參數（kg·m2）值，如表1。

表1 動力總成的質量和慣性參數

測得動力總成的質心位置相對測量坐標系的位置為（-16.34，49.97，50.42），各個懸置相對質心位置參數，如表2。

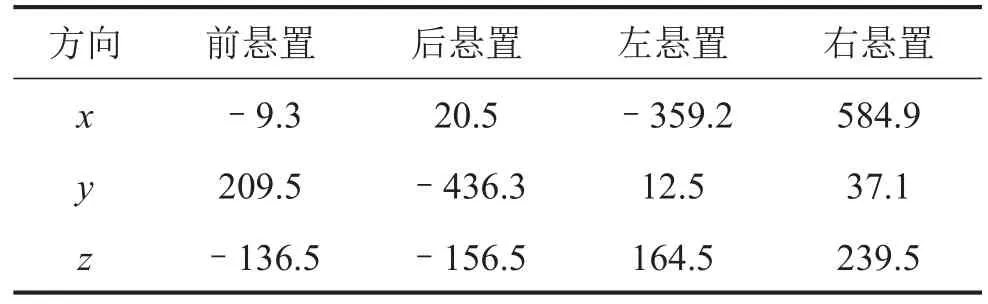
表2 懸置初始位置/mm

通過體積壓縮試驗測得橡膠參數，如表3。

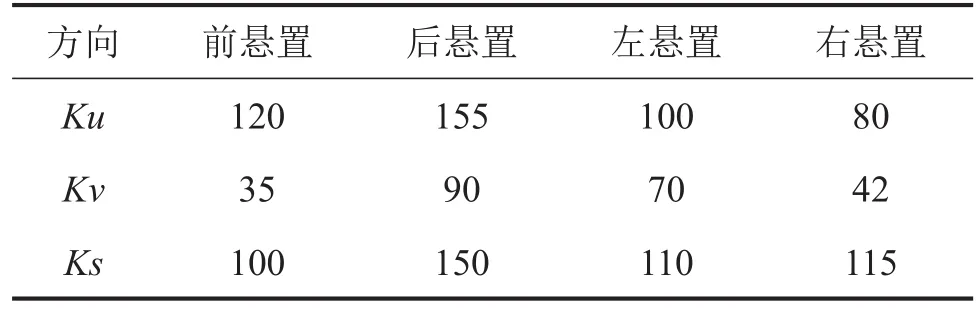
表3 初始剛度值/(N/mm)

測得懸置安裝的初始角度值，如表4。

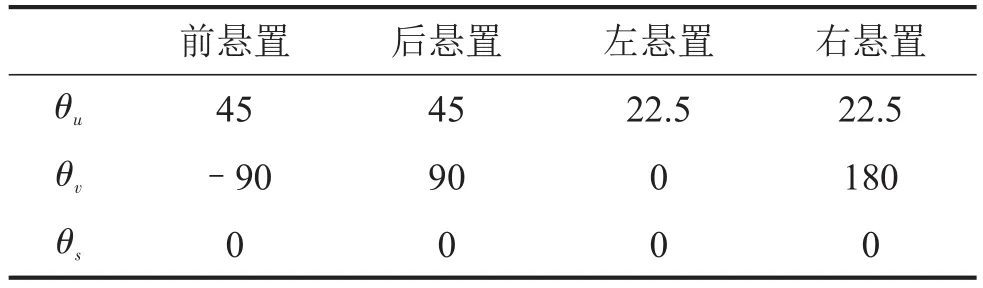
表4 初始角度值/(°)

3 解耦計算

經過在動力總成坐標系下的解耦計算得各個方向的頻率和解耦率，如表5所示。

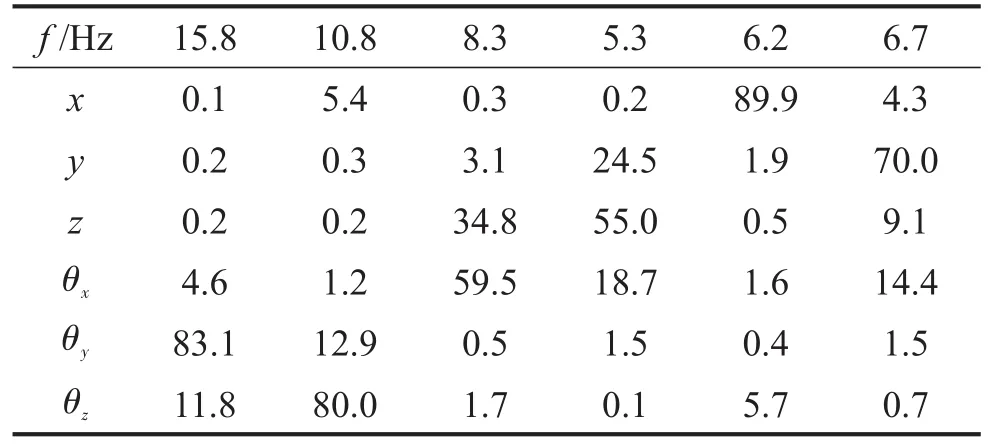
表5 初始頻率和解耦率/(%)

從表5中看出動力總成在z、θx、θy方向的耦合比較嚴重，而且頻率之間間隔較小，容易產生運動耦合，容易與其他部件之間產生振動耦合，引起整車的振動和噪聲，因此需要進行優化設計。

4 優化設計

4.1 能量解耦法

為了避免與其他附屬設備產生共振，同時降低動力總成的振動向車身的傳遞，也就是振動的傳遞率，需進行優化設計。傳遞率與質量、剛度和阻尼有關，由于對于一個現成的動力總成來說，質量是確定性因素，因此需要從剛度和阻尼開展分析，由于阻尼只影響位移，對振動的傳遞率和頻率沒有影響，暫不考慮[7]。

對于發動機橫置前置前驅的動力總成系統，普遍采用能量解耦法進行解耦和優化，通過對懸置剛度、位置和傾斜角度為變量進行優化，得到在怠速工況下，動力總成的頻率合理分布和的解耦率。根據振動理論，動力總成質心運動的數學表達式為

推導得到

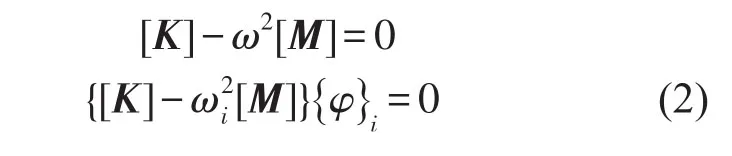
[M]，[K]分別是質量矩陣和剛度矩陣，{φ}為模態矩陣，根據質量矩陣和剛度矩陣可求得固有頻率和振型。當動力總成以第i階固有頻率和振型振動時，第i個坐標上的能量解耦率[7，11]為

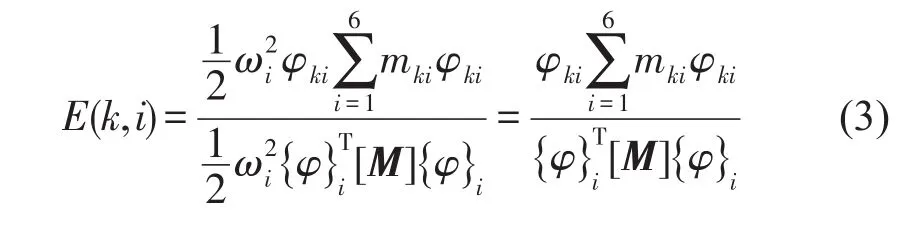
4.2 Matlab多目標優化函數

使用Matlab的多目標優化函數，對各個自由度進行解耦優化，歸結為求的最小值，使得

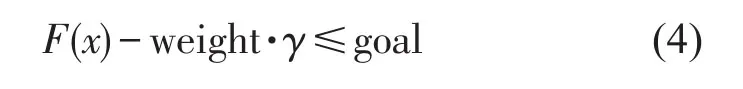
滿足約束條件

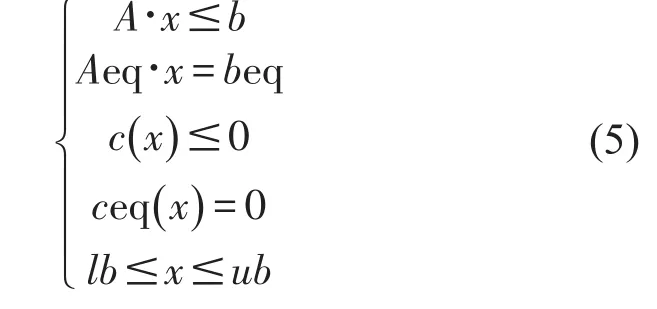
其中x，weight，goal，b，beq，lb和ub是向量，A和Aeq是矩陣；c(x)，ceq(x)和F(x)是向量函數，他們可以使非線性函數。F(x)是所考慮的目標函數，goal是欲達到的目標值，多目標規劃的Matlab函數fgoalattain的用法為

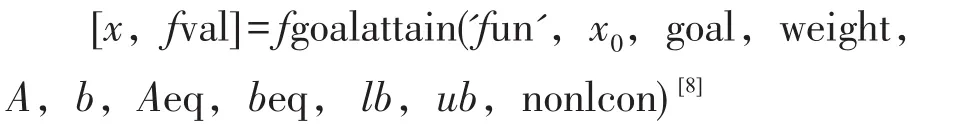
其中 fun是用M文件定義的目標向量函數，x0是初值，weight是權重。A，b定義不等式約束A·x≤0，Aeq，beq定義等式約束Aeq·x=beq，nonlcon是用M文件定義的非線性約束c(x)≤0，ceq(x)=0。返回值 fval是目標向量函數的值。

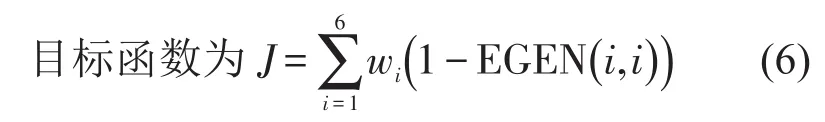
wi為第i階固有頻率的加權因子。懸置上下限約束條件

非線性約束條件

4.3 優化計算

由撞擊中心理論可知，當其中一個位置懸置受到激勵時，另一個懸置不產生運動，可以減少振動向車身的傳遞

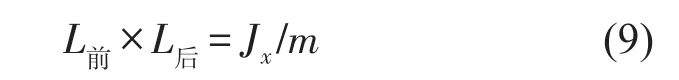
Jx—動力總成繞x軸的轉動慣量

m—動力總成的質量

L前—前懸置到動力總成質心的距離

L后—后懸置到動力總成質心的距離

根據撞擊中心理論,原前后懸置不符合要求，保持后懸置位置不變，調整前懸置的y向的水平距離為170.072，再以懸置剛度（表6）和傾角（表7）為約束條件，設置目標值和各個方向的權重系數為goal=[0.01,0.01,0.01,0.01,0.01,0.01]、weight=[0.01,0.01,0.01，0.01，0.01，0.01]進行優化。得到動力總成在各個方向的剛度，傾斜角度和解耦率[7]。

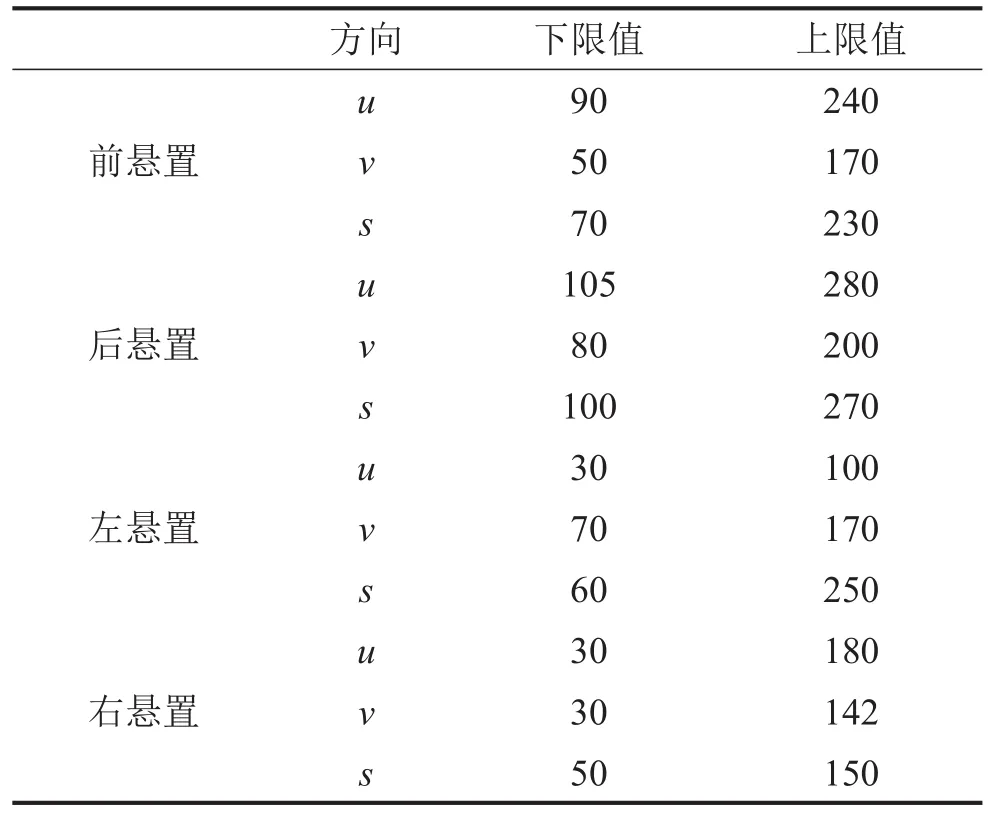
表6 懸置剛度約束范圍/(N/mm)

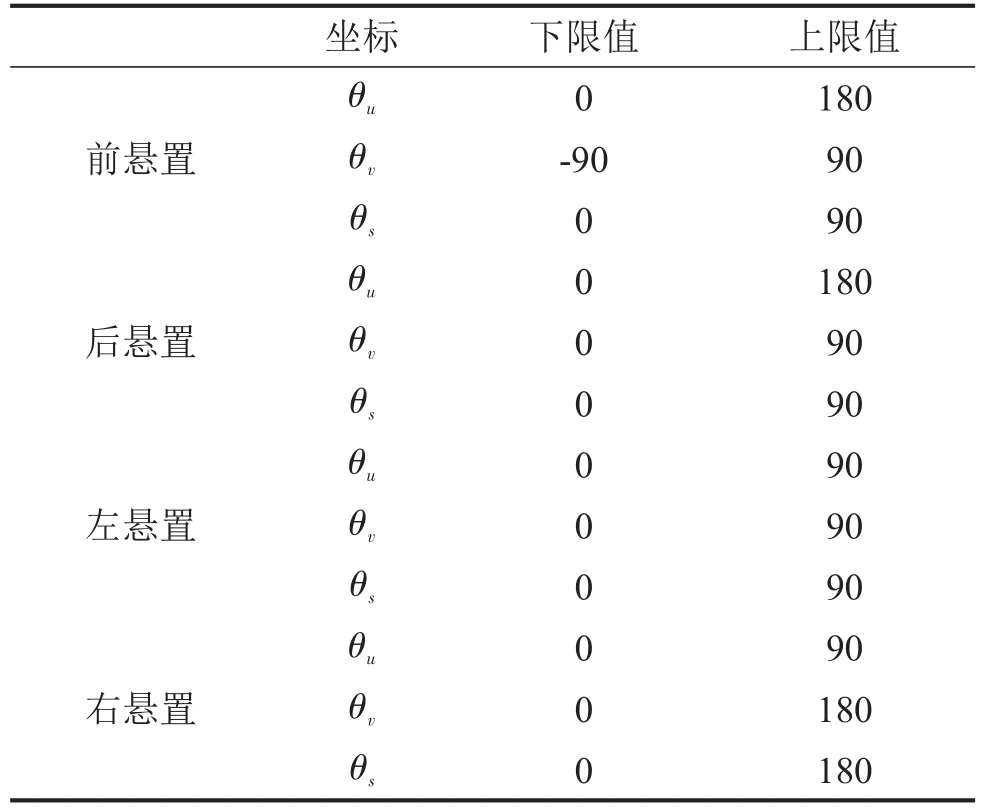
表7 懸置傾角約束范圍/(°)

優化后的剛度值，如表8。

傾斜角度，如表9。

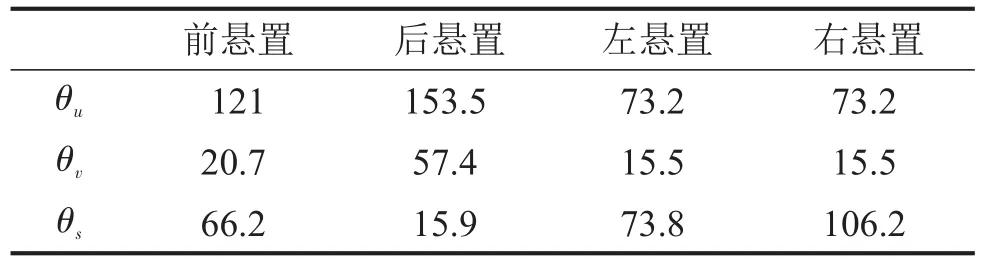
表9 優化后懸置傾角/(°)

固有頻率和解耦率(%)，如表10。

表10 優化后頻率和解耦率/(%)

5 結語

從優化結果可以看出，頻率分布比較均勻，且都大于5 Hz，避免與路面激勵產生共振，各個固有頻率的分布相隔大于1 Hz，更好的避免在設計中與其他系統產生干涉，提高系統的可靠性。解耦率的分布保證了在某一方向上占優，并且各個方向上的解耦率都大于80%，避免各個方向振動的相互耦合，提高了整車的舒適性。經過實車驗證，發現在怠速運轉情況下，方向盤抖動消失，驗證了優化結果具有可行性，具有一定的工程應用價值。

[1]時培成，李文江，丁芳.基于振動傳遞率和能量解耦率的懸置系統優化[J].汽車工程，2009，26(2)：1057-1060.

[2]龐劍，諶剛，何華.汽車噪聲與振動理論與應用[M].北京：北京理工大學出版社，2006.

[3]黃鼎友，吉向東.動力總成懸置系統建模及振動仿真[J].江蘇大學學報，2005，26（3）：222-223.

[4]陳達亮.動力總成懸置系統怠速隔振優化策略研究[J].噪聲與振動控制，2011（05）：54-55.

[5]呂振華，梁偉，上官文斌.汽車發動機液阻懸置動特性仿真與實驗分析[J].汽車工程2002（24）：105-106.

[6]李楠.動力總成懸置系統優化與仿真分析[J].重慶交通大學學報，2012，31(1)：125-127.

[7]李玉桂.動力總成懸置系統的布置設計與解耦優化[J].機電技術，2012(1)：49-51.

[8]李濤，賀勇軍，劉志儉.等編著.Matlab工具箱應用指南—應用數學篇[M].北京：電子工業出版社，2000.

[9]陳蔭三，余強譯.汽車動力學[M].北京：清華大學出版社，2009.

[10]饒著，李欣業，張明路譯.機械振動[M].北京：清華大學出版社，2009.

[11]沈志宏，郭福祥，基于能量解耦法的動力總成懸置系統優化設計[J].噪聲與振動控制，2010（03）：35-37.

[12]梁天也，史文庫.發動機懸置研究綜述[J].噪聲與振動控制，2007（01）：6-9.

Decoupling and Optimal Design of a Powertrain Mount System Based on Matlab

XUE Hua1,LIU Zhi-qiang1,LIU Yan2,SU Ying2
(1.College of Mechanical Engineering,Liaoning Technical University,Fuxin 123000,Liaoning China; 2.BrillianceAuto Engineering Research Institute,Shenyang 110000,China)

It is known that powertrain mount system plays an important role in vehicle design.For the steering wheel of a car shaking violently in the idle condition,its powertrain and suspension parameters were measured,and a 6-DOF mathematical model of the powertrain mount system was established.The decoupling analysis showed that the coupling effect was serious in all the directions.Therefore,system optimal design was done.Firstly,the mount position was adjusted based on the impact center theory.Then,choosing the rigidity of the mount system and the mount inclination angle as the constraint variables and the minimum decoupling of the 6 directions as the objective function,the optimal design was done using the multi-objective optimization function“fgoalattain”of the Matlab.The results show that this method can realize better decoupling in all directions within a certain range of constraints and has high practical application values.

vibration and wave;powertrain;mounting system;idle vibration;multi-objective optimization;energy decoupling

U461.4

A

10.3969/j.issn.1006-1335.2015.02.016

1006-1355(2015)02-0065-04

2014－08－06

薛華（1960－），男，副教授，碩士生導師，研究方向：工礦車輛的可靠性與故障診斷。E-mail:xuehua601229@126.com

劉志強（1986－），男，內蒙古呼和浩特人，碩士生，主要研究方向：動力總成及整車振動控制研究。

發動機作為整車的動力裝置，對于整車的振動和聲學性能的影響具有重要的作用，也就是通常所說的NVH特性。隨著技術進步以及道路條件的改善，作為車輛動力裝置的發動機成為主要噪聲源。NVH性能的優劣，直接決定了整車在市場當中的占有率。在最近的幾十年中，消費者對汽車的舒適性提出了更高的要求，作為汽車的生產廠家，為了提高市場的認可度，在滿足法規和成本要求的前提下，都在盡可能生產出市場認可的產品。目前在高端車市場上較多的采用了主動懸置和半主動懸置來提高整車使用性能，作為在傳統車型中較多使用的橡膠懸置，由于其較高的可靠性和低成本，一直備受汽車廠家的青睞[1，2，12]。