改進粒子群算法的PID神經網絡解耦控制

于立君，陳佳，劉繁明，王輝

（哈爾濱工程大學自動化學院，黑龍江哈爾濱150001）

改進粒子群算法的PID神經網絡解耦控制

于立君，陳佳，劉繁明，王輝

（哈爾濱工程大學自動化學院，黑龍江哈爾濱150001）

綜合減搖控制系統存在非線性、多變量、強耦合等因素，會導致減搖系統達不到最佳控制狀態。利用粒子群算法具有對整個空間進行高效搜索以及PID神經網絡的自適應特點，提出一種改進粒子群算法，以解決粒子群算法中存在算法精度不高、粒子易陷入局部極小值等問題，并提高PID神經網絡訓練速度和訓練精度，便于參數尋優。仿真結果表明，改進的粒子群算法具有一定優越性，將其運用到綜合減搖控制系統解耦控制器設計中，能夠有效地減小船舶橫搖，達到較好的控制效果。

粒子群算法；綜合減搖系統；PID神經網絡；解耦控制；仿真分析

綜合減搖控制系統具有非線性強、控制變量多、耦合性強、結構復雜且時變等特點［1］，這些因素的存在使得傳統控制器在系統應用中有一定的局限性，其應用的有效性也會受到很大的限制。因此，選擇合理的解耦控制算法并有效地應用到控制器設計中［2］，將在很大程度上提高多變量耦合系統的控制效果。近年來，由于粒子群算法具有易實現、通用性強、收斂速度快等特點，被廣泛應用到各個領域中［3?5］。同時針對標準粒子群算法存在的缺陷，為了提高粒子群算法的性能，國內外研究學者在算法的慣性權重、加速度系數因子等方面提出了許多改進方法。胡建秀等［6］提出了一種線性微分遞減策略方法，用以提高算法的收斂速度。但是該算法會在迭代過程中出現進入局部極值區域就難以跳出的問題。陳水利等［7］提出了一種非線性調整加速度系數因子的策略，可使算法以最快速度搜索到最優解所在的區域。經過驗證該方法能夠得到較理想的效果，但是由于后期種群的多樣性的喪失，容易造成早熟收斂。Alireza［8］在傳統粒子群優化方法的基礎上提出了具有適應變異機制和動態慣性權重系數的算法，以增強算法的全局搜索能力，并提高準確性。算法對動態權重的慣性系數進行了改進，卻沒考慮加速度因子對算法的影響。本文針對上述改進粒子群算法中仍然存在的問題，提出了一種新的改進時變加速度系數的粒子群算法，將該算法與標準粒子群算法進行比較，并應用到綜合減搖控制系統解耦控制器設計中，驗證了改進算法的有效性。

1 綜合減搖耦合系統數學模型分析

綜合減搖控制系統中，當橫搖角較小時，可以把船舶—減搖水艙系統看作是一個受激勵的二自由度振動系統，把減搖鰭的扶正力矩Kc＝A?＋B?·＋C?¨引入到該系統，可以建立綜合減搖系統運動的微分方程［9?10］：

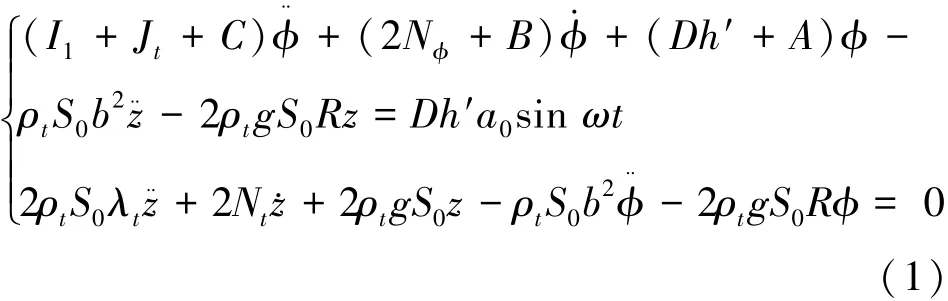
式中：I1＝I＋ΔI，I和ΔI分別為相對于過船舶重心的縱軸慣量和附加慣量；2N?為船舶阻尼力矩；D為排水量；h′為穩心高；S0為邊艙自由液面面積；S為沿水艙軸線的法線方向的局部截面積；r為微質量dm的質心到橫搖軸的距離；γ為r與d之間的夾角；dl為液體微體積沿水艙軸線的長度；l為型水艙軸線長度；為艙內水柱相當長度；b2＝為水艙軸線對橫搖軸的靜壓力矩；Jt＝為艙內液體對橫搖軸的質量慣性矩；R為邊艙中至船舶縱中刨面的水平距離；N?為船舶阻尼系數；ρt為海水密度；V為航速；Af為鰭的投影面積；?Cy／?α為升力系數斜率；

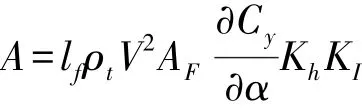
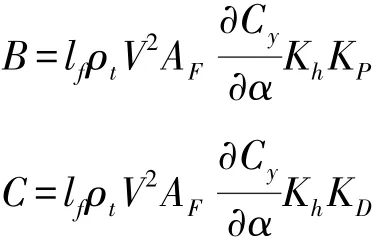
對式（1）進行無量綱化可得

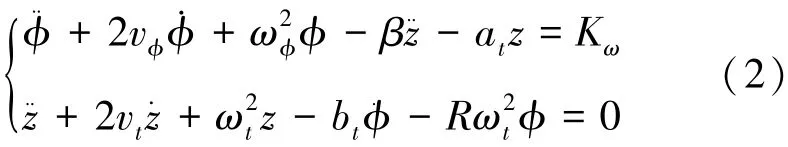
由式（2）可以看出綜合減搖控制系統中存在著耦合項，而這種耦合影響是由船舶橫搖角?及它的二階導數?¨所引起的。因此，需要選取合適的控制算法對系統進行解耦控制，進而消除減搖系統中存在的耦合影響，達到提高綜合減搖系統性能的目的。

2 改進粒子群算法的PID神經網絡解耦控制

2．1 改進粒子群算法

改進粒子群算法分析步驟如下。

粒子群的進化方程［11］可描述為

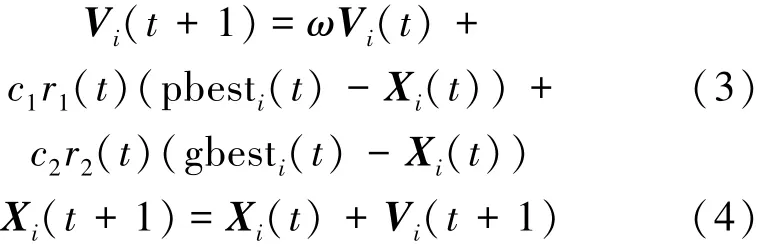
式中：ω為慣性權重，描述的是粒子上一次運行速度對當前次運行速度的影響［12］。Vi（t）表示第i個粒子在第t次迭代過程中的速度矢量，Xi（t）表示第i個粒子在第t次迭代過程中的位置矢量，pbesti（t）、gbesti（t）分別代表第i個粒子在第t次迭代后該粒子的歷史最優點和種群歷史最優點。方程中參數t為迭代次數，r1、r2為［0，1］的隨機數，用來保持種群個體的多樣性［13］。c1、c2為加速度系數因子，可以使粒子向自己的歷史最優點和種群歷史最優點靠近，通常取值在0～4之間。

Ratnaweera等［14］、喬俊飛等［15］提出了一種參數自調整策略，在進化過程中，通過調整加速度系數動態調節算法的局部和全局搜索能力。對于時變加速度系數，調節公式定義如下：

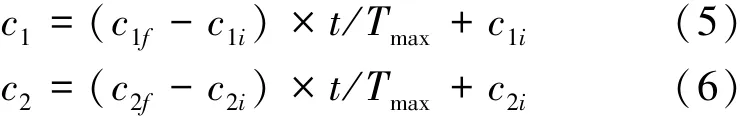
式中：c1i、c1f、c2i和c2f均為常數，t是當前的迭代次數，Tmax是最大的迭代次數。

本文在此基礎上做如下修改，提出一種改進的時變加速度系數的粒子群算法，定義加速度系數公式如下：

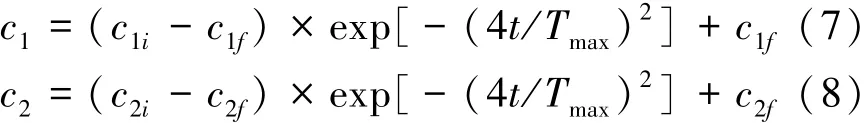
式中：c1i和c2i分別是加速度系數c1和c2的初始值。c1f和c2f分別是加速度系數c1和c2的最終值。則改變加速度系數后，粒子群算法更新方程如下：

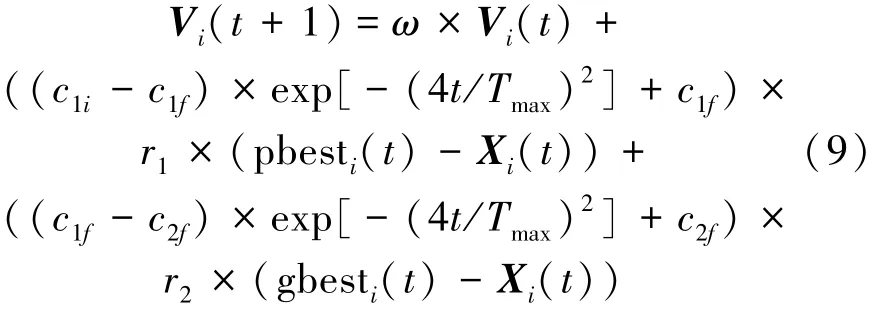
改進粒子群算法流程如圖1所示。

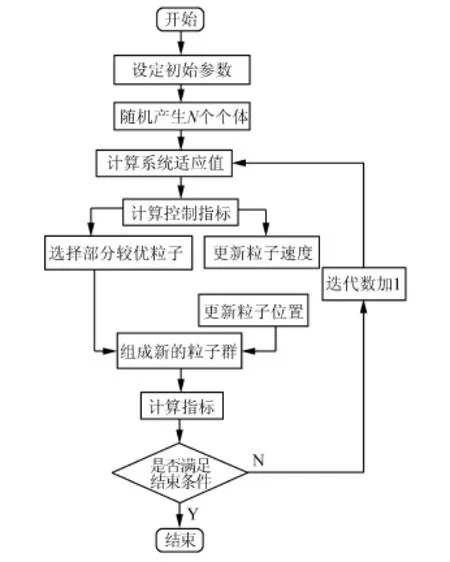
圖1 改進粒子群算法流程Fig．1 The flow chart of improved PSO algorithm

2．2 改進粒子群算法的綜合減搖系統PID神經網絡解耦控制

選取式（2）為綜合減搖系統模型進行分析，相應的系統參數如表1所示，并對式（2）進行變換得

對式（10）進行Laplace變換并整理可得

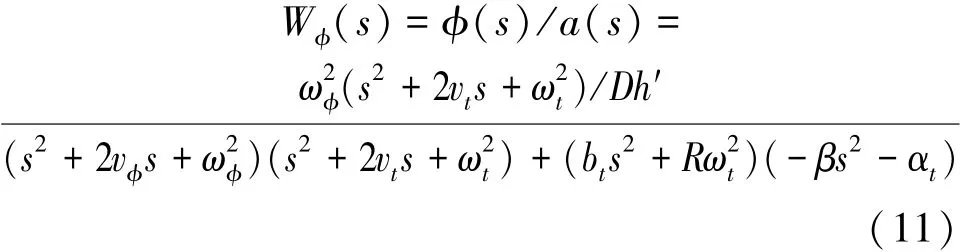
根據表1中的數據可以得到該減搖系統具體表達式為

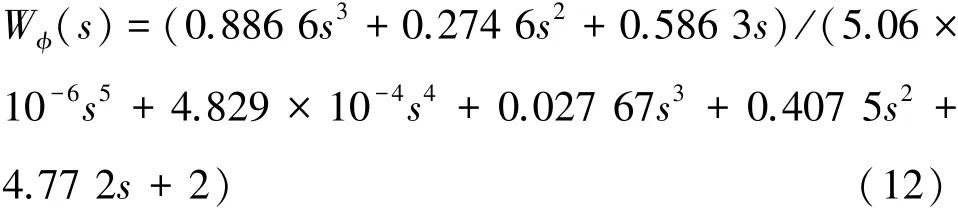
本文選取綜合減搖控制系統性能指標函數為

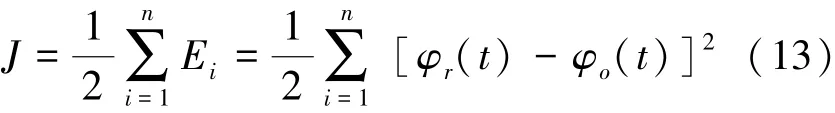
式中：Ei為輸出橫搖角的誤差平方和，φr（t）為預測輸出橫搖角，φo（t）為實際輸出橫搖角，n為訓練樣本數。粒子群中個體的適應度函數選為

表1 綜合減搖系統主要參數Table 1 Parameters of integrated stabilization system

3 仿真分析

為了驗證本文提出的改進粒子群算法的可行性以及優劣性，分別采用標準粒子群算法和改進粒子群算法對式（14）中的適應度函數進行仿真，并從收斂速度、最優適應度值的變化情況以及搜索精度3方面進行比較。選取相應的參數為：初始關系權重ωmax＝0．9，終慣性權重ωmin＝0．1，最大速度量Vmax＝0．03，最小速度量Vmin＝－0．03。

選取種群規模為m＝100，迭代次數為40進行仿真，結果如圖2～6所示。

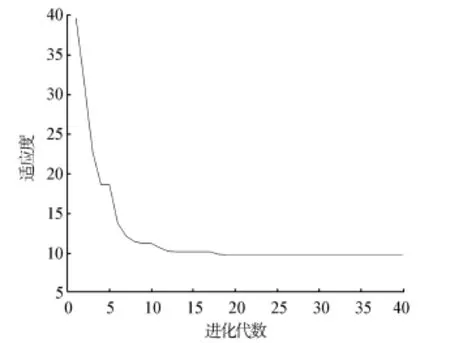
圖2 標準粒子群算法適應度曲線Fig．2 The fitness curve of standard PSO algorithm

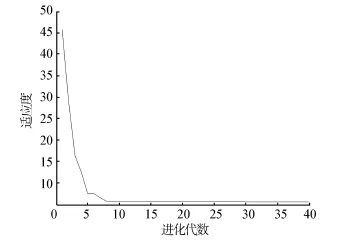
圖3 改進粒子群算法適應度曲線Fig．3 The fitness curve of improved PSO algorithm

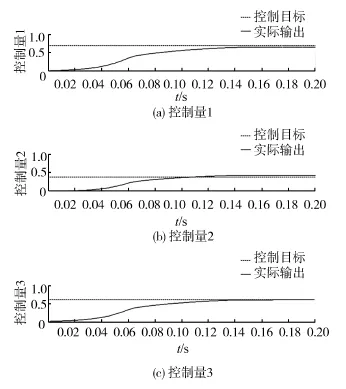
圖4 傳統PID神經網絡控制圖Fig．4 Neural network control chart of traditional PID

圖5 基于改進粒子群算法的PID神經網絡控制圖Fig．5 Neural network control chart of improved parti?cle swarm optimization PID

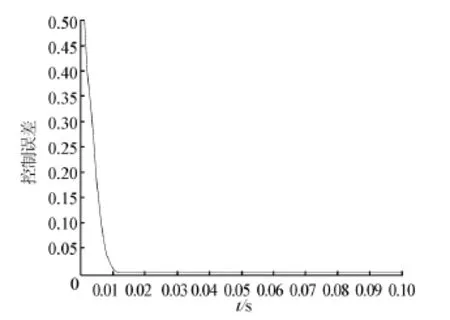
圖6 改進粒子群算法控制誤差曲線Fig．6 The control error curve of improved PSO algorithm

圖2～3分別為改進粒子群算法和標準粒子群算法對適應度函數尋優時的適應度曲線。可以看出，改進的粒子群算法在對適應度函數尋優過程中有較高的收斂速度和較好的收斂性，這也為改進粒子群算法在綜合減搖控制系統PID神經網絡解耦控制器設計中的應用提供了可行性。

由圖4～6可以看出，改進粒子群算法優化后的PID神經網絡可以取得較好的控制效果，控制量能夠迅速逼近控制目標，響應時間也相對縮短。

選取特定航速為18 kn，有義波高為3．3 m，遭遇角為90°時，對2種不同算法控制下系統橫搖角進行仿真，結果如圖7～8所示。

圖7 標準粒子群算法下綜合減搖系統橫搖角Fig．7 Roll angle under the standard PSO algorithm

圖8 改進粒子群算法解耦后綜合減搖系統橫搖角Fig．8 Roll angle under the improved PSO algorithm

對比圖7、8可以看出，采用改進粒子群算法優化PID神經網絡設計出的解耦控制器，其減搖效果優于傳統的標準粒子群算法。為了驗證基于改進粒子群算法設計出的PID神經網絡解耦控制器在綜合減搖控制系統中的應用效果不失一般性，選取不同情況下的參數對該方法進行仿真驗證，可得到仿真數據如表2所示。

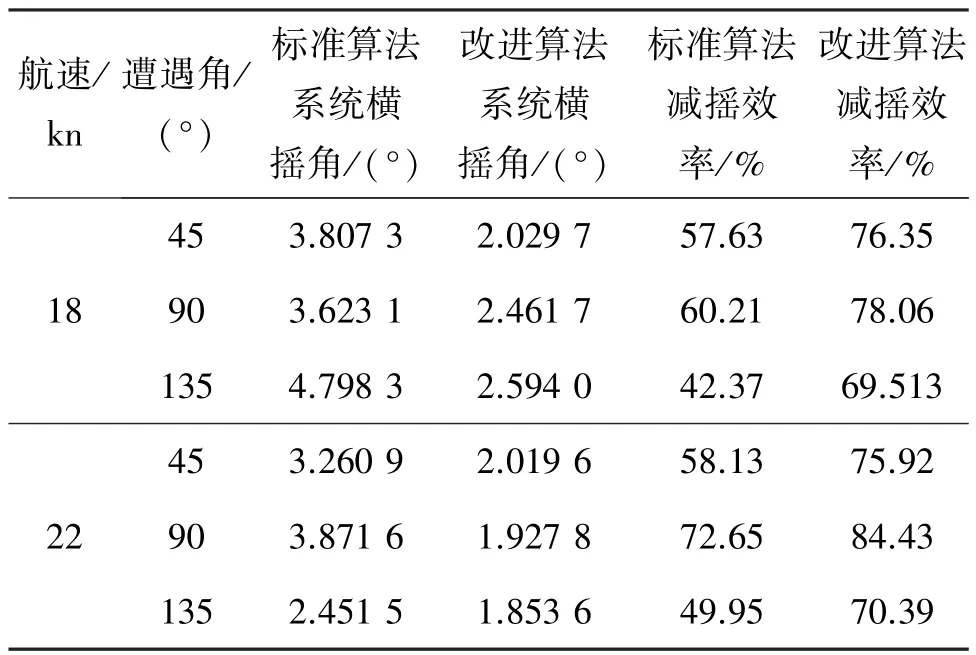
表2 不同控制方法的仿真數據統計Table 2 Simulation statistics of different control methods

由表2可知，在選取特定的海情和航速下，采用改進的粒子群算法優化PID神經網絡控制器對系統進行控制，可以得到更小的橫搖角和更高的減搖效率。與標準粒子群算法優化PID神經網絡控制器相比，改進粒子群算法能夠有效地減小船舶橫搖角，取得較好的控制效果，提高控制系統的綜合減搖性能。

4 結束語

在建立綜合減搖系統耦合模型的過程中，為便于進行系統分析，通常會忽略耦合模型的復雜性和不確定性，這也給系統解耦帶來一定的影響。為提高系統的收斂速度和收斂精度，本文在標準粒子群算法的基礎上進行改進，采用改進粒子群算法進行PID神經網絡參數尋優。仿真結果表明，采用本文提出的改進粒子群算法優化PID神經網絡，進行解耦控制器設計能夠有效降低減搖控制系統中的耦合作用，減小船舶橫搖，取得較好的控制效果。

［1］孟祥振．綜合減搖系統參數配置及控制器優化研究［D］．哈爾濱：哈爾濱工程大學，2012：27?28．MENG Xiangzhen．The study of parameters configuration and controller optimization of integrated stabilization system［D］．Harbin：Harbin Engineering University，2012：27?28．

［2］周西峰，林瑩瑩，郭前崗．基于粒子群算法的PID神經網絡解耦控制［J］．計算機技術與發展，2013，23（9）：158?161．ZHOU Xifeng，LIN Yingying，GUO Qiangang．PID neural network decoupling control based on particle swarm optimi?zation［J］．Computer Technology and Development，2013，23（9）：158?161．

［3］MOHANDES M A．Modeling global solar radiation using particle swarm optimization（PSO）［J］．Solar Energy，2012，86（1）：3137?3145．

［4］應進．基于粒子群算法的航空發動機多變量控制研究［D］．南昌：南昌航空大學，2011：23?24．YING Jin．Multivariable control for aeroengines based on particle swarm optimization algorithm［D］．Nanchang：Nan?chang Hangkong University，2011：23?24．

［5］AL?GEELANI N A，PIAH M A M，ADZIS Z，et al．Hybrid regrouping PSO based wavelet neuralnetworks for character?ization of acoustic signalsdue to surface discharges on H．V．glass insulators［J］．Applied Soft Computing，2013，13（12）：4622?4632．

［6］胡建秀，曾建潮．微粒群算法中慣性權重的調整策略［J］．計算機工程，2007，33（11）：193?195．HU Jianxiu，ZENG Jianchao．Selection on inertia weight ofparticle swarm optimization［J］．Computer Engineering，2007，33（11）：193?195．

［7］陳水利，蔡國榕．PSO算法加速因子的非線性策略研究［J］．長江大學學報（自然版）：理工卷，2007，4（4）：1?4．CHEN Shuili，CAI Guorong．Nonlinear strategy of PSO algo?rithm acceleration factor［J］．Journal of Yangtze University（Nat Sci Edit）：Sci＆Eng V，2007，4（4）：1?4．

［8］ALIREZA A．PSO with adaptive mutation and inertia weight and its application in parameter estimation of dynamic sys?tems［J］．Acta Automatica Sinica，2011，37（5）：541?549．

［9］于立君，孟祥振，金宏章，等．綜合減搖系統參數配置研究［J］．中國造船，2012，53（4）：13?21．YU Lijun，MENG Xiangzhen，JIN Hongzhang，et al．Study of configuration parameters of integrated stabilization system［J］．Shipbuilding of China，2012，53（4）：13?21．

［10］于立君，孫經廣，劉繁明，等．廣義預測算法在綜合減搖系統控制器設計中的應用［J］．船舶工程，2013，35（6）：76?79，83．YU Lijun，SUN Jingguang，LIU Fanming，et al．Applica?tion of generalized prediction algorithm in designing inte?grated stabilization system controller［J］．Ship Engineer?ing，2013，35（6）：76?79，83．

［11］CHIOU J S，TSAI S H，LIU Mingtang．A PSO?based a?daptive fuzzy PID?controllers［J］．Simulation Modelling Practice and Theory，2012，26：49?59．

［12］沈錫．基于粒子群優化算法的船舶航向PID控制［D］．大連：大連海事大學，2011：6?7．SHEN Xi．PID control for ship steering based on particle swarm optimization［D］．Dalian：Dalian Maritime Universi?ty，2011：6?7．

［13］BOUALLèGUE S，HAGGèGE J，AYADI M，et al．PID－type fuzzy logic controller tuning based on particle swarm optimization［J］．Engineering Applications of Artificial In?telligence，2012，25（3）：484?493．

［14］RATNAWEERA A，HAIGAMUGE S K，WATSON H C．Self?organizing hierarchical particle swarm optimizer with time?varying acceleration coefficients［J］．IEEE Transac?tions on Evolutionary Compution，2004，8（3）：240?255．

［15］喬俊飛，逄澤芳，韓紅桂．基于改進粒子群算法的污水處理過程神經網絡優化控制［J］．智能系統學報，2012，7（5）：429?436．QIAO Junfei，PANG Zefang，HAN Honggui．Neural net?work optimal control for wastewater treatment process based on APSO［J］．CAAI Transactions on Intelligent Systems，2012，7（5）：429?436．

An improved particle swarm optimization for PID neural network decoupling control

YU Lijun，CHEN Jia，LIU Fanming，WANG Hui
（College of Automation，Harbin Engineering University，Harbin 150001，China）

The integrated ship stabilization system has nonlinear，multi?variable and strong coupling characteristics，which may hinder the system from reaching the best control state．An improved particle swarm algorithm is proposed based on the characteristics of particle swarm optimization（PSO）algorithm，which can search the parameter space efficiently，along with its associated PID artificial neuron network that has self?regulation and adaptability．The im?proved particle swarm algorithm can overcome disadvantages in former particle swarm algorithms such as low preci?sion，the particles tend to fall into extremely small values，and so on．In addition，the improved algorithm can in?crease the training speed and precision of the PID nerve network，which facilitates parameter optimization．The sim?ulation results show that the improved PSO has certain advantages，it can reduce ship rolling，and can achieve ex?cellent control effects when it is applied to the design of the decoupling control of an integrated stabilization control system．

particle swarm algorithms；integrate stabilization system；PID neural network；decoupling control；sim?ulation analysis

于立君，男，1975年生，副教授，博士，主要研究方向為船舶運動控制、先進控制理論及應用。主持并完成博士后基金1項、橫向項目1項、中央高校自由探索計劃5項，獲得黑龍江省科技進步二等獎1項。

陳佳，女，1989年生，碩士研究生，主要研究方向為船舶智能控制理論方法與應用。

劉繁明，男，1963年生，教授，博士生導師，主要研究方向為水下潛器定位技術、弱信號測量與處理技術、被動導航與定位技術、工業裝置測控技術。承擔“十二五”預先研究項目2項，國家自然科學基金重點項目1項，設備研制項目多項。

TH186

TP18

1673?4785（2015）05?0699?06

10．11992／tis．201406028

http：／／www．cnki．net／kcms／detail／23．1538．tp．20150930．1556．004．html

于立君，陳佳，劉繁明，等．改進粒子群算法的PID神經網絡解耦控制［J］．智能系統學報，2015，10（5）：699?704．

英文引用格式：YU Lijun，CHEN Jia，LIU Fanming，et al．An improved particle swarm optimization for PID neural network de?coupling control［J］．CAAI Transactions on Intelligent Systems，2015，10（5）：699?704．

2014?06?17．

日期：2015?09?30．

中央高校自由探索計劃資助項目（HEUCF041406）．

于立君．E?mail：yulijun＠hrbeu．edu．cn．