雙連梁的等效方法及其對比分析

■劉光輝，王艷晗 ■北京林業大學水土保持學院，北京 100083

所謂雙連梁即指將單根連梁以水平縫隔開而形成上下兩根連梁，是對超筋連梁的一種特殊處理手段［1］。鑒于目前的計算方法和計算軟件的限制，雙連梁在結構設計上還沒有一個成熟的計算方法，當前的計算方法是先將兩根連梁看成一個整體，進行計算內力，然后將內力平均分配給兩根梁，單獨進行配筋，這樣的做法，有一定的局限性，計算出的受力情況和配筋結果與實際情況有很大差別，這就需要我們尋找出一種能近似真實的表達出雙連梁的實際受力情況的等效方法。通過閱讀相關學者的文章，本文認為可以歸納為四種等效方式，即抗剪剛度等效(又稱簡單等效)、抗彎剛度等效、抗側移剛度等效、抗轉角剛度等效(最近天津大學提出的一種新思路)，本文就各種等效方法進行分析和比較，找到一個更加合理，更加近似于實際工程結構的等效方法。

1 幾種等效方法的介紹

1.1 抗剪剛度等效

所謂抗剪剛度等效，由于材料特性相同，即雙連梁的抗剪截面面積等效，又稱簡單等效，通俗地講，抗剪剛度等效就是指雙連梁截面高度減半，寬度加倍，它的優點是原則簡單，容易理解和配筋，表面上看，它的內力值似乎并未發生改變，然而真實情況是，梁截面的抗彎內力值卻發生了明顯的變化，這其實是一種相當不準確的等效。

1.2 抗彎剛度等效

對于抗彎剛度等效，顧名思義是截面的抗彎剛度模量相同，最終是轉動慣量I 相同，按近似方法計算，經過處理后的截面高度H=0.8h，而廣東省設計研究院的焦柯等人試算出了該等效方法的一般公式，得到了最后等效模型需要的剛度折減系數，H=0.76h［2］。

1.3 抗側移剛度等效

對于抗側移剛度等效的理解，筆者認為是通過計算機模擬加計算推導得出來的，先通過有限元分析軟件將雙連梁模型輸入進去，在墻肢端給以固定的荷載，求解出此時的最大位移，然后輸入一個單連梁模型，施加同一位置上的同樣的荷載，通過試算，往復調節連梁高度，使此時的最大位移與之前的雙連梁模型時的最大位移相等或者相近似，記錄出此時的連梁高度，此方法即抗側移剛度等效。

1.4 抗轉角剛度等效

最近，天津大學提出了一種新型的等效方法，并且推導出了它的相應的轉角等效公式，為雙連梁等效提出了一種新的思路。剪力墻結構中一個重要的系數是整體性系數α，其含義是連梁的各層轉角剛度與所有墻肢線剛度之和的比值再開平方，如果把雙連梁等效看成一根單連梁，結果是它相應的整體性系數就應該相同，這其中的實質是等效前后連梁對墻肢的約束能力相同，在線性分析中兩者一定會表現出相同的受力性能，對于前后的整體性系數相等，如果保持墻肢的各方面指標不變，自然變為等效前后連梁的轉角剛度相等，這就是抗轉角剛度等效［3］。

2 模型設計

為了研究雙連梁在幾種方法等效后的受力狀態和各種指標因素，我們在有限元軟件Ansys 中建立五個模型，墻肢長度統一為4.0m。第一個模型是水平開縫的雙連梁模型，單個墻肢的截面高度取2000mm，墻肢厚度取200mm，開縫尺寸為100mm，每根梁b ×h 是200 ×900，洞口寬度為1200mm，因此洞口高度為2100mm;第二個模型是抗剪剛度等效的模型，b × h 為200 × 1900mm，墻肢厚度取200mm，洞口寬度為1.2m，計算得出洞口高度是2100mm;第三個模型為抗彎剛度等效的模型，b×h 為200 ×1134mm，墻肢厚度取200mm，洞口寬度為1200mm，洞口高度為2866mm;;第四個模型為抗側移剛度等效的模型，根據朱炳寅先生的手算推導，b×h 為200 ×1460mm，墻肢厚度取200mm，洞口寬度為1200mm，洞口高度為2540mm;;最后一個模型為抗轉角剛度等效的模型，該等效思路比較新穎，經過計算，其b ×h 為200 ×1352mm，墻肢厚度取200mm，洞口寬度為1200mm，洞口高度為2648mm。

表1 各等效連梁截面尺寸

3 結果分析

用單元shell63 來模擬建立本文所列模型。在每個模型的頂部均施加大小為500KN、方向水平向右的集中力，并將兩片剪力墻下端設定為嵌固端，計算得Ansys 分析結果，分別對左截面梁端進行內力求解，可以得到左側截面的內力如下:

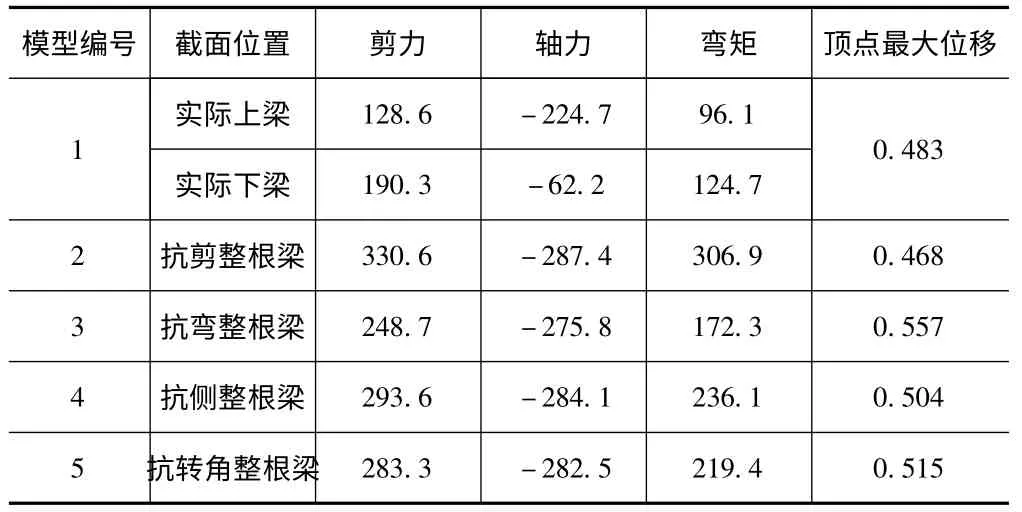
表2 五組等效連梁模型左截面內力及頂點最大位移

從上表不難看出，模型2 的剪力與實際情況模型1 最接近，這是因為兩種模型的抗剪截面即截面面積相差不是很大，在這之后，是模型4的剪力最為接近實際情況，然后是模型5，最后是模型3;對于軸力，幾種模型的軸力幾乎沒有多大變化，說明在一定等效范圍內，等效方法的不同對梁端的軸力影響不大，模型4 與實際情況最為接近;對于彎矩，模型4 和5 與實際情況較為接近，說明抗側移剛度等效和抗轉角剛度等效在計算配筋方面誤差小于其他方法，模型1 的彎矩與實際情況相差較大，這點在實際結構設計中對配筋有很大的影響，這也是抗剪切剛度等效被公認為誤差較大的最主要的原因，所以在這里無論在其他各項數據方面抗剪剛度等效與實際情況有多么的接近，我們首先先定義該方法為最不合理的方法;至于頂點最大位移，模型2 最為接近實際情況;接下來是模型4、5、模型3 即抗彎剛度等效與實際情況的最大位移相差最大。綜上可知，按抗側移剛度等效方案得到等效連梁在結構位移及內力各方面都與等效前的雙連梁吻合良好，可以嘗試對結構進行分析。

連梁超筋的本質是連梁剪壓比超限，抗剪截面面積不夠，連梁在水平地震作用下的剪壓比:

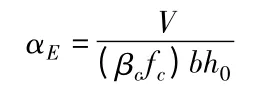
式中:αE為連梁在水平地震作用下截面的剪壓比;V 為連梁剪力設計值;fc 為混凝土軸心抗壓強度設計值;b 和h0分別為連梁截面寬度和有效高度;βc 為混凝土強度影響系數。如果把模型2 看成是初始結構，當連梁超筋時，設計人員為解決上述情況設計了在連梁中間設水平縫的模型1，在這里，對于模型1 和2 我們近似的認為他們的h0相等(忽略開縫，近似認為單梁有效高度為雙梁有效高度之和)，由上式可以看出，由于βc、fc、b 均不變因此αE只與V/H0的比值有關。實際上連梁剪力V 的變化與連梁高度、連梁的跨高比以及連梁與墻肢的線剛度比等各方面因素有關，是一個十分復雜的問題。

V/h0比值表3

從上面的表中，可以直接看出，模型2 的剪壓比與實際情況最為接近，但由于模型2 所對應的抗剪剛度等效的方法最為不準確，所以這里我們只拿模型3、4、5 與實際請情況比較，通過對比，我們可以很清晰的得出結論，三種情況模型4 最為接近、模型5 次之、模型3 最后。

4 結論

(1)抗剪剛度等效的思路得出的結果和現實模型存在著明顯的不同，沒有通過深入研究驗證，最好不要在結構設計中推廣。(2)通過閱讀大量文獻資料，針對各種雙連梁等效方法，筆者發現有個別文章對于抗彎剛度等效和抗側移剛度等效存在混淆分不清的問題，在這里筆者認為在個別文獻中我們常說的相對合理的等效方式“抗彎剛度等效”應該改為“抗側移剛度等效”，而“抗彎剛度等效”從字面上來看應該是本文中所說的EI 前后相等。(3)抗轉角剛度等效方法作為近幾年一種比較新穎的等效方法在各項指標上與抗側移剛度等效較為接近，值得進一步分析和研究。

［1］朱炳寅.對“雙連梁”的認識與設計建議［J］.建筑結構技術通訊，2008，11.

［2］陳云濤.雙連梁的等效分析［J］.建筑結構，2011(S1).

［3］姜忻良，宣波.剪力墻結構中雙連梁的轉角剛度等效方法［J］.建筑結構，2013(S2).