網格錨定單體碟形網箱的水動力特性研究

徐為兵, 朱克強, 張大朋, 楊然哲

(寧波大學 海運學院, 浙江 寧波 315211)

過度捕撈和近海海洋環境污染導致近岸海洋漁業資源枯竭。發展創新型漁業, 大力調整漁業產業結構, 轉變漁業經濟的增長方式是我國漁業的政策導向。深水抗風浪網箱是全球沿海國家開發海洋經濟的重要戰略裝備, 也是我國新時期現代農業向海洋領域拓展的重要戰略需要。我國深水網箱養殖事業起步比較晚, 與挪威、美國、日本等國在深水養殖領域存在相當差距。目前綜合各方面因素來看, 結構形式較為簡單、管理較為方便而且價格較低廉的重力式網箱更適合我國的國情, 全國絕大多數采用的都是此類網箱。張雅芝[1-2]等從水產養殖的角度分析了我國海水網箱養殖長久以來存在的各種問題, 如網箱的布局、管理和魚類病害等, 這些問題制約著我國網箱養殖的發展。但是如果能在認識這些問題的基礎上, 加強對海水養殖容量的研究, 開發優良品種,保護種質資源并加強養殖水環境保護和病蟲防護,就能實現網箱養殖的可持續健康發展； 徐君義等[3]根據實際試驗海區網箱養殖的成果, 針對網箱的材料、魚種的選擇與運輸, 總結出了實際養殖過程中發現的一些經驗； 王福表[4-5]則專門分析了網箱養殖水域污染源的成因和特點, 并根據實際考察給出了水污染治理的一些相關對策。同時, 作者針對網箱的有機質淤積帶來的危害, 研制了一種在沉降物未到達水底前就能被收集清除的新型網箱。雖然目前浮式重力式網箱應用較廣, 但它在強水流作用下, 網衣水平漂移嚴重, 網箱容積損失率高, 而加載保持網型的同時, 會使網衣承受的張力增加, 容易造成網衣撕破。因此, 在流速較大海域中, 該網箱的使用受到限制[6]。可見, 對先進網箱的了解和研究是必不可少的, 比較典型的為美國式鋼質升降式大型深水網箱, 國內也稱之為飛碟型可潛式大型深水網箱。國內外有關圓形重力式網箱數值模擬和模型實驗的研究成果比較豐富, 而目前為止國內對于碟形網箱只有較為詳盡的結構介紹和初步的水動力估算[6-10], 孫滿昌等[11], 李玉成等[12-13]對碟形網箱也僅僅是進行了模型實驗方面的研究。本文基于凝集參數法, 運用 OrcaFlex建立碟形網箱模型,通過數值模擬研究波流聯合作用下碟形網箱的纜繩受力特性和網箱結構的運動響應, 以期深入了解碟形網箱的水動力特性, 為碟形網箱及其錨泊系統的研究提供參考。

1 數值模型

本文研究的對象為沉降式碟形網箱。該網箱為一個自張緊結構, 主要由一個八邊形浮環和一個中心立柱組成。網箱浮環由8個鋼管分段用法蘭連接,每個分段分別密封并加壓。立柱和浮環的材料均為鍍鋅鋼, 用16根輻繩連接。中心立柱直徑為0.92 m,長9.14 m, 浮環的公稱直徑為15 m, 單根浮環管徑為27.3 mm, 輻繩材質為聚乙烯, 直徑13 mm。網箱用重達3 t的混凝土塊壓載, 通過懸掛索懸掛在中心立柱下面, 使之保證一定的穩性。中心立柱內有一個長達 3 m的體積可變的浮艙, 配合一定長度的懸掛索能使網箱下潛到特定的深度。網箱及錨泊系統的具體尺寸及浮標與網箱連接細節見參考文獻[14-15]。本文利用基于凝集參數法的專業水動力分析軟件OrcaFlex建立真實的網箱模型, 如圖1所示。有關凝集質量法的理論可見朱克強等[16-18]的研究, 在此不再詳細介紹。由于本文研究的主要內容是網箱整體和錨泊系統的水動力響應, 因此對網箱各種構件之間復雜的連接作了必要的簡化, 如繩索之間的連接全部簡化為鉸接。同時為了節省計算時間, 本文沒有真實模擬網衣受力, 并選用工程上常用的 Airy波理論和均勻流進行各種組合來對網箱養殖系統施加不同的環境載荷, 通過時域模擬后得到了不同載荷下的網箱水動力結果, 結合水動力分析結果給出了深海網箱在布錨過程中應注意的事項, 對實際工程實踐有一定的指導作用。

建模主要的思想是將整個網箱結構分割成受外力作用的若干個單元, 然后將外力平均分配到每個對應的節點, 形成一系列的運動方程。為了初步規劃和設計, 我們應用修改后的 Morison方程(公式(1)),來計算作用在籠狀結構小部件上的波浪力。

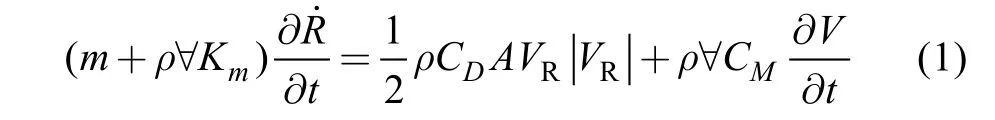
其中,m表示水質點的質量,ρ是海水的密度,Km是附加質量系數,CD是曳力系數,CM是慣性系數,A是投影面積, ?是網箱系統小部件排開水的體積,并且VR=V-R˙, 是水粒子速度V相對于結構速度R˙。公式(1)右邊的第一項通常認為是曳力, 而第二項稱為慣性力。所有的這些力是由一個受到海洋環境負載的移動物體激發的。不過, 當處理一個特定的單元時, 其他外部力, 如浮力、物重、和錨繩或網線伸長時產生的張力, 計算時都應包括在內。因此, 由牛頓第二定律可得, 公式(1)可以表示為：

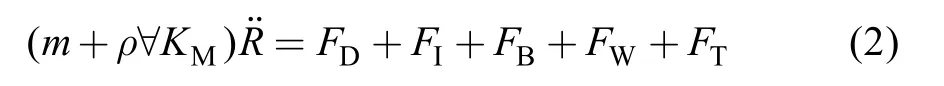
其中FD是阻力,FI的慣性力,FB浮力,FW是重力,FT是張力。

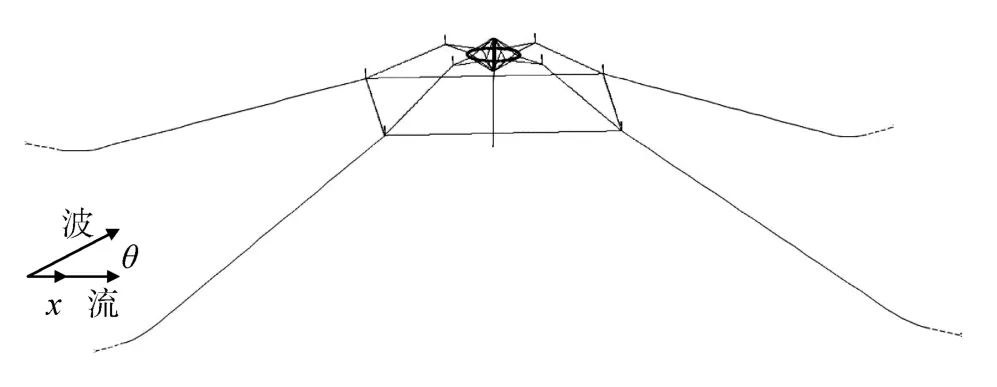
圖1 網箱模型示意圖Fig. 1 The model of the sea station

本文在建模過程中做了相應的處理, 如網箱中作為加強筋的輻繩之間并沒有網衣, 因此網箱整體受到的水動力有所減少, 但本文探究的是網箱系統整體的運動規律, 對網衣細節的模擬有待后續進一步的研究。八邊形浮環之間通過6D浮標相連, 為了確保浮環作為一個整體參與水動力計算, 浮環之間的端部的強度設為無限大。浮標在此只是起到連接作用, 并不參與水動力計算。軟件中對細長型結構均采用凝集質量模型, 該方法不僅計算速度快, 還具有較高的計算精度, 已經得到廣泛認可, 因此本文網箱系統模型中計算得到的錨泊張力具有一定的合理性。

2 算例分析

在深海區域, 常常會遇到臺風等惡劣天氣, 波浪和海流會同時出現, 錨泊系統將限制網箱的運動,保證網箱結構和魚群的安全。在波流聯合作用下, 網箱錨繩的受力將在一定程度上反映網箱整體結構的受力。一旦錨泊系統失效, 不僅會造成魚群逃逸和死亡, 還會對網箱結構造成嚴重破壞, 給養殖者帶來巨大的經濟損失, 因此研究錨泊系統的安全性是很有必要的。

本文研究在水深為55 m的深海中, 各種波流組合對網箱系統的作用, 包括3個波高(2、4、6 m)和3個周期(6、9、12 s)以及 4 種流速(0～2 m/s)[19]。需要注意的是, 軟件中默認的波流前進方向均為 180°(圖中所示海流流向為0°)。圖2顯示的是在純波作用下,迎流面錨繩上的最大張力與波浪周期和波高H之間的關系。由圖可知, 周期相同時, 純波作用下的錨繩張力均與波高大致呈線性關系； 波高一定時, 錨繩的張力隨周期的變化并不明顯, 且周期越大, 錨繩張力的幾乎保持不變。

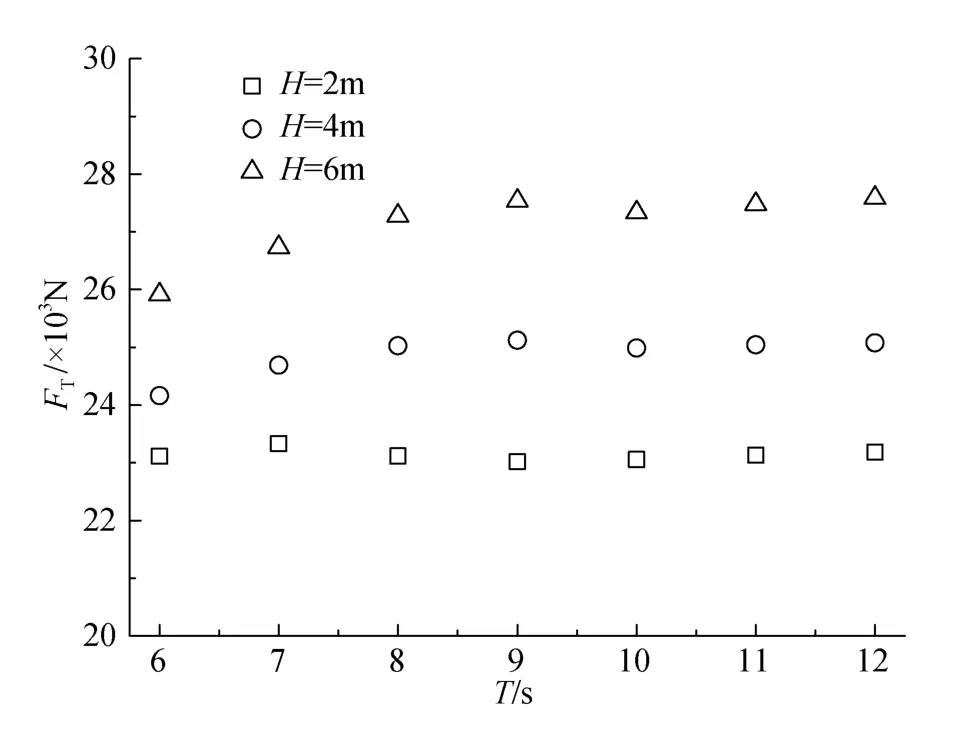
圖2 錨繩張力隨周期的變化Fig. 2 Changes of mooring line tension in various periods

圖3顯示了單個網箱系統在各種波流聯合作用下時迎流面錨繩張力的最大值。由圖3a～圖3c可知,波浪周期較長, 流速相同時, 相同波高作用下的網箱錨繩張力的最大值幾乎相同； 當波浪周期一定時(圖 3d～圖 3f), 波高越大, 網箱系統的錨繩張力最大值也越大； 且隨著流速的均勻增加, 錨繩張力最大值并不是線性增加, 而是呈現出增幅越來越快的趨勢。波浪周期越小, 流速越大, 水粒子的水平方向的合速度就越大, 由公式(1)可知, 網箱系統受到的水動力就越大, 波浪的波高越大, 水粒子的垂直方向上的速度就越大, 水動力也同樣會增大。

綜合對比以上各圖可以發現, 在本文的研究中,波流參數對網箱錨繩最大張力影響的重要程度依次為： 流速V, 波高H, 周期T。

對于沉降式碟形網箱來說, 遇到臺風等惡劣天氣時迅速下沉到海底是保證網箱結構安全完整的重要手段。因此研究極限海況下網箱下沉時的受力情況也很有必要。深海中的波浪和海流前進的方向并不總是相同, 為了研究斜入射波和海流對錨繩張力的影響, 我們假設均勻流流只沿著x軸正方向運動,但波浪入射的角度不同。

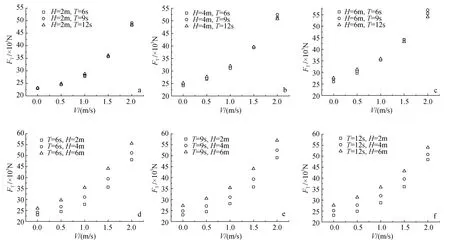
圖3 碟形網箱系統在不同波流狀態下的錨繩最大張力Fig. 3 The maximum mooring line tension induced by various wave-current conditions

圖4是在均勻流速為1.5 m/s時, 迎流面錨繩最大張力與入射波(H=6 m,T=9 s)前進角度的關系。從圖中可以看出, 錨繩的最大張力隨著入射波角度的變化呈周期性變化； 波流同向時要比波流逆向時的錨繩張力要大, 但最大張力發生在波流夾角為 135°左右的情況下, 與前人研究的結果相符； 而且從圖中可以看出, 網箱下沉能明顯地減少錨繩的受力,在本例中網箱下沉能使錨繩受力減少35%～43%。當波流夾角為 135°時, 在波浪前進的方向上 1#纜繩承受網箱整體受到的波浪力最大, 因此表現為此時 1#纜繩上的錨泊張力最大。本例計算得到的結果可以指導養殖戶在特定海洋環境下合理布置網箱的錨泊位置, 避免出現最大錨繩張力情況, 間接提高深海網箱系統的安全性, 減少不必要的損失。

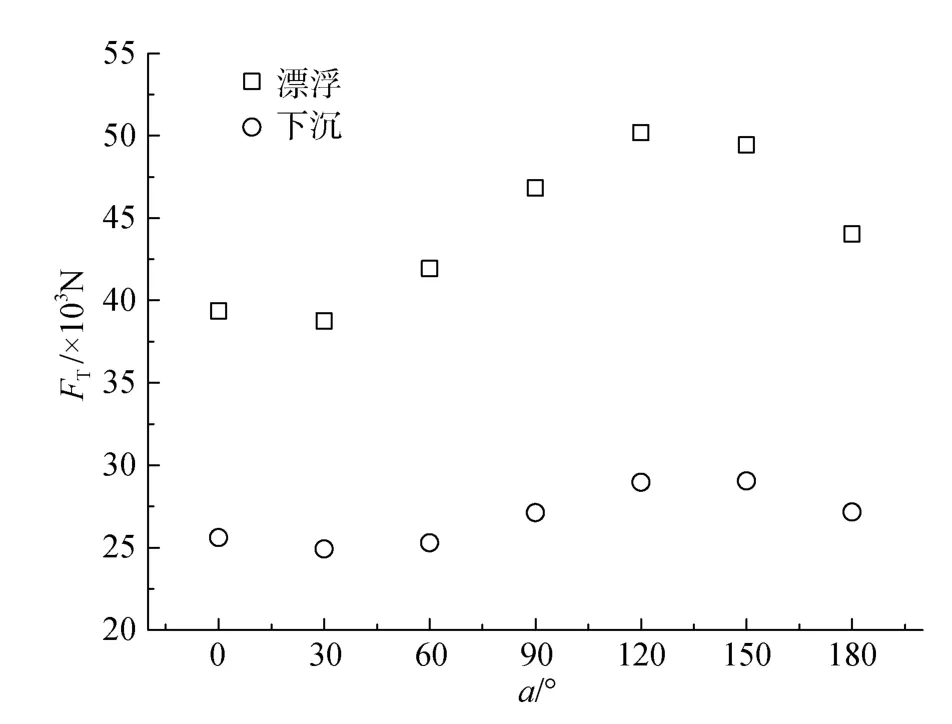
圖4 錨繩張力隨入射波角度的變化Fig. 4 The maximum mooring line tension induced by various incident angles of waves

如圖 5所示, 取浮環兩側中點 A、B, 假設浮環在波流聯合作用下發生的轉動和變形幅度很小, 則浮環整體的傾角可以通過A、B兩點的連線與水平線之間的夾角θ來表示。本文計算了不同波流作用情況下網箱漂浮時的浮環最大傾角, 如圖6所示。

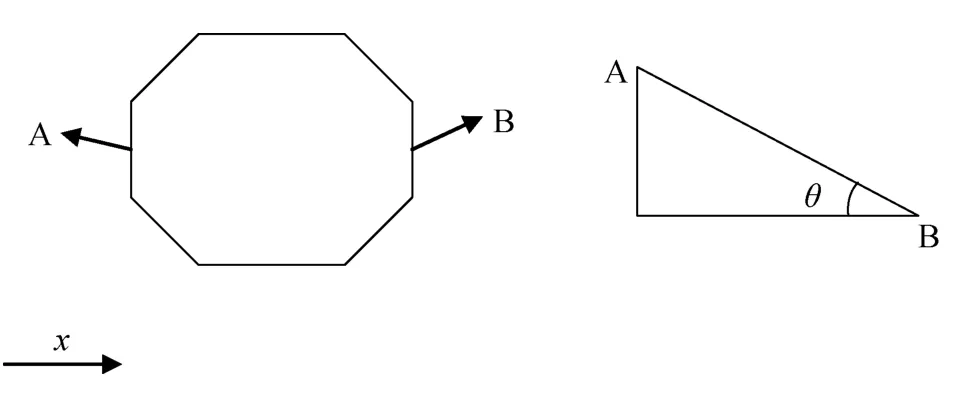
圖5 浮環傾角計算示意圖Fig. 5 The inclination calculation diagram of floating ring

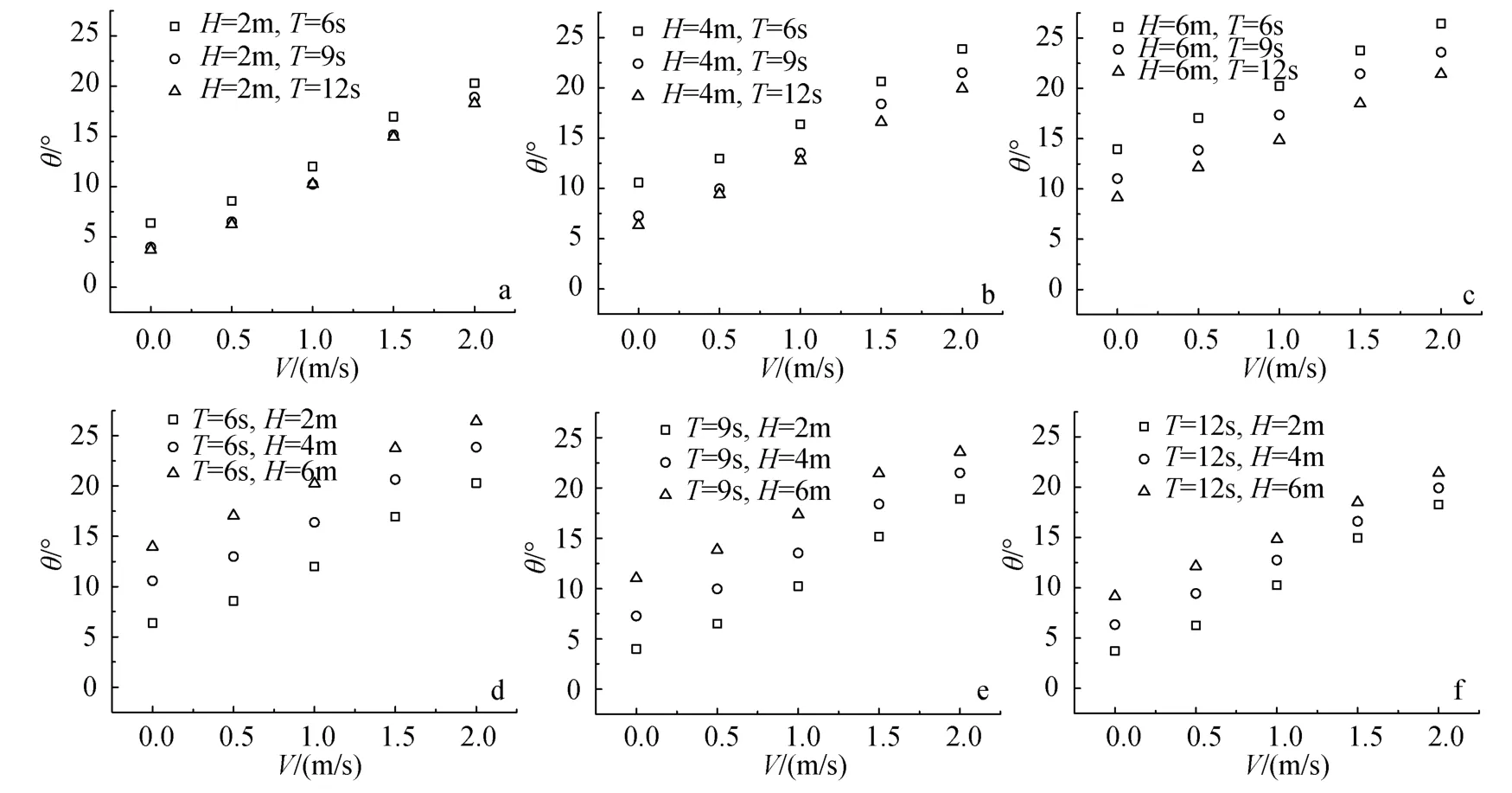
圖6 碟形網箱系統在不同波流狀態下的浮環最大傾角Fig. 6 The maximum inclination induced by various wave-currents

由圖 6a～圖 6c可知, 波高一定時, 浮環的傾角與流速大致呈線性關系。周期較小時(6 s), 浮環傾角會明顯較大； 相同流速下, 周期較大(9 s和12 s)、波高較小時(2 m和4 m)浮環傾角的差值很小, 但這個差值會隨著流速的增加而逐漸變大。由圖6d圖6f可知, 周期一定時, 浮環傾角和流速呈線性關系, 隨著波高的增加而增大, 但增大的幅度隨著流速和周期的增加而減小。

3 結語

純波作用下, 波浪周期相同時, 錨繩張力隨波高線性增加； 波高一定時, 錨繩張力隨周期的變化并不明顯, 且隨著周期越來越大, 錨繩張力趨于不變。

波流聯合作用下, 波浪周期較長時, 錨繩的最大張力幾乎相同； 當波浪周期一定時, 波高越大, 錨繩最大張力也越大, 且流速越大, 錨繩最大張力隨波高增加的幅度越小。波流參數對網箱錨繩最大張力影響的重要程度依次為： 流速V、波高H、周期T。

海流方向一定時, 錨繩最大張力隨波浪的入射角呈周期性變化； 波流同向要比波流逆向時的錨繩張力要大, 且波流夾角為 135°時, 迎流面錨繩張力最大； 網箱下沉能明顯減小網箱運動幅度和錨繩受力。

各種工況下, 浮環傾角大小在 25°以內, 其值隨流速線性增加, 隨著波高的增加而增大, 但增大的幅度隨著流速和周期的增加而減小。

[1] 張雅芝. 我國海水魚類網箱養殖現狀及其發展前景[J].海洋科學, 1995, 5： 21-24.

[2] 張雅芝, 蘇永全. 論我國海水魚類網箱養殖的可持續發展[J]. 海洋科學, 2001, 7： 52-56.

[3] 徐君義, 金偉良. 淺海抗風浪網箱養魚技術研究[J].海洋科學, 2001, 1： 12-14.

[4] 王福表. 網箱養殖水污染及其治理對策[J]. 海洋科學, 2002, 7： 24-26.

[5] 王福表. 水產養殖清淤網箱的研制和應用[J]. 海洋科學, 2002, 7： 12-14.

[6] 袁軍亭, 周應祺. 深水網箱的分類及性能[J]. 上海水產大學學報, 2006, 03： 3350-3358.

[7] 郭建平, 吳常文. 美國式鋼質升降式大型深水網箱結構原理的研究探討[J]. 漁業現代化, 2004, 1： 28-31.

[8] 章守宇, 劉洪生. 飛碟型網箱的水動力學數值計算法[J].水產學報, 2002, 6： 519-527.

[9] 夏泰淳, 張健. 深水雙錐型網箱的阻力估算[J]. 上海水產大學學報, 2003, 1： 87-91.

[10] 劉健, 夏泰淳, 許柳雄. 深水雙錐型網箱的水動力估算[J].浙江海洋學院學報(自然科學版), 2007, 3： 257-265.

[11] 孫滿昌, 張健, 錢衛國.飛碟型網箱水動力模型試驗與理論計算比較[J].上海水產大學學報, 2003, 4： 319-323.

[12] 李玉成, 宋芳, 董國海, 等. 碟形網箱水動力特性的研究[J].海洋工程, 2004, 4： 19-25.

[13] 李玉成, 桂福坤, 宋芳, 等. 重力式與碟形網箱的錨繩受力特性比較[J].海洋工程, 2005, 4： 19-24.

[14] Fredriksson D W, Muller E, Baldwin K, et al. Open ocean aquaculture engineering： system design and physical modeling[J]. Marine Technology Society Journal, 2000, 34(1)： 41-52.

[15] Tsukrov I I, Ozbay M, Swift M R, et al. Open ocean aquaculture engineering： numerical modeling[J]. Marine Technology Society Journal, 2000, 34(1)： 29-40.

[16] ZHU K Q, CAI Y, YU C L, et al. Nonlinear Hydrodynamic Response of Marine Cable-Body System Undergoing Random Dynamic Excitation[J]. Journal of Hydrodynamics. 2009, 21(6)： 851-855.

[17] 朱克強, 鄭道昌, 張玉松, 等. 隨機波浪下遙控潛水器強非線性耦合空間運動與纜索安全性研究[J]. 海洋工程, 2010, 2： 95-99.

[18] 朱克強, 朱海洋, 于春令, 等. 深海遙控潛水器多體系統非線性耦合動力特性模擬[J]. 海洋工程, 2008, 1： 83-87.

[19] Huang C C, Tang H J, Liu J Y. Effects of waves and currents on gravity-type cages in the open sea[J].Aquacultural Engineering, 2008, 38(2)： 105-116.