基于拉格朗日方程的積油轉(zhuǎn)子系統(tǒng)力學(xué)建模和數(shù)值仿真*

許 濤，王美令，張兆豐，韓清凱

（大連理工大學(xué)機(jī)械工程學(xué)院，遼寧大連 116024）

基于拉格朗日方程的積油轉(zhuǎn)子系統(tǒng)力學(xué)建模和數(shù)值仿真*

許 濤，王美令，張兆豐，韓清凱

（大連理工大學(xué)機(jī)械工程學(xué)院，遼寧大連 116024）

提出一種基于雙支撐轉(zhuǎn)子系統(tǒng)的力學(xué)簡(jiǎn)化模型，分析了含有旋轉(zhuǎn)腔體積油故障的轉(zhuǎn)子系統(tǒng)動(dòng)力學(xué)特性。首先，將轉(zhuǎn)子腔體中積油簡(jiǎn)化為集中質(zhì)量油團(tuán)，采用拉格朗日方程，建立了該系統(tǒng)的動(dòng)力學(xué)方程，基于方程解析，分析了不同轉(zhuǎn)速下系統(tǒng)的位移頻率響應(yīng)變化。結(jié)果表明，積油轉(zhuǎn)子在旋轉(zhuǎn)過(guò)程中，當(dāng)轉(zhuǎn)速超過(guò)系統(tǒng)臨界轉(zhuǎn)速時(shí)，會(huì)出現(xiàn)共振鎖頻現(xiàn)象。

積油轉(zhuǎn)子；拉格朗日方程；數(shù)值仿真

0 引言

旋轉(zhuǎn)機(jī)械作為國(guó)家航空、動(dòng)力、化工、能源領(lǐng)域中重要的機(jī)械裝置，在國(guó)民經(jīng)濟(jì)和國(guó)家安全方面，都占有極其重要的作用，大部分的旋轉(zhuǎn)機(jī)械如汽輪機(jī)、壓縮機(jī)、航空發(fā)動(dòng)機(jī)等裝置內(nèi)部均有腔體盤鼓結(jié)構(gòu)，由于裝置不合理的密封措施或者軸承安裝等裝配上的問(wèn)題，常常導(dǎo)致腔體進(jìn)油或者潤(rùn)滑油泄漏，流入腔體的積油所導(dǎo)致的裝置運(yùn)行故障時(shí)有發(fā)生[1-3]，而由實(shí)驗(yàn)觀察到，即使微量的腔體積油，也會(huì)對(duì)腔體的運(yùn)轉(zhuǎn)產(chǎn)生極大的影響。帶有微量積油的腔體可以稱之為含液轉(zhuǎn)子系統(tǒng)，即在旋轉(zhuǎn)部件空腔內(nèi)積存有微量液體的轉(zhuǎn)子系統(tǒng)，若腔體內(nèi)進(jìn)入一定量的液體，則旋轉(zhuǎn)的液體與轉(zhuǎn)子之間的相互作用會(huì)使得轉(zhuǎn)子在一定的轉(zhuǎn)速范圍內(nèi)出現(xiàn)運(yùn)動(dòng)失穩(wěn)，即積油自身出現(xiàn)嚴(yán)重的自激振動(dòng)[4]。

自從Wolf[5]在1968年首次提出積油轉(zhuǎn)子存在自激不穩(wěn)定區(qū)域后，國(guó)內(nèi)外眾多學(xué)者對(duì)積液轉(zhuǎn)子開(kāi)展了試驗(yàn)和理論方面探索研究工作。Hendricks[6]，Holm[7]，Jorgense[8]分別報(bào)道了懸臂、對(duì)稱支撐、彈性支撐條件下帶有部分充液的剛性轉(zhuǎn)子系統(tǒng)的穩(wěn)定性和渦動(dòng)性，Yoshizumi[9]建立了忽略轉(zhuǎn)子不平衡、重力和陀螺效應(yīng)的彈支充液轉(zhuǎn)子系統(tǒng)的耦合動(dòng)力學(xué)模型。國(guó)內(nèi)復(fù)旦大學(xué)的張文和陶明德[10]基于梁模型和流體二維流動(dòng)模型，推導(dǎo)了充液轉(zhuǎn)子的攝動(dòng)方程，得到了充液轉(zhuǎn)子失穩(wěn)判別的解析表達(dá)式，浙江大學(xué)的祝長(zhǎng)生[11-12]對(duì)部分充液的柔性轉(zhuǎn)子，剛性轉(zhuǎn)子系統(tǒng)振動(dòng)和穩(wěn)定性進(jìn)行了較為全面的研究，從實(shí)驗(yàn)和理論方面分析了充液轉(zhuǎn)子系統(tǒng)不穩(wěn)定產(chǎn)生的過(guò)程，失穩(wěn)過(guò)程中系統(tǒng)的動(dòng)力特性以及流體粘度、充液兩對(duì)轉(zhuǎn)子系統(tǒng)振動(dòng)和穩(wěn)定性的影響。

本文針對(duì)含有旋轉(zhuǎn)腔體積油故障的轉(zhuǎn)子系統(tǒng)，提出一種雙支撐轉(zhuǎn)子系統(tǒng)力學(xué)簡(jiǎn)化模型，將積油簡(jiǎn)化為集中質(zhì)量油團(tuán)，通過(guò)拉格朗日方程，建立系統(tǒng)動(dòng)力學(xué)方程。由數(shù)值仿真，分析了積油轉(zhuǎn)子系統(tǒng)中轉(zhuǎn)速對(duì)積油系統(tǒng)振動(dòng)響應(yīng)的影響，以及積油轉(zhuǎn)子系統(tǒng)的共振鎖頻現(xiàn)象。

1 積油轉(zhuǎn)子系統(tǒng)的力學(xué)建模

1.1 動(dòng)力學(xué)模型建立

將少量漏入的積液轉(zhuǎn)換為集中質(zhì)量油團(tuán)建立的四自由度轉(zhuǎn)子系統(tǒng)力學(xué)模型如圖1所示，剛性軸左右各有兩個(gè)彈性支撐軸承，軸和圓盤一起旋轉(zhuǎn)帶動(dòng)圓盤中簡(jiǎn)化的油團(tuán)一起運(yùn)動(dòng)，圖1中黑色球體表示簡(jiǎn)化的油團(tuán)。不考慮軸的質(zhì)量，設(shè)圓盤質(zhì)量為M，油團(tuán)質(zhì)量為m，轉(zhuǎn)子兩端由軸承B1和B2支撐，并將支撐軸承簡(jiǎn)化為水平豎直剛度形式，如圖1中的K1X，K1Y，K2X，K1Y所示，油團(tuán)旋轉(zhuǎn)過(guò)程中的位移由Cξηz*坐標(biāo)系內(nèi)的軸向位移zB和角位移α共同決定，設(shè)定轉(zhuǎn)子系統(tǒng)轉(zhuǎn)速為Ω。系統(tǒng)基本結(jié)構(gòu)參數(shù)如表1所示。

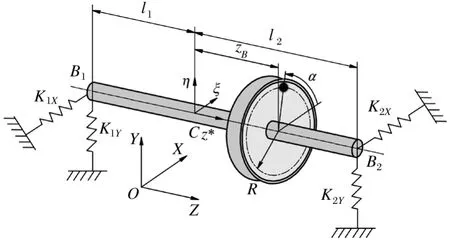
圖1 積油轉(zhuǎn)子系統(tǒng)力學(xué)模型

表1 系統(tǒng)基本結(jié)構(gòu)參數(shù)

在該模型中引入地面固定坐標(biāo)系OXYZ和旋轉(zhuǎn)坐標(biāo)系Cξηz*，其中OXYZ坐標(biāo)系中O為坐標(biāo)原點(diǎn)，Z軸為轉(zhuǎn)子系統(tǒng)的旋轉(zhuǎn)軸線，即左右兩支撐軸承的初始中心線，該坐標(biāo)系固定于地面，坐標(biāo)系Cξηz*為隨轉(zhuǎn)子旋轉(zhuǎn)的旋轉(zhuǎn)坐標(biāo)系，其中C為轉(zhuǎn)子系統(tǒng)的幾何中心。設(shè)定運(yùn)轉(zhuǎn)過(guò)程中不存在軸向位移，當(dāng)系統(tǒng)轉(zhuǎn)速Ω=0時(shí)，默認(rèn)C點(diǎn)和O點(diǎn)重合，則C點(diǎn)在OXYZ坐標(biāo)系的位移向量

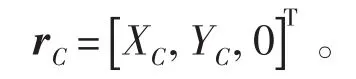
1.2 坐標(biāo)系建立

由于轉(zhuǎn)子系統(tǒng)旋轉(zhuǎn)過(guò)程中復(fù)雜的變形形式，不僅需要考慮到其旋轉(zhuǎn)過(guò)程中的平動(dòng)位移，還應(yīng)考慮整個(gè)裝置在運(yùn)行過(guò)程中的轉(zhuǎn)動(dòng)位移，為了準(zhǔn)確刻畫其運(yùn)動(dòng)形式，引入以下坐標(biāo)系，如圖2所示。

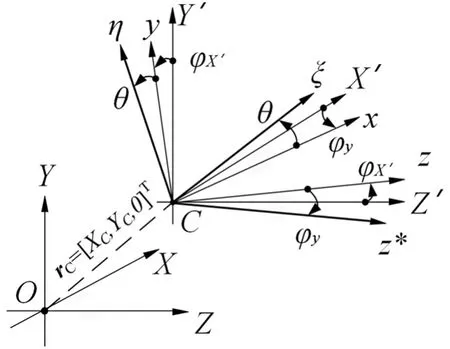
圖2 力學(xué)模型多維坐標(biāo)系

（1）依據(jù)轉(zhuǎn)子幾何中心C點(diǎn)建立坐標(biāo)系CX′Y′Z′，該坐標(biāo)系在系統(tǒng)轉(zhuǎn)速為0時(shí)和坐標(biāo)系OXYZ重合，在旋轉(zhuǎn)過(guò)程中和坐標(biāo)系OXYZ各坐標(biāo)軸平行。

（2）設(shè)定轉(zhuǎn)子系統(tǒng)在CX′Y′Z′坐標(biāo)系內(nèi)沿X′軸角度位移大小為φX′，原坐標(biāo)系沿X′軸旋轉(zhuǎn)角度 φX′得到CX′yz坐標(biāo)系，兩坐標(biāo)系轉(zhuǎn)化向量為R1。

（3）設(shè)定轉(zhuǎn)子系統(tǒng)在CX′yz坐標(biāo)系內(nèi)沿y軸角度位移大小為φy，原坐標(biāo)系沿y軸旋轉(zhuǎn)角度φy得到Cxyz?坐標(biāo)系，兩坐標(biāo)系轉(zhuǎn)化向量為R2。

（4）由于該轉(zhuǎn)子系統(tǒng)為定轉(zhuǎn)速旋轉(zhuǎn)，設(shè)定旋轉(zhuǎn)坐標(biāo)系Cξηz?，該坐標(biāo)系為固定坐標(biāo)系Cxyz?旋轉(zhuǎn)角度θ得到，其中θ=Ωt，其值隨著系統(tǒng)旋轉(zhuǎn)而增大。

已知C點(diǎn)為轉(zhuǎn)子系統(tǒng)的幾何中心，G點(diǎn)為轉(zhuǎn)子系統(tǒng)的質(zhì)心，由于系統(tǒng)會(huì)不可避免存在制造誤差和不平衡受力，幾何中心和質(zhì)心往往不重合，故設(shè)C點(diǎn)和G點(diǎn)在Cξηz?坐標(biāo)系內(nèi)距離偏差為ε，角度偏差為β，同時(shí)，由于偏心的原因，轉(zhuǎn)子的極慣性軸和Cξηz?坐標(biāo)系的η軸也存在一定的角度偏差，設(shè)該角度為 χ，旋轉(zhuǎn)得到Gp1p2p3極慣性矩坐標(biāo)系，如圖3所示。

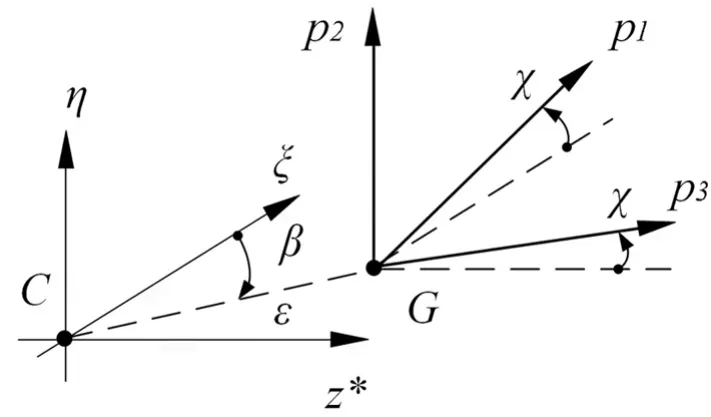
圖3 極慣性矩坐標(biāo)系

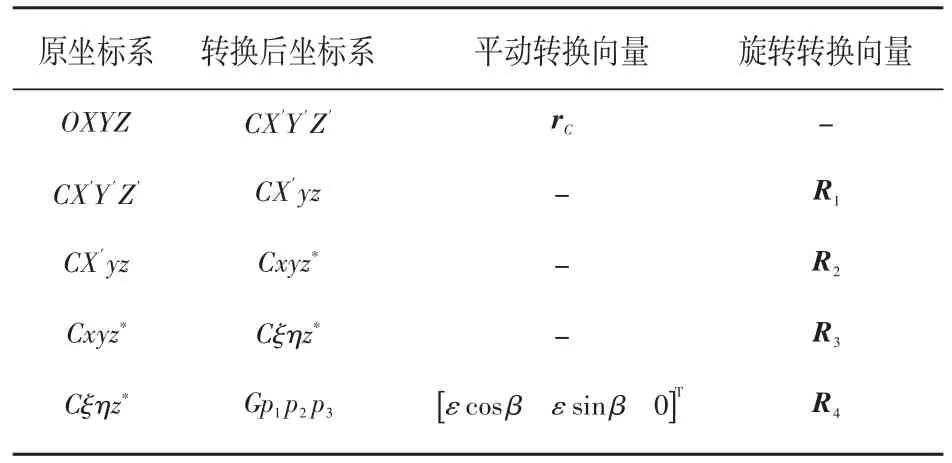
表2 坐標(biāo)系轉(zhuǎn)換及其轉(zhuǎn)換向量

表2中R1，R2，R3，R4轉(zhuǎn)換矩陣表達(dá)式如下

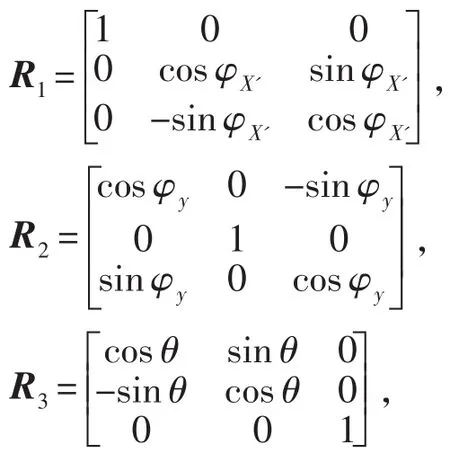
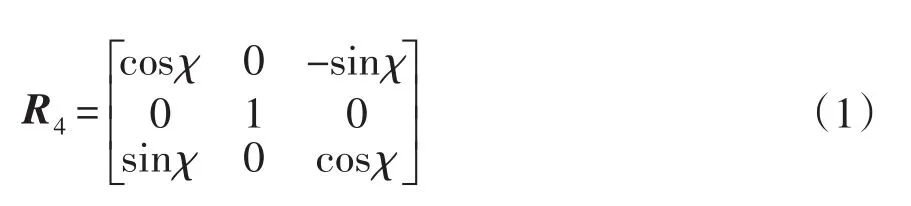
1.3 基于拉格朗日能量求解的動(dòng)力學(xué)方程

本積油轉(zhuǎn)子系統(tǒng)力學(xué)模型中，不考慮廣義力項(xiàng)，則系統(tǒng)的拉格朗日方程為如下形式：

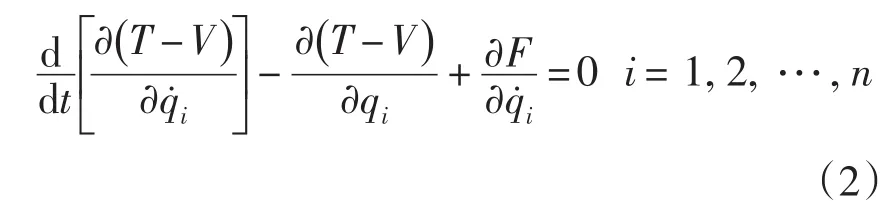
其中，方程廣義坐標(biāo)向量qi為：

系統(tǒng)動(dòng)能為：

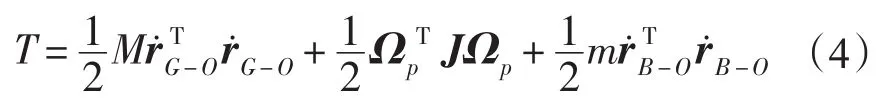
其中，r˙G-O為轉(zhuǎn)子質(zhì)心的速度向量；r˙B-O為油團(tuán)的速度向量；Ωp表示的為轉(zhuǎn)子角速度向量轉(zhuǎn)換到極慣性矩坐標(biāo)系內(nèi)的角速度向量；J表示的為轉(zhuǎn)盤的轉(zhuǎn)動(dòng)慣量矩陣。

系統(tǒng)勢(shì)能求解公式如下[14]：

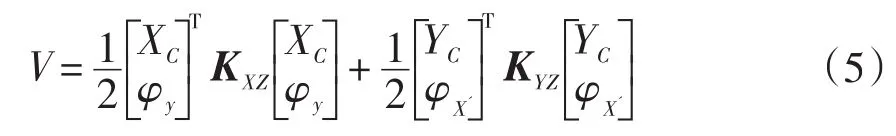
其中，KXZ，KYZ分別表示的是系統(tǒng)在XZ平面的剛度矩陣和在YZ平面的剛度矩陣。

設(shè)油團(tuán)在圓盤軌道內(nèi)的運(yùn)動(dòng)阻尼為cB，考慮瑞利阻尼函數(shù)，則表達(dá)式中阻尼能量為

考慮系統(tǒng)整體阻尼因素的存在，將系統(tǒng)阻尼考慮為瑞利阻尼，即比例阻尼，其求解公式如下

λ和η可由如下公式求得[13]：

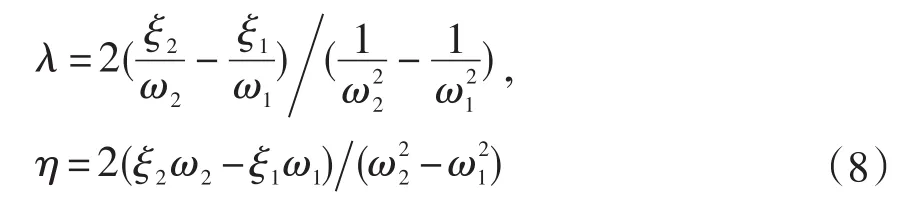
其中，ξ1, ξ2為阻尼系數(shù)，ω1, ω2為轉(zhuǎn)子的一、二階臨界轉(zhuǎn)速。

將方程（4），（5），（6）帶入方程（2）中，并加入系統(tǒng)整體阻尼，得到該積油轉(zhuǎn)子系統(tǒng)的四自由度動(dòng)力學(xué)方程和耦合方程

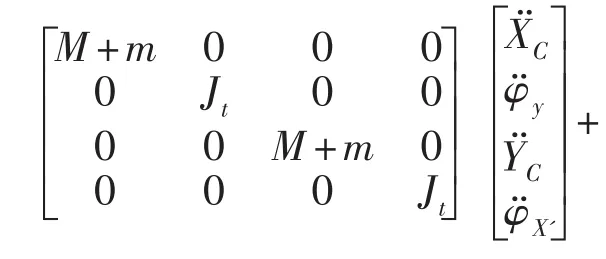
由方程（9）可得系統(tǒng)的質(zhì)量矩陣和剛度矩形式如下

2 積油轉(zhuǎn)子系統(tǒng)的數(shù)值仿真分析

基于系統(tǒng)動(dòng)力學(xué)方程，利用Runge-Kutta數(shù)值法對(duì)該二階多元微分方程進(jìn)行求解，通過(guò)Matlab數(shù)值仿真，采用時(shí)域、頻域、三維譜圖曲線分析了積油轉(zhuǎn)子系統(tǒng)在不同轉(zhuǎn)速下的響應(yīng)形式[15]。

已知積油系統(tǒng)一階固有頻率為33.4 Hz，設(shè)置仿真參數(shù)中積油質(zhì)量為1.85 g，體積為2 ml，仿真測(cè)點(diǎn)為系統(tǒng)的幾何中心C點(diǎn)，設(shè)置仿真分析條件如下：采樣頻率為750 Hz，F(xiàn)FT分析取總采樣數(shù)據(jù)點(diǎn)的后數(shù)據(jù)量，三維譜圖取每組800個(gè)數(shù)據(jù)點(diǎn)作為一組進(jìn)行分析。

（1）轉(zhuǎn)速Ω=10 Hz

仿真測(cè)點(diǎn)振動(dòng)響應(yīng)分析的時(shí)域圖如圖4(a)所示，頻域圖如圖4(b)所示。

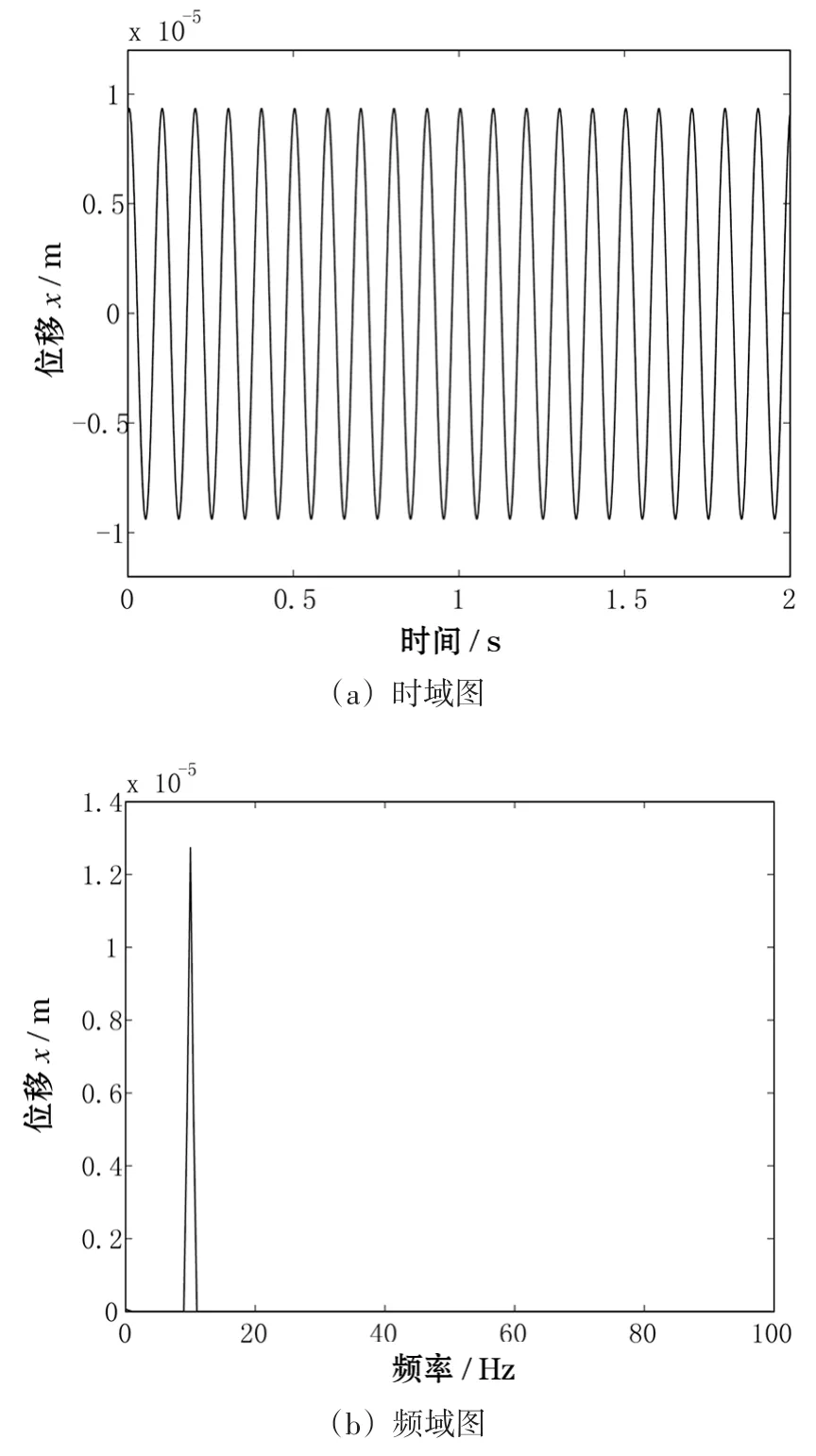
圖4 轉(zhuǎn)速為10 Hz時(shí)系統(tǒng)振動(dòng)響應(yīng)

由圖4可看出，仿真測(cè)點(diǎn)的時(shí)頻曲線達(dá)到穩(wěn)定值，頻譜圖只出現(xiàn)了單一的工頻，沒(méi)有倍頻成分。

（2）轉(zhuǎn)速Ω=20 Hz

仿真測(cè)點(diǎn)振動(dòng)響應(yīng)分析的時(shí)域圖如圖5(a)所示，頻域圖如圖5(b)所示。

由圖5可以看出當(dāng)系統(tǒng)轉(zhuǎn)速上升到20 Hz后，系統(tǒng)的時(shí)域波形出現(xiàn)了波形疊加，整體振幅略高與轉(zhuǎn)速為10 Hz時(shí)的振幅，同時(shí)，系統(tǒng)出現(xiàn)了多階頻率，各頻率成分的幅值變化較大，但頻率成分仍以工頻成分占主導(dǎo)。

（3）轉(zhuǎn)速Ω=40 Hz

仿真測(cè)點(diǎn)振動(dòng)響應(yīng)分析的時(shí)域圖如圖6(a)所示，頻域圖如圖6(b)所示。

圖6中，系統(tǒng)的時(shí)域波形呈周期性變化趨勢(shì)，波形疊加較明顯，最大幅值較圖4、圖5成倍上升，值得注意的特征是，雖然系統(tǒng)轉(zhuǎn)速已經(jīng)越過(guò)臨界轉(zhuǎn)速，但是系統(tǒng)臨界轉(zhuǎn)速時(shí)激起的共振仍然在系統(tǒng)振動(dòng)中占主導(dǎo)成分，同時(shí)，由于此時(shí)轉(zhuǎn)速接近臨界轉(zhuǎn)速，振動(dòng)幅值仍大于10 Hz、20 Hz時(shí)測(cè)點(diǎn)最大振幅。

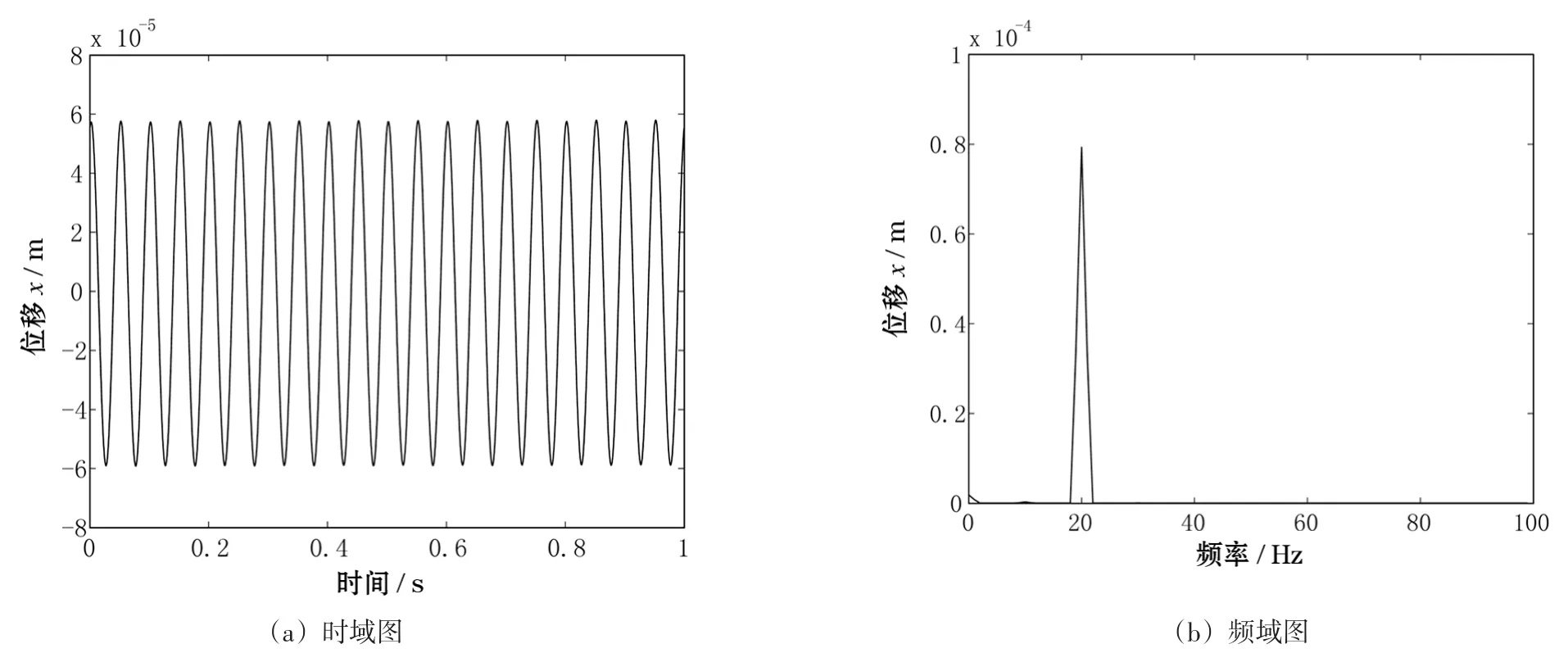
圖5 轉(zhuǎn)速為20 Hz時(shí)系統(tǒng)振動(dòng)響應(yīng)

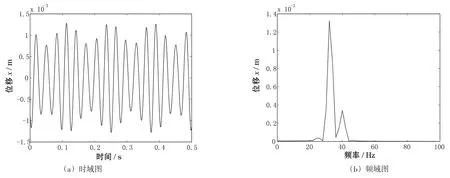
圖6 轉(zhuǎn)速為40 Hz時(shí)系統(tǒng)振動(dòng)響應(yīng)

（4）轉(zhuǎn)速Ω=60 Hz

仿真測(cè)點(diǎn)振動(dòng)響應(yīng)分析的時(shí)域圖如圖7(a)所示，頻域圖如圖7(b)所示。

由圖7可以看出，當(dāng)系統(tǒng)轉(zhuǎn)速上升到60 Hz時(shí)，系統(tǒng)時(shí)域波形仍然為疊加波形，波形平均幅值較40 Hz時(shí)下降較多，但仍高于低轉(zhuǎn)速時(shí)的系統(tǒng)振幅，頻譜圖中仍有多種頻率成分存在，其中臨界轉(zhuǎn)速仍占主導(dǎo)成分，由臨界轉(zhuǎn)速激發(fā)的共振幅值較40 Hz時(shí)也出現(xiàn)下降趨勢(shì)，但高于由系統(tǒng)工頻激發(fā)的振動(dòng)幅值。

（5）位移頻率三維譜圖

考慮以上過(guò)臨界轉(zhuǎn)速后，系統(tǒng)頻譜中始終存在的臨界成分，為了從更大范圍研究此臨界成分，對(duì)該轉(zhuǎn)子系統(tǒng)由5 Hz到75 Hz繪制了位移頻率三維譜圖，如圖8所示。

由圖8積油轉(zhuǎn)子系統(tǒng)x軸方向的三維譜圖可以看出，當(dāng)系統(tǒng)轉(zhuǎn)速低于臨界轉(zhuǎn)速時(shí)，系統(tǒng)以工頻振動(dòng)為主導(dǎo)成分，振動(dòng)幅值較小，到達(dá)臨界轉(zhuǎn)速時(shí)系統(tǒng)振動(dòng)幅值達(dá)到最大，之后系統(tǒng)的工頻振動(dòng)恢復(fù)到較低幅值，但系統(tǒng)的臨界共振并沒(méi)有隨著轉(zhuǎn)速的改變而消失，而是在臨界轉(zhuǎn)速處長(zhǎng)時(shí)間維持在高振幅狀態(tài)，此種振動(dòng)形式即為積油轉(zhuǎn)子系統(tǒng)的共振鎖頻現(xiàn)象。

3 結(jié)論

本文以旋轉(zhuǎn)機(jī)械中常見(jiàn)的積油故障為主要研究對(duì)象，通過(guò)模型簡(jiǎn)化建立了積油轉(zhuǎn)子系統(tǒng)動(dòng)力學(xué)模型，并由數(shù)值仿真，分析研究了轉(zhuǎn)速對(duì)積油轉(zhuǎn)子系統(tǒng)振動(dòng)響應(yīng)的影響。仿真結(jié)果表明，積油轉(zhuǎn)子系統(tǒng)在不同轉(zhuǎn)速下的響應(yīng)變化較為復(fù)雜，在轉(zhuǎn)速低于系統(tǒng)臨界轉(zhuǎn)速時(shí)，系統(tǒng)的振動(dòng)以工頻振動(dòng)為主，當(dāng)轉(zhuǎn)速超過(guò)系統(tǒng)臨界轉(zhuǎn)速后，系統(tǒng)表現(xiàn)出獨(dú)特的共振鎖頻現(xiàn)象，最大振幅始終維持在臨界轉(zhuǎn)速處，并伴有一定幅值的工頻振動(dòng)。本結(jié)論驗(yàn)證了文獻(xiàn)[4]中的實(shí)驗(yàn)和分析結(jié)果，并為轉(zhuǎn)子系統(tǒng)積油故障的辨識(shí)和處理提供了一定的理論支撐。

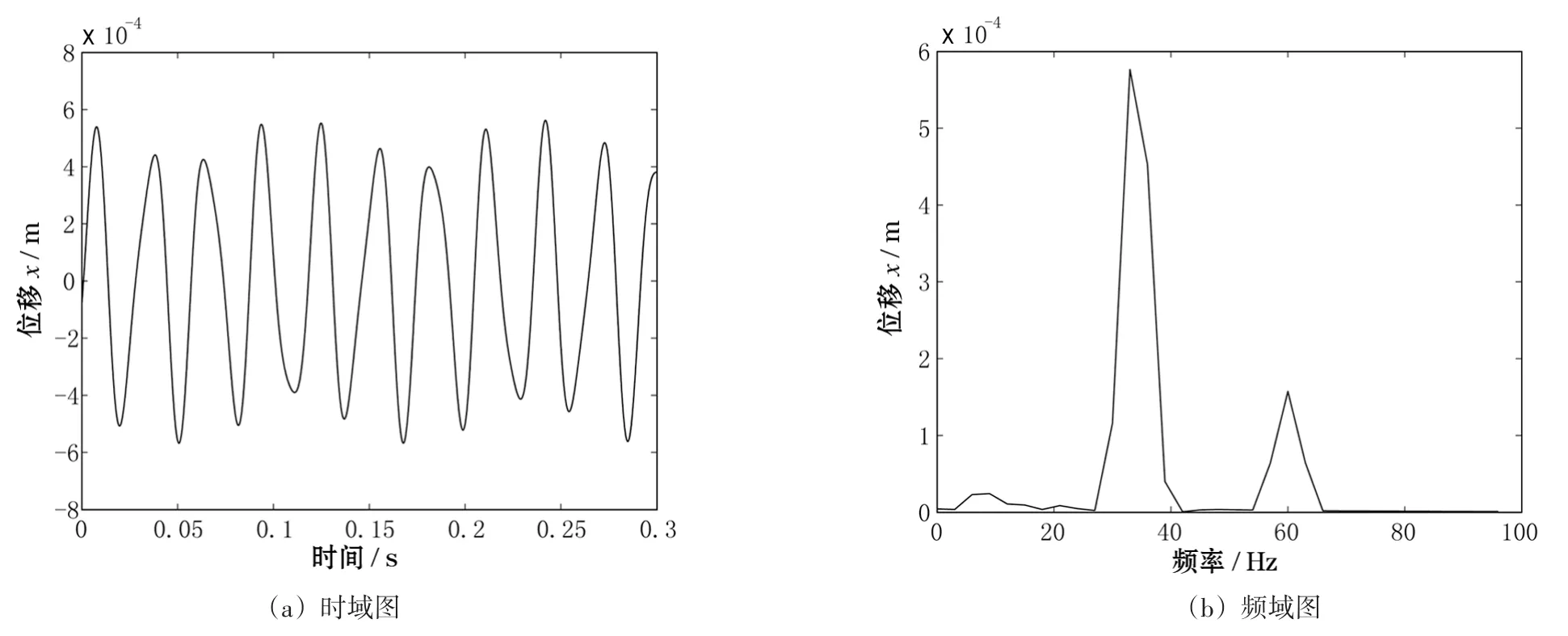
圖7 轉(zhuǎn)速為60 Hz時(shí)系統(tǒng)振動(dòng)響應(yīng)

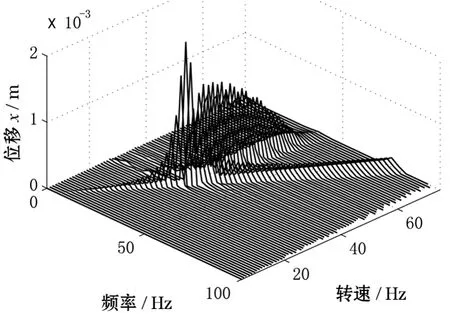
圖8 積油轉(zhuǎn)子系統(tǒng)x軸方向三維譜圖

［1］羅劍斌，盧一兵，袁立平，等.汽輪機(jī)轉(zhuǎn)子中心孔進(jìn)油引起的振動(dòng)分析［J］.電力安全技術(shù)，2005（7）：6-7.

［2］張其顯，劉曉鋒.汽輪機(jī)轉(zhuǎn)子中心孔進(jìn)油誘發(fā)異常振動(dòng)故障分析診斷［J］.汽輪機(jī)技術(shù)，2007，49（1）：57-59.

［3］姜廣義，武鵬，張潔.航空發(fā)動(dòng)機(jī)腔內(nèi)積油引發(fā)振動(dòng)故障分析［J］.航空發(fā)動(dòng)機(jī)，2013，39（2）：75-78.

［4］Q.Han，M.Wang，H.Chu.Nonsynchronous Vibrations of Rotor System with an Oil-Block inside the Rotating Drum［J］.Advances in Vibration Engineering，2013，12（2）：165-178.

［5］Wolf J A.Whirl Dynamics of a Rotor Partially Filled With Liquid［J］.Journal of Applied Mechanics，1968，35（4）：676-682.

［6］Hendricks S L.Stability of a Clamped-Free Rotor Partial?ly Filled With Liquid［J］.Journal of Applied Mechan?ics，1986，53（1）：166-172.

［7］Holm christensen O，Trager K.A Note on Rotor Instabili?ty Caused By Liquid Motions［J］.Journal of Applied Mechanics，1991，58（3）：804-811.

［8］Coldingjorgensen J.Rotor Whirl Measurements on a Long Rotating Cylinder Partially Filled With Liquid［J］.Jour?nal of Vibration and Acoustics， 1993， 115（2）：141-144.

［9］Yoshizumi F.Self-Excited Vibration Analysis of a Rotat?ing Cylinder Partially Filled with Liquid［J］.Journal of System Design and Dynamics，2011，5（2）：372-387.

［10］Tao M，Zhang W.Dynamic stability of a flexible spin?ning cylinder partially filled with liquid［J］.Journal of Applied Mechanics，2002，69（5）：708-710.

［11］祝長(zhǎng)生.部分充液懸臂柔性轉(zhuǎn)子系統(tǒng)不穩(wěn)定特性的實(shí)驗(yàn)研究［J］.振動(dòng)工程學(xué)報(bào)，2004，（04）：65-68.

［12］Zhu C S.Experimental Investigation Into the Effect of Fluid Viscosity on Instability of an Over-hung Flexible Rotor Partially Filled With Fluid［J］.Journal of Vibra?tion and Acoustics，2006，128（3）：392.

［13］韓清凱，于濤，王德友.故障轉(zhuǎn)子系統(tǒng)的非線性振動(dòng)分析與診斷方法［M］.北京：科學(xué)出版社，2010.

［14］ Genta G.Dynamics of rotating systems［M］.New York：Springer，2005.

［15］毛丁輝，邱建琪，史涔溦.基于SVPWM的電動(dòng)汽車直接轉(zhuǎn)矩控制方法研究［J］.機(jī)電工程，2014（07）：830-835.

Mechanical Modeling and Numerical Simulation of Oil Leakage Rotor System Based on the Lagrange Equation

XU Tao，WANG Mei-ling，ZHANG Zhao-feng，HAN Qing-kai
（School of Mechanical Engineering，Dalian University of Technology，Dalian 116024，China）

On account of the operation faults caused by the oil leakage in rotor cavity，to explore its dynamic characteristics，a double-support simplified rotor model has been proposed.In the model，leak oil is transformed into a concentrated mass oil-block.Then the dynamic equation is deduced by the Lagrange equation，based on the numerical simulation，vibration responses caused by the rotating speed are investigated.Result shows that frequency-locking phenomenon will appear when the rotating speed exceeds the first critical speed.

oil leakage rotor；Lagrange equation；numerical simulation

TH123

A

1009－9492(2015)10－0055－06

10.3969/j.issn.1009-9492.2015.10.014

許 濤，男，1989年生，河南信陽(yáng)人，碩士研究生。研究領(lǐng)域：轉(zhuǎn)子動(dòng)力學(xué)，故障診斷。

(編輯：向 飛)

*國(guó)家重點(diǎn)基礎(chǔ)研究發(fā)展計(jì)劃（973計(jì)劃）資助項(xiàng)目（編號(hào)：2012CB026000）；國(guó)家自然科學(xué)基金資助項(xiàng)目（編號(hào)：51175070）

2015－05－28