用剛性表面球形傳聲器陣列重構入射波聲場與識別定位聲源*

李敏宗，盧奐采，2*，金江明

（1.浙江工業大學機械工程學院，特種裝備制造與先進加工技術教育部/浙江省重點實驗室，杭州310014；2.浙江工業大學，浙江省信號處理重點實驗室，杭州310014）

用剛性表面球形傳聲器陣列重構入射波聲場與識別定位聲源*

李敏宗1，盧奐采1，2*，金江明1

（1.浙江工業大學機械工程學院，特種裝備制造與先進加工技術教育部/浙江省重點實驗室，杭州310014；2.浙江工業大學，浙江省信號處理重點實驗室，杭州310014）

剛性表面球形傳聲器陣列是測量三維聲場常用的前端，由于剛性球面對入射波聲場有散射影響，直接測量值不是原入射波聲場的聲壓值，因而不能使用在自由聲場條件下建立的聲場模型和近場聲全息方法來重構入射波聲場。通過剛性球體表面聲波散射的數學模型，建立起入射波聲壓與發生散射后總聲壓之間的關系，進而通過剛性表面球形傳聲器陣列測量聲壓，計算入射波聲場分布，并進行聲源識別定位。通過仿真與實驗，檢驗了球面入射波遇到剛性表面球體發生散射后，球體表面處聲壓分布的變化。由球面近場聲全息方法，重構球形陣列表面及外部空間的入射波聲場，檢驗了波數、重構距離參數變化對聲場重構精度的影響。結果表明：采用剛性表面球形傳聲器陣列測得的聲場總聲壓，運用根據聲波散射模型建立的球面近場聲全息方法，可以以一定的精度重構出入射波聲場的三維空間分布。

球形傳聲器陣列；入射波聲場重構；球面近場聲全息；聲波散射；剛性表面球體

球形傳聲器陣列，由于其球面所具有的經緯角全指向性和三維對稱性，能夠測量聲壓場的三維空間分布，因而對于封閉空間（如飛機、汽車和房間內部）的聲場重構、聲源識別定位等應用，具有獨特優勢［1-5］。球形傳聲器陣列是指在一個固定半徑的球面上按照一定的幾何規律和優化準則［6］，布置一組傳聲器而形成的聲場全息聲壓測量陣列。按照結構可以分為空心球形陣列與剛性表面球形陣列，空心球形陣列指的是將各個傳聲器固定在指定的位置，傳聲器的表面形成一個虛擬球面的若干個節點，它的聲場理論模型假設聲場不受陣列影響，然而在應用時由于聲場中引入了傳聲器支架與導線等因素，實際上（尤其在聲音頻率較高時）滿足不了此假設條件［3］。剛性表面球形陣列是指將傳聲器鑲嵌到具有剛性表面的球面殼體上，由于剛性表面對入射聲波產生的散射，球形陣列上傳聲器測量的聲壓值，不是原入射波聲場的聲壓值，因此不能直接將其應用于自由聲場條件下建立的聲場模型和近場聲全息方法，來重構入射波聲場，而需要考慮球形傳聲器陣列的剛性表面在聲場中發生的散射現象，建立考慮散射現象的聲場的數學模型。所幸的是，剛性表面球體對入射波聲場的散射在聲學領域是一個經典問題，其理論分析與數值計算結果在理論聲學相關專著中［7-9］均具有闡述，本文以入射波在剛性球形表面產生散射的數學模型為基礎，推導對應的球面近場聲全息算法，最終由剛性表面球形陣列上傳聲器所測得的聲場總聲壓數據，重構出陣列周圍空間的入射波聲壓的三維空間分布，進而進行聲源識別定位。

目前，剛性表面球形傳聲器陣列多用于遠場測試，結合波束形成方法［10-12］進行三維空間的聲源識別定位。由于剛性表面球形傳聲器陣列在近場可結合近場聲全息方法進行聲場重構，在球狀或類似于球狀的內部封閉空間中的聲源識別定位有獨特優勢，故在該方向的研究也有一定進展。2008年，Finn Jacob?sen［2］在球面近場聲全息方法中，考慮了剛性表面球形傳聲器陣列的聲波散射影響，在仿真中給出了陣列中心與聲源連線上的重構聲壓分布，將其與基準聲壓進行了對比，并在實驗中比較了空間中單個點位置處的重構聲壓與測量聲壓的幅值，但沒有進行三維空間的聲場重構誤差的分析與聲源識別定位的驗證；2010年，Earl G.Williams［3］使用剛性表面球形傳聲器陣列，進行了聲場重構的研究，在不同半徑的重構球面上，進行了三維空間的聲場重構誤差分析，并在點聲源的聲場環境下，進行了聲場重構與聲源識別定位的驗證，其論文也通過考慮剛性球面的散射模型，得出了修正的傳播因子，但根據此修正傳播因子計算出的聲場為陣列表面及外部空間聲場的總聲壓分布，而不是僅僅由入射波形成的聲場的聲壓分布。本文的研究內容為：在球面近場聲全息方法中應用剛性球面的聲波散射模型，計算出重構的入射波聲壓在整個三維空間的分布，并在不同波數下，進行不同半徑的重構球面上聲場重構誤差分析；通過重構出的三維空間入射波聲壓分布，進行三維空間的聲源識別定位，并使用剛性表面球形傳聲器陣列進行實驗驗證。

本文首先在第1節中根據剛性球面發生聲波散射的Neumann邊界條件，建立聲波散射數學模型，進而得出剛性球面散射前入射波聲壓與散射后總聲壓之間的數學關系。通過仿真，檢驗球面入射波遇到剛性表面球形傳聲器陣列時發生散射后的聲場變化規律。然后在第2節中，將檢驗由球形傳聲器陣列測量的散射后總聲壓，通過球面近場聲全息方法，重構入射波形成的聲場，以及參數對重構精度的影響。最后在第3節中給出結論。

1 剛性球體表面聲波散射的數學模型

1.1 剛性表面球體引起聲波散射的數學模型

在各向同性聲傳播介質中，入射聲波可由Helmholtz方程的解的形式表示為：

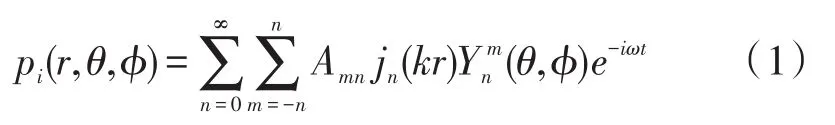
式中：（r，θ,?）為聲場中任意一點的球坐標，pi為此點處入射波的聲壓，ω表示角頻率，k為波數（k=ω/c，c為聲音在空氣介質中的傳播速度），t表示時間。jn(kr)為球貝塞爾函數，表示聲場徑向即r方向的解；為球諧函數，表示聲場θ和?方向的解；Amn為波動方程特解的系數。對于穩態聲場，可將時間依賴性因子e-iωt略去。

假設在聲場空間中放置一個半徑為a的剛性表面球體，其球心與坐標系原點重合，則剛性球體表面會引起入射波的散射現象，并且球面所發出散射聲波的頻率與入射波的頻率相同。聲場總聲壓 pt由入射波的聲壓pi與散射波的聲壓ps疊加而成：

剛性球體表面向外輻射的散射聲波可表示為：

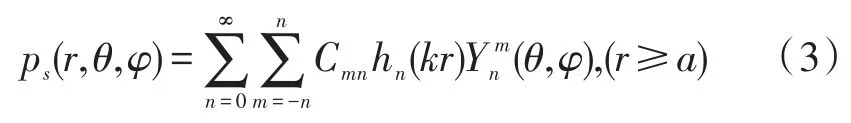
其中hn(kr)為第一類球漢克爾函數，Cmn為球諧函數的系數。

由于剛性球體表面不會吸收入射波的能量，故將其完全散射出去。同時，剛性球面也不會由于散射而變形，因此，球面處的法向介質粒子速度即總聲壓的梯度為零，剛性球面發生散射的Neumann邊界條件［7-9］可由下式表示：

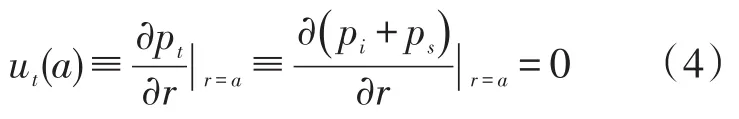
其中，ut(a)表示剛性球面上的法向介質粒子速度，將其結合于公式（1）與公式（3）可得出：

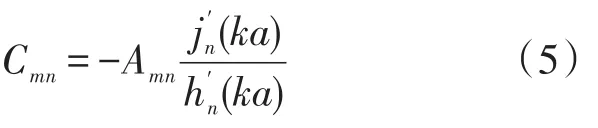
式中：‘′’為求導符號。從而散射波的聲壓ps，可以表示為：

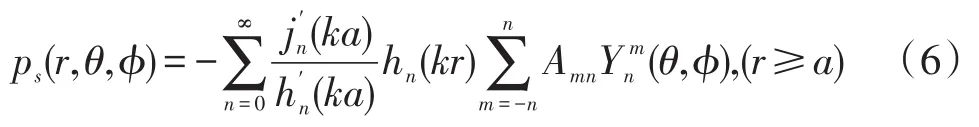
于是，根據公式（1）可得到聲場總聲壓（pt）為：

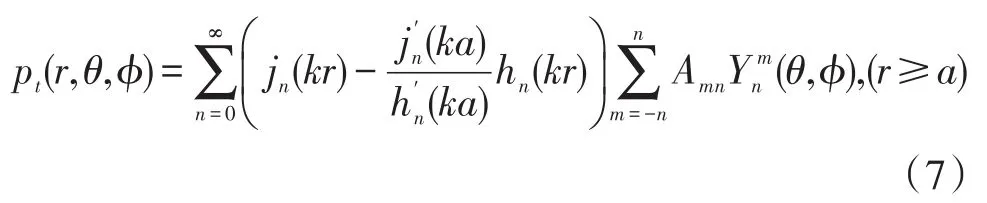
在這里，根據剛性球面的Neumann邊界條件得出散射波與入射波的關系，從而進一步得出經過剛性表面球體散射之后的總聲場模型。對于鑲嵌在剛性表面球形陣列上的傳聲器，在應用中測得的是散射后的聲場總聲壓，根據式（1）與式（7）即可計算出發生散射前的入射波聲場聲壓。

1.2 剛性表面球體引起聲波散射后聲場的變化

對于剛性表面球形傳聲器陣列，各傳聲器都鑲嵌在球體的剛性表面上，測量與記錄聲場的聲壓。因此，研究球形傳聲器陣列表面處發生的散射現象，對于運用球形傳聲器陣列測量聲壓，進行近場聲全息或其它用途的聲學計算分析具有重要意義。本小節對球面入射波聲場進行分析，先給出球面波聲場聲壓的球諧函數展開形式的解析公式，然后檢驗球面入射波在遇到剛性表面球形傳聲器陣列時，散射發生前后球體表面處聲壓分布的變化。

假設球面波由（rs，θs，?s）處單極子點聲源發出，則空間中任意一點（r，θ，?）處的聲壓可以表示為［13］：

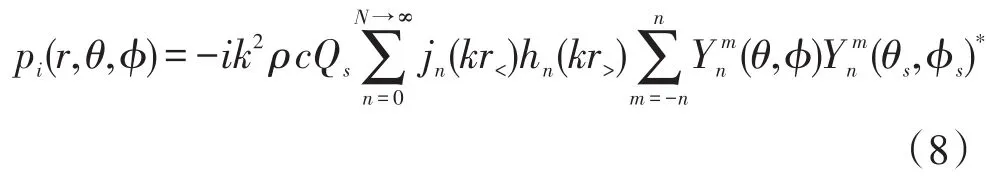
其中符號‘*’表示復數共軛，ρ為介質的密度，Qs為球面波聲源強度，N為球諧函數的截止項數，在本文中取N=30。式中r＜表示r與rs兩者中取值較小者，r＞表示r與rs兩者中取值較大者。

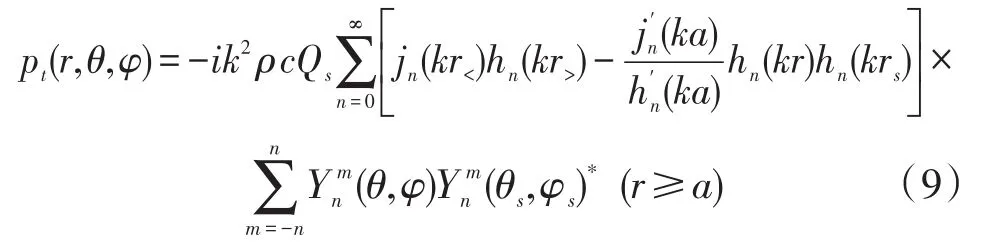
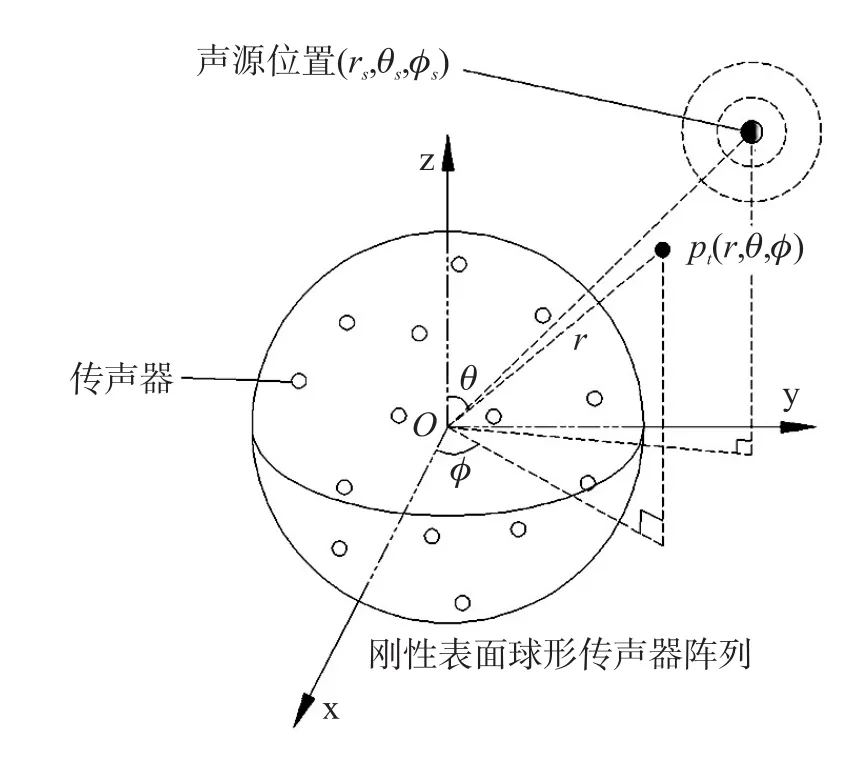
圖1 剛性表面球形傳聲器陣列與球面入射波示意圖

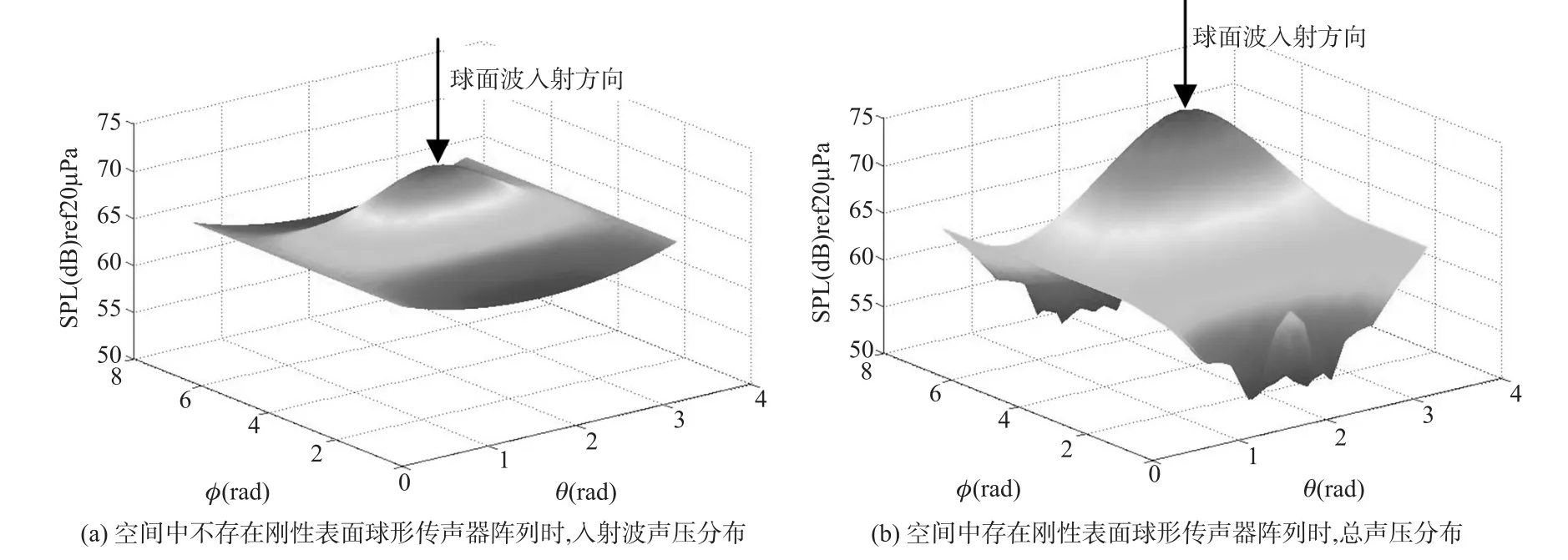
圖2 球面入射波聲場中球形傳聲器陣列剛性表面（r=a）處聲壓分布圖。入射波為來自位于點（r0，θ，φ）=（0.4 m，π/2，π）發出的球面波。（ka=5，a=0.2 m）

設置陣列半徑a為0.2 m，球面波聲場由一個位于（rs，θs，?s）=（0.4 m，π/2，π）處的單極子聲源生成，無量綱頻率（dimensionless frequency）ka為5。在上述參數下，得出球面的聲壓分布如圖2所示。在空間中不存在障礙物時，虛擬球面（r=a）的聲壓分布如圖2（a）），聲壓值在正對聲源處最大，在背對聲源處最小，球面上聲壓值的變化較為平緩；而當剛性表面球形傳聲器陣列存在時，球面聲壓分布如圖2（b）），在正對聲源的球面區域，總聲壓增大且有最大峰值，其它處的聲壓值則迅速減小，并且在背對聲源處的聲壓分布有一個突起。

2 入射波聲場的重構

本節將剛性球體表面散射模型應用于球面近場聲全息方法中，通過仿真和實驗檢驗由剛性表面球形陣列上傳聲器測量的散射后總聲壓，重構由入射波單獨形成的聲場，以及參數對重構精度影響。

2.1 球面近場聲全息方法

球面近場聲全息方法［1-5］，由布置于球形陣列上傳聲器所測得的聲壓，通過聲場逆向空間變換，重構出處于近場空間或聲源結構表面的聲學量分布。聲場重構公式如下：

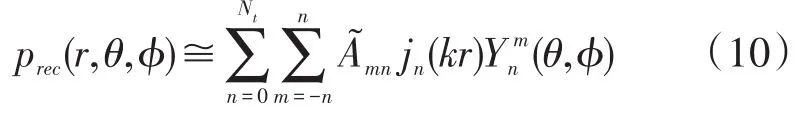
式中：prec(r,θ,?)為位置(r,θ,?)處的重構聲壓，Nt為基函數截止項數，取值與傳聲器數目相關，A~mn為未知系數。

對于剛性表面球形傳聲器陣列，基于考慮剛性球面對入射波的散射影響的聲場模型，可重構出散射前的入射波聲場。根據第1.1節中入射波聲場與總聲場的關系，即公式（7），可得出系數A~mn為：

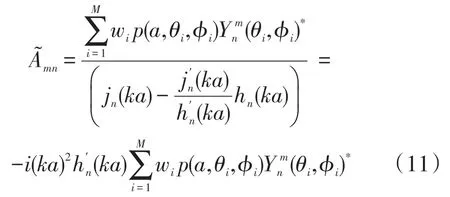
式中：p(a,θi,?i)為第i個傳聲器坐標處的聲壓值；wi為該點相應的權重，由球面數值積分方法確定；M為傳聲器的數目。

2.2 入射波聲場重構的仿真

上節中介紹了使用剛性表面球形傳聲器陣列測量的聲場總聲壓，重構入射波聲場的球面近場聲全息方法和數學模型，本節將檢驗各參數對聲場重構精度的影響。

設置聲場環境由一個位于（r0，θ，?）=（0.5 m，π/2，π）處的單極子聲源生成；剛性表面球形傳聲器陣列位于坐標系原點，陣列半徑a=0.2 m，傳聲器數目為M=64。球形陣列上各傳聲器在根據公式（9）測得總聲壓數據，引入信噪比為40 dB的隨機測量噪聲，再使用這些帶有隨機測量噪聲的總聲壓數據，運用球面近場聲全息理論，進行聲場重構計算。由式（10）與式（11），可重構出空間中任意一點處的入射波聲壓prec(r,θ,?)，再將其與相同位置的聲壓理論值pthe(r,θ,?)（由公式（8）得出）進行比較。在本文中將重構一個以球形陣列中心為球心的球面（a≤R≤rs，其中R為重構球面的半徑）上的聲壓分布，在此球面上均勻的取出Q點，聲壓在這些點的歸一化最小二乘（normalized least-squares）重構誤差［14］定義為ε：

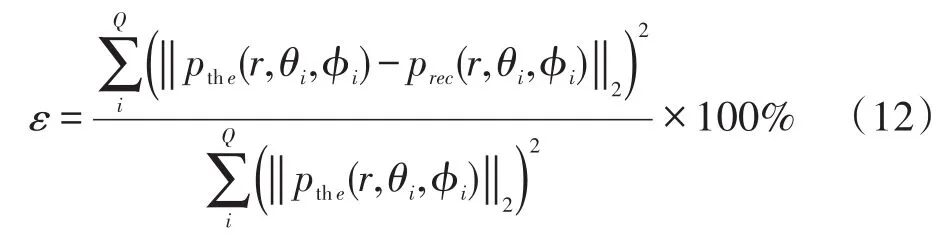
式中：‖?‖2表示二范數。

圖3為在波數k=15下，球形陣列表面上重構的入射波聲壓分布，其與入射波聲壓理論值的誤差為ε=0.28%。可見，采用考慮了球面散射模型的球面近場聲全息方法，在陣列表面處重構的聲場聲壓分布，可以達到非常高的重構精度。

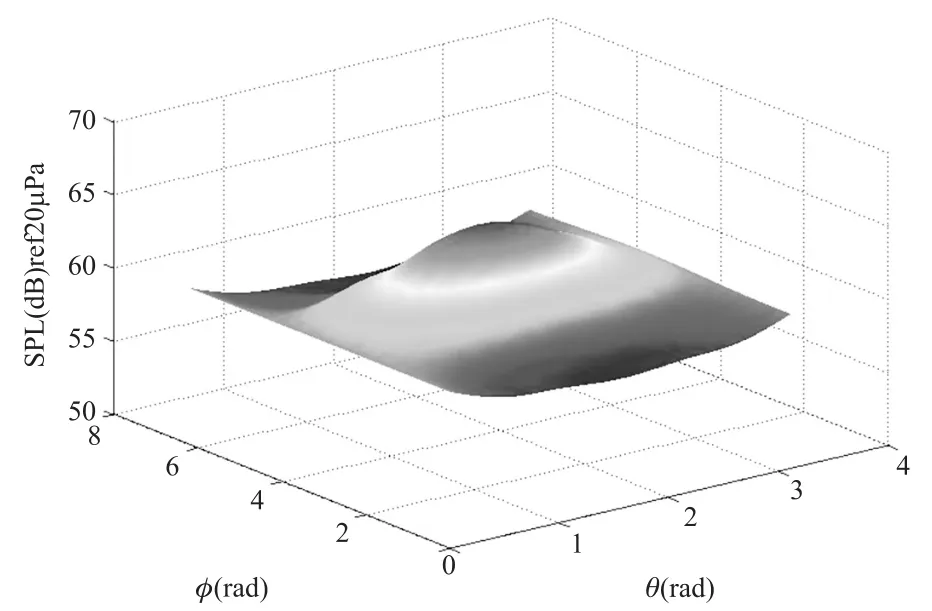
圖3 球面近場聲全息方法重構出的球形陣列表面入射波聲壓分布（a=0.2 m，k=15，M=64，R=0.2 m SNR=40 dB）

由圖3的結果得出，球面近場聲全息方法可重構出球形陣列表面處聲壓分布。而在實際應用中，需要重構球形陣列外部空間的入射波聲壓分布，以作為聲源識別定位的依據。圖4為波數分別為k=5、k=15、k= 25時，重構誤差ε隨著重構半徑R增大的變化。

圖4 在不同波數下聲壓重構誤差隨重構球面半徑的變化（a=0.2 m，M=64，SNR=40 dB）

由圖4可見，在考慮了剛性球體表面聲波散射的入射波聲場重構計算中，當聲壓測量信號的信噪比為SNR=40 dB和球形陣列的傳聲器數目M＝64時，重構半徑R由0.2 m增大至0.25 m的范圍內，在波數k分別為5、15、25的情形下，重構誤差ε均在10%以下，這說明在球形陣列外部較近的區域，聲場重構能取得較高的精度。這是因為球形陣列測得了足夠多的由重構球面傳播來的聲場近場信息。隨著重構半徑R的增大，即重構球面與聲源之間距離的減小，重構誤差ε也隨之增大，特別是當波數k較大時，重構誤差ε隨重構半徑R增大而急劇增大，比如在波數k為25的情形下，重構半徑R由0.2 m增大至0.5 m時，重構誤差由2.3%增大至90%，這是因為重構半徑R越大，球形陣列采集到由重構球面傳播來的近場信息即高波數信息越少，因而重構誤差ε越大。而當波數k較小時，重構誤差ε則隨重構半徑R增大較緩慢地增大。如圖4所示，當重構半徑R由0.2 m增大至0.5 m范圍內，在波數k為15時，重構誤差由0.4%增大至69.2%，而在波數k為5時，重構誤差僅由0.1%增大至23.7%，這是因為當波數較小時，即使重構半徑R較大，球形陣列依然采集到了足夠的由重構球面傳播來的近場信息，因而重構誤差ε相對較小。

圖5為波數k=15，重構半徑R=0.5m，即聲源所在重構球面處的入射波聲壓分布圖，圖5（a））為由球面近場聲全息方法重構的入射波聲壓分布，圖5（b））為根據公式（12）得出的入射波聲壓理論值的分布。此情形下，由于波數k及重構半徑R較大，因而重構誤差ε較大，為69.2%。但是，依然可以通過重構的入射波聲壓分布圖，明顯識別出聲源的方位為（π/2，π）。

上述研究結果表明，使用球面近場聲全息方法進行入射波聲場的重構，在剛性表面球形陣列較近的區域，有較高的重構精度，在球形陣列表面上的重構精度最高。當聲源輻射含有較高的波數k的情形下，在球形陣列測量總聲壓的信噪比SNR和陣列傳聲器數目M不變時，可將球形陣列盡量置于聲源的附近，即縮短重構半徑R，聲源近場的入射波聲場重構的誤差ε，將會明顯減小。

2.3 入射波聲場重構的實驗驗證

在實驗中，使用剛性表面球形傳聲器陣列測量總聲壓，運用球面近場聲全息方法，重構球形陣列表面及外部空間區域的入射波聲場。實驗布置如圖6所示，剛性表面球形傳聲器陣列上，各傳聲器處的聲壓，通過B&K-LANXI設備采集，并通過PULSE軟件進行FFT處理得到聲壓頻域數據，進而可進一步進行聲場重構的計算。實驗在全消聲室內進行，球形陣列的球心設為坐標系中心；在球形陣列外部空間，布置一個揚聲器作為聲源，揚聲器與功放設備控制模塊相連接，發出指定頻率的聲音。

圖6 實驗布置照片

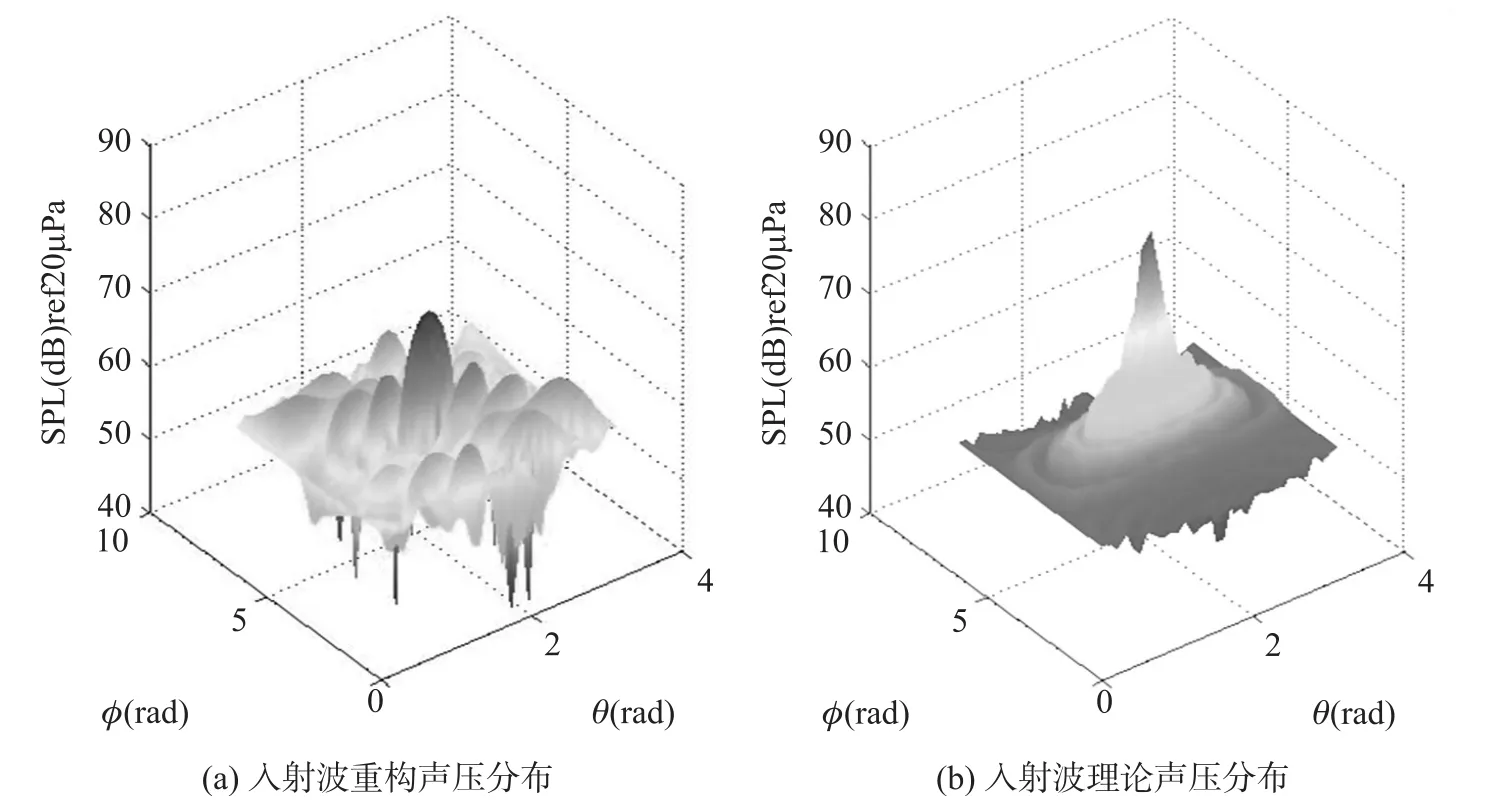
圖5 聲源所在球面處聲場聲壓重構值與理論值比較（a=0.2 m，k=15，M=64，R=0.5 m，SNR=40 dB）

2.3.1 實驗I

在本實驗中，使用一個剛性表面球形傳聲器陣列作為測量前端，球形陣列的半徑a為0.15 m，陣列上傳聲器的數目M為64。按照上述實驗設置，將揚聲器放置在距離陣列中心0.2 m處，聲源頻率f為800 Hz，即波數k為14.8，使用球形陣列測量聲場總聲壓，然后重構球形陣列表面入射波聲壓分布，如圖7所示。

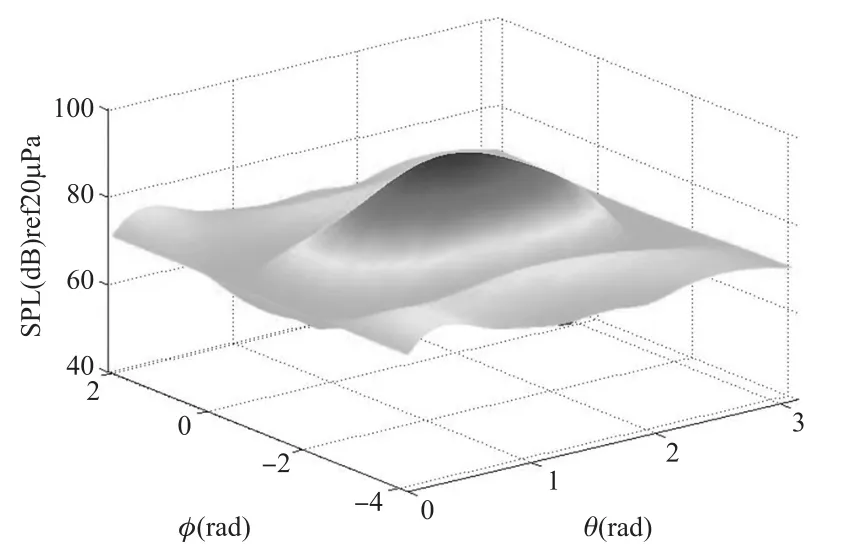
圖7 波數k為14.8時，由球面近場聲全息方法重構出的球形陣列表面處入射波聲壓分布（陣列半徑a=0.15 m，聲源離陣列中心距離d=0.2 m，傳聲器數目M=64）

將各傳聲器位置處重構聲壓與各傳聲器所測得聲壓進行比較，結果如圖8所示，由公式（12）可得它們之間的偏差達20.2%，說明聲場分布在經過剛性球面散射后變化很大，因而分析由剛性球面引起的聲波散射現象，對由剛性表面球形傳聲器陣列重構入射波聲場的研究有著重要意義。

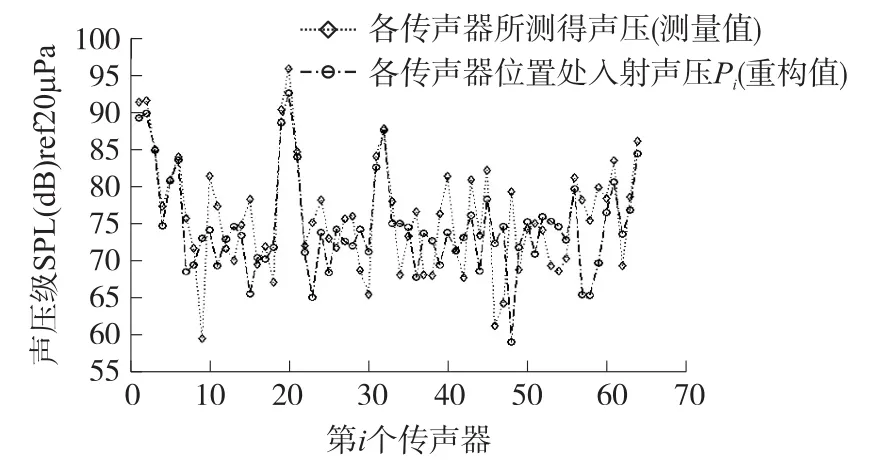
圖8 各傳聲器位置處聲壓的測量值與入射波聲壓重構值比較（陣列半徑a=0.15 m，聲源離陣列中心距離d=0.2 m，傳聲器數目M=64，波數k=14.8）

將重構面半徑設定為R=0.2 m，根據傳聲器測量的總聲壓，運用球面近場聲全息方法，可得出聲源所在球面處的入射波聲壓分布，如圖9所示，通過此聲壓分布圖可以明顯得出，聲源的方位為（1.5 rad，-1.1 rad）。

2.3.2 實驗II

在本實驗中，使用一個B&K公司的剛性表面球形傳聲器陣列［15］作為測量前端，陣列的半徑a為0.097 5 m，陣列上傳聲器的數目M為36。按照實驗I的布置，作為聲源的揚聲器放置于（0.13 m，1.6 rad，4.7 rad）處。在剛性表面球形陣列外部空間中，放置一個1/4英寸檢驗傳聲器，位于（0.107 5 m，1.6 rad，5.2 rad）處，其方位對應于球形陣列表面處編號為7的傳聲器，兩者相距1 cm，用于檢驗入射波聲場重構的精度。

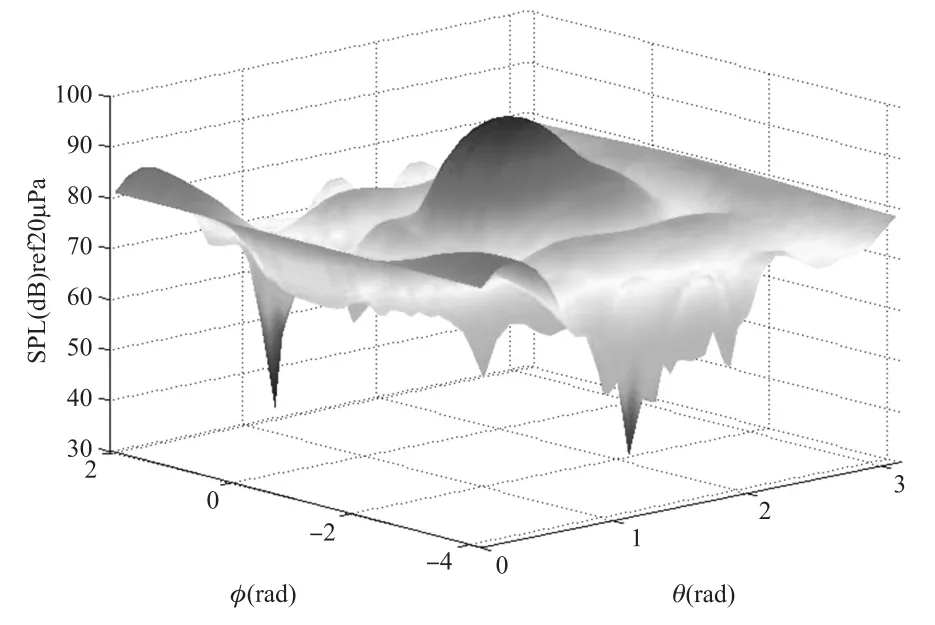
圖9 球面近場聲全息方法重構出的聲源所在球面處入射波聲壓分布（陣列半徑a=0.15 m，聲源離陣列中心距離d=0.2 m，傳聲器數目M=64，波數k=14.8）

實驗步驟如下：首先分別設置聲源頻率f為200 Hz、500 Hz、800 Hz、1 500 Hz、2 500 Hz、4 000 Hz，由球形陣列與聲場中傳聲器進行聲壓信號測量。然后，將球形陣列移開，則聲場中只有聲源與檢驗傳聲器，保持它們的位置不變，再次分別在聲源頻率f為200 Hz、500 Hz、800 Hz、1 500 Hz、2 500 Hz、4 000 Hz的情形下，由此檢驗傳聲器測量入射波聲場的聲壓信號。由實驗步驟可知，前一次球形陣列與檢驗傳聲器，測量的信號為總聲壓值，而后一次檢驗傳聲器的測量值為入射波聲場的聲壓值。根據第2節介紹的入射聲場重構理論，可采用前一次球形陣列測量到的總聲壓值，重構出檢驗傳聲器位置的入射波聲場聲壓值，并與檢驗傳聲器直接測量的入射波聲場聲壓減小對比，以檢驗其聲場重構的計算精度。在上述各實驗頻率下，在檢驗傳聲器位置處，直接測量總聲壓值、直接測量入射波聲場聲壓值以及運用近場聲全息方法重構得出的入射波聲場聲壓值，如圖10所示。

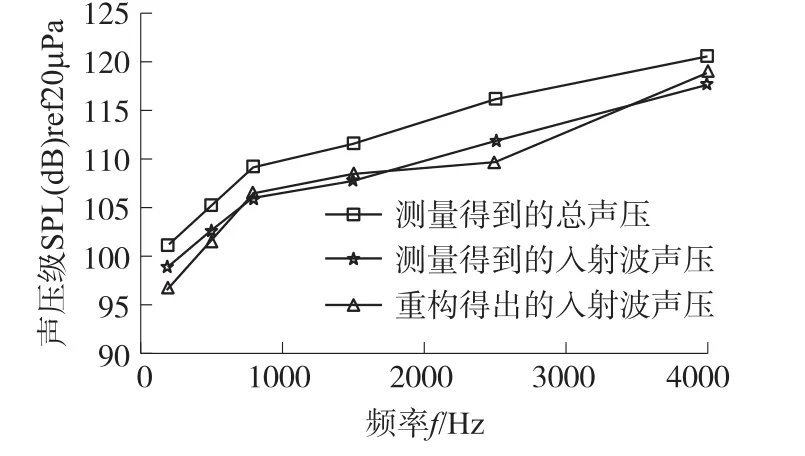
圖10 各頻率下，檢驗傳聲器位置處總聲壓、入射波聲場聲壓和重構的入射波聲場聲壓的比較（陣列半徑a=0.097 5 m，聲源離陣列中心距離d=0.13 m，傳聲器數目M=36）

由圖10可得，對于檢驗傳聲器位置處，總聲壓測量值與入射波聲場聲壓測量值均隨著頻率f的增大而增大，在各頻率下總聲壓測量值大于入射波聲場聲壓測量值，這符合第1.2節中的分析，因為檢驗傳聲器位于聲源與陣列之間的聲場區域。由于檢驗傳聲器位置處的總聲壓測量值與入射波聲場聲壓測量值分別為兩個實驗步驟下對應的測量值，因而兩者只能在幅值大小上進行比較，實驗結果為，在檢驗傳聲器位置處，各頻率下散射后的總聲壓級較散射前的入射波聲場聲壓級要大約4 dB左右，這說明聲源輻射的聲場在經過球形陣列散射后發生了較大的變化。同時，由圖10可得，在各頻率下，對于檢驗傳聲器位置處，聲場重構得出的入射波聲場聲壓級及與測量的入射波聲場聲壓級很接近，誤差在2 dB以內，這說明運用基于散射聲場模型的近場聲全息方法，可以以一定的精度重構出入射波聲場。其中，此誤差不僅僅是聲場重構計算方法引起的，其它影響誤差的因素主要有傳聲器測量誤差以及檢驗傳聲器坐標誤差等。

上述兩組實驗表明，采用剛性表面球形傳聲器陣列測得的總聲壓，基于考慮聲場散射的聲場模型和球面近場聲全息方法，可以重構出入射波聲場，消除由于球形陣列剛性表面散射造成的計算入射波聲場的誤差。

3 結論

本文通過應用剛性球體表面的聲波散射的數學模型，建立起聲場入射波聲壓與發生散射后總聲壓之間的關系。針對不同的波數，檢驗了球面波遇到剛性表面球體發生散射后，球體表面及外部空間聲場聲壓分布的變化規律。通過仿真與實驗檢驗了由剛性表面球形陣列上傳聲器測得的總聲壓，運用球面近場聲全息方法，在球形陣列表面及外部空間中入射波聲場重構的精度。得出如下結論：①剛性球體表面處聲壓分布在散射前與散射后發生了較大的變化，因而在入射波聲場重構時，需要在聲場建模中考慮剛性球面的聲波散射。②通過建立剛性球面對聲波散射的數學模型，并應用于球面近場聲全息方法中，可由剛性表面球形傳聲器陣列測量的總聲壓，實現入射波聲場的重構。在入射波聲場重構中，重構誤差會隨著重構半徑的增大而增大，在球形陣列外部的較近區域，能取得較高的重構精度。同時，在波數較大時，由于聲源近場信息衰減較快，重構誤差隨重構半徑增大而急劇增大；而在波數較小時，重構誤差隨重構半徑增大則較緩慢地增大，即使在重構半徑較大的情形下，重構誤差也相對較小。此外，當重構面為聲源所在球面時，即使在總的重構誤差較大的情形下，通過重構出的入射波聲壓分布圖，依然可以很好地識別出聲源的方位。

本文研究在多個方面還需要進一步研究：①本文以完全剛性球體的邊界條件，得出了聲波散射的聲場數學模型。但在實際中，剛性表面球形傳聲器陣列的球面上鑲嵌有多個傳聲器，在傳聲器位置波動方程解并不滿足剛性面散射的Neumann邊界條件。為提高入射波聲場的重構精度，需要考慮建立更精確的剛性表面球形傳聲器陣列的散射邊界條件模型。②在入射波聲場的重構中，由測量誤差或環境噪聲引起的微小誤差會在聲場重構逆向變換的過程中放大。引入如Tikhonov法或Landweber迭代法等正則化方法，可進一步提高入射波聲場的重構精度，由于論文篇幅的限制，本文沒有進行探討。

［1］Williams E G，Nicolas Valdivia，Peter C Herdic，et al.Volumetric Acoustic Vector Intensity Imager［J］.Journal of the Acoustical So?ciety of America，2006，120：1887-1897.

［2］Jacobsen F，Moreno G，Grande E F，et al.Near Field Acoustic Ho?lography with Microphones Mounted on a Rigid Sphere［C］//Pro?ceedings of Inter-Noise.2008.

［3］Williams E G，Takashima K.Vector Intensity Reconstructions in a Volume Surrounding a Rigid Spherical Microphone Array［J］.Jour?nal of the Acoustical Society of America，2010，127（2）：773-783.

［4］Jacobsen F，Moreno G，Grande E F，et al.Near Field Acoustic Ho?lography with Microphones on a Rigid Sphere［J］.Journal of the Acoustical Society of America，2011，129（6）：3461-3464.

［5］Lu H，Li M.Reconstruction of Sound Field Based on Near-Field Acoustic Holography with a Rigid Spherical Microphone Array［C］//Proceedings of the Hong Kong：ACOUSTIC 2012 Hong Kong Conference and Exhibition.2012：3258-3258.

［6］Hardin R H，Sloane N J A.McLaren’s Improved Snub Cube and other New Spherical Designs in Three Dimensions［J］.Discrete Computational Geometry，1995（15）：429-441.

［7］莫爾斯P M，英格德U.理論聲學［M］.楊訓仁，呂如榆，譯.北京：科學出版社，1984.

［8］杜功煥，朱哲民，龔秀芬.聲學基礎［M］.第3版.南京：南京大學出版社，2012.

［9］張海瀾.理論聲學［M］.北京：高等教育出版社，2007.

［10］褚志剛，楊洋，蔣忠翰.波束形成傳聲器陣列性能研究［J］.傳感技術學報，2011，24（5）：665-670.

［11］丁浩，李春曉，金江明，等.可識別聲源深度的三維聲聚焦波束形成方法［J］.傳感技術學報，2013，26（2）：175-181.

［12］劉夢然，張國軍，簡澤明，等.管道內檢測器聲定位技術研究［J］.傳感技術學報，2014，27（4）：500-504.

［13］Franz Zotter.Analysis and Synthesis of Sound-Radiation with Spherical Arrays［D］.Austria：Institute of Electronic Music and Acoustics University，2009.

［14］Lu Huancai.Reconstruction of Vibroacoustic Responses Using Helmholtz Equation Least-Squares Method［D］.Doctoral Disserta?tion，Detroit：Wayne State University，2007.

［15］Haddad K，Hald J.3D Localization of Acoustic Sources with a Spherical Array［J］.Journal of the Acoustical Society of America，2008，123（5）：3311-3311.

李敏宗（1988-），男，浙江工業大學博士研究生，主要研究方向為噪聲源識別定位及傳聲器陣列信號處理，limin?zong_svlab@163.com；

盧奐采（1962-），女，教授，博導，美國聲學學會會員，美國機械工程師學會會員，2007年于美國Wayne State Universi?ty獲得機械工程博士學位，1996年于浙江大學獲得工學博士學位，主要從事3D傳聲器陣列理論、聲全息理論及聲場可視化和聲學圖像處理等方面的研究，huancailu@zjut.edu.cn。

Reconstruction of Incident Sound Field and Identification of Sound Source Using a Rigid Spherical Microphone Array*

LI Minzong1，LU Huancai1，2*，JIN Jiangming1
（1.Key Laboratory of Equipment&Manufacturing，Ministry of Education&Zhejiang Province，College of Mechanical Engineering，Zhejiang University of Technology，Hangzhou 310014，China；2.Zhejiang Key Laboratory for Signal Processing，Zhejiang University of Technology，Hangzhou 310014，China）

Rigid spherical microphone array is an ideal measurement front-end for three-dimensional sound field re?construction.However，as the rigid surface of the array scatters incident sound waves，the directly measured pres?sures and near-field acoustic holography approach based on the math model of free field could not be employed to reconstruct the incident sound field.In this paper，the math model of scattered sound field based on Neumann boundary condition was applied；the relationship between the total sound pressure after scattering and the incident sound pressure was developed and analyzed.Then the incident sound field was reconstructed by using the input da?ta of measured total sound pressure with a rigid microphone array.The variation of sound pressure distribution on the surface of rigid sphere was examined through simulations and experiments.And the reconstruction accuracy was examined when the reconstruction parameters，such as frequency and reconstruction radius，varied.The reconstruc?tion results show that the incident sound field can be reconstructed with certain accuracy with a rigid spherical mi?crophone array，based on spherical near-field acoustic holography with the math model of scattered sound field.

spherical microphone array；reconstruction of incident sound field；spherical near-field acoustic holog?raphy；sound wave scattering；rigid surface sphere

TB877.2

A

1004-1699(2015)10-1459-08

??7320Q；7810

10.3969/j.issn.1004-1699.2015.10.007

項目來源：國家自然科學基金項目（51205354，51275469）；浙江省國際科技合作專項項目（2013C14014）

2015-03-12 修改日期：2015-08-12