基于禁忌搜索算法的聯賽調度問題求解研究

趙玉明

（肇慶學院 計算機學院，廣東 肇慶 526061）

0 引言

許多聯賽（例如足球，籃球，乒乓球）主管部門必須要面對參賽隊伍的調度問題.這些調度問題一般含有相互沖突的約束和不同的優化目標.例如：旅行距離最小[1]，每隊每天只有1場比賽，特殊日期體育場不能使用，主場比賽與其所對應的客場比賽之間天數最少，等等.求解滿足上述條件和優化目標的問題從而得到滿意的調度非常困難.

許多研究者為解決這類調度問題做了很多研究，提出了很多方法同時也取得了不同程度的成功，例如整數線性規劃[2]、約束規劃[3]、局部搜索（模擬退火算法[4]，禁忌搜索算法[5]，混合算法等）.

本文要解決的是一類特殊的聯賽調度問題（SLSP），McAloon等[6]研究過這類問題.他們使用整數線性規劃得到的結果很不理想；之后嘗試采用約束規劃，得到了較好的結果；最后用局部搜索算法得到和約束規劃相同的結果，但前者的計算時間要少得多.

Gomes 等[7]使用確定完整搜索的隨機版本求解SLSP 問題，取得的結果比使用約束規劃得到的結果要好，并且能解決參賽隊數目較大的問題.

Regin[8-9]提出2種使用約束規劃解決SLSP問題的方法.第1種方法使用強有力的過濾算法，得到的結果在執行時間和魯棒性方面都比文獻[6]和文獻[7]好.第2種方法是第1種方法的改進，這種改進基于問題的轉換.Regin通過引入一個隱式約束，把SLSP問題轉化成一個等價問題，然后使用一個啟發式的特殊過濾算法改進了其自己的結果.

本文的研究旨在提出一種基于禁忌搜索的局部搜索算法求解SLSP問題.

本文結構安排如下：第2 部分正式表述SLSP 問題；第3 部分為SLSP 問題建立約束滿足問題模型；第4部分提出我們的禁忌搜索算法；第5部分給出比較測試結果；第6部分總結全文并得出結論.

1 問題的描述

本文后面部分都使用下列約束和定義.

|T|支參賽隊，|T|為偶數，T 是所有參賽隊的集合；

所有參賽隊相互比賽且僅比賽1次；

整個賽季持續|T|-1個星期；

每支參賽隊每星期必須進行1次比賽；

每星期有|T|/2局比賽，一場比賽可以被安排在任一局比賽；

整個賽季1支參賽隊出現在同一局里面最多2次；

此調度問題就是在滿足上述約束的基礎上調度安排所有參賽隊.為了說明上述問題我們在表1中給出一個有8支參賽隊參賽，賽季長達7個星期，每個星期進行4局比賽的聯賽調度問題的可行調度.8支參賽隊以A～H作為標號.

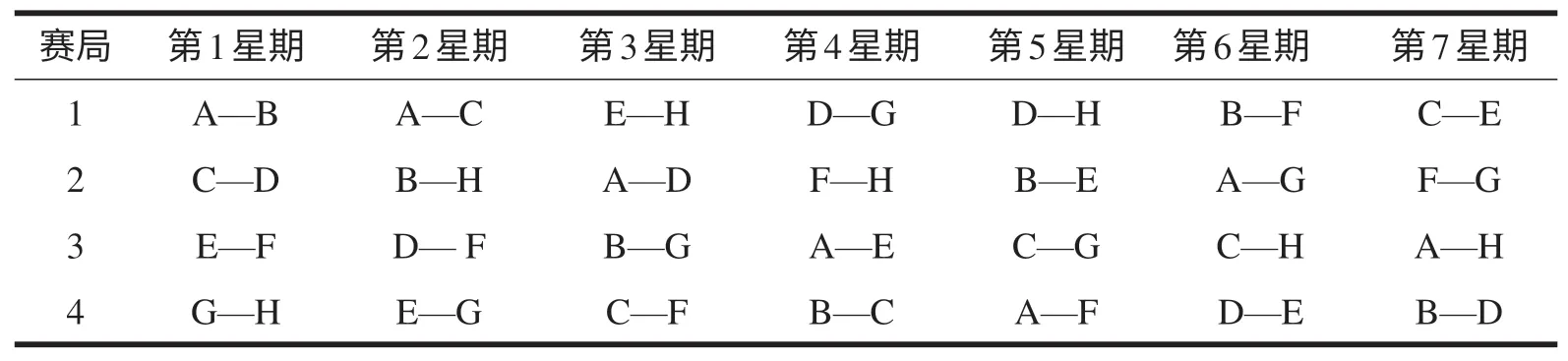
表1 含有8支參賽隊的一個可行調度

從表1可以看出，賽程的安排可以用二維數組表示，行用來表示第n 個星期，列用來表示賽局.每一列滿足基數約束，即每支參賽隊僅出現1次.在每行中每支參賽隊最多出現2次.另外每場比賽僅出現1次，即表1中所有比賽不同.

2 將問題公式化

我們把SLSP問題看作一個約束滿足問題，并使用約束規劃描述它.

2.1 約束滿足問題（CSP）

約束滿足問題用一個三元組（X,D,C）定義.

X 是含有n 個變量的有限集：X={X1,…,Xn};

D 是相關域的集合：D={D1,…,Dn}，每一個Di是由Xi的所有可能的取值組成的有限集.

C 是p 個約束組成的集合：C={C1,…,Cp}，每個約束定義在一個變量集合上，同時確定哪些取值組合與變量取值一致.

給定上述三元組后，CSP問題本質上是在所有變量取值范圍內尋找滿足所有約束的全部變量值，這些變量值被稱為符合CSP問題.所有變量取值的集合定義成域的笛卡爾積D1×…×Dn，求解CSP問題意味著在巨大數目的可能變量取值里尋找一個特殊的滿足約束的變量值.

2.2 SLSP問題公式化成CSP問題

使用下列符號將SLSP問題描述成CSP問題：

P:局集合，|P|=|T|/2;

W:星期集合，|W|=|T|-1;

tn:第n 個參賽隊編號，tn∈T,1≤n≤|T||;

x(tm,tn):tm—tn比賽的調度變量，其值的形式為(pm,n,wm,n)，意味著此次比賽被安排到wm,n星期pm,n局.

很明顯X={x(tm,tn),1≤m≤n≤|T|},并且所有的域都等于D={(pm,n,wm,n),pm,n∈p,1≤pm,n≤|P|,wm,n∈W,1≤wm,n≤|W|};?x ∈X,Dx=Do.約束集C 包含下列3種約束：

唯一性約束，即每支參賽隊每星期只進行1 場比賽.Constraint 1(tn)?wm,n≠wq,n,?(m,q)∈[1；|T|]2,m≠n,q≠n,m≠q;

每支參賽隊在同一局不能多于1 場比賽約束.Constraint 2(tn)?|pm,n=pqn,(m,q)∈[1；|T|]2,m≠n,q≠n,m≠q}|≤1；

所有比賽不同約束.Constraint 3(tm,tn)?tm,tn≠tq,tr,?tq,tr∈T2,tq≠tr.

3 使用禁忌搜索求解SLSP問題

3.1 搜索空間

賽程安排就是域D={(pm,n,wm,n,pm,n∈p,1≤pm,n≤|P|,wm,n∈W,1≤wm,n≤|W|}中的元素對變量集合X={x(tm,tn),1≤m＜n≤|T|}中所有變量進行完全賦值.因此賽程安排是一個大小為|W|×|P|的二維表，表中元素是二元組(m,n),1≤m＜n≤|T|.對于有40個參賽隊的SLSP問題有780個變量，每個變量有780個值.

一共有|T|/2×(|T|-1)場比賽需要調度，每個調度可以看成是對所有比賽的一個排列.有|T|個參賽隊的SLSP問題，其搜索空間的大小是(|T|/2×(|T|-1))!.

3.2 初始賽程安排

初始賽程安排用來指定搜索空間的起點，可以隨意指定一個滿足Constraint 3的賽程安排作為搜索空間的起點，然后隨意為每個二元組(w,p)安排1場比賽，w ∈W,p ∈P.受文獻[10]的啟發，筆者采用另一種方式構建初始賽程安排.限于篇幅構建過程省略，具體步驟可參見文獻[10].筆者所構造的初始賽程安排滿足Constraint 1和Constraint 3.

3.3 鄰域

設s 為一來自搜索空間S 的賽程安排，s 的鄰域N(s)定義如下：

N(s)={s′|s′∈S,s和s′只有一對變量值不同,并且s和s′中至少有一個不滿足約束}.s 的鄰域可以通過交換當前s 中任意不滿足約束的2 個變量的當前值得到.我們可以用二元組表示從賽程安排s 到s的鄰域s′ 的一次移動，也就是交換2 場比賽.另外，為了保證滿足Constraint 2，交換比賽應在同一個星期進行.

3.4 評估函數

為了比較賽程安排的質量，定義一個評估函數f(s).令Happ Ps(p,tn)為賽程安排s 中參賽隊tn出現在賽局p 的次數.f(s)為所有參賽隊在所有賽局里出現次數最多的總和.

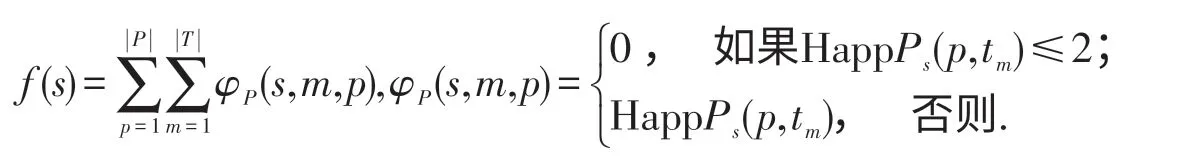
解SLSP問題本質上就是找到一個賽程安排ξ ∈S，使得f(ξ)=0 成立.

3.5 禁忌表管理

禁忌表是特殊的短期記憶，包含由曾經遇到的賽程安排或這些賽程安排的有關屬性，是禁忌搜索的基本組成部分.設立禁忌表的目的是避免陷入死循環和跳出局部最優狀態.禁忌期限對禁忌算法的性能有很大影響，期限過長會限制對沒有探索的賽程安排的訪問，并且禁忌算法探索鄰域的能力會減弱；期限過短會使禁忌算法限于局部最優的狀態.

在嘗試了不同的禁忌期限后，筆者選擇使用隨機禁忌期限.賽程安排s 的禁忌期限定義如下：ks=rand(g)，rand(g)是一個[1;g]之間的隨機整數，g ∈[10;80]，s ∈S.用|X|×|X|的矩陣實現禁忌表，矩陣的每個元素對應于一次移動，并且存儲了當前迭代次數和禁忌期限.使用這種數據結構，通過簡單的當前迭代次數比較就可以知道一個移動是否是合法的.

3.6 通用算法

本文所提出的TS-SLSP 算法以構建滿足Constraint 1 和Constraint 3 的搜索空間初始賽程安排作為開端，而后沿著鄰域繼續迭代訪問一系列局部最好的賽程安排.在每次迭代中，最好的移動即使不能改善當前賽程安排的評估函數值，也會被用于當前賽程安排.如果f(x)=0,即找到一個最優的調度或者移動次數達到給定的限制，算法停止.TS-SLSP算法的偽代碼如下：

輸入：||T；

輸出：最優賽程安排或者找不到最優賽程安排；

f 為評估函數，f′為該評估函數的當前最優值；

c 為當前賽程安排，c′為迄今所遇到的最好賽程安排；

第1步：初始化禁忌表為空；

第2步：產生初始賽程安排c；

第3步：c′=c;

第4步：f′=f(c);

第5步：如果滿足算法停止條件，到第11步；

第6步：對c 做最好的移動m,把m 添加到禁忌列表；

第7步：如果f(s)＜f′,c′=c,f′=f(c),到第5步;否則到第8步；

第8步：如果f′在足夠時間內沒有被改善，c=c′,禁忌表清空，去第5步；

第9步：如果f′=0，找到最優賽程安排，到第11步；

第10步：輸出：找不到最優賽程安排；

第11步：算法終止.

4 計算結果

將本文提出的禁忌算法同文獻[9]中的算法進行比較測試，結果如表2所示.測試在Windows XP操作系統下進行，系統配置3.33 Gb內存，3.39 MHz.測試用例從14個參賽隊到41個參賽隊.本文提出的TS-SLSP算法允許進行2 000萬次迭代.

從表2可以看出，同文獻[9]中的算法相比，本文提出的算法有如下優點：第一，具有很強的求解能力.在參賽隊數目大于28時，文獻[9]中的算法在2 h內已經不能找到解，而TS-SLSP算法在參賽隊數目高達40的情況下仍然可以找到最優賽程安排，盡管運行時間延長很多.第二，具有很高的成功率.在參賽隊數目小于25時，本文提出的算法成功率都大于85%，甚至達到100%.從表2也可看到本文提出算法存在的不足：第一，在參賽隊數目小于28時，本文提出的算法比文獻[9]中算法運行的時間長；第二，在參賽隊數目為41時，本文提出的算法在2 h內迭代2 000萬次的情況下找不到解；第三，算法的成功率隨著參賽隊數目的增加而降低.

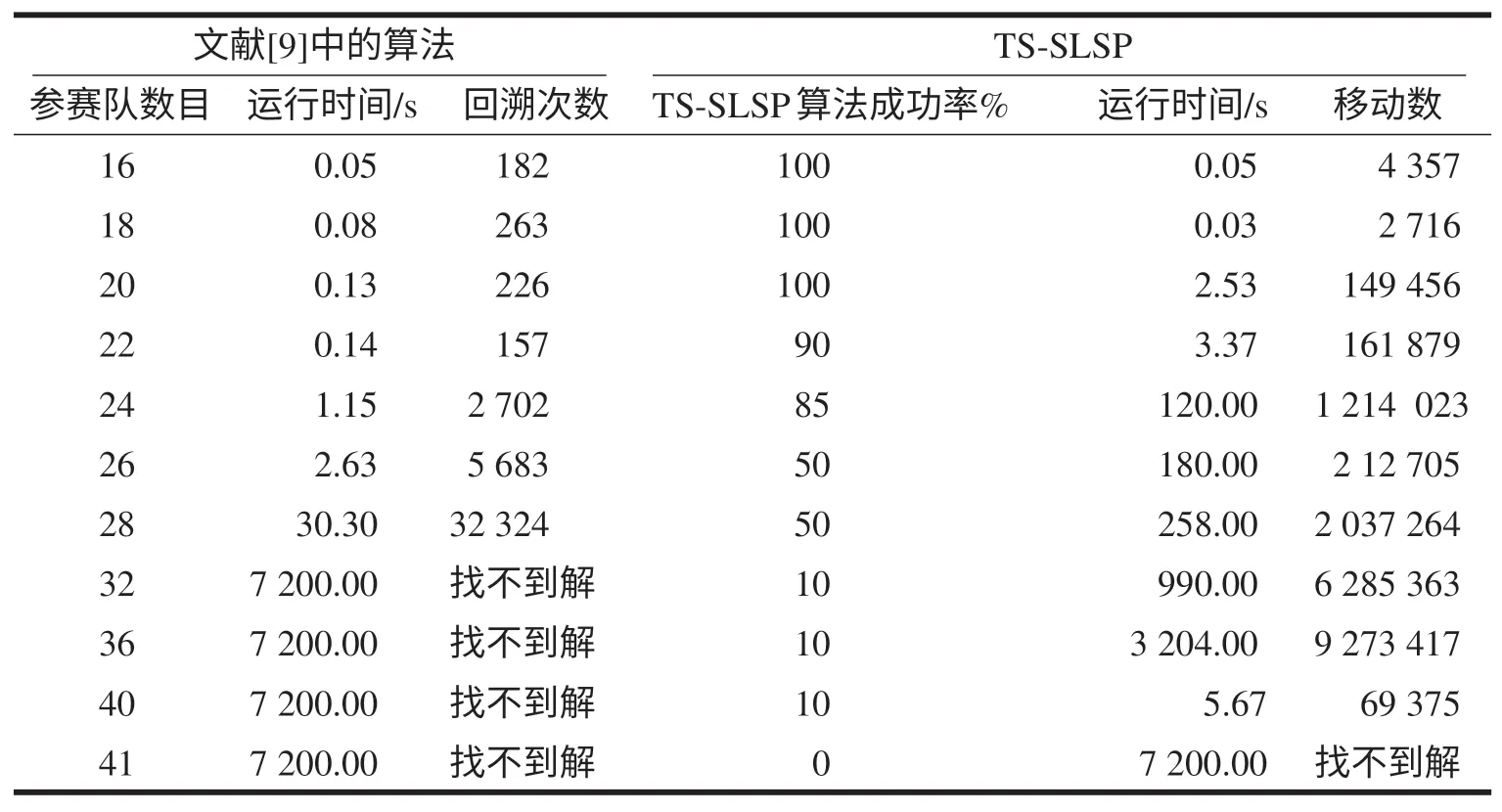
表2 比較測試結果

5 結論

本文中，筆者為聯賽調度問題提出一種禁忌算法（TS-SLSP），該算法基于SLSP問題的CSP形式且具有以下特性：簡單的交換鄰域，便于快速鄰域搜索的高效數據機構，動態禁忌期限等.測試結果表明TS-SLSP算法在求解能力方面優于文獻[9]中的算法，盡管文獻[9]中的算法組合了約束傳遞算法和原始問題的非平凡形式.同時，我們注意到TS-SLSP算法的運行時間遠大于文獻[9]中的算法，這也說明本文提出的算法有很大的改進空間.例如：可以將約束傳遞技術同禁忌搜索結合起來提高算法的效率，這將是今后的研究方向之一.

本文的工作再一次證明了高效數據結構對禁忌搜索算法性能的重要性，同時也證實了參數的設置對于獲得高質量的解具有關鍵性作用.可以將TS-SLSP算法做一些調整以解決其他的運動調度優化問題，例如最小化主客場比賽時間間隔.所有這些研究表明，元啟發式算法（禁忌搜索算法，模擬退火算法等）對解決各種計劃和調度問題具有較好的潛力.

[1]BEAN J C,Brige J R.Reducing traveling costs and player fatigue in the national basketball association[J].Interfaces,1980,10(3):98-102.

[2]FERLAND J A,FLEURENT C.Allocating games for the NHL using integer programming[J].Operations Research,1996,41(4):649-654.

[3]HENZ M.Scheduling a major college basketball conference[J].Operations Research,2001,49(1):649-654.

[4]TERRI B J,Willis R J.Scheduling the australian state cricket season using simulated annealing[J].Journal of the Operational Research society,1994,45(3):276-280.

[5]WRIGHT M.Timetabling county cricket fixtures using a form of tabu search[J].Journal of the Operational Research Society,1994,45(7):758-770.

[6]MCALOON K,TRETKOFF C,WETZEL G.Sports league scheduling[C]//Proceedings of the Third ILOG Optimization Suite International Users’Conference.1997.

[7]GOMES C P,SELMAN B,KAUTZ H A.Boosting combinatorial search through randomization[C]//Proceedings of the Fifteenth National Conference on Artificial Intelligence.Madison:AAAI Press,1998:431-437.

[8]REGIN J C.Modeling and solving sports league scheduling with constraint programming[C]//First Congress of the French Operational Research Society.1998.

[9]REGIN J C,Sports scheduling and constraint programming[C]//INFORMS.1999.

[10]SCHREUDER J A M.Constructing timetables for sport competitions[J].Mathematical Programming Study,1980,13:58-67.