ARIMA模型在基坑變形監測中的應用

王沈力，賁柯

（甘肅中建市政工程勘察設計研究院，甘肅 蘭州 730000）

1 概 述

為了檢測巖土基坑的穩定性，變形監測是必不可少的。變形監測是為工程建設的可行性評估以及后期運營提供數據資料。時間序列分析是一種動態的數據處理方法，其特點在于各個觀測值之間通常是不獨立的，未來數據可以由當前以及過去數值來預測，可以利用觀測數據之間的自相關性建立相應的數學模型來描述客觀現象的動態特征。本文針對蘭州某基坑變形監測資料進行分析,采用時間序列分析建模，主要采用ARIMA模型，再利用Eviews6.0實現建模過程，最終得出該方法處理的模型。

ARIMA模型的基本思想是：將預測對象隨時間推移而形成的數據序列視為一個隨機序列，用一定的數學模型來近似描述這個序列。這個模型一旦被識別后就可以從時間序列的過去值及現在值來預測未來值。

對于平穩、正態、零均值的時間序列Xt｛｝(t=1,2,···n)，若Xt不僅與前n 步的各個取值xt-1,xt-2,xt-n有關，還與前m 步的干擾at-1,at-2,at-m有關，因此可得到最一般的ARMA模型：

其中φ1(i=1,2,···n)稱為自回歸參數，稱為滑動平均參數，為白噪聲序列。式（1）稱為自回歸滑動平均模型，記為ARMA（n，m）模型。而ARIMA（p，d，q）模型實質上先對觀測數據進行d次差分處理，然后再擬合ARMA（p，q）模型。

2 ARIMA模型建模的步驟

2.1 平穩性檢驗

根據時間序列的散點圖、自相關函數和偏自相關函數圖以及ADF單位根檢驗其方差、趨勢及其季節性變化規律，對序列的平穩性進行識別。一般來講，大部分時間序列都不是平穩序列。

2.2 平穩化處理

對于非平穩的時間序列，我們通常用差分法進行處理，以達到平穩化。一般來講，一階差分可以消除線性趨勢，二階差分可以消除二次曲線趨勢。重復進行差分，直至成為平穩序列。此時，差分的次數即為ARIMA（p，d，q）模型中的階數d。從理論上講足夠多次的差分運算可以充分提取序列中的非平穩確定性信息，但也應當避免過度差分，防止消除原序列的長期特征，丟失某些信息。實際的時間序列差分階數d一般不超過2。

2.3 模型定階

根據時間序列模型的識別規則，建立相應的模型。若平穩序列的偏相關函數是截尾的，而自相關函數是拖尾的，可斷定序列適合AR模型；若平穩序列的偏相關函數是拖尾的，而自相關函數是截尾的，則可斷定序列適合MA模型；若平穩序列的偏相關函數和自相關函數均是拖尾的，則序列適合ARMA模型。

2.4 參數估計

Eviews6.0中常用的估計方法有矩估計、極大似然估計和最小二乘估計，以此來檢驗模型是否具有統計意義。

2.5 模型檢驗

對所建立模型的殘差進行檢驗，得到殘差的自相關圖和偏自相關圖，診斷殘差序列是否為白噪聲。

2.6 預測

利用已通過檢驗的模型進行預測分析。

3 實例分析

3.1 工程概況

根據蘭州某基坑工程進展情況，于2013年12月17日對該基坑工程進行第一次沉降變形觀測，截至2014年03月27日第37次觀測為止。基坑沉降變形觀測點按國家一等水準測量精度要求進行施測，測站觀測采用光學測微法，視線長度≤50m,前后視距差≤1m,視線高度≥0.2m，水準觀測的限差符合基輔分劃讀數之差0.5mm,高差之差為0.7mm,往返較差及環線閉合差≤1.0mm（n為測站數）。沉降觀測每次采用固定人員司儀、記錄，設備采用徠卡DNA03電子水準儀，標尺采用3.0米條碼標尺。每次作業前已對水準儀的i角及水準尺的水準器進行檢查。

3.2 時間序列分析

為了反映基坑的沉降變化趨勢，我們選取10個不同的點進行監測。本文僅列出1號點位不同時期的觀測量,表1為1號點位不同時期觀測數據。

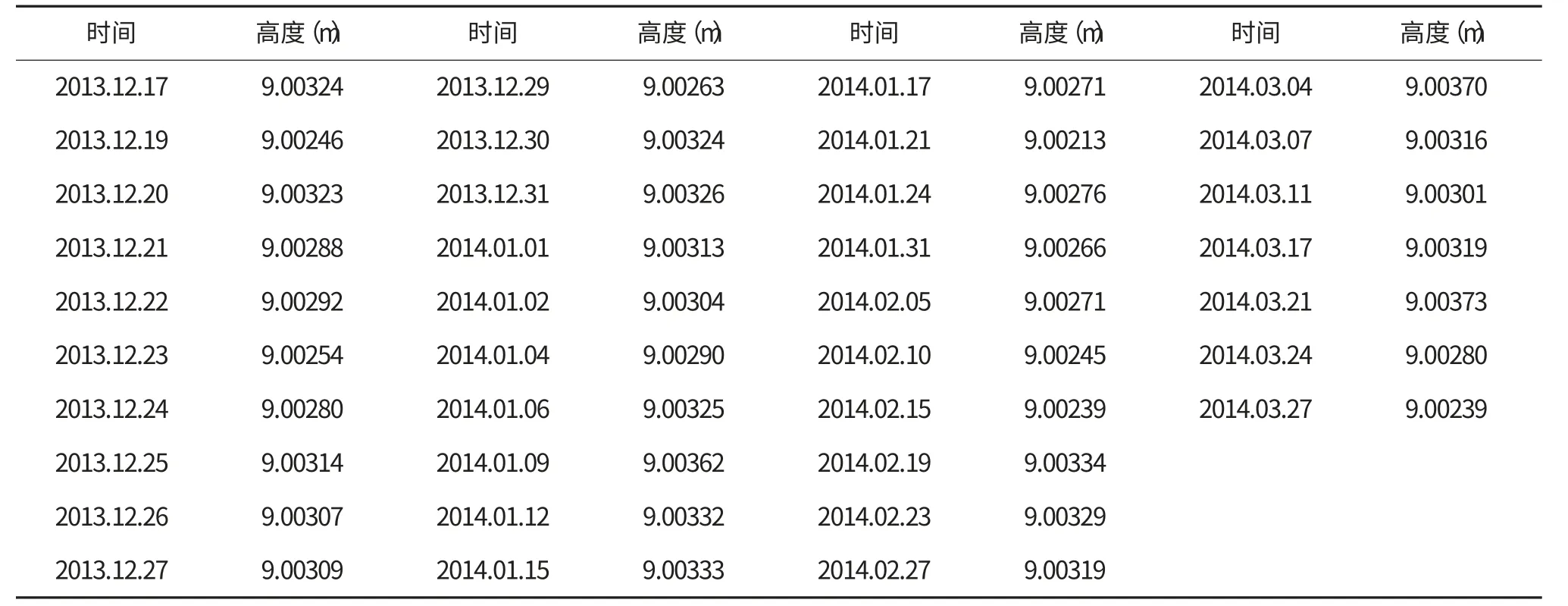
1號點位不同時期觀測數據 表1

3.2.1 平穩性

由圖1可知該序列是不平穩序列。

圖1 1號點的原始序列圖

3.2.2 平穩化處理

由于原始序列不是平穩序列，因此需對其進行1階差分，得到圖所示的折線圖。從圖2可看出，該序列是寬平穩過程，并且實現了零均值。

3.2.3 模型定階

圖2 1號點1階差分后的序列圖

1階差分后的折線圖滿足了平穩、零均值化條件,計算該序列的自相關系數和偏自相關系數如圖3所示。從圖中可看出ACF與PACF都在延遲大概二階后，基本控制在兩個標準差范圍之內，可認為該序列在零軸附近波動，具有短期相關性，同時可認為該序列為平穩隨機序列，故可構造ARIMA（2,1,2）模型。

3.2.4 參數估計

這里我們采用最小二乘估計，估計參數結果如圖4所示。

圖3 自相關系數和偏自相關圖

圖4 參數估計結果圖

3.2.5 模型檢驗

對此模型的殘差進行檢驗，得到殘差的自相關圖和偏自相關圖，可知模型的殘差基本都在置信區間范圍內，可認為與0無明顯差異，已基本上消除了自相關和偏自相關，表明殘差序列是獨立的。綜合上述分析可以得出結論，利用ARIMA（2,21,2）模型是合適的。

3.3 結果分析

根據用Eviews6.0擬合好的模型—ARIMA（2,1,2）模型,對原始數據進行預測，結果如表2所示。

經過對基坑工程10個監測點沉降變形，表2列出了1號點從2014年2月19日到2014年3月27日共10個觀測值的實際值、預測值以及他們之間的差值,其差值的絕對值均在0.6mm之內,說明預測值能達到較高的精度,達到了令人滿意的結果。

1號點的預測值與實際觀測值比較 表2

4 結 論

①在基坑沉降變形監測中應用時間序列分析模型進行建模,具有良好的效果,但隨著時間的推移，預測精度會逐漸降低,因此需要根據實際監測數據進行動態建模以避免預測結果失真。

②時間序列預測ARIMA模型在變形監測中具有良好的短期預測效果,只需對觀測序列進行動態的建模,就可以實時掌握基坑施工過程中的變形情況,確保工程施工和運營的安全。

[1]張曉峒.EVIEWS使用指南與案例[M].北京：機械工業出版社，2007.

[2]何書元.應用時間序列分析[M].北京：北京大學出版社，2003.

[3]張曉峒.計量經濟分析[M].北京：經濟科學出版社，2000.

[4]薛冬梅.ARIMA模型及其在時間序列分析中的應用[J].吉林化工學院學報，2010(3).

[5]張麗.天津市人均GDP時間序列模型及預測[J].區域經濟，2007(3).

[6]劉燕萍.時間序列分析在建筑物變形監測中的應用[J].勘察科學技術，2010(6).