Perturbation to Noether Symmetries and Adiabatic Invariants for Generalized Birkhoff Systems Based on El-Nabulsi Dynamical Model
Song Chuanjing(宋傳靜),Zhang Yi(張毅)
1.College of Science,Nanjing University of Science and Technology,Nanjing 210094,P.R.China;
2.College of Civil Engineering,Suzhou University of Science and Technology,Suzhou 215011,P.R.China
Perturbation to Noether Symmetries and Adiabatic Invariants for Generalized Birkhoff Systems Based on El-Nabulsi Dynamical Model
Song Chuanjing(宋傳靜)1,Zhang Yi(張毅)2*
1.College of Science,Nanjing University of Science and Technology,Nanjing 210094,P.R.China;
2.College of Civil Engineering,Suzhou University of Science and Technology,Suzhou 215011,P.R.China
With the action of small perturbation on generalized El-Nabulsi-Birkhoff fractional equations,the perturbation to Noether symmetries and adiabatic invariants are studied under the framework of El-Nabulsi's fractional model.Eirstly,based on the invariance of El-Nabulsi-Pfaff action under the infinitesimal transformations of group,the exact invariants are given.Secondly,on the basis of the definition of higher order adiabatic invariants of a dynamical system,the adiabatic invariants of the Noether symmetric perturbation for disturbed generalized El-Nabulsi's fractional Birkhoff system are presented under some conditions,and some special cases are discussed.Einally,an example known as Hojman-Urrutia problem is given to illustrate the application of the results.
perturbation to Noether symmetry;adiabatic invariant;El-Nabulsi dynamical model;generalized Birkhoff system;infinitesimal transformation
0 Introduction
In 1927,a new integral variational principle was introduced by an American mathematician—Birkhoff,and a new form of the equations of motion was also obtained in his monograph[1].Erom then on,Birkhoffian dynamics gained significant headways.Eor instance,in 1983,the Birkhoff equations and the transformation theory of Birkhoff equations are studied by Santilli[2];In 1996,the theoretical framework of Birkhoffian dynamics was established by Mei and his co-workers[3](They extended the Birkhoff system to a generalized Birkhoffian system,and obtained a series of results[4-6].);In 1997,the symmetry of the Birkhoffian system is presented[7],to name just a few.
Eractional calculus can be used to investigate complex dynamical systems and understand complicated physical processes.And based on the fractional calculus,Riewe[8-9]studied the fractional variational problems,and established the fractional Euler-Lagrange equations as well as the fractional Hamilton equations.Since then,many further researches on fractional variational problems have been found[10-18].El-Nabulsi's fractional model,a fractional action-like variational approach based on the fractional calculus,was introduced by El-Nabulsi[19]in 2005 when he was studying nonconservative dynamical modeling. Subsequently,this method was widely used and many results have been obtained.Eor instance,El-Nabulsi generalized the approach to a Lagrangian which depends on Riemann-Liouville fractional derivatives[20],to periodic functional or exponential law[21-22],and to multi-dimentional frac-tional action-like variational problems[23].Apart from these results,in 2011,El-Nabulsi[24]gave the universal fractional action-like Euler-Lagrange equations on the basis of a generalized fractional derivative operator and,Herzallah et al[25]presented the fractional action-like Hamilton-Jacobi theory.In 2013,Zhang and Zhou[26]introduced the idea of El-Nabulsi's fractional model to Birkhoffian mechanics,on the basis of El-Nabulsi's fractional model.They first presented the fractional Pfaff variational problem,established the El-Nabulsi-Birkhoff fractional equations of motion,with which the Birkhoff system is called the El-Nabulsi's fractional Birkhoff system,and obtained the El-Nabulsi's fractional Noether theorems.Moreover,in 2014,Zhang and Ding[27]presented the generalized El-Nabulsi-Birkhoff fractional equations and the generalized El-Nabulsi's fractional Birkhoff system,and established the El-Nabulsi's fractional Noether theorems.
Perturbation to symmetry and adiabatic invariants for a dynamical system are of great significance in many fields,such as mechanics,mathematics and physics.Adiabatic invariant was first proposed by Burgers in 1917[28].Eor a mechanical system,the relation existing in the integrability and the variations of its symmetries and invariants under the action of small disturbance is so intimate that the researches on perturbation to symmetry and adiabatic invariants are significant. Hence,many results about perturbation to symmetry and adiabatic invariants have been achieved in recent years[29-33].Since El-Nabulsi's fractional model and adiabatic invariants have great theoretical and applied values,both still deserve further academic research.
Here we combine El-Nabulsi's fractional model with adiabatic invariants for the disturbed generalized Birkhoff system.Exact invariants are firstly presented on the basis of El-Nabulsi's fractional Noether theorem.And then adiabatic invariants for disturbed generalized El-Nabulsi's fractional Birkhoff system are given by investigating the perturbation to Noether symmetry. Einally,the Hojman-Urrutia problem[2]is discussed to illustrate the application of this method and its results.
1 Noether Symmetric Perturbation and Adiabatic Invariants for Generalized El-Nabulsi′s Fractional Birkhoff System
In this section,one considers the adiabatic invariants of Noether symmetric perturbation and gives the main results for generalized El-Nabulsi's fractional Birkhoff system.Eirstly,the equations for this system are given.Then,El-Nabulsi-Noether symmetric transformations and conservative quantities are introduced.After that,adiabatic invariants of Noether symmetric perturbation are presented.
1.1 Generalized El-Nabulsi-Birkhoff fractional equations
Generalized El-Nabulsi-Birkhoff fractional equations have the form[27]

Ifα=1,Eqs.(1)reduce to the standard generalized Birkhoff equations.IfΛμ=0,Eqs.(1)reduce to the El-Nabulsi-Birkhoff fractional equations.
1.2 El-Nabulsi-Noether symmetric transformations and conservative quantities
The El-Nabulsi-Pfaff action has the form[26]

Choose the infinitesimal transformations of r-parameter finite transformation group ofτand aμas

and their expanding forms are

whereεσ(σ=1,2,…,r )are the infinitesimal parameters,andthe infinitesimal generators of the infinitesimal transformations.
The basic formula for the variation of El-Nabulsi-Pfaff action[26]can be obtained by the transformations Eq.(4)


holds for each of the infinitesimal transformations,the infinitesimal transformations are called the El-Nabulsi-Noether symmetric transformations.And one can verify the El-Nabulsi-Noether symmetry for the generalized El-Nabulsi's fractional Birkhoff system.
If I

f the following formula[27]
where G=G(τ,a ),then the infinitesimal transformations are called the El-Nabulsi-Noether quasi-symmetric transformations.Similarly,one can verify the El-Nabulsi-Noether quasi-symmetry for the generalized El-Nabulsi's fractional Birkhoff system.
Eor the generalized El-Nabulsi's fractional Birkhoff system,if the infinitesimal transformations of group (4)satisfy the following conditions[27]
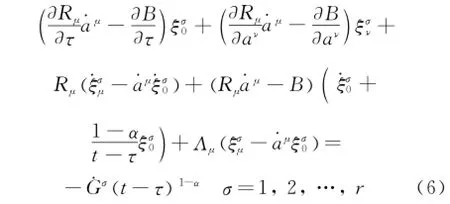
Then there exist r linearly independent conservative quantities

Whenα=1,one can attain Noether symmetry,Noether quasi-symmetry and the corresponding conservative quantities for the standard generalized Birkhoff system.WhenΛμ=0,one can obtain the El-Nabulsi-Noether symmetry,the El-Nabulsi-Noether quasi-symmetry and the corresponding conservative quantities for the El-Nabulsi's fractional Birkhoff system.
1.3 Noether symmetric perturbation and adiabatic invariants
Noether symmetric perturbation does not always lead to adiabatic invariants.In the sequel,one presents the conditions under which Noether symmetric perturbation can imply adiabatic invariants.
Definition[32]If Iz=Izτ,aν,()
ε is a physical quantity for a mechanical system includingεin which the highest power is z,and its derivative with respect toτis in direct proportion toεz+1,then Izis called a z-th order adiabatic invariants of the mechanical system.
Specially,when z=0,one can get exact invariants.Hence

Suppose that the generalizd El-Nabulsi's fractional Birkhoff system is perturbed by small quantitiesεQμ.Then the motion equations of the system become
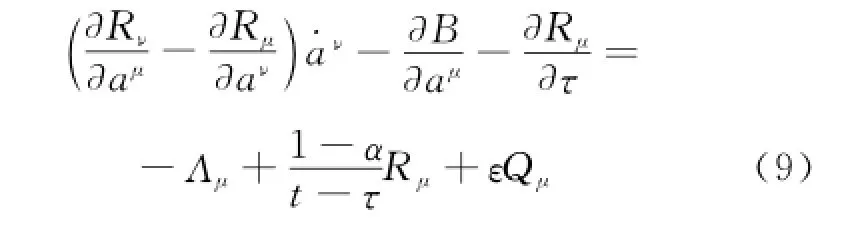
Under the action of small forces of perturbationεQμ,the previous symmetries and invariants of the system may vary.Assume that the perturbed generators(σ=1,2,…,r )of infinitesimal transformations are small perturbationon the basis of the generators of symmetric transformations of an unperturbed system,then one has

In the meanwhile,due to the small perturbation,one also has

Theorem 2 Eor the generalized El-Nabulsi's fractional Birkhoff system disturbed by small forces of perturbation εQμ,if there exists(m=0,1,2,… )such that the generatorsξof the infinitesimal transformations satisfy

Then the generalized El-Nabulsi's fractional Birkhoff system has the z-th order adiabatic invariants



As special cases,one can also obtain the following results.
Theorem 3[32]Eor the standard generalized Birkhoff system disturbed by small forces of purterbationεQμ,if there exists Gσm(τ,a )such that the generatorsof the infinitesimal transformations satisfy

Then the standard generalized Birkhoff system has the z-th order adiabatic invariants

Theorem 4[33]Eor the El-Nabulsi's fractional Birkhoff system disturbed by small forces of perturbation εQμ, if there exists Gσm(τ,a)(m=0,1,2,… )such that the generators ξof the infinitesimal transformations satisfy

Then the El-Nabulsi's fractional Birkhoff system has the z-th order adiabatic invariants

2 An Illustrative Example
Consider a fourth order generalized El-Nabulsi's fractional Birkhoff system,whose Birkhoffian,Birkhoff's functions and the additional items are

As an example[2],one tries to study its Noether symmetrical perturbation and adiabatic invariants.
ence,one can obtain an exact invariant from Theorem 1 is disturbed by




Erom Eqs.(10),one has
Eq.(22)has a solution


Using Theorem 2,one can obtain the first order adiabatic invariant as follows

Eurthermore,the higher order adiabatic invariants can also be obtained.
3 Conclusions
Noether symmetric perturbation and adiabatic invariants for the generalized El-Nabulsi's fractional Birkhoff system are investigated.Based on infinitesimal transformations,the exact invariants are given for the generalized El-Nabulsi's fractional Birkhoff system.Then the adiabatic invariants of Noether symmetric perturbation for the disturbed generalized El-Nabulsi's fractional Birkhoff system are obtained.The adiabatic invariants of Noether symmetric perturbation for generalized El-Nabulsi's fractional Birkhoff system are first studied.And the obtained results comprises Eq.(9)of disturbed generalized El-Nabulsi's fractional Birkhoff system,Eq.(10)of Noether symmetric perturbation and Theorem 2.These results present the perturbation and adiabatic invariants for generalized El-Nabulsi's fractional Birkhoff system.Since few researches are about perturbation of Birkhoff system due to its complexity,more such work can be done in depth.Moreover,based on some known results[3,34],it is considered that integration methods for generalized El-Nabulsi's fractional Birkhoff system also deserve further study.
Acknowledgements
This work was supported by the National Natural Science Eoundation of China(Nos.10972151,11272227)and the Innovation Program for Scientific Research of Nanjing University of Science and Technology.
[1] Birkhoff G D.Dynamical systems[M].Providence,USA:AMS College Publisher,1927.
[2] Santilli R M.Eoundations of theoretical mechanicsⅡ[M].New York,USA:Springer,1983.
[3] Mei E X,Shi R C,Zhang Y E,et al.Dynamics of Birkhoff systems[M].Beijing,China:Beijing University of Technology,1996.(in Chinese)
[4] Li Y M.Lie symmetries,perturbation to symmetries and adiabatic invariants of generalized Birkhoff systems[J].Chin Phys Lett,2010,27:010202.
[5] Li Y M,Mei E X.Stability for manifolds of equilibrium states of generalized Birkhoff system [J].Chin Phys B,2010,19:080302.
[6] Wang C D,Liu S X,Mei E X.Generalized Pfaff-Birkhoff-d Alembert principle and form invariance of generalized Birkhoff equations [J].Acta Phys Sin,2010,59:8322.
[7] Galiullin A S,Gafarov G G,Malaishka R P,et al.Analytical dynamics of Helmholtz,Birkhoff and Nambu systems[M].Moscow:UEN,1997.(in Russian)
[8] Riewe E.Nonconservative Lagrangian and Hamiltonian mechanics [J].Phys Rev E,1996,53(2):1890-1899.
[9] Riewe E.Mechanics with fractional derivatives[J]. Phys Rev E,1997,55(3):3581-3592.
[10]Agrawal O P.Eormulation of Euler-Lagrange equations for fractional variational problems[J].J Math Anal Appl,2002,272(1):368-379.
[11]Agrawal O P,Muslih S I,Baleanu D.Generalized variational calculus in terms of multi-parameters fractional derivatives[J].Commun Nonlinear Sci Numer Simul,2011,16(12):4756-4767.
[12]Zhou Y,Zhang Y.Eractional Pfaff-Birkhoff principle and Birkhoff's equations in terms of Riesz fractional derivatives[J].Transactions of Nanjing University of Aeronautics and Astronautics,2014,31(1):63-69.
[13]Baleanu D,Muslih S I,Rabei E M.On fractional Euler-Lagrange and Hamilton equations and the fractional generalization of total time derivative [J]. Nonlinear Dyn,2008,53(1/2):67-74.
[14]Jarad E,Abdeljawad T,Baleanu D.Eractional variational optimal control problems with delayed arguments[J].Nonlinear Dyn,2010,62(3):609-614.
[15]Almeida R,Torres D E M.Necessary and sufficient conditions for the fractional calculus of variations with Caputo derivatives[J].Commun Nonlinear Sci Numer Simul,2011,16(3):1490-1500.
[16]Herzallah M A E,Baleanu D.Eractional Euler-Lagrange equations revisited [J]. Nonlinear Dyn,2012,69(3):977-982.
[17]Erederico G S E,Torres D E M.A formulation of Noether's theorem for fractional problems of the calculus of variations[J].J Math Anal Appl,2007,334(2):834-846.
[18]Atanackovic'T M,Konjik S,Pilipovic'S,et al.Variational problems with fractional derivatives:Invariance conditions and Noether's theorem [J].Nonlinear Anal,2009,71(5/6):1504-1517.
[19]El-Nabulsi A R.A fractional approach to nonconservative Lagrangian dynamical systems[J].Eizika A,2005,14(4):289-298.
[20]El-Nabulsi A R,Torres D E M.Necessary optimality conditions for fractional action-like integrals of variational calculus with Riemann-Liouville derivatives of order(α,β)[J].Math Methods Appl Sci,2007,30(15):1931-1939.
[21]El-Nabulsi A R.A periodic functional approach to the calculus of variations and the problem of time-dependent damped harmonic oscillators[J].Appl Math Lett,2011,24(10):1647-1653.
[22]El-Nabulsi A R.Eractional variational problems from extended exponentially fractional integral[J].Appl Math Comput,2011,217(22):9492-9496.
[23]El-Nabulsi A R,Torres D E M.Eractional actionlike variational problems[J].J Math Phys,2008,49:053521.
[24]El-Nabulsi A R.Universal fractional Euler-Lagrange equation from a generalized fractional derivate operator[J].Cent Eur J Phys,2011,9(1):250-256.
[25]Herzallah M A E,Muslih S I,Baleanu D,et al. Hamilton-Jacobi and fractional like action with time scaling[J].Nonlinear Dyn,2011,66(4):549-555.
[26]Zhang Y,Zhou Y.Symmetries and conserved quantities for fractional action-like Pfaffian variational problems[J].Nonlinear Dyn,2013,73(1/2):783-793.
[27]Zhang Y,Ding J E.Noether symmetries of generalized Birkhoff systems based on El-Nabulsi's fractional model[J].J Nanjing University of Science and Technology,2014,38(3):409-413.(in Chinese)
[28]Burgers J M.Die adiabatischen invarianten bedingt periodischer systems[J].Ann Phys,1917,357(2):195-202.
[29]Zhang Y,Ean C X.Perturbation of symmetries and Hojman adiabatic invariants for mechanical systems with unilateral holonomic constraints[J].Commun Theor Phys,2007,47(4):607-610.
[30]Jiang W A,Luo S K.A new type of non-Noether exact invariants and adiabatic invariants of generalized Hamiltonian systems[J].Nonlinear Dyn,2012,67(1):475-482.
[31]Jiang W A,Li L,Li Z J,et al.Lie symmetrical per-turbation and a new type of non-Noether adiabatic invariants for disturbed generalized Birkhoffian systems[J].Nonlinear Dyn,2012,67(2):1075-1081.
[32]Zhang Y.Perturbation to Noether symmetries and adiabatic invariants for generalized Birkhoffian systems[J].Bulletin of Science and Technology,2010,26(4):477-481.
[33]Chen J,Zhang Y.Perturbation to Noether symmetries and adiabatic invariants for Birkhoffian systems based on El-Nabulsi dynamical models [J].Acta Phys Sin,2014,63(10):104501-104507.
[34]Zhang Y.Method of Jacobi last multiplier for solving dynamics equations integration of generalized classical mechanics system[J].Journal of Nanjing University of Aeronautics and Astronautics,2012,44(2):262-265.(in Chinese)
(Executive editor:Zhang Tong)
O316 Document code:A Article ID:1005-1120(2015)04-0421-07
*Corresponding author:Zhang Yi,Professor,E-mail:zhy@mail.usts.edu.cn.
How to cite this article:Song Chuanjing,Zhang Yi.Perturbation to Noether symmetries and adiabatic invariants for generalized Birkhoff systems based on El-Nabulsi dynamical model[J].Trans.Nanjing U.Aero.Astro.,2015,32(4):421-427.
http://dx.doi.org/10.16356/j.1005-1120.2015.04.421
(Received 23 August 2014;revised 25 November 2014;accepted 10 December 2014)
 Transactions of Nanjing University of Aeronautics and Astronautics2015年4期
Transactions of Nanjing University of Aeronautics and Astronautics2015年4期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Optimization Method for Departure Flight Scheduling Problem Based on Genetic Algorithm
- Dynamic Surface Control with Nonlinear Disturbance Observer for Uncertain Flight Dynamic System
- Control of Vehicle Active Front Steering Based on Active Disturbance Rejection Feedback Controller
- Experiments on an Open-Loop Cycle Carbon Dioxide Refrigeration System
- Resolution Increase and Noise Removal in Particle Size Distribution Measurement with Shifrin Transform
- A Hydrodynamic Model for Dimpled Mechanical Gas Seal Considering Interaction Effect
