MULTIPLICITY RESULTS FOR FOURTH ORDER ELLIPTIC EQUATIONS OF KIRCHHOFF-TYPE?

Liping XU（許麗萍）

Department of Mathematics and Statistics，Henan University of Science and Technology，Luoyang 471003，China

Haibo CHEN（陳海波）?

School of Mathematics and Statistics，Central South University，Changsha 410075，China

MULTIPLICITY RESULTS FOR FOURTH ORDER ELLIPTIC EQUATIONS OF KIRCHHOFF-TYPE?

Liping XU（許麗萍）

Department of Mathematics and Statistics，Henan University of Science and Technology，Luoyang 471003，China

E-mail：x.liping@126.com

Haibo CHEN（陳海波）?

School of Mathematics and Statistics，Central South University，Changsha 410075，China

E-mail：math chb@csu.edu.cn

In this paper，we concern with the following fourth order elliptic equations of Kirchhoff type

fourth order elliptic equations of Kirchhoff type；symmetric mountain pass theorem；variational methods

2010 MR Subject Classification 35J20；35J65；35J60

1 Introduction

Consider the following fourth order elliptic equations of Kirchhoff type

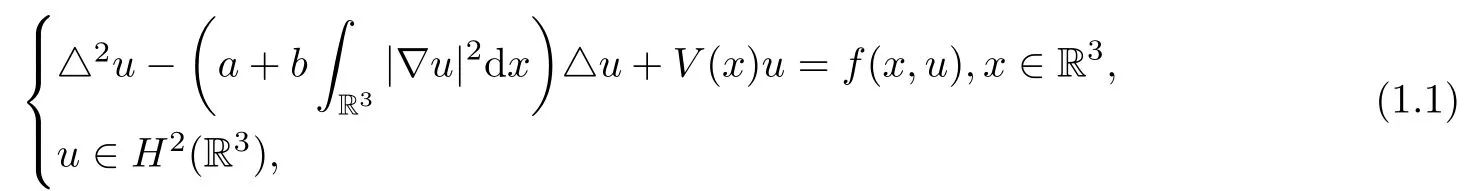
where a，b are positive constants.We assume that the functions V（x），f（x，u）and F（x，u）=（x，s）ds satisfy the following hypotheses.satisfieswhere a1＞0 is a constant.Moreover， for any M＞0，meas，where meas（.）denotes the Lebesgue measure in R3.

（f1）f（x，u）∈C（R3×R，R）and there exist α，β＞0 such that

（f4）There existμ＞4 and ρ＞0 such that

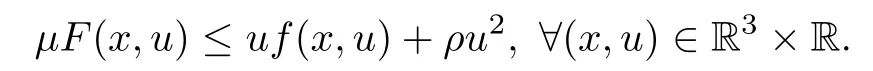
（f5）f（x，-u）=-f（x，u），?（x，u）∈R3×R.

（f6）There existμ＞4 and γ1＞0 such that

Problem（1.1）is a nonlocal problem because of the appearance of the termR3|?u|2dx which provokes some mathematical difficulties.This makes the study of（1.1）particularly interesting.Let V（x）=0，replace R3by a bounded smooth domain ??RNand set u=△u=0 on??，then problem（1.1）is reduced the following fourth order elliptic equations of Kirchhoff type

which is related to the following stationary analogue of the equation of Kirchhoff type

where△2is the biharmonic operator.In one and two dimensions，（1.3）is used to describe some phenomena appeared in different physical，engineering and other sciences because it is regarded as a good approximation for describing nonlinear vibrations of beams or plates（see［1，2］）.In［3］，Ma et al.considered existence and multiplicity of positive solutions for the fourth order equation

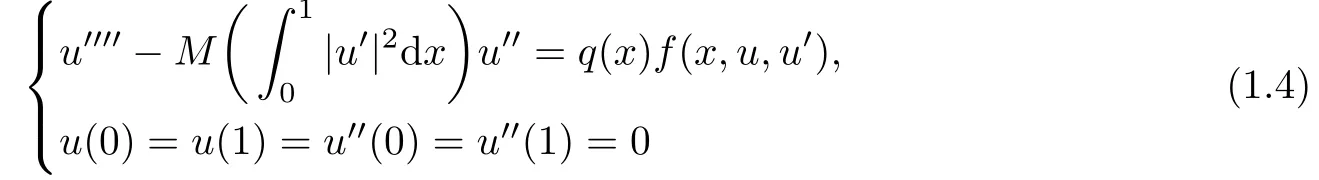
by using the fixed point theorems in cones of ordered Banach spaces.Recently，by the variational methods，Ma and Wang etc.studied（1.4）and the following fourth order equation of Kirchhoff type

and obtained the existence and multiplicity of solutions，see［4-6］.Very recently，Wang et al. considered the existence of nontrivial solutions for（1.2）with one parameter λ in［7］by usingthe mountain pass techniques and the truncation method.Chen and Xu［8］obtained infinitely many negative nontrivial solutions for（1.1）by genus theory.The solvability of（1.1）without△2andhas also been well studied by various authors（see［9］and the references therein）.

Motivated by the above works described，the object of this paper is to study the existence and multiplicity of solutions for（1.1）.Our main results are the following

Theorem 1.1 Assume that（V），（f1）-（f3）and（f5）hold，then problem（1.1）possesses infinitely many nontrivial solutions.

Theorem 1.2 Assume that（V），（f1）-（f2）and（f4）-（f5）hold，then problem（1.1）possesses infinitely many nontrivial solutions.

Obviously，we see that（f1）and（f6）imply（f4）.Then we have the following corollary.

Corollary 1.3 Assume that（V），（f1）-（f2）and（f5）-（f6）hold，then problem（1.1）possesses infinitely many nontrivial solutions.

Remark 1.4 Assume that（V），（f1）-（f2）and（f5）-（f6）hold，then problem（1.1）possesses infinitely many nontrivial solutions.

In our results，F（x，u）is allowed to be sign-changing.Obviously，the following nonlinearities f satisfy（f2）and（f3）or（f6）:

The outline of the paper is given as follows:in Section 2，we present some preliminary results.In Section 3，we give the proofs of Theorems 1.1，1.2.

2 Preliminaries

Let

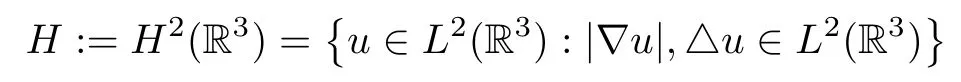
with the inner product and the norm

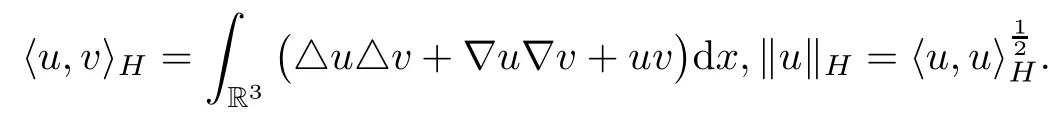
Define our working space

with the inner product and norm

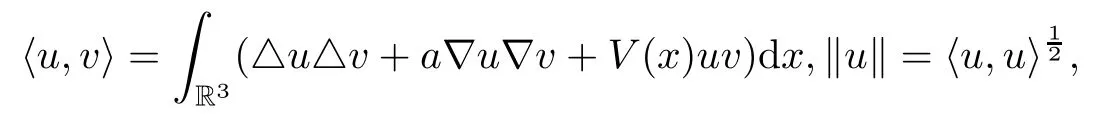
where‖·‖is an equivalent to the norm‖·‖H.Since the embedding E→Ls（R3）（2≤s＜6）is continuous，then there exists ηs＞0 such thatFurthermore，according to Lemma 3.4 in［11］，we can prove that under condition（V），the embedding E→Ls（R3）（2≤s＜6）is compact.Here we omit the proof for simplicity.We define the functional

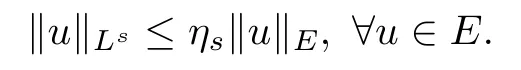
Lemma 2.1 Under conditions（V）and（f1），then I is of class C1（E，R）andfor all u，v∈E.

Proof For 0＜|t|＜1，u，v∈E，by（f1），mean value theorem and the H¨older inequality，we have

Then，by the Lebesgue dominated convergence theorem，we have

This implies（2.2）holds.

Set?E=｛u∈L2（R3）:?u∈L2（R3）｝with the norm‖u‖2?E=RR3|?u|2dx.Then the embedding E→ ?E is continuous.Let un→u in E，by the embedding theorem，un→u in Ls（R3）for any s∈［2，6）.First，we show that

In fact，then，by the H¨older inequality and Theorem A.4 in［12］，（2.6）implies（2.5）holds.Second，by the continuity of the imbedding E→ ?E and the boundedness of｛un｝，one has

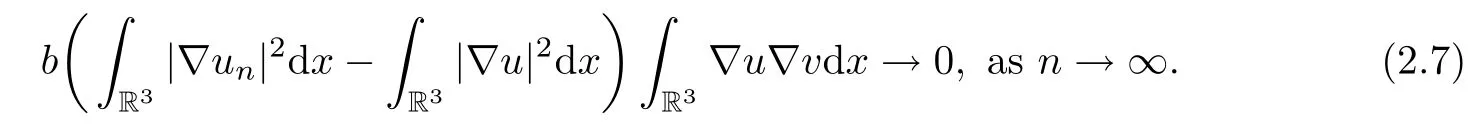
From（2.2），（2.5）and（2.7），one hasas n→∞，which implies the continuity of I′.The proof is completed.

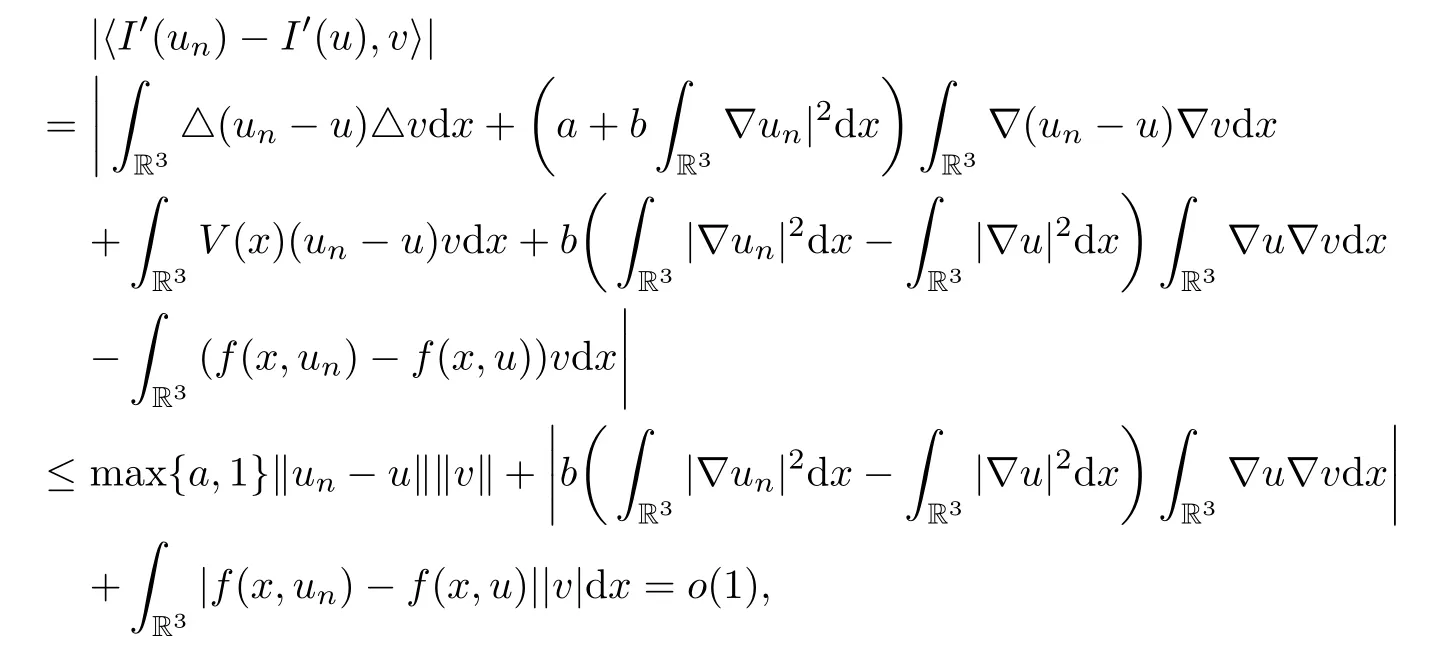
We say that I satisfies the Cerami condition（C）c，i.e.，any sequence｛un｝has a convergent subsequence in X whenever I（un）→ c and（1+‖un‖）‖I′（un）‖→ 0，as n→ ∞.In order to deduce our results，the following symmetric mountain pass theorem of Rabinowitz（see［13，Theorem 9.12］）is a very useful tool. □

Lemma 2.2（Symmetric Mountain Pass Theorem）Let X be an infinite dimensional Banach space and I∈C1（X，R）be even，satisfy the Cerami condition（C）cfor all c＞ 0. X=Y⊕Z，where Y is finite-dimensional.If I satisfies

（i）I（0）=0，

（ii）there exist constants ?，σ＞0 such that

（iii）for each finite dimensional subspace，there exists）such that I（u）≤0 onThen I possesses an unbounded sequence of critical values.

3 Proof of the Main Results

According to Lemma 2.2，we need the following lemmas.

Lemma 3.1 Assume V and（f1）-（f3）hold，then any sequence｛un｝satisfyingis bounded in E.

Proof If｛un｝is unbounded in E，we can assume‖un‖→+∞.For n large enough，by（2.1），（2.2）and（3.1），we have

By（2.1）and（3.1），we have

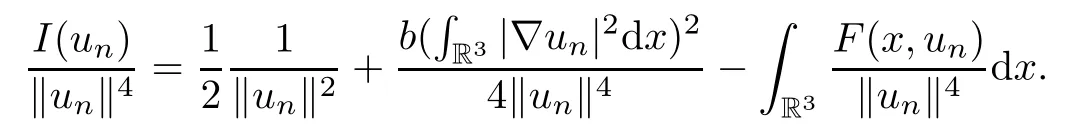
Then，

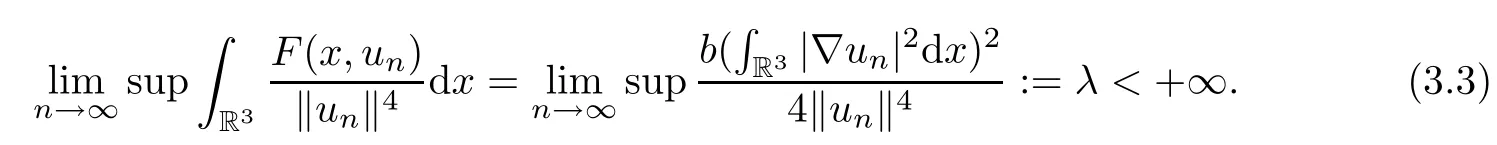
For 0≤a＜b，set

First，we consider the case v=0.If this is the case，then vn→0 in Ls（R3）（2≤s＜6），vn→0 a.e.on R3.It follows from（f1）that，

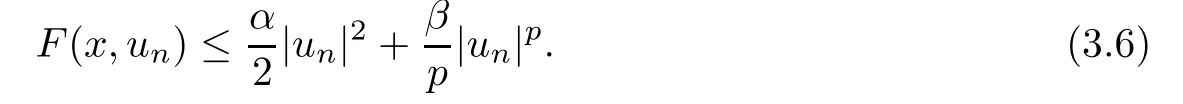
Then

as n→+∞.Consequently，Combining（3.7）with（3.8），one has

which is a contradiction to（3.3）.

For the second case v/=0，the set ?:=｛x∈R3:v（x）/=0｝has a positive Lebesgue measure.Then|un|→+∞for a.e.x∈?.Hence ???n（r0，∞）for large n.By（f2），（2.1），（3.2）and Fadou's lemma that

which is a contradiction.Thus｛un｝is bounded in E. □

Lemma 3.2 Assume（V）and（f1）-（f3），then any sequence｛un｝defined by（3.1）has a convergent subsequence in E.

Proof By Lemma 3.1，｛un｝is bounded in E.Going if necessary to a subsequence，we may assume that

Then，it follows from（f1），the boundedness of｛un｝and the H¨older inequality that

Z

By（2.2），we get

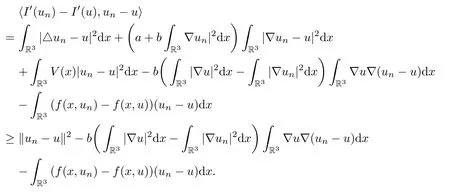
One has

It follows from（2.7），（3.1）and（3.11）that‖un-u‖→0.This completes the proof.

Lemma 3.3 Assume（V）and（f1）-（f3），then any sequence｛un｝defined by（3.1）has a convergent subsequence in E.

Proof By Lemma 3.1，｛un｝is bounded in E.Going if necessary to a subsequence，we may assume that

Then，it follows from（f1），the boundedness of｛un｝and the H¨older inequality that

By（2.2），we get

One has

It follows from（2.7），（3.1）and（3.11）that‖un-u‖→0.This completes the proof.

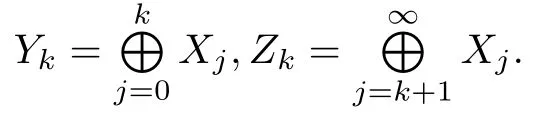
Lemma 3.4 Under assumptions（V）and（f1），there exist constants ?，σ＞0 such that I|?B?

∩Z≥σ.

Proof Set

Since E is compactly embedded into Ls（R3）for 2≤s＜6，there holds（see［14，Lemma 3.8］）

By（2.1）and（3.2），

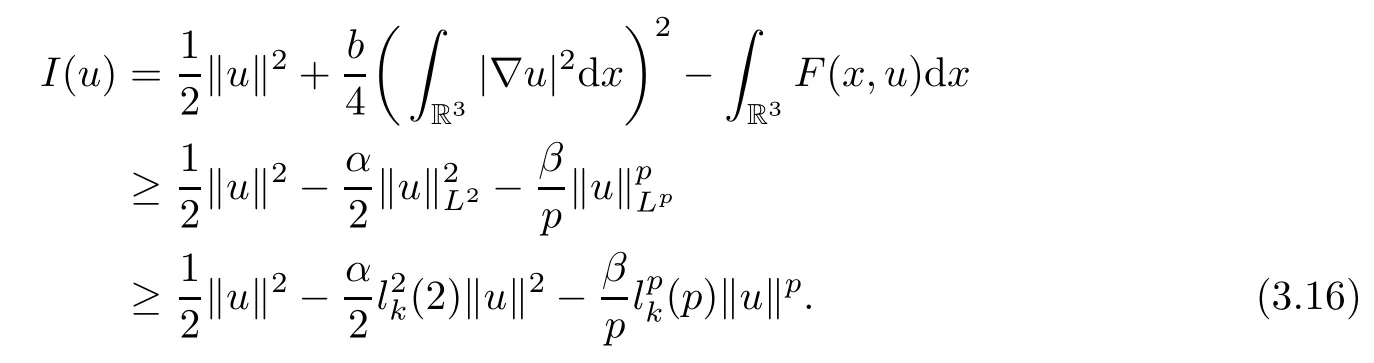
By（3.15），there exists a positive integer m≥1 such that

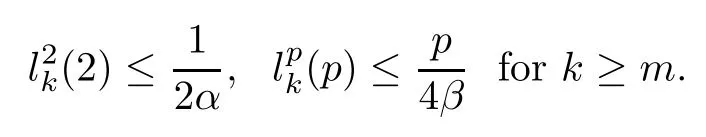
Then

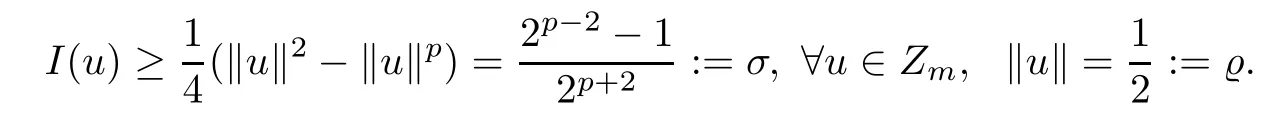
The proof is completed.

Lemma 3.5 Assume（V），（f1）and（f2），then for each finite dimensional subspacethere exists）such that

Then，by（2.1），（3.17）and（3.18），one has

for each u∈Em.Consequently，there is a large R＞0 such that I（u）＜0 onThe proof is completed.

Proof of Theorem 1.1 Obviously，I（0）=0 and I∈C1（X，R）is even.Then by Lemma 3.1，Lemma 3.2，Lemma 3.4 and Lemma 3.5，all conditions of Lemma 2.2 are satisfied.Thus， problem（1.1）possesses infinitely many nontrivial solutions.

Proof of Theorem 1.2 First，it easy to see I（0）=0 and I∈C1（X，R）is even.Then by Lemma 3.3，Lemma 3.4 and Lemma 3.5，all conditions of Lemma 2.2 are satisfied.Thus， problem（1.1）possesses infinitely many nontrivial solutions.

［1］Ball J M.Initial-boundary value for an extensible beam.J Math Anal Appl，1973，42:61-90

［2］Berger H M.A new approach to the analysis of large deflections of plates.J Appl Mech，1955，22:465-472

［3］Ma T F.Positive solutions for a nonlocal fourth order equation of Kirchhoff type.Discrete Contin Dyn Syst，2007，（Supplement）:694-703

［4］Ma T F.Existence results for a model of nonlinear beam on elastic bearings.Appl Math Lett，2000，13: 11-15

［5］Ma T F.Existence results and numerical solutions for a beam equation with nonlinear boundary conditions. Appl Numer Math，2003，47:189-196

［6］Wang F l，An Y K.Existence and multiplicity of solutions for a fourth-order elliptic equation.Bound Value Probl，2012:6

［7］Wang F l，Avci M，An Y K.Existence of solutions for fourth order elliptic equations of Kirchhoff type.J Math Anal Appl，2014，409:140-146

［8］Xu L P，Chen H B.Existence and multiplicity of solutions for fourth-order elliptic equations of Kirchhoff type via genus theory.Boundary Value Problems 2014，2014:212

［9］Wu Y Z，Huang Y S，Liu Z.Sign-changing solutions for Schr¨odunger equations with vanishing and signchanging potentials.Acta Mathematica Scientia，2014，34B（3）:691-702

［10］Kang D S，Luo J，Shi X L.Solutions to elliptic systems involving doubly critical nonlinearities and Hardtype potentials.Acta Mathematica Scientia，2015，35B（2）:423-438

［11］Zou W M，Schechter M.Critical Point Theory and its Applications.New York:Springer，2006

［12］Willem M.Minimax Theorem.Boston，MA:Birkh¨auser Boston Inc，1996

［13］Rabinowitz P H.Minimax Methods in Critical Point Theory with Application to Differential Equations. CBMS Reg Conf Ser Math，Vol 65.Providence，RI:American Mathematical Society，1986

［14］Zou W M.Variant fountain theorems and their applications.Manuscripta Math，2001，104:343-358

?Received January 17，2014；revised May 7，2015.This work was supported by Natural Science Foundation of China（11271372）and Hunan Provincial Natural Science Foundation of China（12JJ2004）.

?Corresponding author:Haibo CHEN.

where a，b＞0 are constants and the primitive of the nonlinearity f is of superlinear growth near infinity in u and is also allowed to be sign-changing.By using variational methods，we establish the existence and multiplicity of solutions.Our conditions weaken the Ambrosetti-Rabinowitz type condition.