高空核電磁脈沖晚期效應對電網穩定性影響的研究

趙志斌 柯俊吉 馬麗斌

（華北電力大學新能源電力系統國家重點實驗室，北京 102206）

高空核爆電磁脈沖（HEMP）的晚期效應即E3效應（簡稱HEMP E3效應），這種由高空核爆炸引起的低頻（約0.017Hz以下）、低幅值（約為數十伏/km）的電磁脈沖[1]會在交流輸電系統中產生低頻的準直流，從而導致系統中變壓器發生直流偏磁現象、中性點過流保護跳閘、繼電器誤動等后果，最終影響電力系統的正常運行。

20世紀 80年代開始了對于這一問題的研究，目前理論分析較少，研究主要依靠實驗的方式展開。國外學者作了大量研究工作，提出了不少的分析和計算方法，也做了相關驗證性的實驗。如 Rackliffe提出根據通過計算太陽風暴的地磁感應電流的方法，計算MHD-EMP的感應電流，最后對準直流電源系統中的感應電流進行了計算[2]；之后Meliopoulos用實際算例對 Rackliffe的闡述進行證明，并在473英里長線路系統上進行了兩者的比較與分析[3]。在模型計算方面，Lehtinen等將直流偏磁電源串聯到傳輸線網絡模型中[4-5]，然而 Albertson等人則將直流偏磁電源串聯接到變壓器中性線的接地點之上[6]。總而言之，各個計算方法不同之處在于直流激勵的引入方式不同。

國內學者對HEMP晚期效應的研究：Jin Liu等人采用了傳輸線模型[7-8]計算了核電磁脈沖對電力系統的效應和HEMP作用下傳輸線的感應電流計算[9-10]。然而，目前國內文獻都未曾考慮HEMP晚期效應對電力系統穩定性的影響。

基于國內外學者的研究成果，本文主要作如下研究：首先建立了地磁感應電流的電網模型，將地磁感應電流的計算問題轉化成電路問題，并采用Lehtinen與Pirjola的方法求解；然后以某750kV電網為實際案例計算地磁感應電流水平從而驗證模型與算法在此計算條件下的可行性；最后從斷路器、自耦變壓器等方面分別考慮高空核電磁脈沖晚期效應對電力系統的影響。

1 高空核電磁脈沖晚期效應產生地磁電流模型

1.1 計算模型

由于計算 HEMP E3效應感應電流的過程即為HEMP E3效應感應電場通過接地點作用于電網產生電流，所以可以將電場的作用等效為網絡中的電壓源，將HEMP E3效應感應電流的計算轉化為電路問題，從而通過等效的電網模型計算電網的 HEMP E3效應感應電流水平。

將變電站中的變壓器和電抗器等元件連接并等效得到變電站的等效模型。若變電站內有兩臺及以上變壓器并列運行，等效時應把相應元件的電阻并聯。變電站的接地電阻也包括感應電流等效模型，用Rd表示，其流過的感應電流為三相的總和，單相模型中的等效接地電阻應為實際三相的 3倍。即3Rd。

圖1 變電站等效電路圖

1.2 高空核電磁脈沖晚期效應的特性

高空核電磁脈沖晚期效應簡稱HEMP E3，文獻[5]指出若核爆炸的海拔高度介于 130～500km 之間，那么HEMP E3的影響區域達最大值。HEMP E3的時域波形采用了IEC 1000-7中給出的雙指數函數波形。其中HEMP E3出現于1～1000s之間，感應電場為水平方向。HEMP E3電場波形如圖所示，其峰值為 38V/km，上升時間約 0.9s，正脈沖半寬度20s，負脈沖半寬度130s。

圖2 HEMP E3的標準波形圖

1.3 計算方法

在電網模型中地面感應電場的作用等效為施加于接地點兩點間的電壓源，其值是電場的沿線積分，即

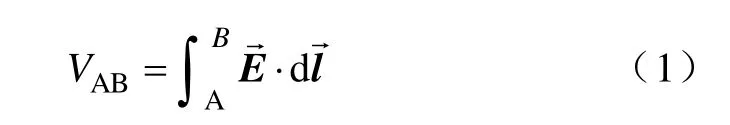
計算時，把整條線路→分成N段，線路的某一小段[i,j]內近似成直線，看成是均勻的，所以此段線路對應的等效電壓源如下式所示：

式中，Lij是線段長度，Ex、Ey分別是本段內與地面電場平行和垂直的北、東向分量，θ 為線段和y軸（東）之間的夾角，因此對應整條線路的等效電壓源即為各線段電壓之和。

經上述方法等效之后，則可以得到一只包含電阻和電壓源的電路網絡，其中網絡的節點即為變電站，每個節點和地間的電阻則是變電站接地支路的等效電阻，不同的節點和節點間的電阻是不同變電站之間輸電線路的等效電阻，節點與節點之間的電壓源是 HEMP E3電場在不同變電站接地點間的等效電壓源。

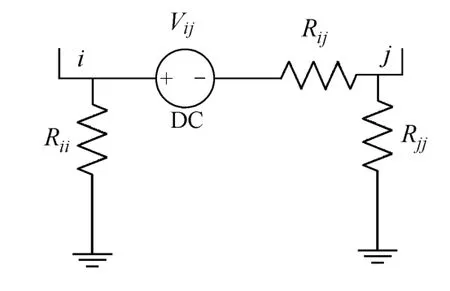
圖3 電網任意兩節點等效模型圖

當電網節點較多時，若使用回路電流法或節點電壓法，以形成電路的矩陣方程，此方法比較繁瑣，運算速度較為緩慢，為了提高計算的運行速度且便于編程，應用Lehtinen與Pirjola的方法求解。對于一個N節點的電網模型，其中任意兩點i和j間的等效電阻是Rij，接地支路的等效電阻為Z，兩點間的等效電壓源Vij，各條輸電線路上流過的感應電流Iij可由Lehtinen與Pirjola的方法計算得到：

2 高空核電磁脈沖晚期效應對系統穩定性的影響

為了提高電力系統運行的可靠性，首要任務是應加強系統抵抗干擾能力和完善系統結構。因此十分有必要對 HEMP E3效應作用下電網的感應電流水平進行研究，并以此來判斷其對電網的威脅。

2.1 HEMP E3效應作用下的感應電流水平

本文以電壓等級較高、覆蓋面積大的某 750kV電網為例分析了 HEMP E3效應在電網中產生的感應電流，由于沒有公開資料給出E3電場的空間分布特性，所以在計算時，未考慮高空核爆炸電磁脈沖E3效應在不同空間位置的變化。

某750kV電網如圖4所示。本文計算了均勻分布的HEMP E3電場下（即方向和大小d不隨位置改變而變化）。

圖4 某750kV電網示意圖

圖5給出了最大情況下流過各變電站每臺變壓器的感應電流。可以看出，在格爾木變電站的感應電流水平最高，可達 4000A。考慮到在變壓器中性點串聯小電阻，可以有效降低感應電流，圖5給出了不同電阻值情況下的計算結果。從圖中可以看出，即使采用 10Ω的電阻，部分變壓器地磁感應電流的最大值仍超過1000A。

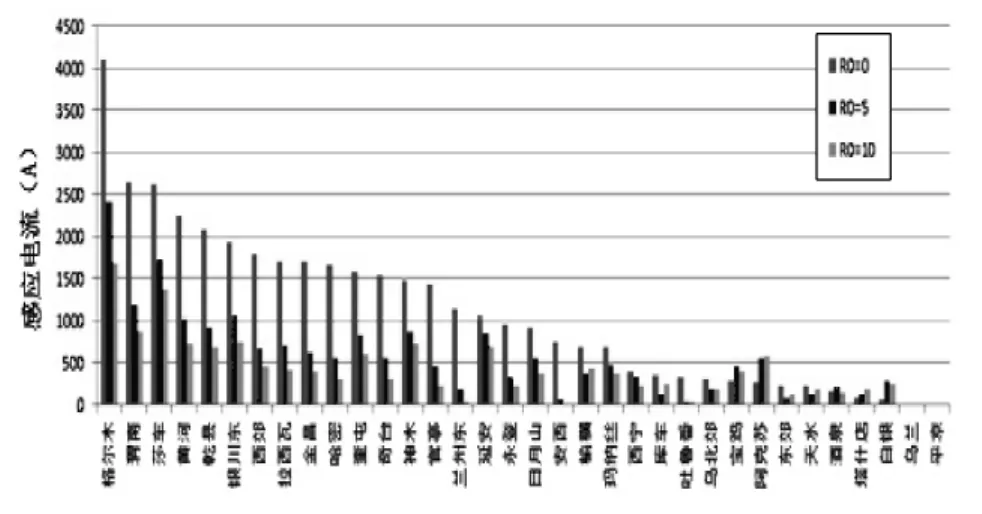
圖5 750kV各變電站在HEMP E3作用下的感應電流

由電磁感應定律可知:時變的磁場在大地中感應出電場，此地電場又會在接地的導體網絡中產生地磁感應電流，稱此感應電流為 SS-GIC（Solar storm-geomagnetically induced current）。同理 HEMP E3效應所感應出的電流被稱為 MHD-GIC（magnetohydrodynamic-geomagnetically induced current）。二者頻率都極低，近似于直流。從文獻[11]中監測數據上看，太陽磁暴所導致的 SS-GIC峰值一般在50A左右，所以高空核爆炸電磁脈沖晚期效應造成的瞬時影響比太陽磁暴的影響要大得多。

據文獻[12]所給出的太陽磁暴地面電場計算結果其場強峰值不超過 1V/km，SS-GIC最大不超過150A。本文所計算的MHD-GIC都以HEMP E3峰值38V/km計算，最大達到4000A。二者對比結果可以驗證模型與算法在此計算條件下的可行性。

2.2 高空核電磁脈沖晚期效應感應電流對系統中斷路器的影響

在斷路器的開發過程中很大程度上依賴于電流中斷裝置的設計，而電流中斷裝置遵循交流電流的特性，自然電流為零時才允許電流中斷。開斷幅值較大的直流只能依據一般的理論認識，HVDC傳輸線的開關則需人工方法，在所需的直流電流中斷的時間內產生一個電流零點。

如前所述，HEMP E3效應會給電網帶來較大的感應電流。如圖6所示，750kV傳輸線上HEMP E3影響下的交流電流在2s左右達到高峰，然后慢慢衰減。值得注意的是，疊加的交流和直流電流峰值時是正常交流電流的兩倍左右，而且會阻礙正常的交流電流過零時間（20s左右）。

圖6 某750kV傳輸線正常情況下的交流電流和HEMP E3效應下的交流電流

2.3 高空核電磁脈沖晚期效應感應電流對電力變壓器的影響

HEMP E3效應感應電流影響下的電力變壓器呈現一種非正常工作狀態，變壓器中流過較大偏磁電流，鐵心將出現磁飽和現象，導致變壓器鐵心中含有直流磁通，此時鐵心比正常工作時產生大考慮磁滯效應時。當存在感應電流的時候，勵磁電流的波形發生了嚴重畸變，正半波出現尖頂，且其峰值相較于不存在感應電流時大了很多。變壓器勵磁電流峰值的增加，會導致變壓器無功消耗增加、變壓器的漏磁增加、鐵心高度飽和、勵磁電流畸變、變壓器器身振動、油箱油溫上升或金屬構件局部過熱、以及變壓器壽命減短等不利后果。

3 結論

本文主要回顧 30余年來國內外學者對高空核電磁脈沖晚期效應的研究歷程，并基于前人的研究成果分析了高空核電磁脈沖晚期效應對實際高壓電網系統穩定性的影響，最終得出如下結論：

1）建立了變電站等效模型，并在此基礎上應用Lehtinen與Pirjola方法計算了HEMP E3效應作用下某750kV電網HEMP E3效應感應電流，從而驗證了模型與算法在此計算條件下的可行性。

2）本文對高空核電磁脈沖晚期效應對實際高壓電網的可能帶來的威脅進行分析，HEMP E3期間斷路器存在不能正常切斷故障電流可能性，HEMP E3所感應出的感應電流與工頻電流疊加，導致重合閘不成功。

[1] Kenneth W, Paul R. Electromagnetic pulse and the electric network[J]. IEEE Transactions on Apparatus and Systems, 1985, 104(6): 1571-1578.

[2] Kruse V J, Rackliffe G B, Barnes P R. Load flow studies in the presence of magnetohydrodynamic electromagnetic pulse[J]. IEEE Transactions on Power Delivery, 1990, 5(2): 1158-1164.

[3] V J Kruse, D L Nickle, J J Bonk, E R Taylor.Impact of a nominal nuclear electromagnetic pulse on electric power systems[R].Martin Marietta Energy Systems,Inc, 1991：1-2．

[4] Pirjola R, Viljanen A. On geomagnetically-induced currents in the Finnish 400 kV power system by an auroral electrojet current[J]. IEEE Trans.Power Delivery, 1989, 4(2): 1239-1245.

[5] Lehtinen M, Pirjola R. Currents produced in earthed conductor networks by geomagnetically-induced electric fields[J]. Annales Geophysicae, 1989, 3(4):479-484.

[6] Boteler D H, Bui V Q, Lemay J. Directional sensitivity to geomagnetically induced currents of the Hydro-Quebec 735 kV power system[J]. IEEE Trans. Power Delivery, 1994, 9(4): 1963-1971.

[7] 謝彥召, 王贊基, 王群書. 地面附近架高線纜HEMP響應計算的 Agrawal和 Taylor模型比較[J]. 強激光與粒子束, 2005, 17(4): 575-580.

[8] 張志軍. 電磁脈沖對傳輸線耦合規律的研究[D]. 北京: 華北電力大學, 2006.

[9] 黃聰順, 周啟明. 高空電磁脈沖作用下地面電纜屏蔽層感應電流的數值模擬[J]. 強激光與粒子束,2003, 15(9): 905-908.

[10] 敬文濤. 導彈線纜高空核爆電磁脈沖耦合效應的研究[A]. 國防科學技術大學研究生院論文, 2004.

[11] 中華人民共和國發展與改革委員會, DL/T 5224—2005. 高壓直流輸電大地返回運行系統設計技術規定[S]. 2005.

[12] 劉春明. 中低緯電網地磁感應電流及其評估方法研究[D]. 北京: 華北電力大學, 2009.