一種基于屬性測度的改進時域融合識別方法

陳光輝，宋小梅

(南京電子技術研究所， 南京210039)

0 引言

在日益復雜的戰場環境中，基于戰術使用的電子偵察系統對輻射源識別的速度和準確率提高了要求。由于輻射源識別仍然要面臨輻射源具有多種工作模式且不同輻射源工作模式相互交疊和輻射源庫不完整性、不確定性兩方面的問題，因此，這種戰術應用場合下的輻射源識別方法要具有相對識別速度快、識別準確以及能夠識別復雜輻射源信號的優點。

數據庫比對法應用與研究的時間最長，技術相對成熟，是目前偵察設備普遍使用的輻射源識別方法。其中幾種應用和研究較多的算法有:灰關聯法、模糊匹配法和屬性測度法等［1］。為提高單個傳感器識別的準確度，文獻［2］和文獻［3］分別提出了采用灰關聯法、模糊匹配法獲取基本概率賦值函數(BPAF)，在此基礎上應用D-S證據理論進行證據組合與決策實現目標識別。這些都為輻射源識別提供了很好的思路。

文獻［2］中通過計算關聯度來衡量兩數列的接近程度，關聯度間接取決于數列間的絕對差值的大小，因此，易受數值波動的影響，即抗噪聲性能不是很理想，由此獲取的BPAF會影響到后續的融合識別。文獻［3］中模糊匹配的取大取小運算損失了部分中間值的信息，使得識別不夠細微，難以識別復雜輻射源信號。因此，在實際的雷達輻射源識別設計中，有必要進一步提高識別效果和識別速度。

本文提出的采用屬性測度法獲取BPAF，并結合D-S證據理論對多量測周期識別結果進行融合的識別方法，在一定程度上解決了上述問題:采用樣本訓練方法，大量的計算在比對識別之前就已完成，識別速度很快;引入統計的思想獲取BPAF，使得融合識別受噪聲影響的程度降低，識別效果得到提高。

1 基于屬性測度模型的雷達輻射源識別算法

屬性測度、屬性模式識別理論在環境質量評價及生物、石油勘探、經濟中取得了成功的應用。本文將這種屬性測度的思想結合樣本訓練應用到對雷達輻射源的識別中。

1.1 單指標屬性測度計算

選取已知雷達數據庫中的輻射源數據為已知樣本數據，提取描述輻射源的特征指標。設已知樣本空間分成K類，第k類為Ck，1≤k≤K。每一個樣本有射頻、脈沖重復頻率、脈沖寬度、脈內調制類型等J個指標，第 j個指標記為 Ij，1≤j≤J，指標 Ij可以為定性指標也可以為定量指標，但Ij的級別或取值為有限個。設指標 Ij有 Lj個級別，第 l個級別為 Ijl，1≤l≤Lj。

已知屬于Ck類的樣本有Nk個:x(k)n，1≤n≤Nk，1≤k≤K。樣本x(k)n在指標Ijl上的值為x(k)n(jl)，jl)滿足［4］

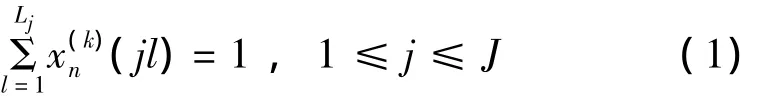
Ck的已知樣本在指標Ij上的分布

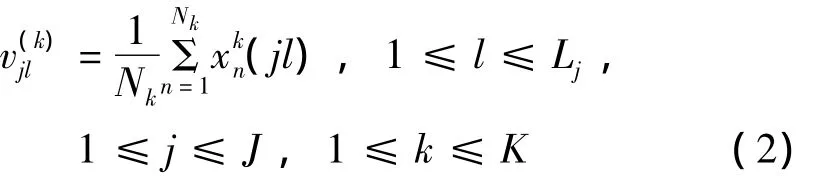
指標 Ijl在類分割(C1，C2，…，Ck)上的分布

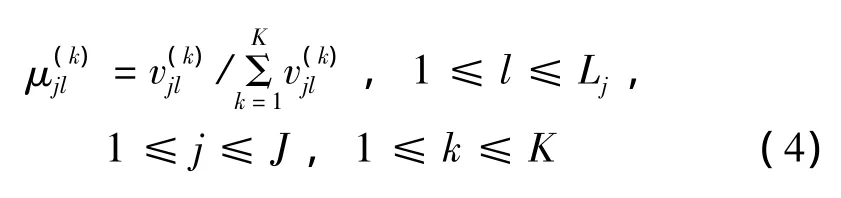
由以上計算可以看出，式(4)反映了各類中的指標在區間(指K類已知樣本的最大可能參數分布區間)內各級別的統計分布情況。

1.2 指標權重的計算

指標的重要性體現在已知樣品x的單指標屬性測度μ(k)ij和綜合屬性測度μ(k)i的近似程度上，越近似表明指標越能反映總體情況，權應越大［5］。具體算法為平均權算法，即ωj=1/J綜合屬性測度為

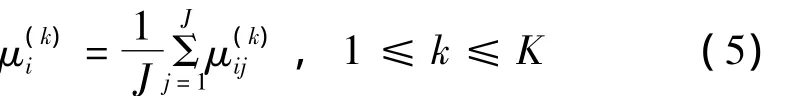
計算屬性相關系數

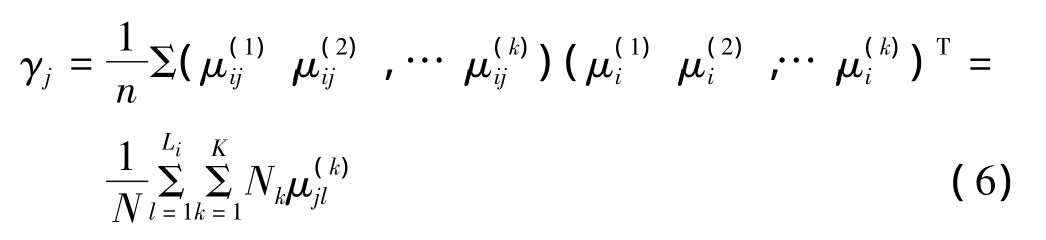
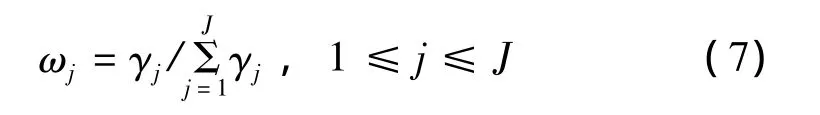
這種完全基于輻射源庫樣本訓練統計得出的指標權重，避免了主觀確定方法帶來的影響和干擾。從計算中可以發現，樣本指標的取值沿區間分布越均勻，即重疊越少，該指標權重越高。這與實際情況是符合的，重疊越少，誤識別的概率越小，該指標在決策中的重要性應該越高。

1.3 屬性測度的計算及屬性判別

設待識別樣本x在指標Ij上的值為xjl，則x屬于Ck的屬性測度

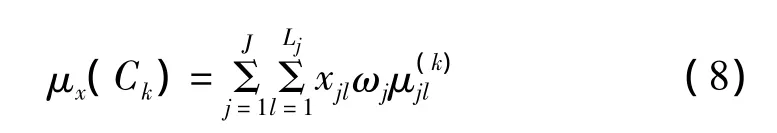
屬性測度μx(Ck)反映了待識樣本x歸屬于已知樣本空間中類Ck的程度的一種度量。式(8)通過統計待識樣本在類中各指標出現的概率，并進行指標加權來計算其歸屬于相應類的程度。

2 多量測周期的融合識別算法

一般的電子偵察系統可獲取輻射源多個量測周期的樣本，根據上述的屬性測度識別方法可實現基于單個量測周期的輻射源的識別。由于量測周期間輻射源工作模式可能變化以及受噪聲的影響，各周期獲取的樣本的特征參數值是變化的，每個量測周期的識別結果的可信度是波動的。為提高識別結果的可信度，必須要將各周期的識別結果進行數據融合［5-6］。

D-S證據理論采用信任函數而不是概率作為度量，不需要先驗概率和條件概率密度，可以處理由模糊引起的不確定性，是信息融合中的重要工具［7］。

2.1 算法的描述

基于屬性測度單量測周期的識別結果，應用D-S證據理論進行多量測周期的融合識別算法的基本步驟如下:

(1)屬性測度的計算

由式(1)～式(7)對輻射源庫中樣本訓練的結果獲取指標的權重ωj和分布μ(k)jl。然后，根據式(8)計算待識樣本x屬于Ck的屬性測度μx(Ck)。

(2)BPAF的獲取

設識別框架Θ包含有意義的識別命題有K個(A1，A2，…，AK)。第 i(i=1，2，…，P)個量測周期命題mi(Ak)，即待識目標x屬于輻射源庫中第k類Ck的基本概率賦值函數

設未知命題的基本概率賦值為0。

(3)證據組合

我們對腦電生物反饋治療方式的效果和安全性進行了研究,腦電生物反饋治療時物理治療,效果好,安全性高,對焦慮、抑郁等障礙有很好的治療效果。治療的時候,操作人員接收患者的腦電信號,通過及技術來進行處理,通過音樂和游戲等反饋到大腦,讓患者有意識的進行機體活動調整,改善自身的情緒狀態。

依據P個測量周期的累積量測，由Dempster組合規則可得到第k個命題的融合后驗BPAF

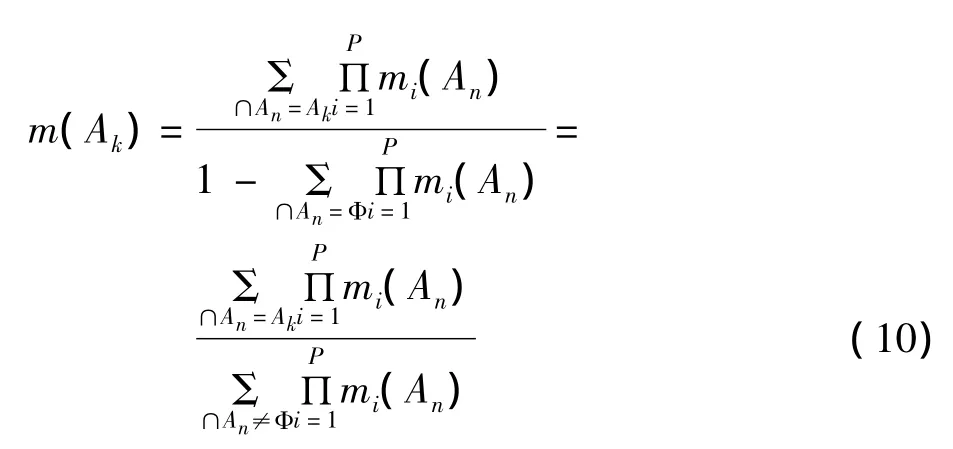
未知命題融合后驗BPAF為0。

(4)決策

用證據理論組合證據后基于BPAF進行決策，即輻射源所屬類別應具有最大的BPAF，輻射源類別的BPAF和其他類別的BPAF的差值必須大于某一閾值，不確定區間的程度小于某一閾值，且輻射源雷達的BPAF必須大于不確定區間的長度。具體描述如下:

設 A1，A2?Θ 滿足

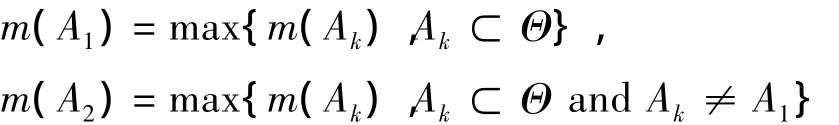
且有

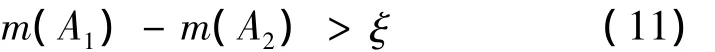
2.2 與其他方法的比較

為了說明本文方法(如圖1)具有識別速度快的特點，將其與文獻［2］和文獻［3］提出的輻射源識別方法(如圖2)進行了比較。如圖1，虛線框內表示算法中運算量較大的地方，顯然這一較大的運算在多個量測周期內被反復執行，降低了識別的速度。圖2中大量的運算(如圖2中虛線框內所示)是對輻射源庫中的樣本訓練，這是在識別之前就完成的。且一次樣本訓練適用于多個量測周期，因此，該法在進行多個周期的融合識別時，提高了識別的效果卻沒有相應增加較大的運算量。對于所提方法的識別準確度以及適應復雜信號的情況將在下面的仿真中做進一步分析。

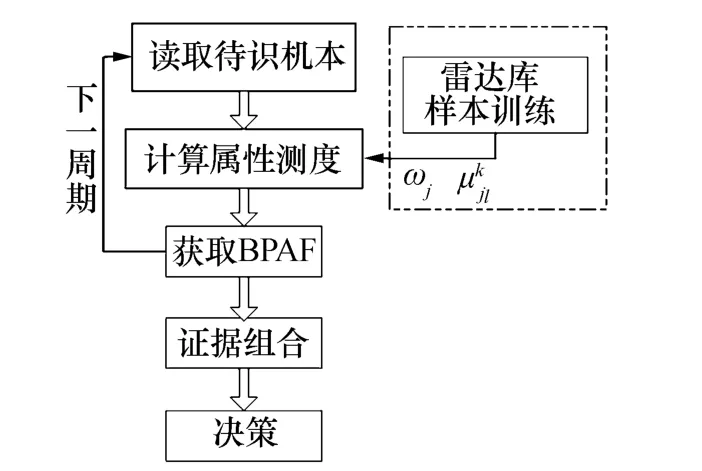
圖1 基于屬性測度的時域融合識別方法

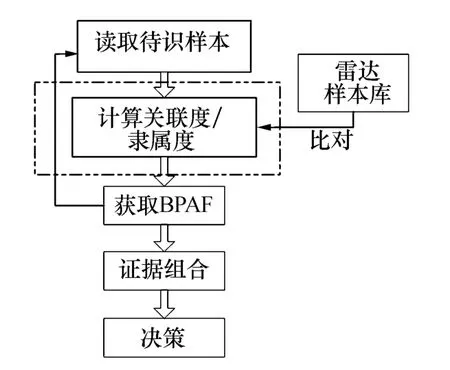
圖2 灰關聯法/模糊匹配法與證據理論結合的方法

3 模擬與仿真

為了驗證本文算法的性能，首先，建立雷達偵收頻段內的機載雷達數據庫，特征參數由載頻、重復頻率和脈沖寬度構成;然后，在實驗時用目標模擬器模擬雷達庫中的一種型號雷達的特定工作模式的信號，同時使該型雷達工作在電子偵察方式下對其偵收，獲取不同量測周期待識樣本的特征參數，分別改變目標模擬器模擬的雷達的工作模式獲取待識樣本做進一步識別;最后，改變目標模擬器輸出信號的信噪比，驗證在不同參數測量誤差條件下的識別效果。以下是對部分仿真和實驗的描述。

3.1 識別過程仿真

選擇目標識別框架為 Θ={A1，A2，A3}，其中，A1、A2、A3為已知雷達庫中的雷達型號。用目標模擬器依次模擬雷達庫不同型號雷達不同模式下的信號特征參數，同時，使該型雷達至少偵收到三個量測周期的待識樣本。

(1)將三個指標(特征參數)分別劃分10個小區間，每個區間對應的就是指標的一個級別。對每一個樣本，若待識樣本指標值落在某一個小區間上，則該指標值在相應的指標級別上取值為1，否則為0。指標區間的劃分不是固定的，要根據實際參數分布情況來定。

(2)通過對雷達庫中的樣本訓練，計算各量測周期的屬性測度，獲取的BPAF如表1。表示第i個量測周期確定的BPAF。

(3)基于所有周期的累積量測，利用D-S證據理論計算融合后的BPAF，如表2所示。

(4)選取ξ的值為0.3，決策結果為A1。

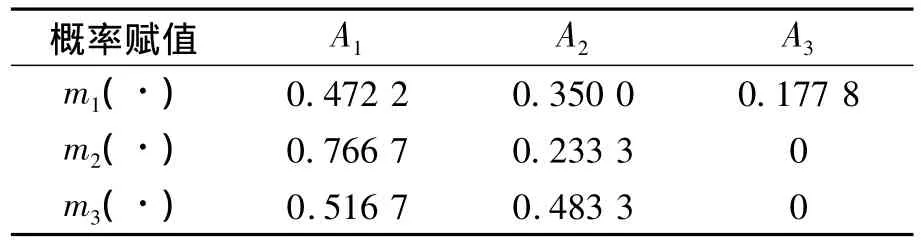
表1 各量測周期的BPAF

表2 融合后的BPAF

識別過程仿真表明:在一定的測量誤差范圍內，通過對各量測周期的識別結果進行有效的融合之后，識別效果得到很大程度地提高。

3.2 對比實驗

重復3.1節中的實驗方法，改變目標模擬器輸出信號的信噪比。在不同信噪比條件下獲取不同測量誤差的待識樣本參數值，分別采用本文方法和灰關聯法獲取BPAF的融合識別法進行對比實驗。其中，灰關聯法采用平均權計算關聯度。經過1 000次的Monte Carlo實驗，得到的實驗結果如表3所示。其中，σ代表已知雷達數據庫的標準偏差，誤差范圍分別控制在0.5、1.0、1.5 和2 倍標準差內。

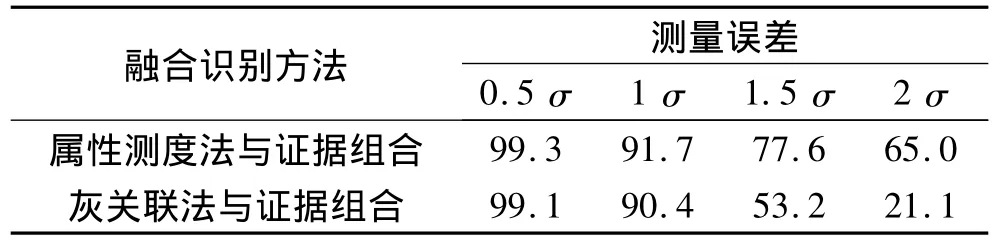
表3 不同條件下的正確識別率 %

由表中可以看出，灰關聯法獲取BPAF進行的融合識別受噪聲影響仍然很大。而本文方法由于引入了統計的思想獲取BPAF，因此，在適應噪聲干擾方面得到了較好的改善。需要說明的是，待識樣本選取特定類中不同的工作模式時，正確識別率會有區別。這與實際輻射源可能會出現工作模式交疊的情況相符，如選擇待識樣本為重頻抖動模式，正確識別率降低很多。

4 結束語

經過大量的識別和對比實驗表明，本文采用的基于屬性測度的改進時域融合識別方法是一種實時、有效的輻射源識別方法:(1)采用樣本訓練方法，大量的計算在比對識別之前就已完成，大大減少了識別時的計算量。因此，多個周期的融合識別在提高識別準確度的同時，只增加較小的運算量。(2)引入了證據理論進行時域融合，通過對信號的積累和對信任度的重新分配，對識別結果進行了有效的融合，提高了輻射源的正確識別率。(3)通過構造指標級別來區分信號參數間的細微差別，可以對頻率捷變、重頻及脈寬變化等復雜雷達信號進行樣本模式構造，從而完成復雜信號識別。

［1］陳昌孝，何明浩，徐 璟，等.雷達輻射源識別技術研究進展［J］.空軍預警學院學報，2014，28(1):1-5.Chen Changxiao，He Minghao，Xu Jing，et al.Progress of study on recognition technology of radar emitter［J］.Journal of Air Force Early Warning Academy，2014，28(1):1-5.

［2］李 楠，曲長文，蘇 峰，等.灰色關聯理論在輻射源識別中的應用［J］.系統仿真學報，2009，21(24):7896-7898.Li Nan，Qu Changwen，Su Feng，et al.Application of gray association theory in emitter recognition［J］.Journal of System Simulation，2009，21(24):7896-7898.

［3］張英鑫，王寶樹.模糊匹配方法及證據理論在輻射源識別中的應用［J］.計算機工程，2005，31(22):183-185.Zhang Yingxin，Wang Baoshu.Application of fuzzy matching method and evidence theory in field of recognition for radiant point［J］.Computer Engineering，2005，31(22):183-185.

［4］李 楠，曲長文，蘇 峰，等.基于屬性測度理論的輻射源識別［J］.現代防御技術，2010(4):93-96.Li Nan，Qu Changwen，Su Feng，et al.Emitter recognition based on the attribute measurement theory［J］.Modern Defence Technology，2010(4):93-96.

［5］Yager R R.Uncertainty representation using fuzzy measure［J］.IEEE Transactions on SMC，Part B，2002(30):13-20.

［6］Kawalec A，Owczarek R.Radar emitter recognition using intrapulse data［C］//Proceedings of 14th International Conference on Microwaves，Radar and Wireless Communications.Amsterdam:Academic Press，2004:249-252.

［7］孫即祥.現代模式識別［M］.長沙:國防科技大學出版社，2003.Sun Jixiang.Modern pattern recognition［M］.Changsha:National University of Defense Technology Press，2003.