基于典型樣本的信度函數分配的構造方法

王 霞，田 亮

（華北電力大學控制與計算工程學院，河北保定071003）

基于典型樣本的信度函數分配的構造方法

王 霞，田 亮

（華北電力大學控制與計算工程學院，河北保定071003）

D-S證據理論信度函數分配的取值是得到較為準確的融合結果的關鍵，然而傳統方法如采用隸屬度函數、正態分布等得到的信度函數分配都具有較大的主觀性。為使信度函數分配更具客觀性，在總結其它方法的基礎上，提出了基于典型樣本的信度函數分配構造方法。首先采集各目標模式下的樣本，并判斷每一模式下的各條證據服從何種概率分布，利用相應的概率公式計算待識別目標模式的各條證據的概率密度，然后進行歸一化處理，最后利用聯合規則得到融合結果。實例表明利用此法可得到較為準確的融合結果，不僅提高了判別結果的準確性，而且降低了不確定度，并再一次證明了融合診斷結果比單一數據具有更高的可靠性。

證據理論；信度函數；典型樣本；概率分布

0 引言

由于D-S證據理論數據融合算法比單一傳感器診斷結果可靠，故其在融合診斷和模式識別方面得到了廣泛應用［1］。在證據體確定的情況下，由于聯合規則是固定的，所以信度函數分配的獲取就造成了融合結果的不同。目前信度函數分配的獲取大致有以下幾種方法:把隸屬度函數經適當變換代替專家經驗得到基本概率，概念清晰，使用方便，但易受個人經驗的影響［2］；采用漢明距離得到信度函數分配，意義明確，較為簡單，但目標模式較多時，會產生信息丟失現象［3］；利用正態分布計算證據在各目標模式下的信度密度值，然后進行歸一化處理得到信度函數分配，意義明確，減小了對專家經驗的依賴，但有時候證據的概率密度并不服從正態分布［4，5］。

本文在總結以上文獻中經驗的基礎上，提出首先對大量歷史樣本進行分布判斷，然后選取相應的概率密度函數計算待判別目標模式的概率密度，然后進行歸一化處理得到信度函數分配值，這種方法物理意義明確，與實際的結果相吻合，有效減小了對專家經驗的依賴。

1 相關概念

1.1 識別框架

如果定義代表某一事物的參數為θ，可能取值的集合為Θ，則稱Θ為識別框架。在故障診斷中，每一種可能的故障都為假設，各種可能故障的集合為識別框架，故障的每一癥狀為證據。

如果Θ是一個識別框架，那么函數m:2Θ→［0，1］稱為基本概率分布，滿足:

式中:m（ui）表示證據分配到ui上的信度函數值，m（ui）越大，表明該條證據可信度越大；反之則說明該條證據的可信度越小。

1.2 聯合規則

根據D-S聯合規則，設m1，m2分別為同一識別框架Θ上的2個信度函數分配［6］，焦元分別為:｛u11、u21、…ui1｝，｛u12、u22、…uj2｝，設:

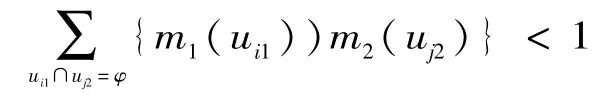
則由下式定義的函數:

當uk=Ф時，m（uk）=0，式中:i、j、k= 1、2、…n；其中:

為聯合后的信度函數分配。C是表示完全沖突假設ui1和uj2所有信度函數乘積之和，所謂完全沖突是指ui1和uj2在Θ中不可能同時發生。對于D-S證據理論，其結果不受證據組合次序先后的影響，但在證據較多時，可先將證據兩兩融合，盡量避免使用中間融合結果，提高計算的精度和準確率。

1.3 融合結果判定規則

盡管有很多不同的案例，但是對于目標模式的判定具有相似的基本規則:

（1）因為信度函數分配代表了可信度的大小，顯然信度函數分配值最大的目標模式可作為最終的判定結果。

（2）為了較少模棱兩可的情況出現，判定的目標模式和其它任一目標模式信度函數分配值之差應大于某個限值，此限值依具體情況而定。

（3）整個目標系統的不確定度必須小于某個限值［2］，以提高判別結果的可靠性。

2 信度函數分配的獲取方法

2.1 典型樣本

設待識別的目標模式為｛u1，u2，u3，…，un｝，對任一目標模式存在m個相互獨立的特征變量對其進行描述，設為｛x1j，x2j，x3j，…xmj｝，j∈m，即為待融合的目標模式。所有目標模式下的各證據的典型值為｛x′1j，x′2j，…，x′mj｝，稱為典型樣本。

在實際生產中，由于歷史數據較多，難以確定典型樣本，任一目標模式下的特征變量的取值可以是某一區間內的任一值。某一樣本出現的次數越多，其發生的概率越大，因此可以將概率密度值最大的樣本作為典型樣本。

2.2 概率密度函數

各目標模式下的特征變量是一個隨機變量，本文將探討的變壓器故障診斷的實例中，特征變量是一個非負實數，且取值具有一定的概率密度f（x）。f（x）與置信概率p之間存在如下關系:

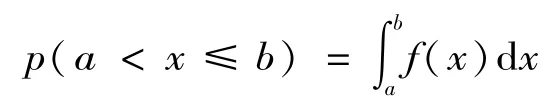
各目標模式下的證據分布可能相同或不同，至于服從何種分布可以利用MATLAB程序對樣本進行判斷。通常情況下，樣本量越大，對概率分布的判斷就越準確。整理文獻［7］附錄提供的數據并進行概率分布判斷，得出其均服從對數正態分布。而對數正態分布的概率密度函數f（x）為

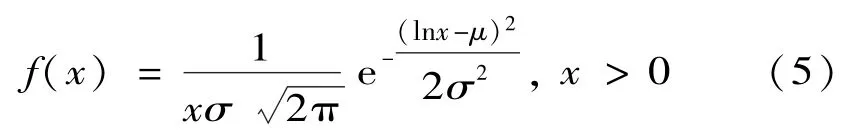
對數分布的概率密度y與隨機變量x的函數圖像如圖1所示。

圖1 對數分布的概率密度函數

圖1（a）所示的是μ相同而σ不同時對數分布的概率密度函數的圖形。

圖1（b）是σ相同而μ不同時對數分布的概率密度函數的圖形。

由對數分布的概率密度函數公式和圖形可以得出以下結論；

（1）f（x）取最大值時的x值為

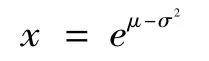
而此時的概率密度值為:

（2）μ相同時，σ越小，f（x）的極大值點越大；σ相同時，μ越大，f（x）的極大值點越大。

圖2是置信概率p與x之間的關系。

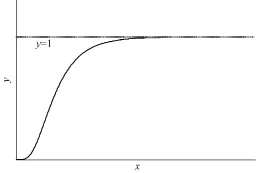
圖2 對數分布的累加函數

因此可將f（xij）定義為證據xi在模式uj下的信度密度函數。而對數分布置信區間的構造可采用P值方法［8］，置信度為1-α的置信區間為:

具體計算方法為:

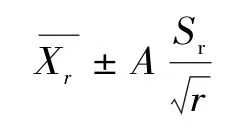
式中:第一項是樣本的均值；Sr是樣本的標準差；r是樣本個數；A可根據α和r的大小查T分布表得到。

從圖1可以看出μ越小，概率密度越集中；σ越大，概率密度的極大值點越小，說明引入置信區間的必要性。

在置信區間改變后，概率密度函數的定義域也隨之改變，此時的概率密度分布函數記為M（xij），并將其定義為證據xi在目標模式uj下的信度密度函數。

2.3 信度函數分配的構造

引入信度密度函數的目的就是構造信度函數分配。任一條證據xi對應n個信度密度函數值，記為:｛M（xi1），M（xi2），…，M（xin）｝，將不確定的信度密度值定義為n個信度密度函數的標準差［9］，即:

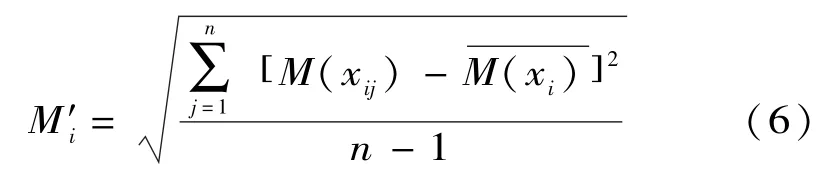
其中:

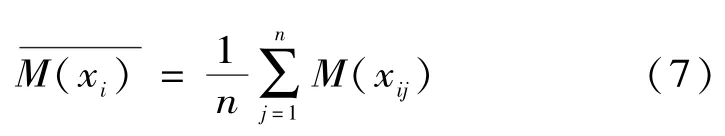
對各信度密度值進行歸一化處理，n+1個信度密度值之和為:

定義證據xi在目標模式uj下的信度函數分配為:

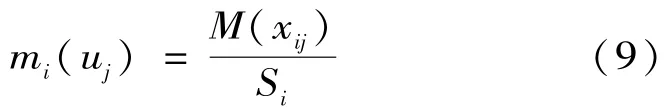
而證據xi在整個目標系統下的不確定的信度函數分配為:

經過驗證，上述對信度函數分配的定義滿足其定義，在已知樣本的情況下就可利用下一節提到的數據處理方法得到各信度函數分配值。

3 數據處理

面對大量的歷史數據，需要對其進行處理才能得到每一條證據在各目標模式下的μ和σ這兩個參數值。文獻［10］中給出了這兩個參數的估計方法，其中最常用的是最大似然估計法。設總體X服從參數為μ和σ2的對數分布，X1，X2，…，Xn為來自X的隨機樣本，那么μ和σ2的最大似然估計量為:

4 實例分析

變壓器是發電廠的重要設備，一旦發生故障則需盡快查出故障原因，進行維修，將損失減小到最低程度。然而，變壓器結構較復雜，難以根據表面現象判斷故障原因。目前最常用的方法就是根據變壓器油中提取的5種氣體的含量信息進行融合診斷。這5種氣體分別為:H2，CH4，C2H6，C2H4，C2H2。因此，可將這5種氣體作為證據，而根據變壓器最常見的故障類型將識別框架定義為:Θ=｛T1，T2，T3，D1，D2，PD｝，此識別框架的基元分別代表:低溫過熱、中溫過熱，高溫過熱、低能放電、高能放電、局部放電［11］。

根據文獻［7］提供的電力變壓器DGA數據，應用以上數據處理方法，得到數據樣本的參數，如表1所示。

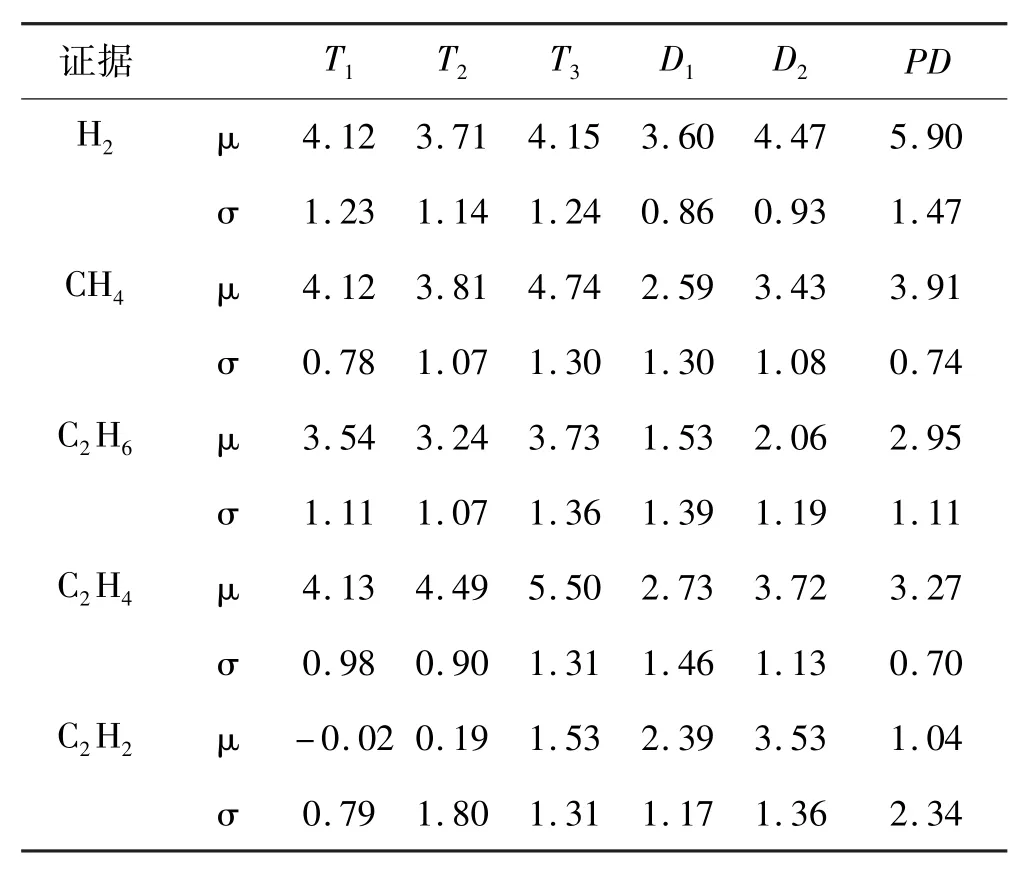
表1 數據樣本的平均值及標準差

如某電廠變壓器油中檢測到的5種特征氣體（H2、CH4、C2H6、C2H4、C2H2）含量分別為: 35.61，97.25，21.46，152.47，0.9，單位為μL/L，將上述信度函數分配的構造方法對數據進行處理，可得到每條證據在識別框架下的信度密度值M（xij），在表格中簡單記為Mi，將其列于表2中。

在得到各信度密度值之后應用上述提出的信度函數分配構造方法及聯合規則得到的中間結果和最終結果列于表3中。信度函數分配mi（uj）在表格中簡單記為mi，表中“融合12”代表第1、2種氣體信度函數的融合結果，以此類推。

由融合診斷結果可知，變壓器的故障類型為高溫過熱，與文獻［7］提供的診斷結果一致，并且降低了不確定度，說明了該方法的有效性。

日本的月岡、大江等人［12］提出當熱點溫度高于400℃時，估算熱點溫度的經驗公式為:

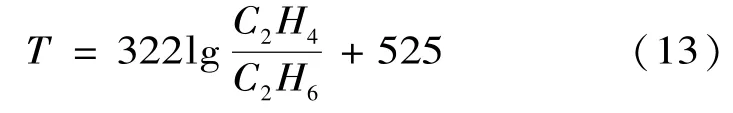
計算得出熱點溫度為799℃。

當故障點或故障部分的溫度處于600～800℃之間時，故障多為鐵芯多點接地［12］。故障點具體位置的查找目前多采用電氣測試法。

由表3中的計算結果可知，隨著證據的加入，某一模式的融合結果逐漸增大并成為最終融合結果中的最大值，再一次說明了融合診斷結果比單一診斷結果的可靠性要高。

5 結論

提出了一種基于D-S證據理論的信度函數分配的構造方法，并將其應用于變壓器故障診斷中。通過中間融合結果和最終融合結果的比較可知，當證據越多時，計算結果越可靠，但會增加計算量。為了得到較為精確的結果，應盡量使用原始數據，減少中間結果的使用次數。

［1］ 潘泉，程詠梅，梁彥，等.多源信息融合理論及應用［M］.北京:清華大學出版社，2013.

［2］ 朱大奇，于盛林.基于D-S證據理論的數據融合算法及其在電路故障診斷中的應用［J］.電子學報，2002，30（2）:221-223.

［3］ 田亮，常太華，曾德良，等.基于典型樣本數據融合方法的鍋爐制粉系統故障診斷［J］.熱能動力工程，2005，20（2）:163-166.

［4］ 楊靜，田亮，趙愛軍，等.基于典型樣本的證據理論信度函數分配構造方法［J］.華北電力大學學報，2008，35（5）:70-72，77.

［5］ 趙亮宇，田亮，王琪，等.基于改進信度函數分配方法的煤種判別技術［J］.華北電力大學學報，2011，38（4）:71-75.

［6］ 齊政，楊以涵，張宏宇.基于D-S證據理論的小電流接地故障連續選線方法［J］.華北電力大學學報，2005，32（3）:1-4.

［7］ 尹金良.基于相關向量機的油浸式電力變壓器故障診斷方法研究［D］.北京:華北電力大學，2013.

［8］ 張志國.小樣本條件下對數正態分布均值置信區間［J］.齊齊哈爾大學學報（自然科學版），2008，24（4）:75-78.

［9］ 吳石林，張玘.誤差分析與數據處理［M］.北京:清華大學出版社，2010.

［10］ 于洋.對數正態分布的幾個性質及其參數估計［J］.廊坊師范學院學報（自然科學版），2011，11（5）: 8-11.

［11］ 張利偉，苑津沙.基于典型樣本和證據理論的變壓器故障診斷［J］.電測與儀表，2013，（8）:14-19.

［12］ 丁軍.大型變壓器鐵芯多點接地的處理探討［C］.//第四屆安徽科技論壇安徽省電機工程學會分論壇論文集.馬鞍山電機工程學會，2006:397-411.

Method of Constructing Confidence Function Distribution Based on Typical Sample

Wang Xia，Tian Liang
（School of Control and Computer Engineering，North China Electric Power University，Baoding 071003，China）

The value of D-S evidence theory of belief function assignment is the key to get accurate fusion results，while traditional methods，such as the belief function assignment got through the usage of the membership function and the normal distribution，tend to be more subjective.In order to make the belief function assignment more objective.This paper puts forward a method constructing belief function assignment after combining other methods and analyzing the typical samples.First，samples were collected for each target mode，and which probability distributions the evidence of each mode obeys was judged.Then，the probability density of each piece of evidence was calculated by using corresponding probability formula.Finally，normalized processing was carried on，and the union rule was used to obtain the fusion results.The example shows that using this method can get more accurate results of fusion，and this method can not only improves the accuracy of the result of discrimination，but also reduce the uncertainty.In addition，it proves that the fusion diagnosis has a higher reliability than a single data.

evidence theory；typical sample；probability density；belief function

TK223

A DOI:10.3969/j.issn.1672-0792.2015.05.003

2015-03-26。

國家重點基礎研究發展計劃（973計劃）（2012CB215203）；中央高校基本科研業務費專項資金（2014MS145）。

王霞（1990-），女，碩士研究生，研究方向為數據挖掘與信息融合，E-mail:1016228976@qq.com。