基于單聲矢量傳感器的語音信號時頻掩蔽盲分離改進算法

陳曉屹，王英民

（西北工業大學 航海學院，陜西 西安，710072）

基于單聲矢量傳感器的語音信號時頻掩蔽盲分離改進算法

陳曉屹，王英民

（西北工業大學 航海學院，陜西 西安，710072）

利用單聲矢量傳感器精確的測向能力，提出了一種基于波達方位估計（DOA）的語音信號盲分離改進算法。該算法在時頻域進行，采用基于混合馮·米塞斯分布的期望最大化算法對混合信號中各個源信號在每個時頻點的概率進行估計。基于此，針對高混響及信號方位較近時很難估計到均值的問題，提出了一種簡單、有效的改進算法，并在不同混響強度、不同方位差及不同混合信號數目情況下對其進行了仿真驗證。仿真結果表明，相較于二值時頻掩蔽和泛值時頻掩蔽，文中提出的改進算法在信號-失真率（SDR）和客觀感知質量（PESQ）兩方面均有較大提高。

語音信號盲分離； 聲矢量傳感器； 波達方位估計； 期望最大化算法

0　引言

語音信號盲分離在多個語音信號同時存在時僅根據接收傳感器接收到的混合信號盡可能恢復源信號，目前已廣泛應用于自動語音識別和電話會議等領域。

獨立分量分析（independent component analysis，ICA）［1］是經典的盲分離算法，它基于信號間互相獨立的假設，在接收傳感器數目不少于源信號數目和混響較小時有很好的分離性能，但在高混響環境分離效果急劇下降，且在欠定情況（接收傳感器數目少于源信號數目時）無法分離信號。近年來，欠定條件下如何成功分離信號成為研究的熱點及難點。

時頻掩蔽算法［2］則利用語音信號在頻域的稀疏特性，在欠定條件下仍具有較好的分離性能，根據掩蔽值計算方法不同分為二值時頻掩蔽和泛值時頻掩蔽2種。二值時頻掩蔽將每個時頻單元的能量完全保留至目標信號或完全拒絕，該算法參數設置簡單，運行速度快，但會影響分離信號的平滑度。而泛值時頻掩蔽則根據概率密度函數將每一個時頻單元均按一定概率保留至目標信號，比二值時頻掩蔽方法具有更低的估計風險，但參數估計的準確程度將決定信號分離的效果。

不同于傳統的聲壓傳感器，矢量傳感器由于可同時捕獲聲壓和質點振速信息，僅單個矢量傳感器即可獲得精確的方位信息。近年來基于矢量傳感器的高精度測向和語音信號增強算法被大量研究，但僅有很少文獻將其用于盲信號分離。

文中在介紹2種基于單矢量傳感器的時頻掩蔽盲分離算法的基礎上，提出一種改進的泛值時頻掩蔽語音信號盲分離算法。首先，針對高混響及信號間距離較近時估計源信號方位誤差增大問題，提出一種簡單且有效的改進算法；另外，目標信號在每個時頻單元的保留概率由馮·米塞斯混合模型估計得出，模型參數則通過期望最大化算法進行計算。試驗表明，文中提出的改進算法能更準確的對參數進行估計，從而在信號-失真率（signal-to-distortion ratio，SDR）和客觀感知質量（perceptual evaluation of speech quality，PESQ）兩方面均可以有效提高語音信號的分離性能［1］。

1　單矢量傳感器方位估計

研究集中在2D（x-y）平面，即假設接收傳感器和各源信號位于同一個平面。矢量傳感器由1個聲壓傳感器和2個振速傳感器組成，可同時獲得聲壓信息（p0（t））和對應于x-和y-方向的振速分量（vx（t），vy（t））。假設有N個源信號sn（t），n=1，…，N，則單個矢量傳感器接收到的混合信號可以表示為

式中: N為源信號數目； ?為卷積； 第n個信號到矢量傳感器各分量間沖激響應用［hn（t），hn（t），hn（t）］T

0xy表示。

由聲學理論可知［3］，當信號在準靜態、各向同性介質中傳播，且滿足如下假設: 1） 平面波假設，即波長遠遠小于信號源到矢量傳感器間的距離； 2） 信號源窄帶假設，即信號頻譜為有限值。

則根據歐拉公式可得聲場中質點振速分量和壓強分量滿足如下關系

式中: v （t）=［vx（t），vy（t ）］T表示對應于x-和y-方向的質點振速； ρ0表示介質密度，c表示聲速；u=［cosθ，sinθ］T為單位向量，θ表示方位角。

由于語音信號在頻域比時域更滿足稀疏特性，即可以假設每個時頻點最多只有1個源信號，因此首先將矢量傳感器接收到的混合信號各分量（p0（t），vx（t），vy（t））分別進行短時傅里葉變換得到（P0（f，τ），Vx（f，τ），Vy（f ，τ）），則每個時頻點對應的方位值θ（f，τ）可表示為

式中: f和τ分別表示頻率點和時間滑窗位置；?［·］表示取實部。

2　基于方位信息的時頻掩蔽盲分離算法

時頻掩蔽方法是一種常用的盲分離算法，它通過計算不同信號在每一個時頻點的掩蔽值Mn（f，τ）作為接收端混合信號譜的權值，將信號分離開來，即

最后對Yn（f，τ）進行逆短時傅里葉變換，得到分離信號的時域形式yn（t）。根據計算Mn（f，τ）方法的不同，可分為二值時頻掩蔽和泛值時頻掩蔽2種。其中二值時頻掩蔽每個時頻點取值為1或0，表示接受或拒絕對應時頻點的信息，泛值時頻掩蔽則通過概率密度分布計算將各時頻點保留至目標信號的概率，取值范圍為［0，1］。

2.1基于方位信息的二值時頻掩蔽

對每個時間序列τ，提取θ（f，τ）的直方圖N個最大的峰值所對應的方位值，并將其作為N個源信號的方位ηn（τ），n=1，…，N。

則用于分離第n個信號的二值時頻掩蔽為［4］

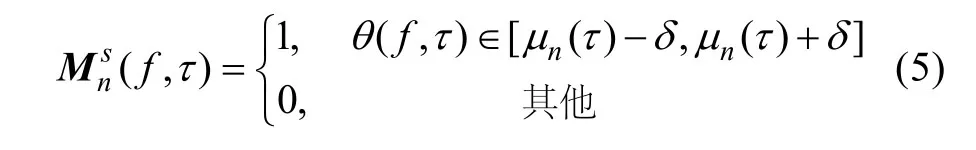
其中，δ表示式（3）所得方位值的可靠范圍。若θ（f，τ）距所有源信號ηn的方位差均在δ之外，該時頻點的方位值被認為屬于以下3種情況之一: 1） 計算誤差； 2） 混響的影響； 3） 該時頻點同時存在多個信號互相影響，則對應時頻點的掩蔽值被設定為0。在文獻［4］中，取δ=4°。

2.2基于方位信息的泛值時頻掩蔽

由于方位信息的循環特性，引入馮·米塞斯概率密度分布函數，以此計算不同信號在每個時頻點的貢獻。馮·米塞斯分布又被稱為循環高斯分布，其概率密度函數表示為

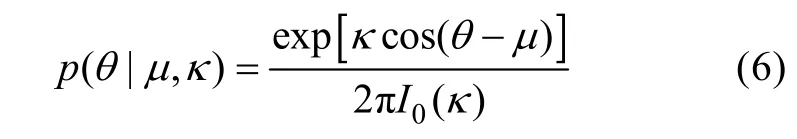
式中: -π≤η＜π表示方位均值； 1/κ表示會聚參數，分別對應于正態分布中的均值與方差；I0（κ）表示階數為0的修正貝塞爾函數。

由式（3）計算得到的θ（f，τ）屬于第n個信號的概率

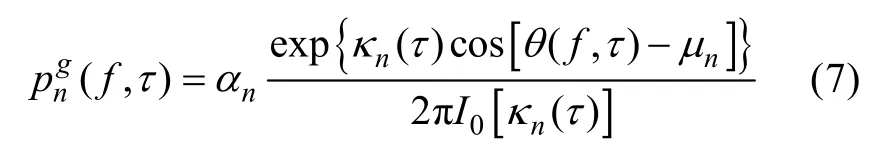
式中:κn（τ）表示時間序列τ時對應于第n個信號的會聚參數； αn表示第n個信號的概率，一般取1/N。

在文獻［5］中，作者假定N個源信號方位已知，且發現κn值與6 dB帶寬θnBW有如下關系

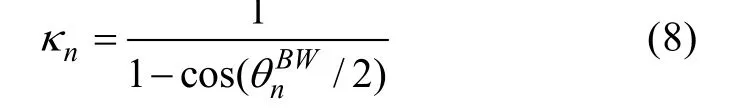
因此，在每個時間序列τ，將θnBW從10°～180°每隔10°循環一次，與時間序列為τ的方位直方圖進行擬合，選擇擬合效果最好時對應的κ值作為κn（τ），則信號n對應的泛值時頻掩蔽Mg（f，τ）可以表示為［5］n

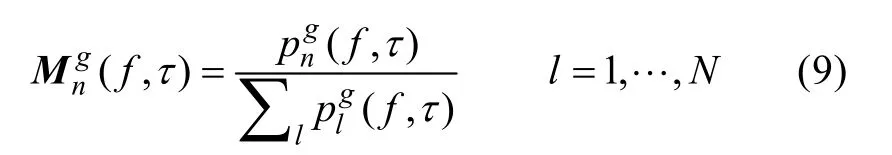
3　改進的泛值時頻掩蔽盲分離算法

由于二值時頻掩蔽方法僅有0或1兩種取值，因此在相鄰時間窗會發生取值跳躍現象，由此引起信號失真，采用泛值掩蔽能較好地避免失真現象。但上述泛值掩蔽算法假定方位信息已知，這在實際工作中很難滿足，且對所有可能值循環求κ值也大大增加了計算量。針對上述問題，文中提出一種估計信號方位的改進算法，并且引入EM算法對κ值進行數學估計，最后通過仿真試驗證明了改進算法的有效性。

3.1估計信號方位的改進算法

通過2.1節可知，信號方位可通過提取θ（f，τ）在不同時間序列τ峰值所在位置獲得，但實際上并非所有時間窗均可得到N個峰值，可能的原因主要有: 1） 某些時間段僅有某個或部分信號活躍； 2） 源信號方位過于接近造成混疊； 3） 混響較大將某個或某些信號淹沒。如圖1（a）所示，當無混響或混響較小，并且源信號方位距離較遠時，峰值易于提取，當混響較大且信號方位接近時，峰值信息由于混疊難以估計，如圖2（a）所示。

基于此，文中首先提取每個時間段τ的峰值所在位置θest（m，τ）（m≤N），將所有θest（m，τ）的直方圖對應的N個峰值位置作為N個源信號的方位ηn，n=1，…，N，如圖1（b）和圖2（b）所示，在高混響且信號方位靠近時仍能準確估計各個源信號方位。

3.2基于EM算法的參數估計算法

EM算法的基本概念為通過循環E步驟和M步驟尋找一組參數集合Θ=｛αn（τ），κn（τ）｝，使其最大限度的擬合θ（f，τ），即

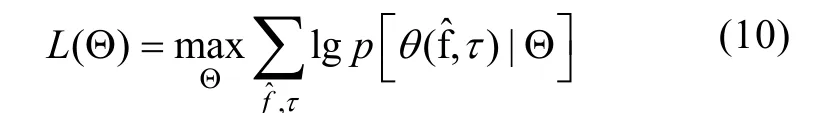
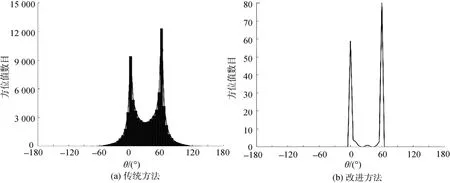
圖1　無混響且2個語音信號分別在0°和60°時的直方圖Fig. 1　The histogram without reverberation when two speech sources are located respectively at 0° and 60°

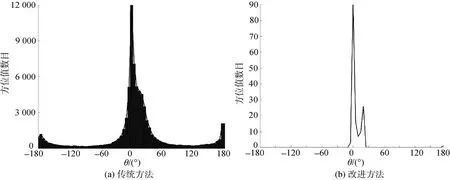
圖2　混響為0.3 s且2個語音信號分別在0°和20°時的直方圖Fig. 2　The histogram with reverberation（0.3 s） when two speech sources are located respectively at 0° and 20°

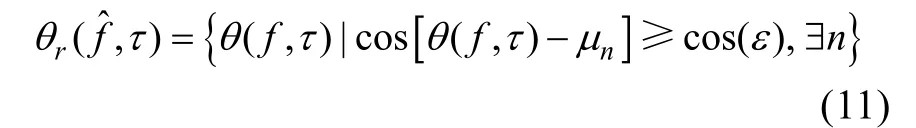
在E步驟，由給定參數的初值或在M步驟得到的參數Θ，第n個信號在可靠時頻點的后驗概率由馮.米塞斯概率分布函數估計得到，非可靠時頻點的概率值均設為0，即

其中: 符號“∝”表示對N個信號的后驗概率進行歸一化； V表示馮.米塞斯概率函數。

在M步驟，利用E步驟得到的歸一化概率νn（f，τ）對參數進行更新，即

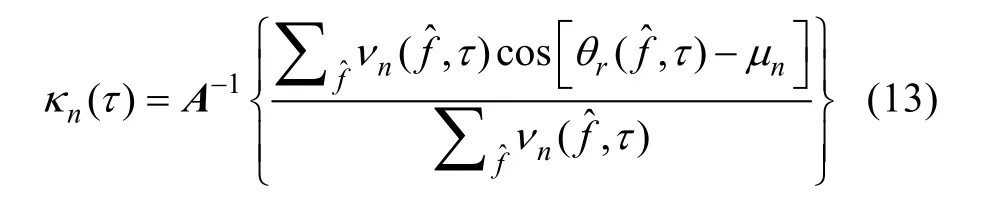
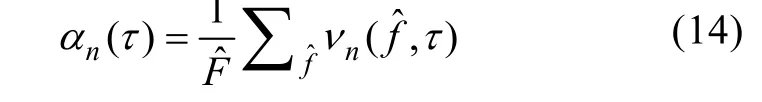
式中:A-1表示用Batschelet表格估計會聚參數的函數［6］；表示每個τ值對應可靠頻率點的數目。

算法重復E、M步驟直到收斂，此時時頻掩蔽值

4　算法驗證及結果分析

為了驗證改進算法的分離效果，對單個矢量傳感器在2個（s1，s2）及3個（s1，s2，s3）語音信號混合的情況下分別進行仿真。混合信號由源信號與傳輸函數卷積得到，其中所有語音信號均從TIMIT語音數據集中隨機選取，傳輸函數通過成像算法［7］進行仿真。

矢量傳感器被放置在1個9×6×3 m3的房間正中央，麥克風均距其1 m且保持相同高度（1.5 m）。混響時間T60從0～0.5 s每隔0.1 s仿真1次，每個混響情況下，信號s1都維持在0°位置，相鄰信號方位差Δθ則從10°～90°每隔10°仿真1次。

采用SDR和PESQ來評估分離性能。每種試驗環境（不同混響時間，不同方位差）均重復15次隨機語音源選擇并計算平均值。

SDR通常用dB表示，用源信號的能量與分離信號中不屬于該信號的能量比值來衡量，即

圖3和圖4分別表示2個和3個語音混合信號時通過式（16）計算的SDR結果，其中“混合信號”代表未經處理的輸入信號，“二值時頻掩蔽”和“泛值時頻掩蔽”分別代表2.1節、2.2節的對比算法，“改進的泛值時頻掩蔽”代表文中提出的算法。為了得到SDR分別隨混響（T60）和方位差（Δθ）的變化趨勢，首先將每個混響條件下Δθ從10°～90°對應的SDR值平均，結果如圖3（a）和圖4（a）所示。

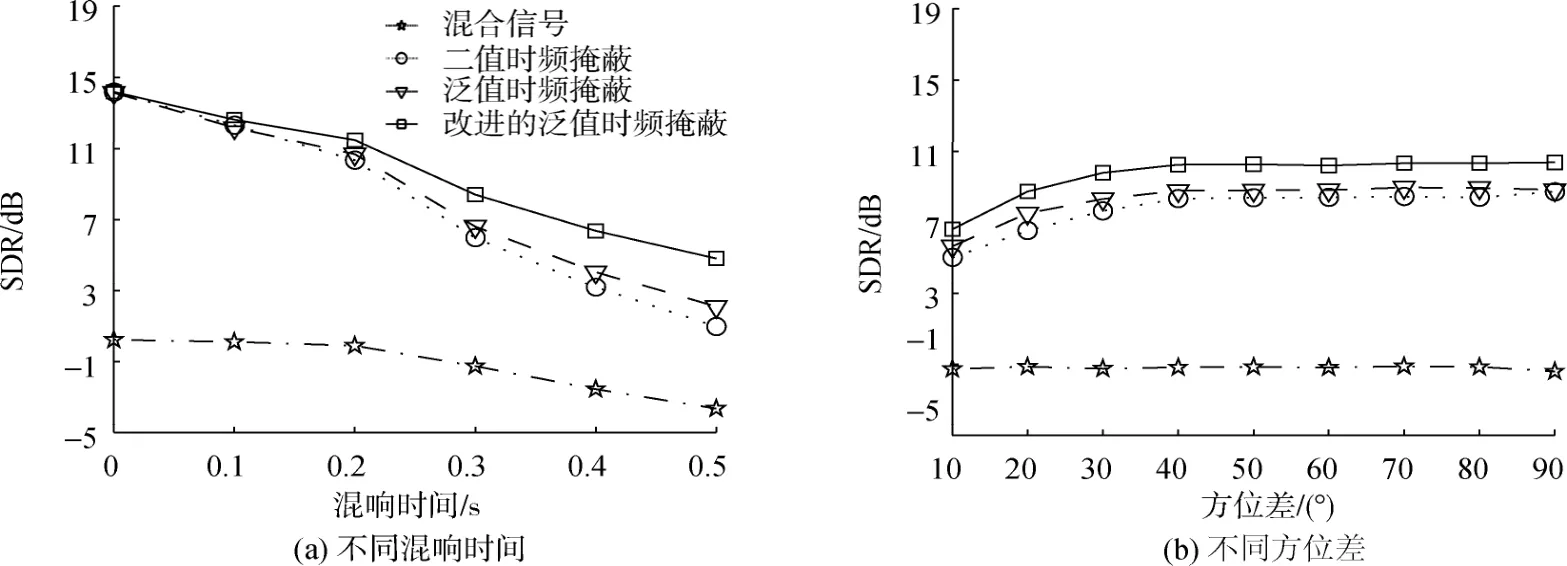
圖3　2個語音信號混合時不同算法計算的信號失真率（SDR/dB）隨混響時間和方位差變化曲線Fig. 3 Curves of the signal-to-distortion ratio（SDR/dB） obtained by different methods versus reverberation time and azimuth error for the mixture of two speech sources

圖4　3個語音信號混合時不同算法計算的SDR/dB隨混響時間和方位差變化曲線Fig. 4　Curves of the SDR/dB obtained by different methods versus reverberation time and azimuth error for the mixture of three speech sources

類似地，當源信號放置在固定方位差位置時T60從0～0.5 s 分離得到的SDR平均，結果如圖3（b）和圖4（b）所示。從圖中可以看出，相對于方位差，分離效果受混響影響更大，當T60大于0.2 s時，SDR值明顯下降。但幾乎在所有情況下，文中提出的改進算法均優于其他2種對比算法，尤其在混響較強時優勢明顯。

PESQ由國際電信聯盟組織提出，用于評價客觀（mean opinion score，MOS）值［8］。由于PESQ得分與人耳感知質量高度一致，故常用于評估分離效果。PESQ值分布于-0.5～4.5間，得分越高說明感知質量越好。圖5和圖6分別表示不同數量混合信號時對應的PESQ結果，相對于2種對比算法，文中提出的改進算法可以獲得更高的感知質量。

圖5　2個語音信號混合時不同算法計算的客觀感知質量（PESQ/MOS）隨混響時間和方位差變化曲線Fig. 5　Curves of the perceptual evaluations of speech quality（PESQ/MOS） obtained by different methods versus reverberation time and azimuth error for the mixture of two speech sources

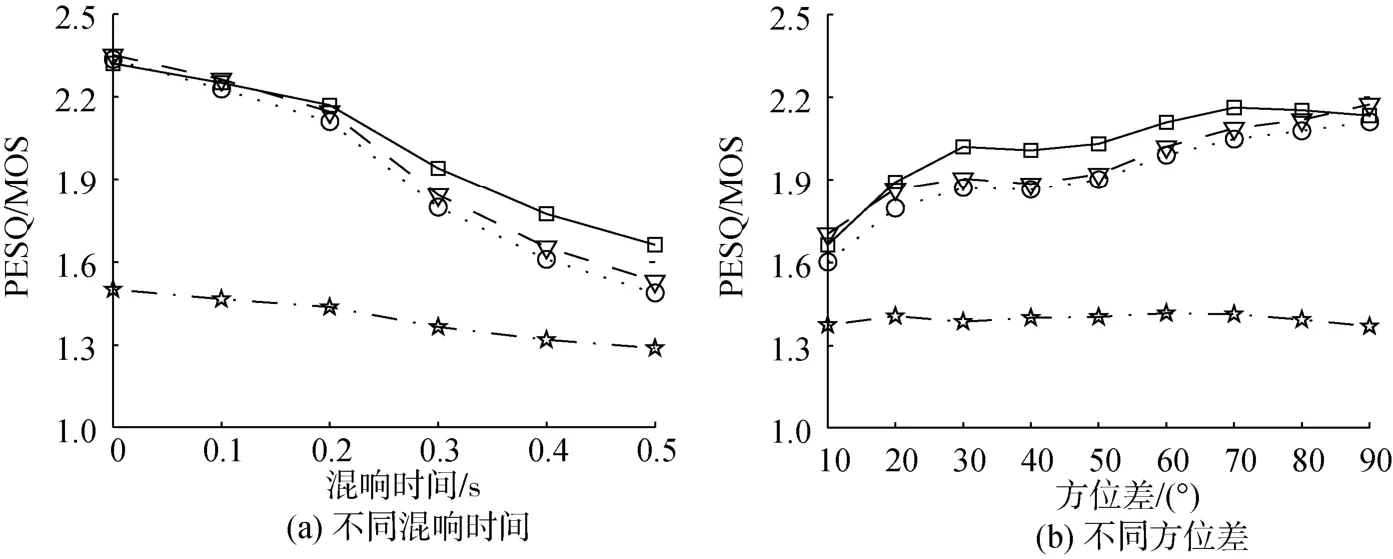
圖6　3個語音信號混合時不同算法計算的PESQ/MOS隨混響時間和方位差變化曲線Fig. 6　Curves of the PESQ/MOS obtained by different methods versus reverberation time and azimuth error for the mixture of three speech sources

5　結束語

文中提出一種基于單矢量傳感器的泛值時頻掩蔽盲分離的改進算法，該算法在高混響及源信號方位接近時仍能精確估計方位信息，并引入期望最大化算法對會聚參數進行估計。試驗結果表明，該算法在SDR和PESQ兩方面均可有效提高信號分離性能。

［1］Comon P，Jutten C. Handbook of Blind Source Separation: Independent Component Analysis and Applications［J］. IEEE Signal Processing Magazine，2010，30（2）:133-134.

［2］Yilmaz O，Rickard S. Blind Separation of Speech Mixtures via Time-Frequency Masking［J］. IEEE Transactions on Signal Processing，2004，52（7）: 1830-1847.

［3］Nehorai A，Paldi E. Acoustic Vector-Sensor Array Processing［J］. IEEE Transaction on Signal Processing，1994，42（9）: 2481-2489.

［4］Shujau M，Ritz C H，Burnet I S. Separation of Speech Sources using an Acoustic Vector Sensor［C］//IEEE International Workshop on Multimedia Signal Processing，2011.

［5］Gunel B，Hachabiboglu H，Kondoz A M. Acoustic Source Separation of Convolutive Mixtures based on Intensity Vector Statistics［J］. IEEE Transactions on Audio，Speech and Language Processing，2008，16（4）: 748-756.

［6］Hung W L，Chang-Chien S J，Yang M S. Self-Updating Clustering Algorithm for Estimating the Parameters in Mixtures of von Mises Distributions［J］. Journal of Applied Statistics，2012，39（10）: 2259-2274.

［7］Allen J B，Berkley D A. Image Method for Efficiently Simulating Small-Room Acoustics［J］. Journal of the Acoustical Society of America，1979，65（4）: 943-950.

［8］Thiede T，Treurniet W C，Bitto R. PEAQ-The ITU Standard for Objective Measurement of Perceived Audio Quality［J］. Journal of the Audio Engineering Society，2000，48（1）: 3-29.

（責任編輯: 楊力軍）

An Improved Blind Speech Separation Algorithm via Time-frequency Masking Based on a Single Acoustic Vector Sensor

CHEN Xiao-yi，WANG Ying-min
（School of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China）

An improved blind speech separation algorithm is presented based on the direction of arrival（DOA） estimation，which is obtained by the precise direction finding ability of a single acoustic vector sensor（AVS）. The proposed algorithm works in time-frequency domain，in which the probability at each time-frequency unit of a specific source is estimated via an expectation-maximization（EM） algorithm based on the von Mises distribution mixture model. Because the mean value is difficult to estimate when the reverberation level is high or the sources are placed closely，a simple but effective improved algorithm is proposed，and is verified via simulation under different reverberation level，direction difference and source number. Simulation results show that the improved algorithm is superior to the binary time-frequency masking algorithm and the soft time-frequency masking algorithm in terms of signal-to-distortion ratio（SDR） and perceptual evaluation of speech quality（PESQ）.

blind speech separation； acoustic vector sensor（AVS）； direction of arrival（DOA） estimation； expectation maximization（EM） algorithm

TJ630.34； TB556

A

1673-1948（2015）02-0098-06

2014-12-02；

2015-01-05.

陳曉屹（1986-），女，在讀博士，研究方向為信號與信息處理.