基于SIFT特征與預測的運動目標檢測算法

吳忠良　余升

摘 要： 為了在動態場景下對運動目標進行快速檢測，提出一個改進的SIFT特征匹配的檢測算法。首先采用SIFT方法提取匹配的特征點；然后為全局運動建立起旋轉參數模型，并使用RANSAC方法排除外點的影響，運用最小二乘法求解全局運動參數；最后利用基于殘差圖像塊的更新策略對特征點進行更新。該算法是基于預測的SIFT特征點匹配算法，不僅保持了SIFT方法的優越性能，而且提高了檢測目標的速度。與塊匹配算法的實驗結果對比表明，該算法可以實時準確地檢測出運動目標。

關鍵詞： 目標檢測； SIFT特征； 旋轉參數模型； 動態場景

中圖分類號： TN911.73?34； TP391 文獻標識碼： A 文章編號： 1004?373X（2015）19?0087?04

Abstract： An improved detection algorithm of SIFT feature marching is provided for rapid detection to moving object in dynamic scene. The matched feature points are extracted by SIFT method， and the rotation parameter model is established for global motion. The influence of exterior points is eliminated by RANSAC method. The global motion parameters are solved by the least square method， and the feature points are updated by the updating strategy based on residual image block. This matching algorithm is based on the predicted SIFT feature points， which can remain the high performance of SIFT method and improve the detection rate of the object. Compared with the experimental results of block matching algorithm， it demonstrates that this algorithm can detect moving object accurately and in real?time.

Keywords： object detection； SIFT feature； rotation parameter model； dynamic scene

0 引 言

現代監控系統中，需要對運動目標進行實時快速的檢測，傳統的固定攝像機由于其監控范圍有限，逐漸被可旋轉的攝像機代替。動態場景下的圖像不斷變化，信息處理相對靜態場景更加復雜，因此動態場景下目標檢測的研究具有重要的意義。目前檢測運動目標的方法主要有：時間差分法[1]、光流法[2]、背景減除法[3]、匹配的方法[4]等。時間差分法對環境有著較強的適應性，但由于不能對檢測的所有特征進行提取，無法全部的對目標區域進行檢測；光流法適用范圍較廣，但該算法較為復雜，運算量很大，不適合實時的檢測動態場景下的運動目標；背景減除法可提供完整的目標特征，但該方法容易產生離散噪聲點，并且容易受到光照和灰度等級變化的干擾，需要建立背景模型對背景圖像進行實時更新；特征點匹配的方法，在相鄰幀中分別提取特征點，并匹配特征點，再利用匹配的特征點對求解全局運動參數。由于特征點匹配的方法適合攝像機隨意轉動的情況，而且只需要對某些有特征的、穩定的點進行計算，大大提高了算法速度。所以本文采用特征點匹配的方法。

SIFT特征點由David Lowe于1999年首次提出[5?6]，此方法對檢測目標的旋轉、尺度縮放、視角變化及亮度變化具有良好的不變性，并對遮擋和噪聲也有很好的魯棒性。匹配點多而且穩定也是該算子的一個重要特點。由于SIFT在用于攝像機運動參數求解時運算量較大，難以達到實時性的要求，因此，本文針對實時性檢測的需要，在SIFT算法的基礎上加以改進，提出了基于預測的SIFT特征點匹配算法，可以實時快速地檢測出運動目標。

1 SIFT特征點

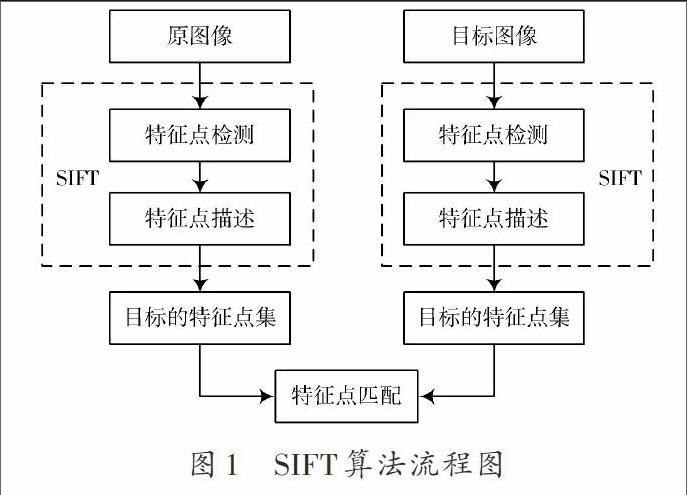
SIFT算法是一種提取局部特征的算法，該算法的主要思想就是在圖像中提取出特征點，使圖像的匹配轉化為特征點向量的相似性度量。SIFT 特征匹配算法主要有三個步驟：SIFT特征點的檢測；SIFT特征描述符的生成；SIFT 特征向量的匹配。算法過程如圖1所示。

SIFT算法通過比較圖像灰度值得到特征向量，特征提取是SIFT算法的重點。特征的提取包括初步定位特征點，精確定位特征點，為每個特征點明確方向和生成關鍵點描述算子。一般提取越多的圖像特征，越能反映出圖像中目標的真實特征，匹配的結果也會更加精確，但會增加算法的復雜性和運算時間。為了達到實時性的效果，特征的提取并非越多越好，SIFT算法只需要很少的必要的特征匹配點，就可以很好地對特征進行匹配。

2 快速檢測匹配算法

2.1 求解全局運動參數

對運動目標的檢測需要消除攝像機的移動影響。攝像機的主要運動方式有平移、旋轉、縮放和俯仰，需要運用合適的全局運動模型及運動參數，運用比較廣泛的有仿射參數模型和旋轉參數模型[7?8]。仿射參數模型相對簡單，適合攝像機旋轉運動較小時的情況；旋轉參數在攝像機旋轉角度較大時可以更好地描述攝像機的運動，因此采用8參數旋轉模型[9]，滿足攝像機的各種運動情況。endprint

式中：參數[A]為旋轉參數矩陣，主要由攝像機的旋轉和平移參數決定，同坐標參數無關。實際中無法得知攝像機的旋轉角度和平移量，需要通過其他方法求解矩陣[A。]

使用特征點匹配全局運動參數的思想是：在相鄰兩幀中分別搜索特征點，再對特征點對匹配，得到[F=f1， f2，…， fn，…， fN，]表示匹配點對的集合，其中[fn=（Xt-1，n，Xt，n）]為第[n]對匹配點，并用最小二乘法求最優解。

運用特征點進行運動補償時，匹配的結果可能是失真的，即發生誤匹配。失真的點又稱作外點。相對來說，產生外點的概率較小，但為了避免引入外點造成全局運動的估計發生較大偏差，需要采取方法將外點從數據點中去除。因此采用RANSAC[10?11]（隨機抽樣一致）的方法去除誤匹配點，使用該方法后再利用最小二乘法[12]便可求解出較為準確的參數矩陣。

2.2 基于預測的特征點匹配算法

攝像機拍攝所得的圖像序列中，每兩個幀之間的間隔時間很短，幀之間的變化很小，相差一般只有幾個像素。由于當前幀包涵了下一幀的大量信息，據此提出基于預測的快速匹配方法，即根據當前幀的特征點對下一幀的特征點進行預測。該算法根據預測的特征點的位置，小范圍的搜索特征點，得到當前幀的特征點。具體步驟如下：

（1） 設第[t-1]幀圖像的特征點集為[Pt-1={pt-1，1，pt-1，2，…，pt-1，m}]；

（2） 根據特征點[pt-1，m]和運動參數，預測[t]幀的特征點[pt，m；]

（3） 以特征點[pt，m]為圓心，在半徑為[N]個像素的圓內搜索特征點[pt，n]。將[pt，n]與[pt-1，m]進行匹配，若匹配成功，則建立匹配點對[ft，n=（pt-1，m，pt，n），]即可得到匹配點對的集合[Ft={ft，1， ft，2，…， ft，n，…， ft，N}]以及第[t]幀的特征點集[Pt={pt，1，pt，2，…，pt，n，…，pt，N}]。

這種預測下一幀的方法使匹配在限制的范圍內進行，縮小了搜索的范圍，減少了誤匹配的發生。其中[N]值的大小直接關系到運算量的大小，通過在多組動態場景下拍攝視頻的實驗，確定[N=3]時效果最佳。

2.3 基于殘差塊的特征點更新

在動態場景下，攝像機拍攝的視角會不斷變化，圖像的特征也隨之變動，故此需要對特征點進行及時更新。可以設一個最低匹配值[Tf]，當特征點的匹配數低于[Tf]時就立刻更新。[Tf]設置較大會造成運算量過大，影響算法效率；設置較小會使平均匹配點數降低，造成最小二乘解不準確。根據多組試驗選取最佳[Tf=15]。

特征點的更新需要對圖上的點進行搜索，由于特征點主要集中在檢測目標中且在求解運動參數時，真正起作用的是背景點，所以需要將包括檢測目標即前景的一塊區域排除。

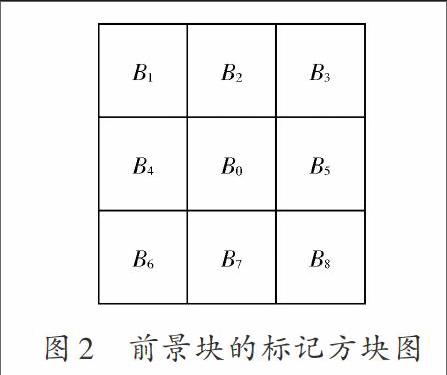
如圖2所示，采用基于殘差圖像的方法將前景區域進行快速標記。將殘差圖像分成[m×n]個大小的塊，計算每個塊的SAD[13]，并按大小進行排序。[SAD=i=0Mj=0Nψi，j，]其中[ψi，j]是[（i，j）]的殘差。圖2中，[B0]是當前預選前景塊，若鄰域8個圖像塊的SAD值有超過一半排在總SAD值的前30%，則將當前預選前景塊標記為前景塊，將每個預選前景塊都依次進行排查。塊參數[m]和[n]的取值決定了計算量的大小和前景塊標記的準確性，通過實驗確定設為[16×16]最為合適。

2.4 算法實現的具體步驟

若已知[pt-1，1]為第[t-1]幀的特征點集，[At-1]為第[t-1]幀的仿射參數矩陣。對第[t]幀運動目標進行檢測，其算法詳細步驟如下：

（1） 根據2.1節提出的方法搜索出第[t]幀所有特征點[pt，n]并保存在特征點集[Pt]中，并用[Pt-1]和[Pt]進行匹配并建立匹配點對[Ft]。

（2） 用RANSAC去除[Ft]中可能存在的誤匹配點，再用最小二乘法求解出[t]幀的仿射參數矩陣[At]。

（3） 利用式（2）對[t-1]幀圖像[It-1]中攝像機旋轉導致的運動進行補償，得到補償圖像[It]。再將補償圖像[It]和第[t+1]幀圖像[It]做背景差處理，得到殘差圖像[Iobj]。

（4） 判斷得到的[Pt]點集中的特征點數目是否小于[Nf]，若小于則用2.3節中的方法進行更新。

（5） 將得到的[Iobj，][At，][Pt]進行保存，并同時進行背景的實時更新。

3 實驗結果與分析

為了驗證算法的效果，將本文算法同塊匹配算法進行實驗對比。使用Visual Studio 2010在Intel i3 CPU內存4 GB的PC機的實驗平臺上進行調試。通過視頻實驗對結果進行比較和分析。具體的實驗結果如圖3和圖4所示。

圖3為分辨率為[320×240]的實拍圖像序列。圖3（a）為原圖像序列的第30幀和70幀，圖3（b）為塊匹配算法得到的實驗結果，圖3（c）為本文算法的實驗結果。通過對比可以看出，匹配算法檢測出的目標圖像較為模糊，輪廓有殘缺，背景中有東西沒被除去。本文算法檢測的目標圖像十分飽滿和清晰，完全排除了背景中的干擾。此實驗結果說明，本文算法繼承了SIFT算法的優越性，在攝像機快速旋轉時可以有效檢測運動目標。

圖4是對分辨率為[352×288]的標準序列的測試結果。從實驗結果可以看出，兩種算法都能檢測出目標。匹配算法檢測出的目標比較模糊，背景中的觀眾并沒有完全去除。由于攝像機的運動不僅僅是平移，匹配算法不能良好適應。本文算法測得的結果明顯較為清晰。通過此實驗可以說明，本文算法對攝像機在復雜的運動下檢測運動目標同樣適用。

表1是兩種算法的運行時間比較，可以看出本文算法耗時要小于塊匹配法，運行效率有了很大提高，說明本文算法十分適合實時檢測目標。該算法采用旋轉模型得到全局運動參數，并使用基于預測的方法可以測出比較清晰的運動目標，說明本文提出的算法具有很強的實用性。endprint

4 結 論

本文提出了一種基于預測的匹配算法，針對動態場景下的目標進行檢測。首先利用SIFT 算法提取出特征點，再構建全局運動模型來描述攝像機的運動，通過運用最小二乘法求解運動參數，其中采用RANSAC方法去除外點；最后基于殘差圖像塊的特征點更新策略保證求解參數的準確性。實驗結果證明，該算法可以準確實時地檢測出移動攝像機下的運動目標。

參考文獻

[1] 周若谷.基于高斯背景建模和時間差分法的目標檢測研究[J].電腦編程技巧與維護，2014（4）：28?29.

[2] 張瑜慧，沈洋.基于圖像融合的運動前景檢測方法[J].現代電子技術，2013，36（24）：67?69.

[3] 張詠，李太君，李枚芳.利用改進的背景差法進行運動目標檢測[J].現代電子技術，2012，35（8）：74?77.

[4] BOROS E， ROSCA G， IFTENE A. Using SIFT method for global topological localization for indoor environments [C]// Proceedings of 2010 the 10th IEEE Workshop of the Cross?Language Evaluation Forum. Corfu： IEEE， 2010： 277?282.

[5] LUO J， OUBONG G. A comparison of SIFT， PCA?SIFT and SURF [J]. International Journal of Image Processing， 2009， 3（4）： 143?152.

[6] 傅衛平，秦川，劉佳，等.基于SIFT算法的圖像目標匹配與定位[J].儀器儀表學報，2011，32（1）：163?169.

[7] 趙亞湘，樊曉平，劉少強.基于運動矢量場的運動目標區域檢測[J].光電子·激光，2014，25（12）：2387?2392.

[8] SU Y P， SUN M T， HSU V. Global motion estimation from coarsely sampled motion vector field and the applications [J]. IEEE Transactions on Circuits and Systems for Video Technology， 2005， 15（2）： 232?242.

[9] LOWE D G. Distinctive image features from scale?invariant keypoints [J]. International Journal of Computer Vision， 2004， 60（2）： 91?110.

[10] 郭紅玉，王鑒.一種基于RANSAC基本矩陣估計的圖像匹配方法[J].紅外，2008，29（2）：5?8.

[11] 曲天偉，安波，陳桂蘭.改進的RANSAC算法在圖像配準中的應用[J].計算機應用，2010，30（7）：1849?1851.

[12] 魯鐵定，陶本藻，周世健.基于整體最小二乘法的線性回歸建模和解法[J].武漢大學學報：信息科學版，2008，33（5）：504?507.

[13] HE Y W， FENG B， YANG S Q， et al. Fast global motion estimation for global motion compensation coding [C]// 2001 IEEE International Symposium on Circuits and systems. Sydney： IEEE， 2001， 2： 233?236.endprint