周期為2p2的四階二元廣義分圓序列的線性復雜度

杜小妮 王國輝 魏萬銀

?

周期為2p2的四階二元廣義分圓序列的線性復雜度

杜小妮 王國輝*魏萬銀

(西北師范大學數學與統計學院 蘭州 730070)

該文基于分圓理論，構造了一類周期為的四階二元廣義分圓序列。利用有限域上多項式分解理論研究序列的極小多項式和線性復雜度。結果表明，該序列具有良好的線性復雜度性質，能夠抗擊B-M算法的攻擊。是密碼學意義上性質良好的偽隨機序列。

流密碼；廣義分圓序列；線性復雜度；極小多項式

1 引言

偽隨機序列在擴頻通信、測量距離、雷達導航、CDMA通信、流密碼系統等領域有著極為廣泛的應用。在密碼學領域的應用中，偽隨機序列必須具有高的線性復雜度[1]。從安全的角度講，為抵抗已知明文攻擊，序列的線性復雜度必須足夠大。根據B-M算法[2]，一條好的序列往往要求它的線性復雜度必須不小于其周期長度的一半。

2 廣義分圓序列的構造

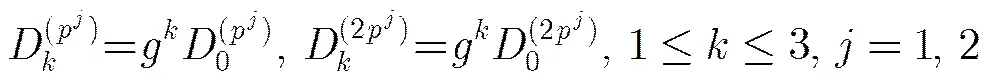
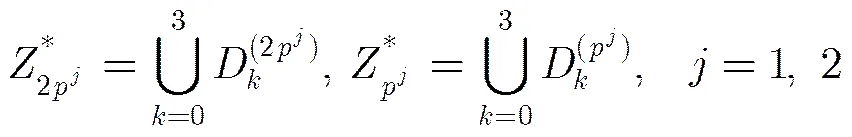
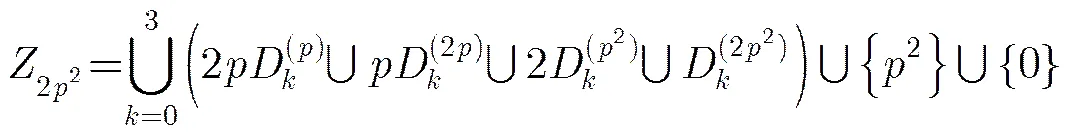
令

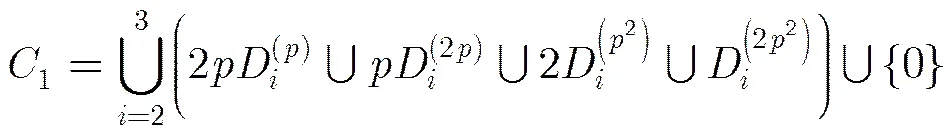
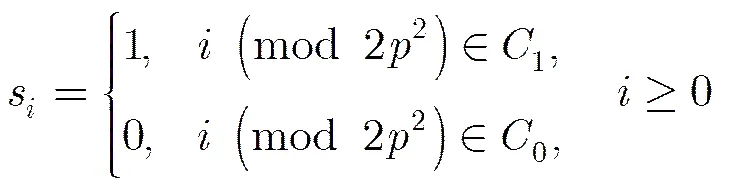
3 廣義分圓序列的線性復雜度

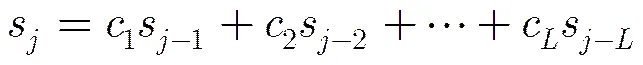
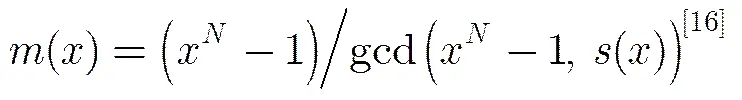
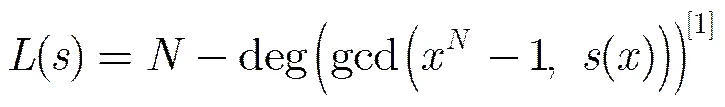
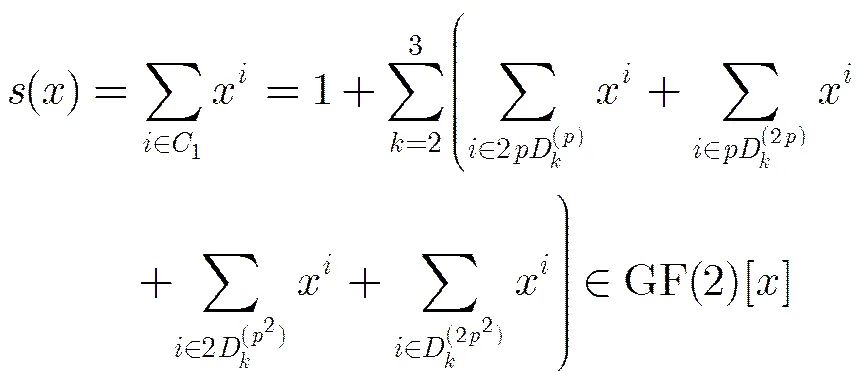
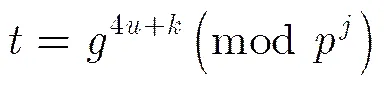
所以

證畢

證畢

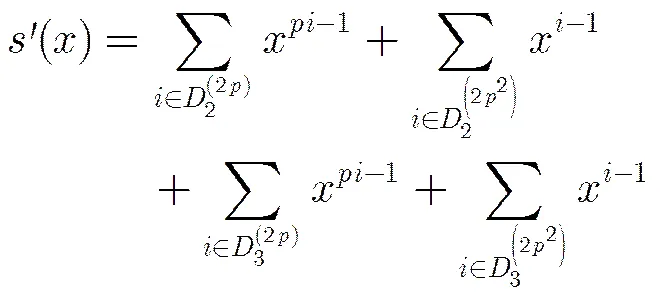
根據引理3及式(2)可得

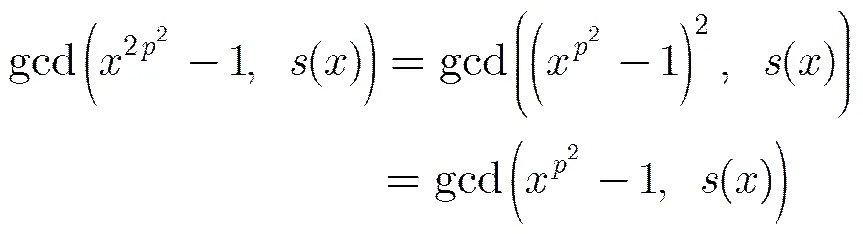
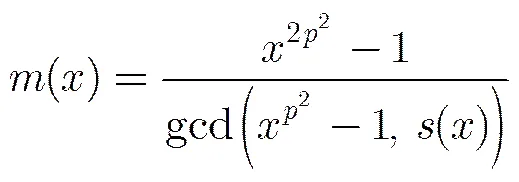
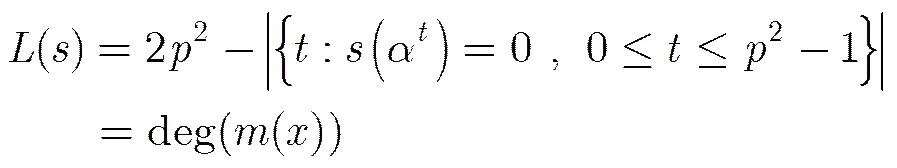
令

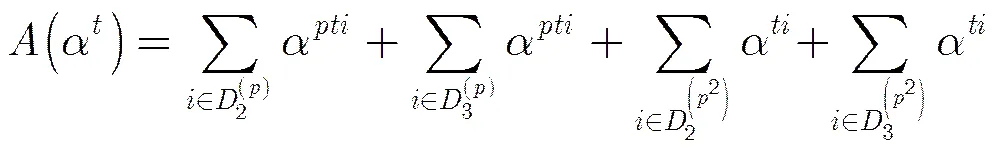
則

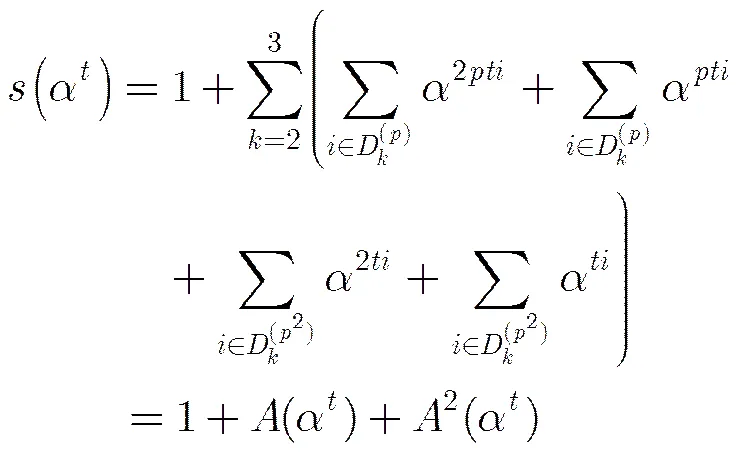
證畢

引理4[17]符號含義同上，則

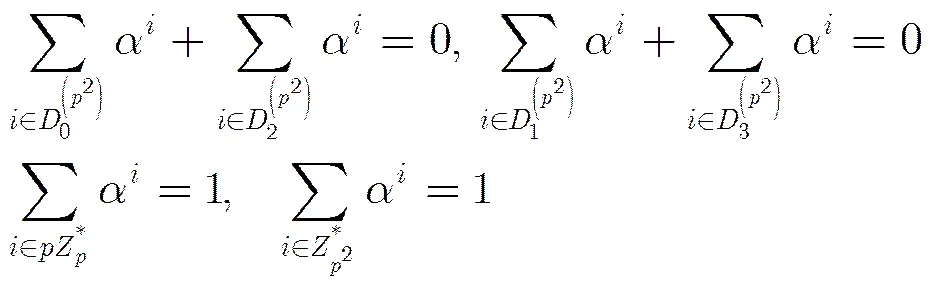
下文中令

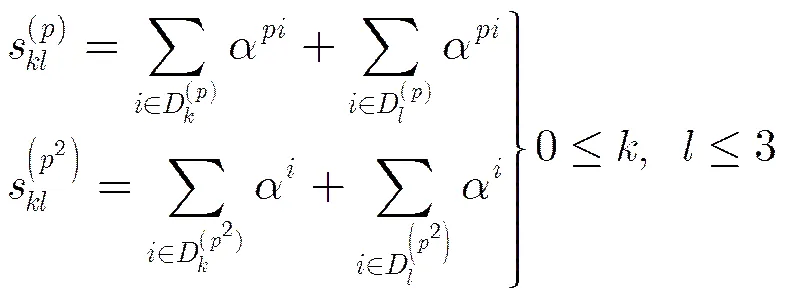
引理5 符號含義同上，則

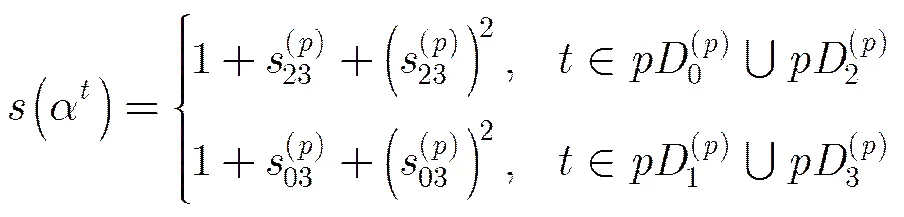
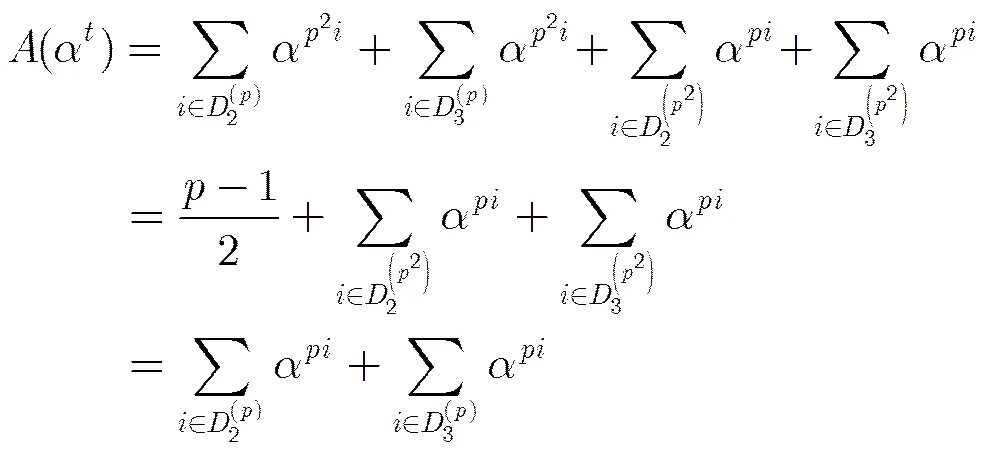
證畢

引理6 符號含義同上，則

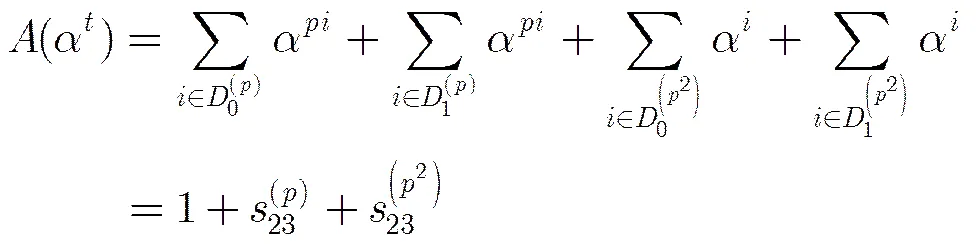
證畢

引理7[18]當且僅當,當且僅當。

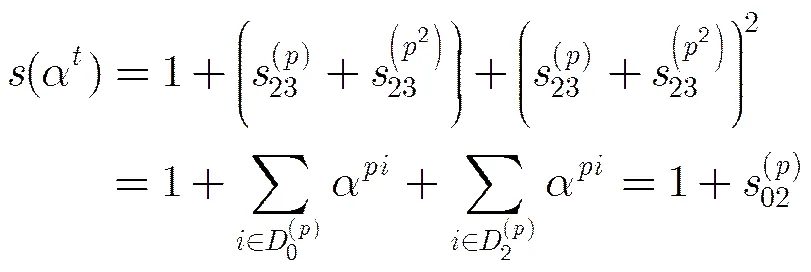
(2)的證明與(1)類似，在此省略。

證畢

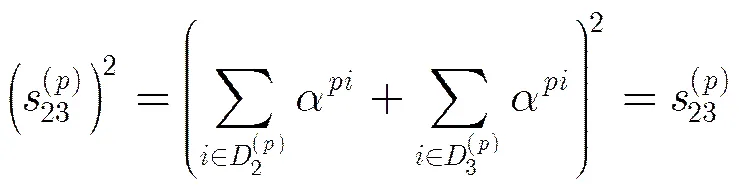
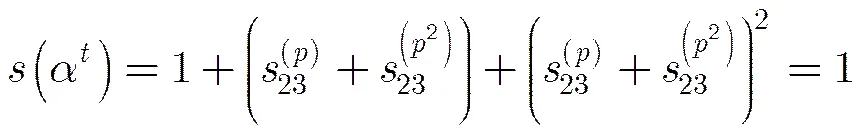
(2)的證明與(1)類似，在此省略。

證畢

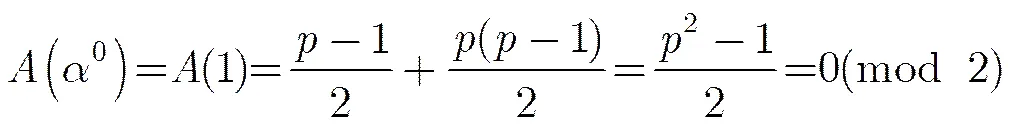
則

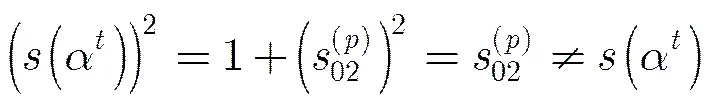
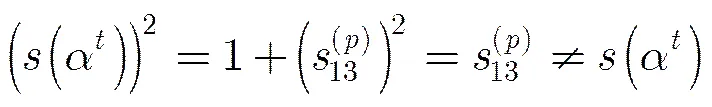
證畢

則由式(4)，式(5)和式(6)可知：

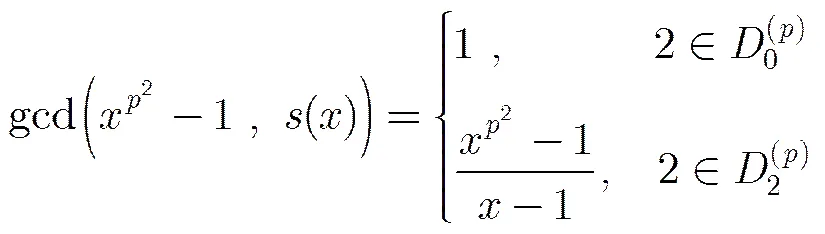
因此，

證畢

4 結論

[1] Golomb S W and Gong G. Signal Design for Good Correlation: For Wireless Communication, Cryptography and Radar Applications[M]. Cambridge: UK, Cambridge University Press, 2005: 174-175.

[2] Massey J L. Shift register synthesis and BCH decoding[J]., 1969, 15(1): 122-127.

Du Xiao-ni, Yan Tong-jiang, and Shi Yong-fang. Linear complexity of generalized cyclotomic sequences with periodp[J].&, 2010, 32(4): 821-824.

[4] Du Xiao-ni and Chen Zhi-xun. Trace representation of binary generalized cyclotomic squences with length p[J].-, 2011, E94-A(2): 761-765.

Li Rui-fang and Ke Pin-hui. The linear complexity of a new class of generalized cyclotomic sequences with period 2[J].&, 2014, 36(3): 650-654.

[6] Chang Zu-ling and Li Dan-dan. On the linear complexity of the quaternary cyclotomic sequences with the period 2[J]., 2014, E97-A(2): 679-684.

[7] Li Xiao-ping, Ma Wen-ping, and Yan Tong-jiang. Linear complexity of binary Whiteman generalized cyclotomic sequences of order 4[J]., 2013, 96A(1): 363-366.

[8] Zhao Chun-e and Ma Wen-ping. Autocorrelation values of generalized cyclotomic sequences of order six[J]., 2013, E96-A(10): 2045-2048.

[9] Edemskiy V and Lvanov A. Linear complexity of quaternary sciences of lengthwith low autocorrelation[J]., 2014, 259B: 555-560.

[10] Ke Pin-hui, Lin Chang-lu, and Zhang Sheng-yuan. Linear complexity of quaternary sciences with odd period and low autocorrelation[J]., 2014, 21(5): 89-93.

[11] Li Dan-dan and Wen Qiao-yan. Linear complexity of generalized cyclotomic quaternary sequences with period[J]., 2014, E97-A(5): 1153-1158.

[12] Yan Tong-jiang and Li Xiao-ping. Some note on the generalized cyclotomic sequence of length 2pand p[J]., 2013, E96-A(10): 997-1000.

[13] Zhang Jing-wei, Zhao Chang-an, and Ma Xiao. Linear complexity of generalized cyclotomic binary sequences with the period 2p[J]., 2010, 21(2): 93-108.

[14] Zhang Jing-wei, Zhao Chang-an, and Ma Xiao. On the linear complexity of generalized cyclotomic binary sequences with length 22[J]., 2010, E93-A(1): 302-308.

[15] Ke Pin-hui and Zhang J. On the linear complexity and autocorrelation of generalized cyclotomic binary sequences with length 2p[J].,, 2013, 67 (3): 325-339.

[16] Cusick T and Ding Cun-sheng. Stream Ciphers and Number Theory[M]. ElsevierScience, 2004: 198-212.

[17] Yan Tong-jiang, Huang Bing-jia, and Xiao Guo-zhen. Cryptographic properties of some binary generalized cyclotomic sequences with length2[J]., 2008, 178(4): 1078-1086.

[18] Ding Cun-sheng and Hellseth. T. New generalized cyclotomy and its applications[J].1998, 4(2): 140-166.

Linear Complexity of Binary Generalized Cyclotomic Sequences of Order Four with Period 2p2

Du Xiao-ni Wang Guo-hui Wei Wan-yin

(,,730070,)

Based on the theory of generalized cyclotomic, a new class of binaey generalized cyclotomic sequences of order four with periodis established. Using the theory of polynomial factor over finite field, the linear complexity and minimal polynomial of the new sequences are researched. Results show that the sequences has larger linear complexity and can resist the attack by B-M algorithm. It is a good sequence from the viewpoint of cryptography.

Stream ciphers; Generalized cyclotomic sequence; Linear complexity; Minimal polynomial

TN918.4

A

1009-5896(2015)10-2490-05

10.11999/JEIT150180

2015-02-02；改回日期：2015-07-01；

2015-07-17

王國輝 wanggh0039@126.com

國家自然科學基金(61202395, 61462077, 61262057, 61562077)和教育部“新世紀優秀人才支持計劃”基金(NCET-12- 0620)

The National Natural Science Foundation of China (61202395, 61462077, 61262057, 61562077); The Program for New Century Excellent Talents in University (NCET-12-0620)

杜小妮： 女，1972年生，教授，研究方向為密碼學與信息安全.

王國輝： 男，1991年生，碩士生，研究方向為密碼學與信息安全.

魏萬銀： 女，1989年生，碩士生，研究方向為密碼學與信息安全.