一種計算旋轉對稱布爾函數的漢明重量和非線性度的新方法

張習勇 祁應紅 高光普 李玉娟

?

一種計算旋轉對稱布爾函數的漢明重量和非線性度的新方法

張習勇①②④祁應紅*①高光普③李玉娟④

①(信息工程大學 鄭州 450002)②(數學工程與先進計算國家重點實驗室 無錫 214215)③(洛陽外國語學校 洛陽 471003)④(信息保障技術重點實驗室 北京 100072)

旋轉對稱布爾函數是一類重要的密碼學函數，研究其重量和非線性度等密碼學性質具有很好的理論價值。區別于已有的計算方法，該文利用特定的正規基把這些布爾函數的問題轉化為有限域上的指數和問題，得到了和時一些二次旋轉對稱布爾函數的重量和非線性度的新結果。使用所提的方法，可以計算幾乎全部的二次旋轉對稱布爾函數的重量和非線性度。所提的新方法對于研究一般的旋轉對稱布爾函數具有一定的參考意義。

密碼學；旋轉對稱布爾函數；非線性度；漢明重量；正規基

1 引言

布爾函數在現代密碼學中有著廣泛的應用，很多學者致力于其性質和應用的研究。1999年，Pieprzyk等人[1]提出了旋轉對稱布爾函數的概念，這類布爾函數在輸入變量旋轉變化時，其函數值保持不變。人們在研究中發現這種類型的布爾函數具有良好的密碼學性質，并將其應用于如MD4, MD5, HAVAL等一些摘要算法中。對這種類型的布爾函數的非線性度和漢明重量的研究取得了很好的結果。例如在2002年，Cusick等人[2]研究了一類二次旋轉對稱布爾函數的快速求值，得到了該類布爾函數的重量，并且給出了當變元個數為偶數時此類函數的非線性度。同時他們通過分析實驗數據，提出了一個猜想：旋轉對稱布爾函數的非線性度和其漢明重量相等。2010年，Ciungu[3]證明了該猜想在變元個數為3的倍數時是成立的，2011年，Zhang等人[4]證明了上述猜想。2012年，Wang等人[5]將此猜想推廣到了次數為4的旋轉對稱布爾函數，證明了的非線性度與其漢明重量相等。

近來，人們分別研究了旋轉對稱布爾函數的非線性度、重量和其它性質，有些結論可用公式直接表示這兩個參數。文獻[11]刻畫了二次單軌道旋轉對稱布爾函數的漢明重量和非線性度，文獻[12]中給出了一類特殊的二次雙軌道旋轉對稱布爾函數的漢明重量和非線性度，這些結果只能計算極少幾類旋轉對稱布爾函數的情況，而對于一般的情況，這兩篇文章中的方法不再適用。本文利用正規基，將布爾函數的問題轉化為有限域上的指數和問題，這種新方法可能更適合研究一般的旋轉對稱布爾函數。

2 預備知識

定義2[13]元旋轉對稱布爾函數可以用形式表示，其中，稱這種表示方法為的簡代數正規型。

由定義3與定義4以及線性函數的性質可知：

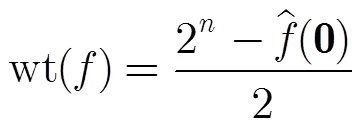
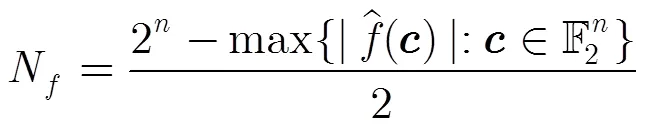
有限域可以看成其子域上的向量空間，針對不同的用途，人們選用不同的向量空間上的基，如正規基，多項式基等。在上的正規基是形式如的一組元素，選用這樣正規基的優點之一是做平方運算不費計算資源(可以忽略不計)。由正規基定理知，對任意的，在中存在一組上的正規基。假設正規元為，則對任意的，存在使得，稱為在此基下的坐標。

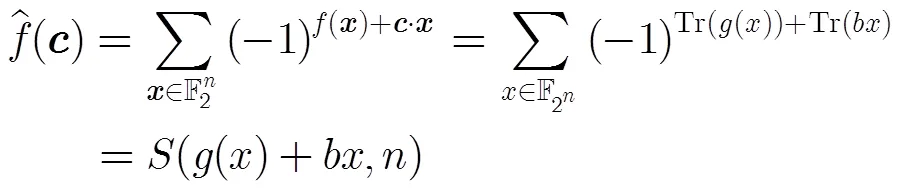
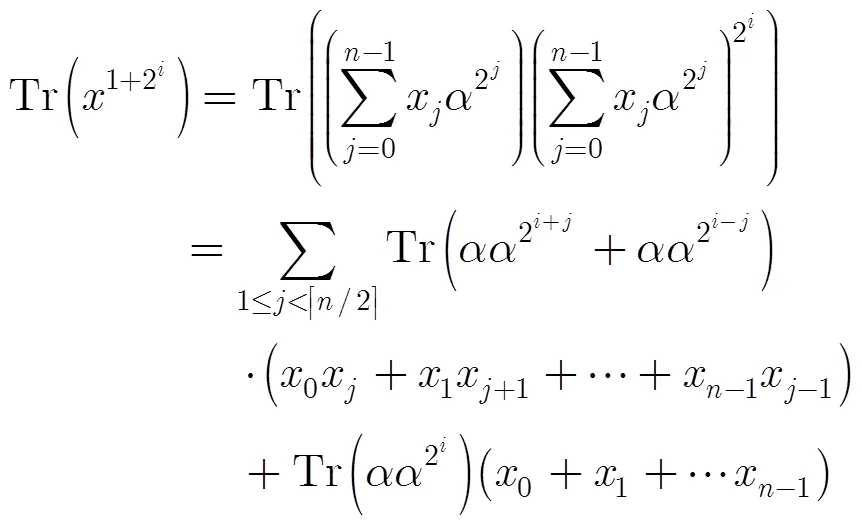
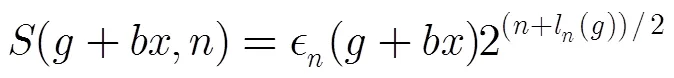
本文需要關于有限域上具有良好跡正交關系的正規基的一些結果，下面的結論另文給出，也可參見文獻[15]。

定理2[14]假設正整數,滿足，奇素數(可相同)滿足則有，其中為雅可比符號。

定理3[14]令,，記為在中的階，令。正整數,滿足,，則

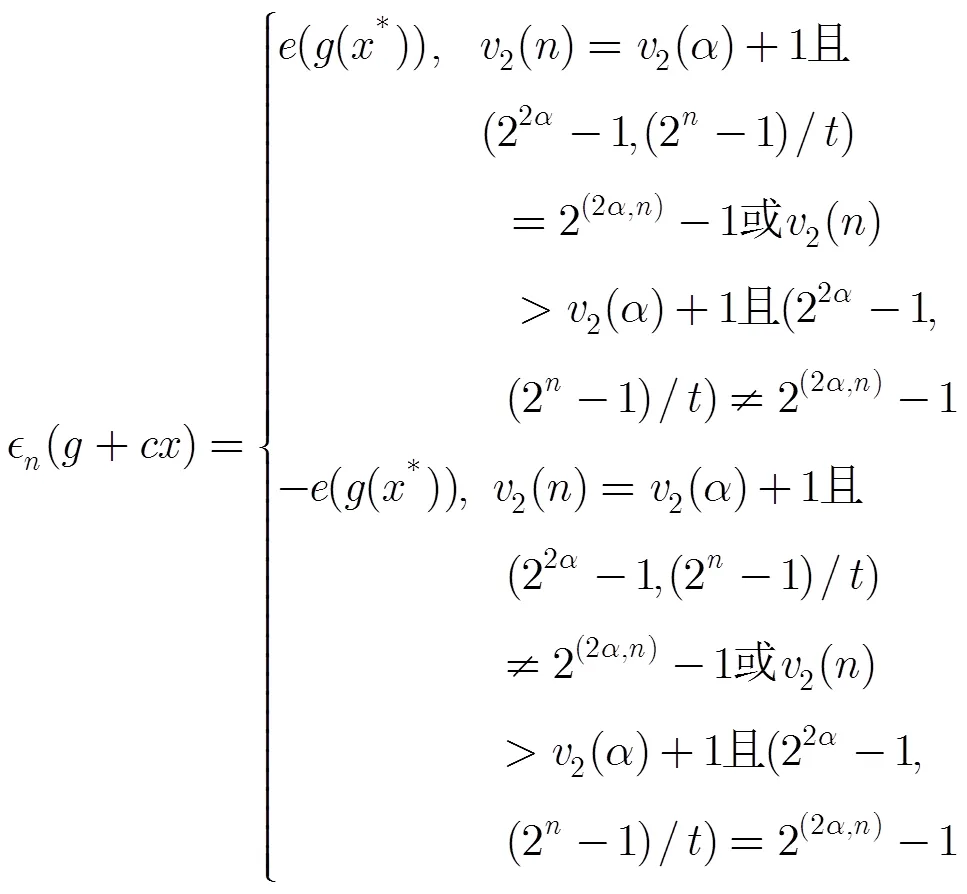
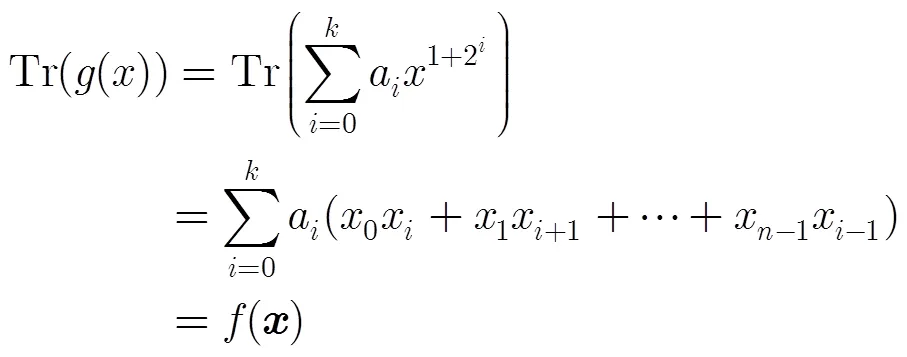
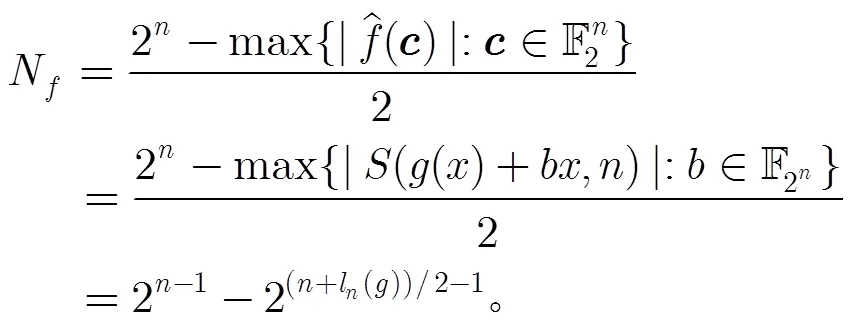
由定理2知

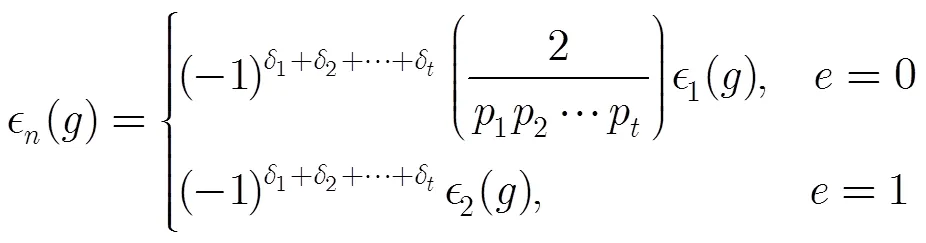
另一方面

從而

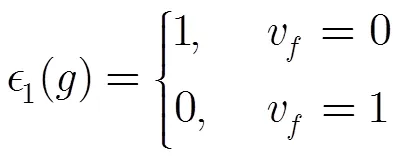
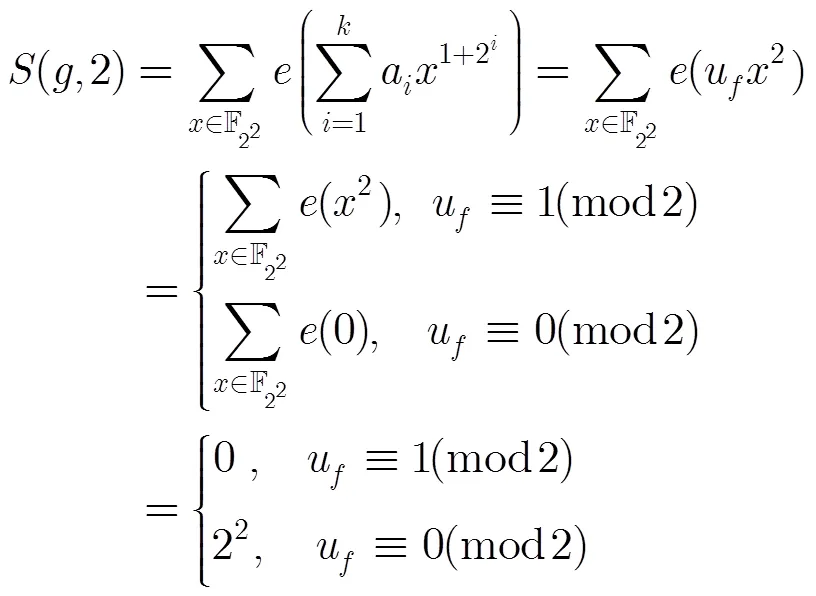
故此時

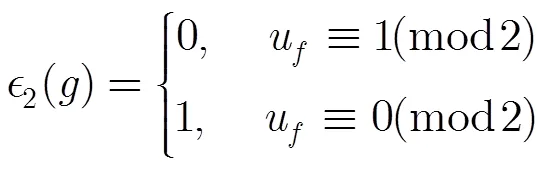
綜上可得

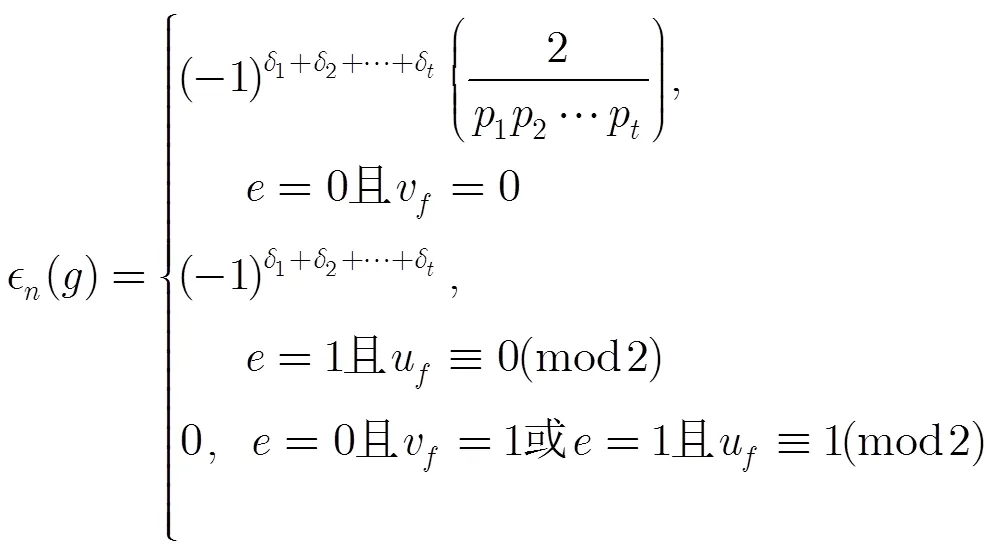
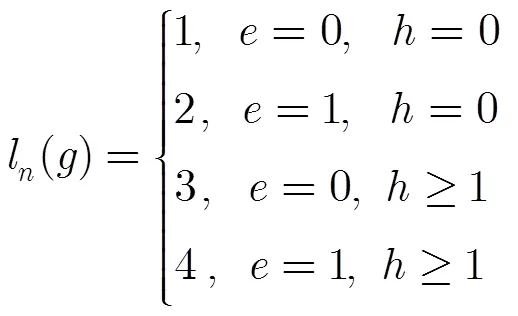
從而可得

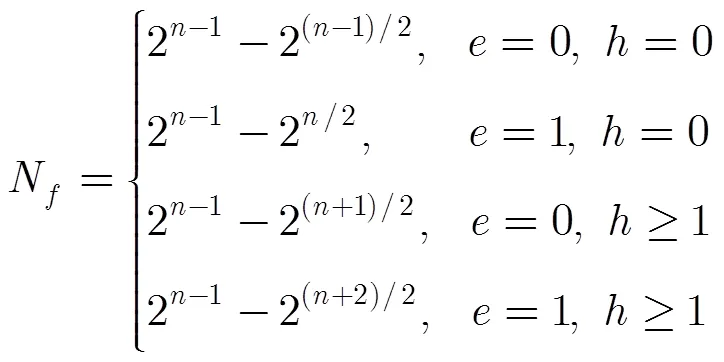
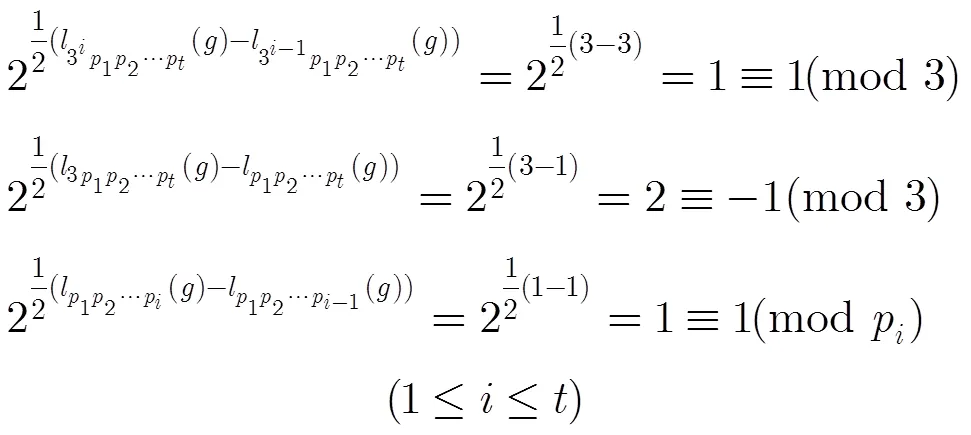
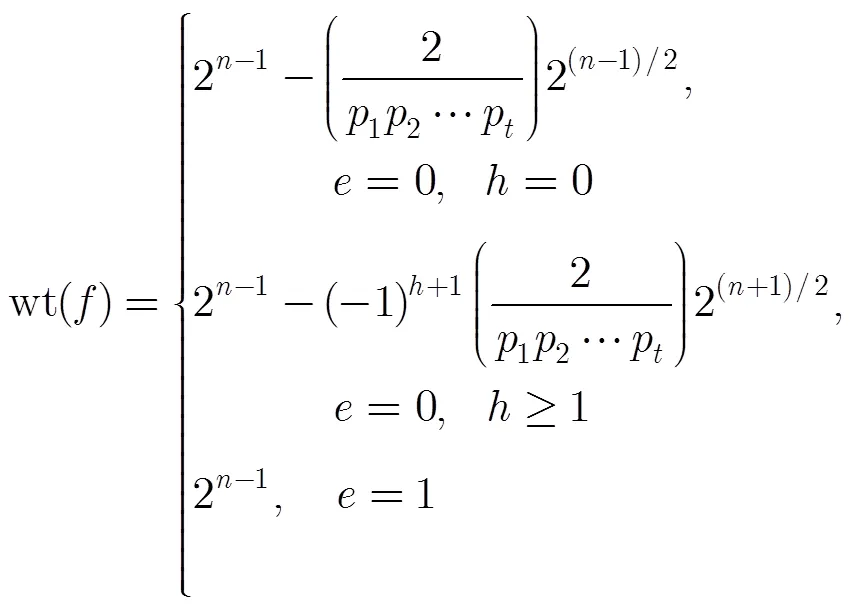
表1是利用計算機編程得到的該函數的漢明重量和非線性度，可用例子中得出的公式進行驗證。沿用定理4中的符號及。當即，且對定理4中給出的,時，該函數的重量和非線性度的計算有更簡單的公式。證明的方法與定理4的證明類似，只需結合文獻[14]中定理5.1，在此只給出結論。

表1計算機編程得到的例1的部分結果

910111314151718 224480992403280641612865280130048 2885121056416081921664065280131072

表2計算機編程得到的例2的部分結果

1014182226 4808064130560209510433546240

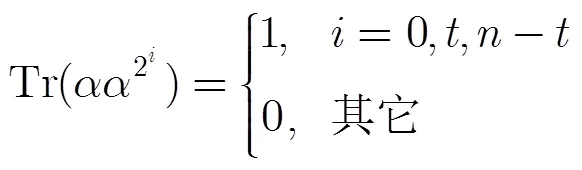
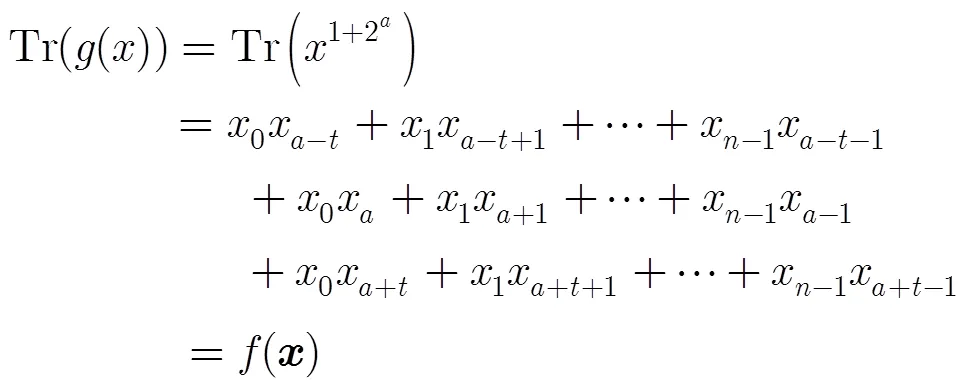
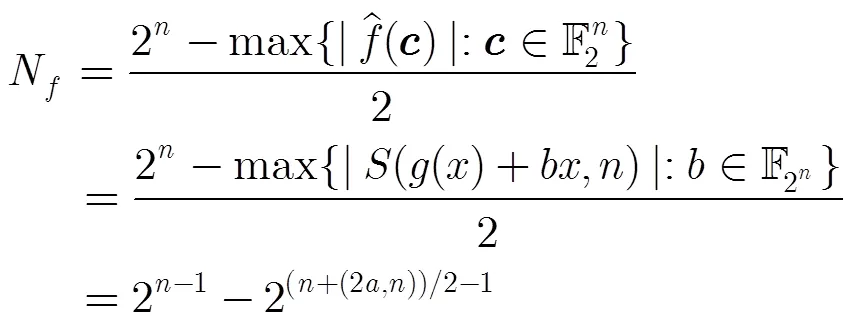
證畢

5 與已有結論及方法的比較

目前對于二次旋轉對稱布爾函數的重量和非線性度的研究結果有限，原因之一是沒有一般性的辦法來解決這類二次函數的指數和的計算問題，如上述兩文中的方法只能適用于上述兩文中的特殊的二次旋轉對稱布爾函數。本文使用的方法與上述兩個文獻中使用的方法不同，將二次旋轉對稱布爾函數的重量和非線性度的問題轉化為有限域上單變元函數的指數和計算問題，最終求取了時任意的二次旋轉對稱布爾函數的重量和非線性度，同時對時的特殊類型的旋轉對稱布爾函數重量和非線性度進行了刻畫。當時，文獻[11]的結論是本文定理4的特殊情形，而文獻[12]的結論是本文例1的特殊情形。相比于已有的方法，本文的這種利用特殊的正規基的方法更有一般性，能計算大部分二次旋轉對稱布爾函數的非線性度，且計算非線性度時，主要運算之一是求取特殊的具有指定正交關系的正規基(參見文獻[16]等，可知有時(如)是線性運算)。本文方法對研究一般的高次旋轉對稱布爾函數也有一定的參考意義。

[1] Pieprzyk J and Qu C X. Fast hashing and rotation-symmetric functions[J]., 1999, 5(1): 20-31.

[3] Ciungu L C. Cryptographic Boolean functions: Thus-Morse sequences, weight and nonlinearity[D]. [Ph.D. dissertation], University at Buffalo, 2010.

[4] Zhang X, Guo H, Feng R,.. Proof of a conjecture about rotation symmetric functions[J]., 2011, 311(14): 1281-1289.

[5] Wang B, Zhang X, and Chen W. The hamming weight and nonlinearity of a type of rotation symmetric Boolean function [J].,, 2012, 55(4): 613-626.

[6] Cusick T W. Finding Hamming weights without looking at truth tables[J]., 2013, 5(1): 7-18.

[7] Brown A and Cusick T W. Equivalence classes for cubic rotation symmetric functions[J]., 2013, 5(2): 85-118.

[8] KV L, Sethumadhavan M, and Cusick T W. Counting rotation symmetric functions using Polya’s theorem[J]., 2014, 169: 162-167.

[9] Cusick T W and Cheon Y. Affine equivalence for cubic rotation symmetric Boolean functions with=variables[J]., 2014, 327: 51-61.

[10] Cusick T W and Cheon Y. Affine equivalence of quartic homogeneous rotation symmetric Boolean functions[J]., 2014, 259: 192-211.

[11] Kim H, Park S M, and Hahn S G. On the weight and nonlinearity of homogeneous rotation symmetric Boolean functions of degree 2[J]., 2009, 157(2): 428-432.

[12] Liu H. On the weight and nonlinearity of quadratic rotation symmetric function with two MRS functions[J]., 2013, 16(1): 12-19.

[14] Hou X D. Explicit evaluation of certain exponential sums of binary quadratic functions[J]., 2007, 13(4): 843-868.

[15] Weinberger M J and Lempel A. Factorization of symmetric circulant matrices in finite fields[J]., 1990, 28(3): 271-285.

[16] Zhang X, Cao X, and Feng R. A method of evaluation of exponential sum of binary quadratic functions[J]., 2012, 18(6): 1089-1103.

A New Method for Evaluation of Hamming Weight and Nonlinearity of Rotation-symmetric Boolean Functions

Zhang Xi-yong①②④Qi Ying-hong①Gao Guang-pu③Li Yu-juan④

①(,450002,)②(,214215,)③(,471003,)④(,100072,)

Rotation-symmetric Boolean function is a class of Boolean functions with good cryptographic properties, and researches on its weight and nonlinearity cryptographic properties have good theoretical value. Different from the conventional calculation method, in this paper, these problems are converted to the evaluation of exponential sum on finite fields with a specific normal basis. Some new results about the weight and nonlinearity of some rotation-symmetric Boolean functions of degree 2 withandare obtained. Using the proposed method, the weight and nonlinearity of almost all Rotation-symmetric Boolean functions of degree 2 can be evaluated. This new method is also interesting for studies on the other Boolean functions.

Cryptography; Rotation-symmetric Boolean functions; Nonlinearity; Hamming weight; Normal bases

TN918

A

1009-5896(2015)11-2691-06

10.11999/JEIT 150164

2015-01-29；改回日期：2015-06-11；

2015-07-27

祁應紅 yinghong_qi@163.com

國家自然科學基金(61402522, 60803154, 61572027)；數學工程與先進計算國家重點實驗室課題；信息保障技術重點實驗室開放基金(KJ-13-108)

The National Natural Science Foundation of China (61402522, 60803154, 61572027); Project of State Key Lab of Mathematical Engineering and Advanced Computing; Open Foundation of Science and Technology on Information Assurance Laboratory (KJ-13-108)

張習勇：男，1975年生，副教授，研究方向為編碼密碼學.

祁應紅：男，1986年生，碩士生，研究方向為編碼密碼學.

高光普：男，1984年生，講師，研究方向為對稱密碼設計與分析.