一種基于保角相位的圖像邊緣檢測新方法

石美紅 李 青 趙雪青 喬冬冬

?

一種基于保角相位的圖像邊緣檢測新方法

石美紅*李 青 趙雪青 喬冬冬

(西安工程大學計算機科學學院 西安 710048)

為了提高邊緣檢測精確度與抗噪性能，該文提出一種基于保角相位的圖像邊緣檢測新方法。該方法首先利用保角單演信號能夠表達不同本征維數的圖像局部結構的特點，采用指數函數計算相位偏差，有效地抑制了相位一致模型邊緣檢測中產生的偽邊緣和噪聲，提高了邊緣檢測的精確度；其次，利用Poisson核在空域中有解析表示的優勢，降低了算法復雜度。仿真實驗結果表明，與現有的相位一致性圖像邊緣檢測方法相比，該方法提取的圖像邊緣更精確、更完整、更均勻，對噪聲具有更好的魯棒性，同時，計算復雜度較低。

圖像處理；邊緣檢測；相位一致性；保角單演信號；本征維數

1 引言

邊緣檢測一直是計算機視覺領域中極具挑戰性的研究課題之一，也是圖像分析與模式識別的重要環節之一。研究表明人類對物體的感知在很大程度上依賴于邊緣[1]。常見的邊緣有脈沖型、階躍型、斜坡型、屋脊型。目前，用于圖像邊緣檢測的算法有很多，最經典且具代表性的有Sobel算子、Prewitt算子、Laplace算子和Canny算子等，因算法簡單、可行而被廣泛運用。但是，這些算子都是采用微分算法，對圖像的光照和對比度變化比較敏感。由于邊緣和噪聲同屬于高頻分量，從而也影響了抗噪性能，限制了其在實際中的使用。盡管人們也研究了其他改進和優化的邊緣檢測方法，諸如，文獻[2]提出先用ADM空域算子計算初始邊緣圖，再利用改進的極大值抑制算法得出最佳邊緣檢測結果，與傳統算法相比，該算法的檢測抗噪性能更佳；文獻[3]提出利用自回歸模型和2維最大條件熵對Canny邊緣檢測算法改進，能夠自動選取邊緣檢測的閾值參數，并對3種噪聲的抑制效果較好；文獻[4]提出了分布式的Canny算子計算方法，解決了Canny算子復雜度較高的問題。但是，這些改進的算法核心仍然是基于微分計算，所以，仍然存在著上述的問題。

基于相位一致性(Phase Congruency, PC)的圖像邊緣檢測方法是用圖像中傅里葉分量相位的一致點檢測邊緣，可使得各類型的邊緣特征都在相位一致性高的點出現，且具有對光照和對比度變化不敏感的優勢[5,6]。為了進一步提高邊緣檢測性能，文獻[7]改進了相位一致性的計算模型，使得提取的邊緣精確度和抗噪性能有了改善，也使其得到廣泛應用。文獻[8]在相位一致性圖像上計算分形維數作為圖像質量評估的特征；文獻[9]提出基于相位一致性的局部描述符用于識別人臉面部表情；文獻[10]利用相位一致性對影像紋理描述穩定的特點, 提出了一種基于相位一致性的尺度不變特征變換的多源遙感影像自動配準方法。但是，采用文獻[7]方法易于產生偽邊緣和噪聲，且計算復雜。因此，文獻[11]提出將單演信號相位一致性(Monogenic Phase Congruency, MPC)模型用于圖像特征檢測的方法，有效地提高了邊緣檢測精確度，降低了計算復雜度，但是，單演信號對圖像局部結構的表征能力有限，使其所提取的邊緣易出現丟失或不連續的現象。受文獻[12]的啟示，本文利用保角單演信號能夠表達不同本征維數的圖像局部結構的特點，通過改進相位一致性計算模型，提出了一種基于保角單演相位一致性(Conformal Monogenic Phase Congruency, CMPC)的圖像邊緣檢測新方法，與Canny梯度和改進的PC方法相比，用本文方法所提取的圖像邊緣更精確、更完整、更均勻，并具有較好的抗噪性能和較低的計算復雜度。

2 相位一致性

相位一致性的實質就是圖像的各個頻率成分的相位相似性的一種度量方式[6]，其定義為

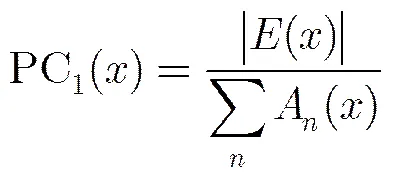
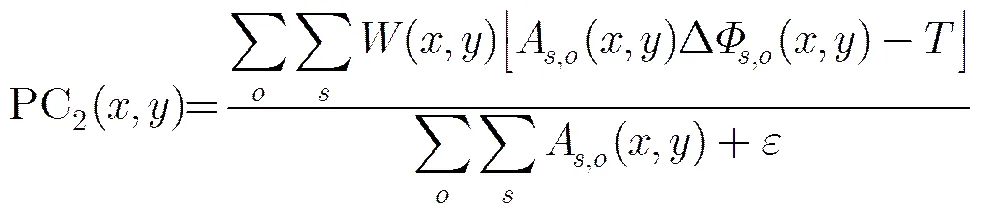
式中

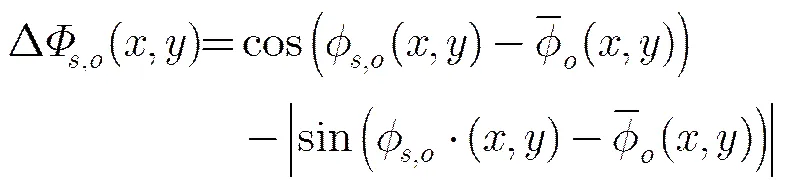
由于文獻[7]的算法復雜度較高，為此，文獻[11]提出用MPC模型檢測圖像特征的方法。單演信號是采用Riesz變換取代Hilbert變換，將1維解析信號各向同性推廣至2維[13]。MPC的計算模型為

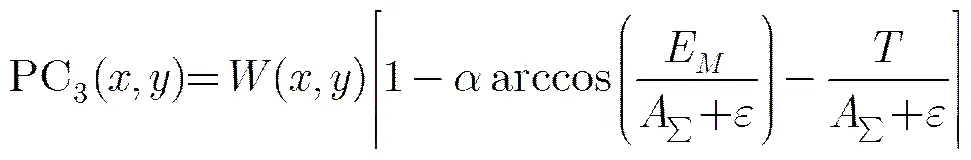
在MPC模型中，計算局部能量時，減少了方向采樣；計算相位偏差時，直接使用反余弦函數，相對于式(2)，算法更簡便。但是，用單演信號相位一致模型會導致檢測的邊緣出現部分丟失或不連續。

3 基于角相位的邊緣檢測方法

3.1 CMPC算法

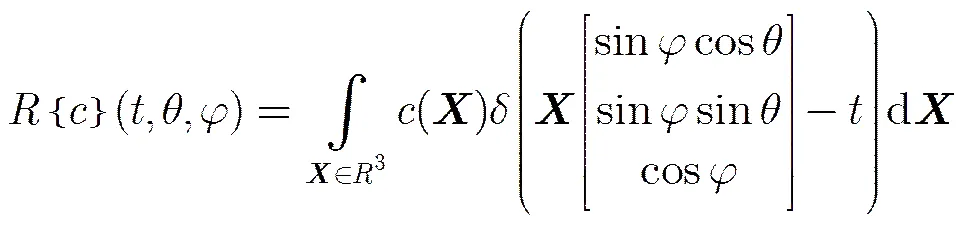
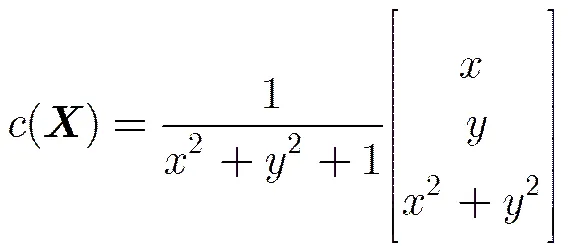
類似于單演信號，保角單演信號定義為

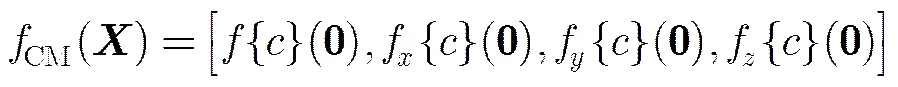
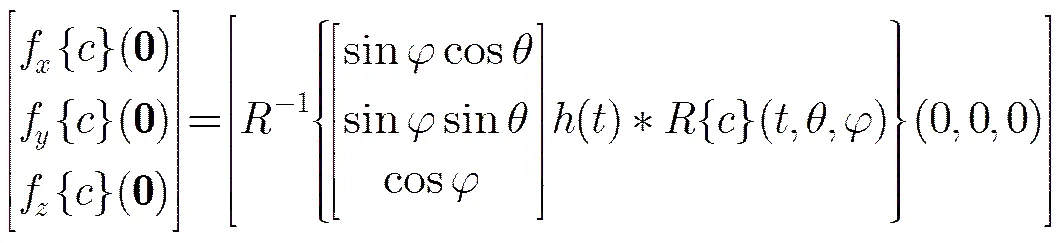
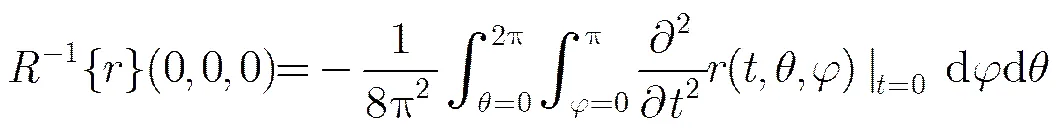
在計算CMPC時，由于Log-Gabor 濾波器沒有空域的解析表示，無法將尺度空間向高維信息空間映射，所以選用了DOP(Difference Of Possion)濾波器[16]。DOP是由兩個Poisson核組成帶通濾波器。Poisson核和Riesz變換核兩者非常相似，由Poisson核可以推導建立單演尺度空間[17]，可有機地將解析信號與尺度空間聯系起來，所以，Poisson核在計算單演信號時具有先天性的優勢。DOP濾波器的表達式為

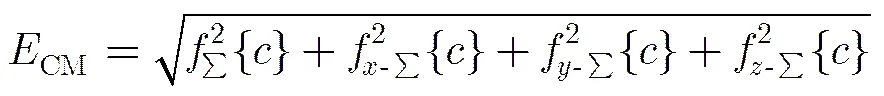
式中

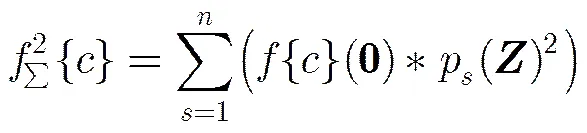
基于保角單演信號的相位一致性計算模型為

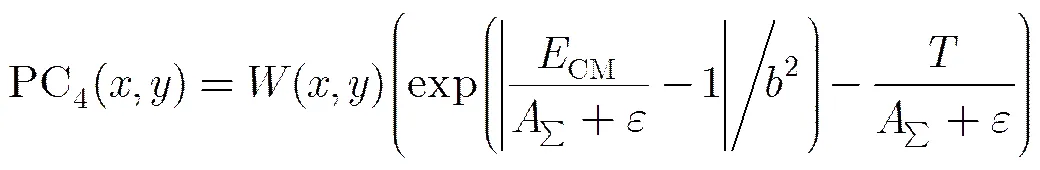
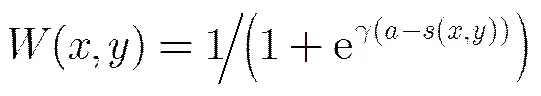
為了降低噪聲的影響，選用瑞利分布模型評估噪聲能量[18]，其定義為

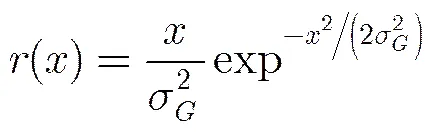
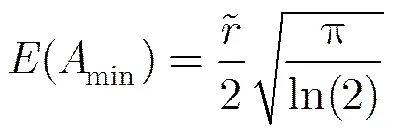
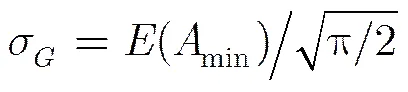
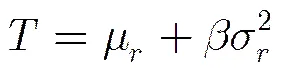
CMPC算法的具體流程如下：

3.2 參數選取

4 實驗結果分析及其性能對比

實驗在i3-2328處理器、主頻2.2 GHz、內存2 GB和MALTAB 2008a平臺上進行，分別與Canny梯度、文獻[7]、MPC等方法進行實驗對比。各方法的參數選取以最佳效果為準：文獻[7]方法的尺度參數=3，方向參數=6，最小波長為3，濾波器兩個相鄰的尺度比例為2; MPC方法的尺度參數=4,=1.5，其他參數與文獻[7]方法一致；CMPC方法的尺度參數=3。

圖1 不同尺度參數s下CMPC的邊緣檢測結果圖

4.1 不同算法的邊緣檢測實驗結果分析

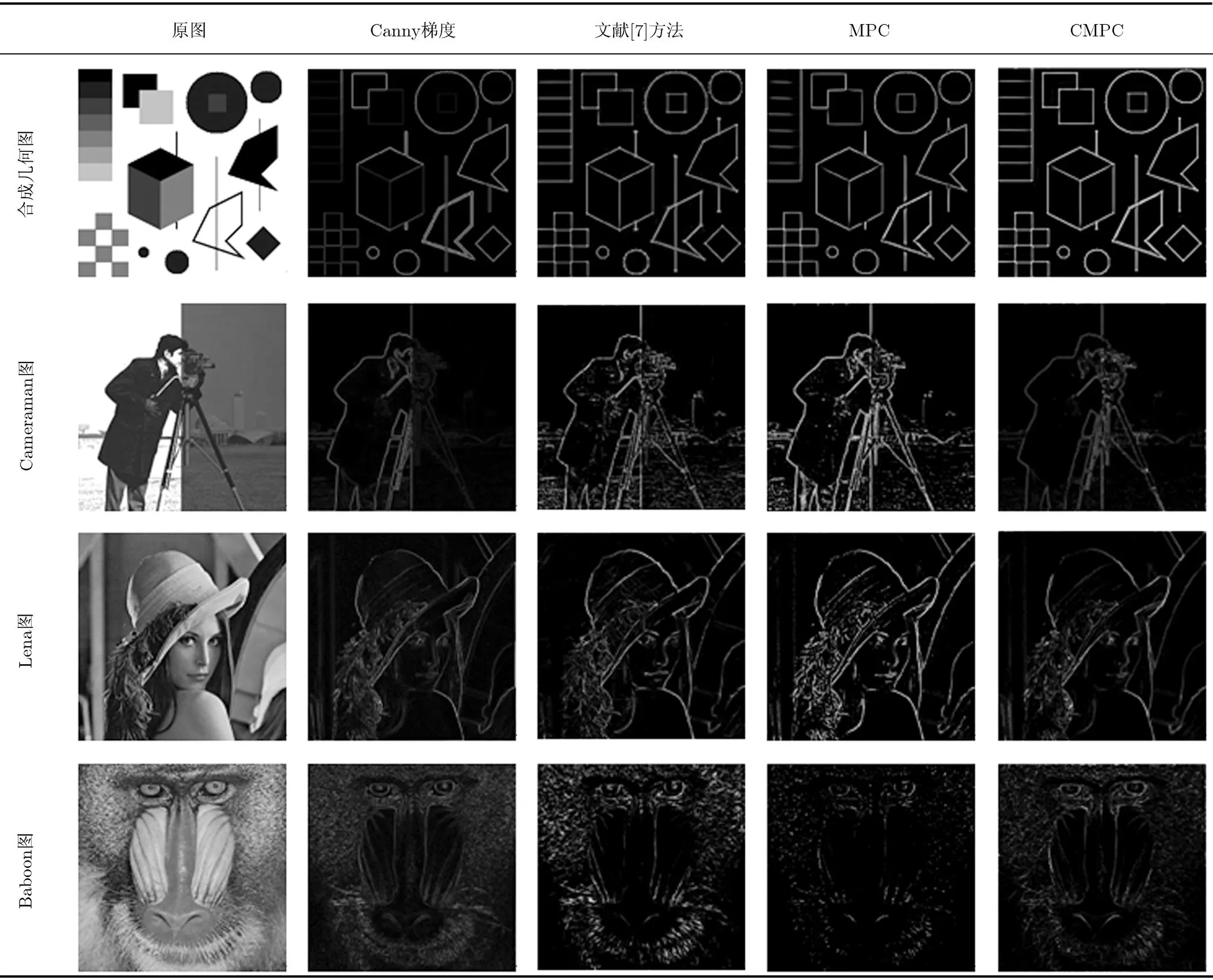
表1給出了不同方法的實驗結果圖。原始圖的大小為256×256。為了進一步驗證相位一致性對光照變化的不敏感性，對Cameraman圖進行了人工處理，即增加左半圖的亮度，降低右半圖的亮度。由表1的邊緣檢測結果看，用Canny梯度檢測的邊緣會出現許多偽邊緣信息，如合成幾何圖右下方的多邊形；Lena圖的臉頰和肩膀處的平滑區域；Baboon圖的面額、鼻子和胡須等，同時，由Cameraman圖的檢測結果不難看出，用Canny梯度提取的邊緣易受到光照強度變化的影響，諸如，左半圖提取的邊緣強度明顯大于右半圖，而用相位一致性方法檢測的邊緣不受光照強度變化的影響，其邊緣強度均勻，產生的偽邊緣或噪聲少，這是因為Canny梯度對圖像的對比度變化比較敏感，所以，微小的灰度變化點都會被誤檢為邊緣點。在相位一致性的檢測方法中，由合成幾何圖的檢測結果不難看出，文獻[7]方法提取的邊緣會不同程度地出現“毛刺”，如圖中的圓和垂直線兩端，MPC方法提取的邊緣會不同程度地出現丟失，如位于圖中左上方一系列的灰度漸變矩形的邊緣和中間正方體棱角的連接處，相對而言，CMPC方法提取的邊緣更完整、更均勻；從其他圖的檢測結果看，用文獻[7]方法和MPC方法檢測會不同程度地出現偽邊緣或因邊緣丟失導致不連續的邊緣點，如Cameraman的衣袖和褲子的皺褶，Lena的帽身和背景物的邊緣，Baboon的面額皺褶、外鼻輪廓和胡須等，相對而言，用CMPC方法檢測的邊緣更精確、更完整、更均勻，這是因為CMPC方法能更好地表達圖像結構的特征，可提高邊緣檢測的精確度，同時，采用指數函數計算相位偏差，能有效地抑制相位一致模型邊緣檢測中產生的偽邊緣和噪聲信息。

表1不同方法的邊緣檢測結果

4.2 性能對比

4.2.1邊緣檢測的精確度與抗噪性 為了更客觀地評定本方法的邊緣檢測精確度與抗噪性，選用了大小為128×128的vertical圖[19]進行測試。如表2所示，vertical的左半圖灰度值為115，右半圖灰度值為140，兩者之間是灰度值為128的單像素列。然后，在圖中分別添加零均值、標準方差為2.5, 3.6, 5.7, 8.0, 18.0, 25.0的高斯白噪聲，對應的信噪比分別為100, 50, 20, 10, 5, 1，如表2的第1列。表2的第2, 3, 4列分別是采用文獻[7]方法、MPC方法和CMPC方法的邊緣檢測結果。從主觀視覺效果看，相對其他方法，CMPC方法檢測的邊緣更完整、更均勻。

表2不同相位一致性方法在vertical圖上的邊緣檢測結果

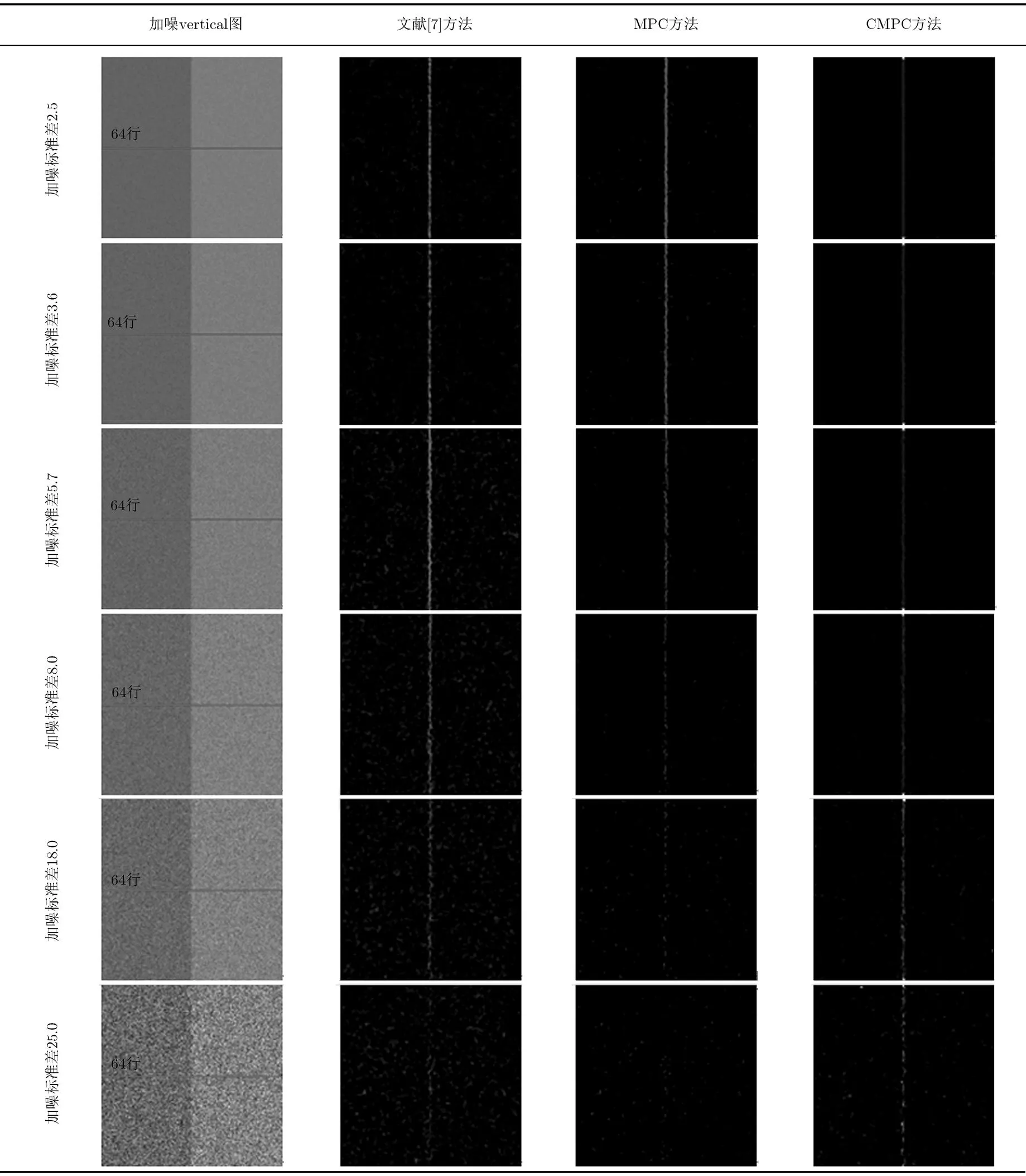
為了更清楚地看出不同方法的邊緣檢測性能，觀測vertical圖中某一行(這里取第64行)的檢測結果，如表3所示。從第64行的原始灰度值的變化情況看，隨著噪聲的增強，不僅左、右半圖間的邊緣信號越來越模糊，而且非邊緣處的噪聲干擾信號也越來越強。從邊緣檢測的結果看，當噪聲較小時(諸如，本圖中標準差低于18.0的加噪圖)，各方法都能精確地檢測出邊緣，但是，隨著噪聲加大，采用文獻[7]方法，在非邊緣處仍有不同程度的噪聲干擾信號，其強度甚至大于邊緣響應信號，采用MPC方法，不僅在非邊緣處存在不同程度的噪聲干擾信號，而且出現邊緣信號丟失的現象。相對而言，采用CMPC方法，當噪聲較小時，在精確地檢測出邊緣的同時，能有效抑制噪聲干擾，隨著噪聲的加大，盡管在非邊緣處也出現了一些噪聲干擾信號，但是其強度遠低于邊緣響應信號。這表明，CMPC方法所檢測出的邊緣不僅精確、穩健，且對噪聲具有較好的魯棒性。

本文采用品質因數指標定量評價抗噪性，其定義式為

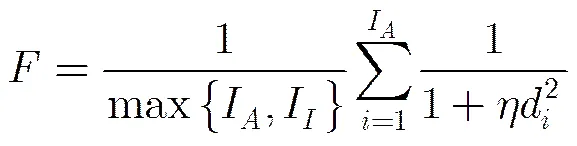
表3 vertical圖原始灰度值和不同方法計算相位一致性值的比較圖

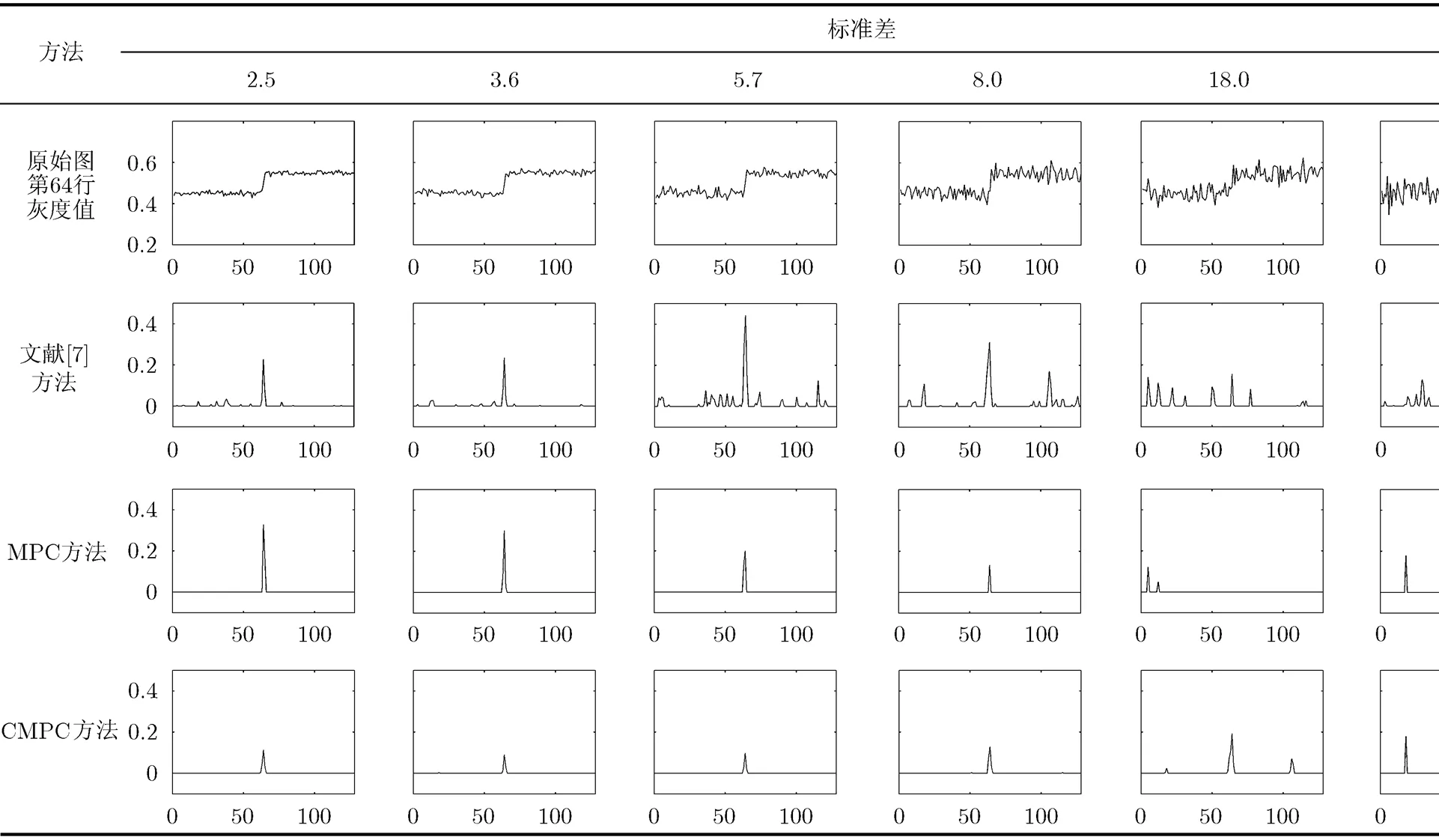
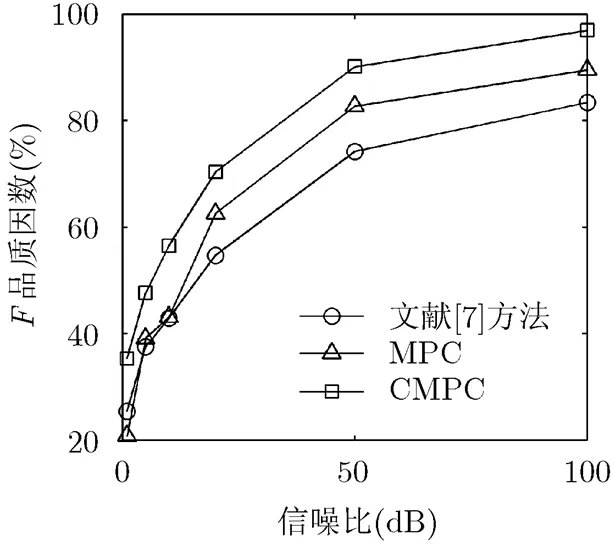
圖2 隨信噪比變化不同方法檢測結果的F品質因數變化曲線圖

4.2.2計算耗時性能 表4給出了不同相位一致性模型用于邊緣檢測的耗時。由表4不難看出，CMPC方法的耗時最小，文獻[7]方法的耗時最大，這是由于文獻[7]方法采用了多尺度、多方向的濾波器計算，而CMPC方法僅用多尺度的濾波器組計算，且將頻域濾波在空域中直接用卷積計算。MPC方法雖然也沒有考慮方向采樣，但是其濾波過程無法用卷積實現，所以，它的時間復雜度居中。

表4不同相位一致計算方法的耗時(s)

方法合成幾何圖Lena圖Cameraman圖Baboon圖 文獻[7]方法0.740.750.820.81 MPC方法0.190.190.210.25 CMPC方法0.100.090.080.09

5 結論

不同于微分圖像特征，相位一致性圖像特征具有對光照變化和噪聲干擾不敏感的優勢。為了提高邊緣檢測精確度和抗噪性能，本文針對已有的相位一致模型邊緣檢測方法存在的不足，提出了一種基于CMPC的邊緣檢測新方法，相對其他相位一致性方法，CMPC方法的主要優勢：(1)提取的邊緣更準確、更完整、更均勻；(2)有效地抑制噪聲干擾；(3)降低了算法復雜度。

[1] Molina C, Baets B, and Bustince H. A framework for edge detection based on relief functions[J]., 2014, 278(10): 127-140.

[2] Ray K. Unsupervised edge detection and noise detection from a single image[J]., 2013, 46(8): 2067-2077.

[3] Hao Fei, Shi Jin-fei, Zhang Zhi-sheng,.. Canny edge detection enhancement by general auto-regression model and bi-dimensional maximum conditional entropy[J]., 2014, 125(15): 3946-3953.

[4] Xu Qian, Varadarajan S, Chakrabarti C,.. A distributed canny edge detector: algorithm and FPGA implementation[J]., 2014, 23(7): 2944-2960.

[5] Morrone M, Ross J, Burr D,.. Mach bands are phase dependent[J]., 1986, 324(6094): 250-253.

[6] Morrone M and Owens R. Feature detection from local energy[J]., 1987, 6(5): 303-313.

[7] Kovesi P. Image features from phase congruency[J]., 1999, 1(3): 1-26.

[8] Liu De-lei, Xu Yong, Quan Yu-hui,.. Reduced reference image quality assessment using regularity of phase congruency[J].:, 2014, 29(8): 844-855.

[9] Shojaeilangari S, Yau W, and Teoh E. A novel phase congruency based descriptor for dynamic facial expression analysis[J]., 2014, 49(11): 55-61.

[10] 李明, 李德仁, 范登科, 等. 利用PC-SIFT的多源光學衛星影像自動配準方法[J]. 武漢大學學報.(信息科學版), 2015, 40(1): 64-70.

Li Ming, Li De-ren, Fan Deng-ke,.. An automatic PC-SIFT-based registration of multi-source images from optical satellites[J]., 2015, 40(1): 64-70.

[11] Wang Li-juan, Zhang Chang-sheng, Liu Zi-yu,.. Image feature detection based on phase congruency by Monogenic filters[C]. The 26th Chinese Control and Decision Conference, Changsha, 2014: 2033-2038.

[12] Fleischmann O, Wietzke L, and Sommer G. Image analysis by conformal embedding[J]., 2011, 40(3): 305-325.

[13] Felsberg M and Sommer G. The monogenic signal[J]., 2001, 49(12): 3136-3144.

[14] Wietzke L, Sommer G, Schmaltz C,.. Differential geometry of monogenic signal representations[C]. Robot Vision: Second International Workshop, Auckland, 2008: 454-465.

[15] Wietzke L and Sommer G. The conformal monogenic signal[C]. Pattern Recognition: 30th DAGM Symposium, Munich, 2008: 527-536.

[16] Felsberg M. Low level image processing with the structure multivector[D]. [Ph.D. dissertation], Christian-Albert Kiel University, 2002: 95-100.

[17] Felsberg M and Sommer G. The monogenic scale-space: a unifying approach to phase-based image processing in scale-space[J]., 2004, 21(1/2): 5-26.

[18] Kovesi P. Phase preserving denoising of images[C]. The Australian Pattern Recognition Society Conference, Perth, 1999: 212-217.

[19] 羅丁, 趙榮椿, 慈林林, 等. 基于Hilbert濾波器對的相位一致性邊緣檢測方法[J]. 中國圖象圖形學報, 2004, 9(2): 139-145.

Luo Ding, Zhao Rong-chun, Ci Lin-lin,.. Phase congruency based edge detection by Hilbert filters[J]., 2004, 9(2): 139-245.

A New Approach for Image Edge Detection Based on Conformal Phase

Shi Mei-hong Li Qing Zhao Xue-qing Qiao Dong-dong

(,’,710048,)

To improve the image edge detection accuracy and anti-noise performance, a new approach for image edge detection based on conformal phase is proposed. Firstly, the proposed approach can effectively improve the precision of edge detection and restrain the false edge and noise by using respectively the conformal monogenic signal which could express local structure of the image with different intrinsic dimensions and an exponential function to calculate the phase deviation. Secondly, it can reduce the complexity of the algorithm by taking advantage of the Poisson kernel of existence of analytic representation in spatial domain. To demonstrate the advantages, the proposed approach is compared with the existing methods of phase congruency based edge detection. The simulation experiment results show that the proposed approach can extract image edge more accurately, more completely, and more uniformly, with better robustness to noise and lower computational complexity.

Image processing; Edge detection; Phase congruency; Conformal monogenic signal; Intrinsic dimensionality

TN911.73

A

1009-5896(2015)11-2594-07

10.11999/JEIT150364

2015-03-27；改回日期：2015-06-29；

2015-08-27

石美紅 meihong_shi@163.com

國家科技支撐計劃基金(2014BAF07B01)；中國紡織工業聯合會科技項目(2014066)

The National Science & Technology Support Program of China (2014BAF07B01); The China National Textile and Apparel Council Science & Technology Program (2014066)

石美紅： 女，1956年生，教授，研究方向為智能信息處理、模式識別等.

李 青： 男，1989年生，碩士生，研究方向為圖像處理與模式識別.

趙雪青： 女，1985年生，博士，講師，研究方向為圖像處理.