非自治動力系統拓撲壓變分原理的一點注記
楊將,郭亞曉
(西北大學數學學院,陜西 西安 710127)
非自治動力系統拓撲壓變分原理的一點注記
楊將,郭亞曉
(西北大學數學學院,陜西 西安710127)
用類似于非自治熵的變分原理的方法,證明了非自治拓撲壓的變分原理的一個不等式,推廣了非自治熵的變分原理,豐富了非自治變分原理的內容.
非自治熵;非自治拓撲壓;變分原理
1 引言
熵是迄今為止發現的重要的非負不變量,每個緊系統都有一個確定的拓撲熵,它被認為是連續作用在底空間上引起混亂程度的一種度量,而估計和計算緊致系統的拓撲熵就成了動力系統的一個永恒的課題.熵分為測度熵和拓撲熵,因此連接測度熵和拓撲熵的變分原理就顯得非常重要.拓撲壓是動力系統中拓撲熵的一種推廣,也是熱力學中的一個重要概念,在熱力學的研究中有著重要的意義.因此,壓的變分原理無論是在動力系統還是在熱力學中都是關注的重點.動力系統又分為自治與非自治,自從自治的熵的變分原理與壓的變分原理被證明以后,對變分原理的研究轉移到更為廣泛的非自治系統的變分原理.2012年朱玉俊在文獻[1]中得到了底空間是緊的、映射序列是連續的且保持Borel測度不變的情況下的非自治熵的變分原理,即
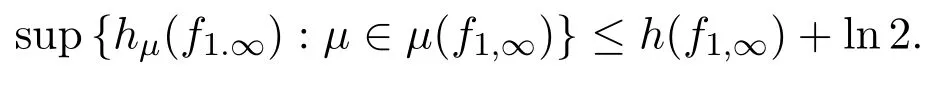
2013年,Jose S.Cánovas在文獻[2]中作了進一步的改進,得到了底空間是距離空間且在有限球維數的情況下去掉ln2的變分原理,即
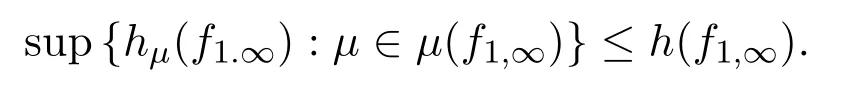
同年Kawan在文獻[3]中給出在映射序列等度連續的情況下非自治熵的變分原理的不等式,即測度熵不超過拓撲熵.受這些文章的啟發,本文把自治拓撲熵的變分原理進一步推廣到非自治拓撲壓的變分原理上,并給出一類非自治動力系統拓撲壓的變分原理不等式.
2 預備知識
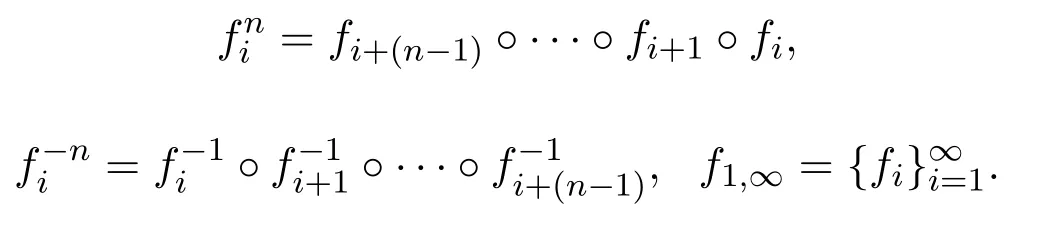
記(X,f1,∞)為非自治動力系統.對于任意的n∈N+,在X上定義新的度量
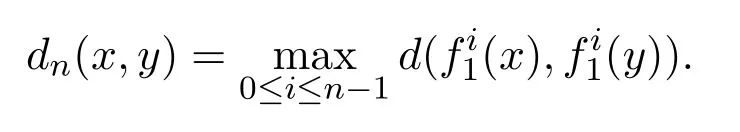
定義2.1[1]設K是X上的緊子集,對任意的ε>0,稱E?X為K的(f1,∞,n,ε)生成集,如果對任意的x∈K,存在y∈E,使得dn(x,y)≤ε.
記r(f1,∞,n,ε,K)為K的(f1,∞,n,ε)生成集的最小基數.
定義2.2[2]設K是X上的緊子集,稱F?K為(f1,∞,n,ε)分離集,如果x,y∈F,xy,則有dn(x,y)>ε.
同樣,記s(f1,∞,n,ε,K)為K的(f1,∞,n,ε)分離集的最大基數.
定義2.3[4]設(X,f1,∞)是非自治動力系統,K是X上的緊子集,定義
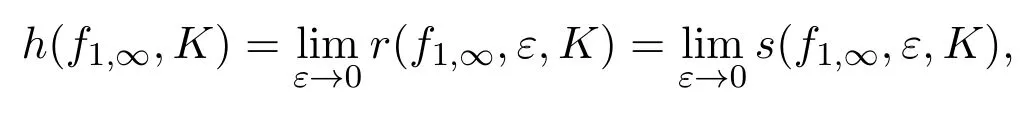
這里
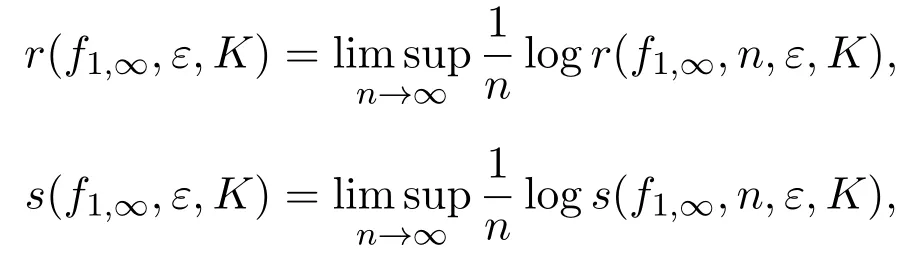
f1,∞的拓撲熵定義為:

有時為了強調度量,記f1,∞的拓撲熵為hd(f1,∞).
設(X,B(X),m)是概率空間,其中B(X)是Borel可測集的全體,為保測變換,即任意的i∈N+,
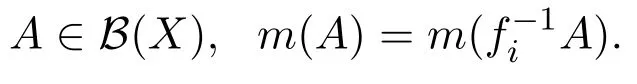
如果對所有的fi,i∈N+,fi保持相同的概率測度m,則稱f1,∞保持m,或m是f1,∞的不變測度,并且記X上的所有保持f1,∞測度不變的全體集合為M(X,f1,∞),現在給出(X,f1,∞)的測度熵的定義.
定義2.4[4]設(X,B(X),m)是概率空間,m∈M(X,f1,∞),ξ是X的一個有限可測分解,定義f1,∞相對于ξ的測度熵為:

定義2.5[5]對任意ε>0,n≥1,φ∈C(X,R),記

3 主要結果及其證明
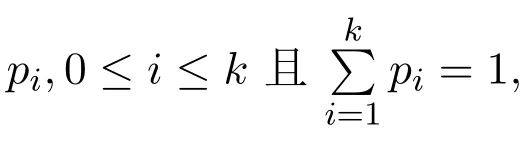
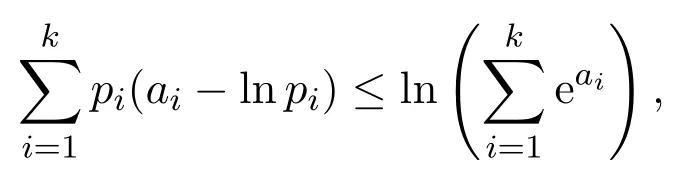
等號成立的充分必要條件為:
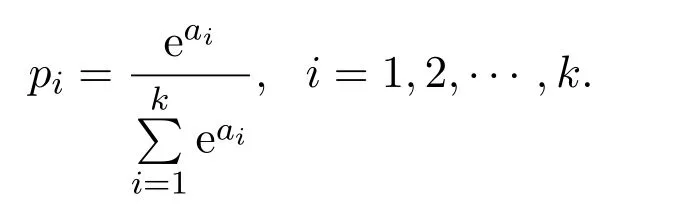
定理3.1設X是緊的度量空間,f1,∞是X上的連續自映射序列,則對任意μ∈M(X,f1,∞),φ∈C(X,R),有
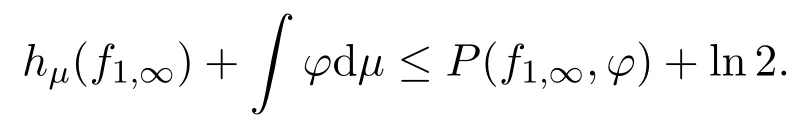


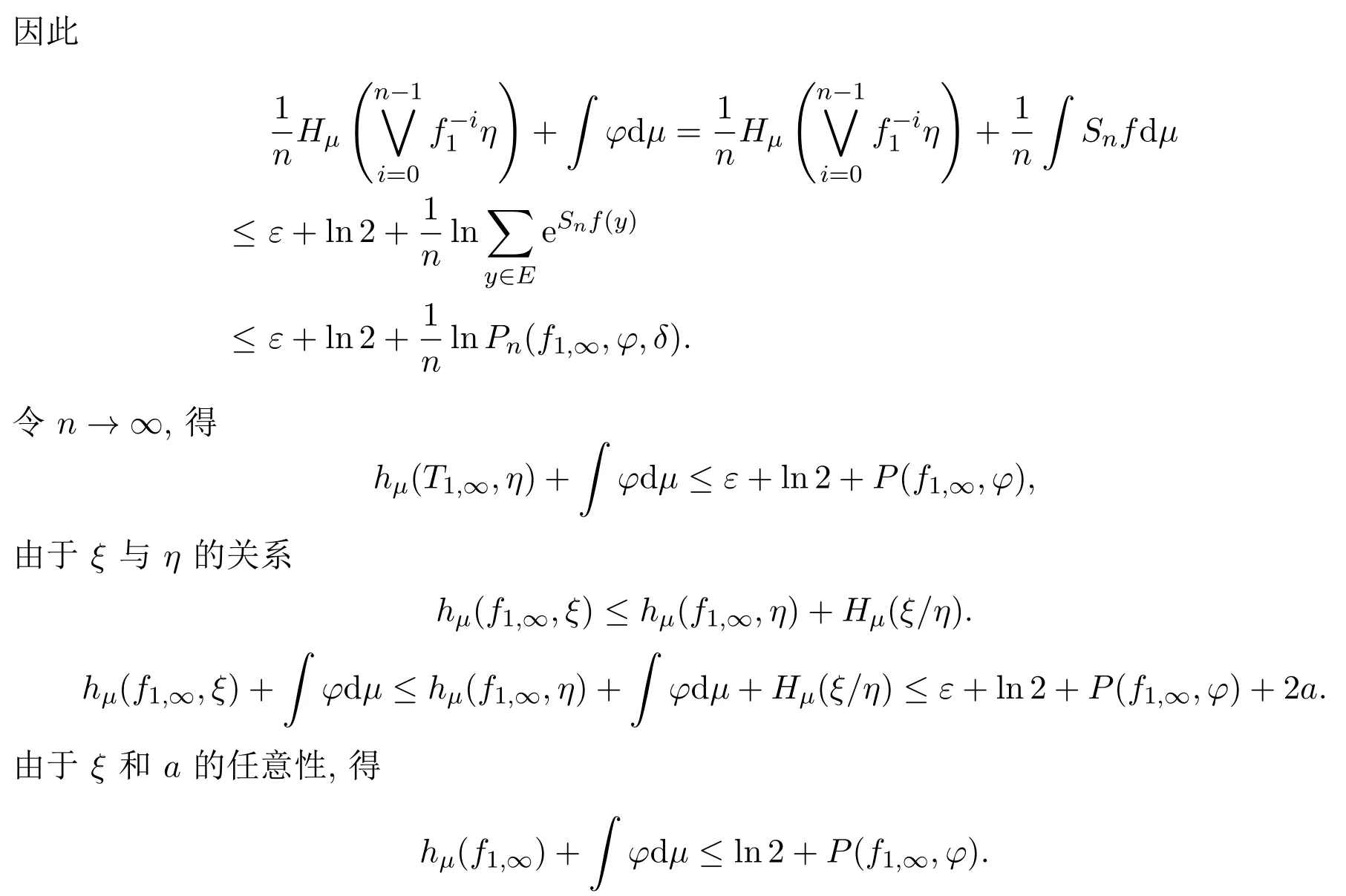
4 問題
在自治熵的變分原理中,Power Rule公式 (即 h(fk)=kh(f))極大的化簡了熵的變分原理的證明過程,使得熵的變分原理的證明被更多的人接受.因此,在非自治的情況下,找到Power Rule公式成為解決非自治變分原理的重要環節.類似于熵的變分原理,壓的變分原理也有P(fk,Skφ)=kP(f,φ),在壓的變分原理證明中的作用類似于自治變分原理的Power Rule公式,遺憾的是在非自治的情況下是不成立的,文獻[7]中給出了反例,正因為這樣,無論是非自治熵的變分原理還是非自治壓的變分原理,都沒有給出變分原理成立的充分必要條件.在此提出兩個問題:
(2)是否可以改進定理3.1的證明給出非自治拓撲壓變分原理成立的充分必要條件.
[1]Zhu Y J,Liu Z F,Zhang W D.Entropy of nonautonomous dynamical systems[J].J.Korean Math.Soc.,2012,49:165-185.
[2]Jose S,?anovas.On entropy of non-autonomous discrete systems partic[J].Japnts of International Conference Dynamical Systems,2013:143-159.
[3]Christoph Kawan.Metric entropy of nonautonomous dynamical systems[J].arXiv:1304.5682v2[math.DS] 16 Jul.2013.
[4]Walters P.An Introduction to Ergodic Theory[M].New York:Springer Verlag,1982.
[5]孫文祥.遍歷論[M].北京:北京大學出版社,2012.
[6]Kolyada S,Snoha L.Topological entropy of nonautonomous dynamical systems[J].Random Comput.Dyn.,1996,4:205-233.
[7]Huang X J,Wen X,Zeng F P.Topological pressure of nonautonomous dynamical systems[J].Nonlinear Dynamics and Systems Theory,2008,8(1):43-48.
Remarks on variational principle of topological pressure of nonautonomous dynamical systems
Yang Jiang,Guo Yaxiao
(College of Mathematics,Northwest University,Xi′an710127,China)
This article uses the method similar to variational principle of nonautonomous entropy,proves variational principle of nonautonomous topological pressure about an inequality,introduces the principle of variational principle of nonautonomous entropy,and enriches the content of variational principle.
entropy of onautonomous,topological pressure of nonautonomous,variational principle
O189
A
1008-5513(2015)01-0036-07
10.3969/j.issn.1008-5513.2015.01.005
2014-10-10.
國家自然科學基金(11301417,11371292).
楊將(1987-),碩士生,研究方向:拓撲動力系統與遍歷論.
2010 MSC:22A30

