一類耦合Benjamin-Bona-Mahony型方程組的新精確解

趙燁，徐茜

(1.北京石油化工學(xué)院數(shù)理系，北京 102617；2.北京聯(lián)合大學(xué)基礎(chǔ)部，北京 100101)

一類耦合Benjamin-Bona-Mahony型方程組的新精確解

趙燁1，徐茜2

(1.北京石油化工學(xué)院數(shù)理系，北京 102617；2.北京聯(lián)合大學(xué)基礎(chǔ)部，北京 100101)

主要研究一類耦合的Benjamin-Bona-Mahony型方程組的顯式行波解.應(yīng)用展開法，Jacobi橢圓函數(shù)展開法以及詳細的計算，得到了方程組的多個精確行波解.所得結(jié)果推廣了方程組的sech ξ型孤立波解的存在性結(jié)果.

行波解；Benjamin-Bona-Mahony型方程組；展開法；Jacobi橢圓函數(shù)展開法

1　引言

眾所周知，數(shù)學(xué)物理以及工程中的許多現(xiàn)象可以用非線性發(fā)展方程來描述.這些方程的解的存在性以及解的形式有助于更好的解釋數(shù)學(xué)物理以及工程中的現(xiàn)象.所以尋找非線性發(fā)展方程的精確解是一個重要而又有趣的熱點問題.對此已經(jīng)提出了許多重要的方法，并得到了豐富的研究結(jié)果[1-8].

本文主要研究如下非線性發(fā)展方程組的顯式行波解：

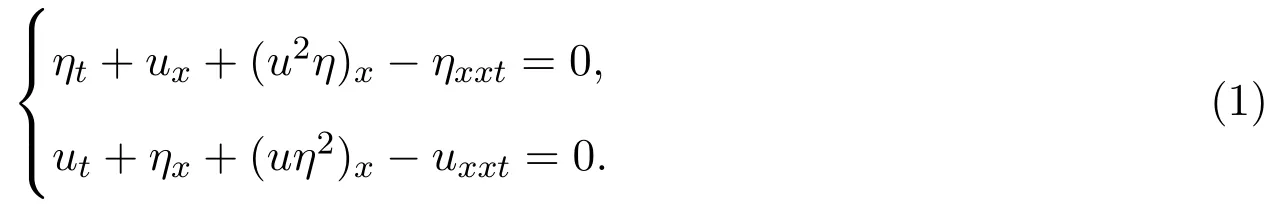
這個方程為文獻 [9]中 p=1的情形，它描述了水面上的小振幅長波.文獻 [9]得到了 (1) 的sech ξ型的孤立波解，其中ξ=x?ct，c代表波速.

2　雙曲函數(shù)、三角函數(shù)和有理函數(shù)解

對(1)式引入行波變換η(x，t)=φc(ξ)，u(x，t)=ψc(ξ)，得到

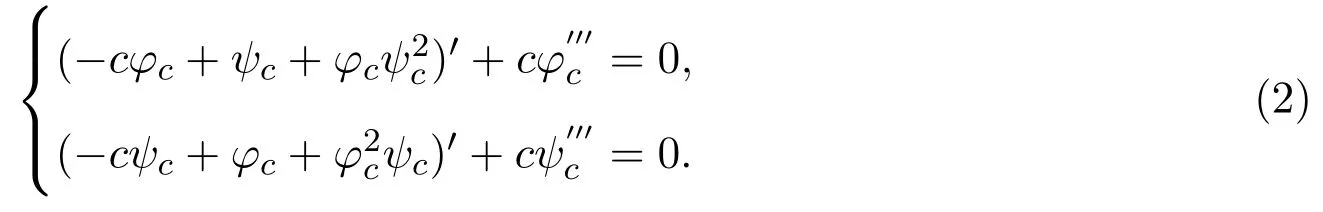
將(2)式積分一次，積分常數(shù)分別記為C1，C2，得到

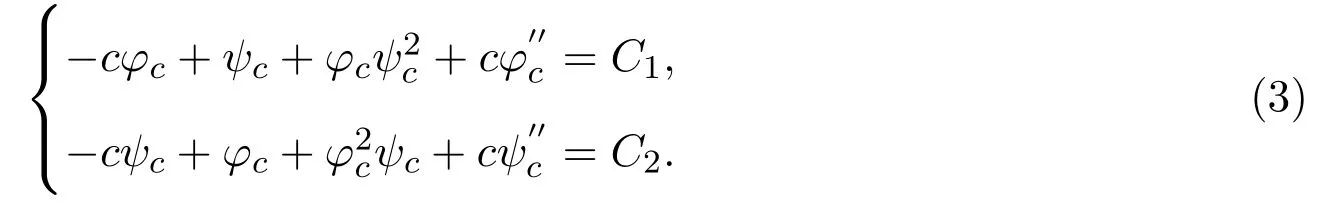
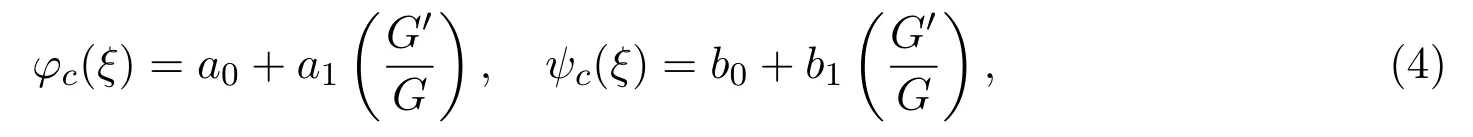
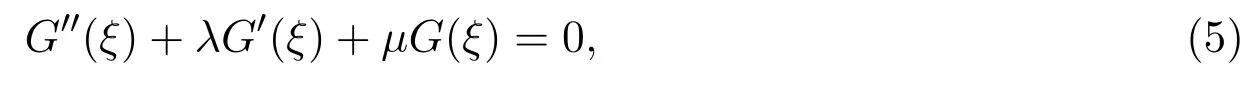
λ和μ是實常數(shù).利用(5)式的通解形式，得

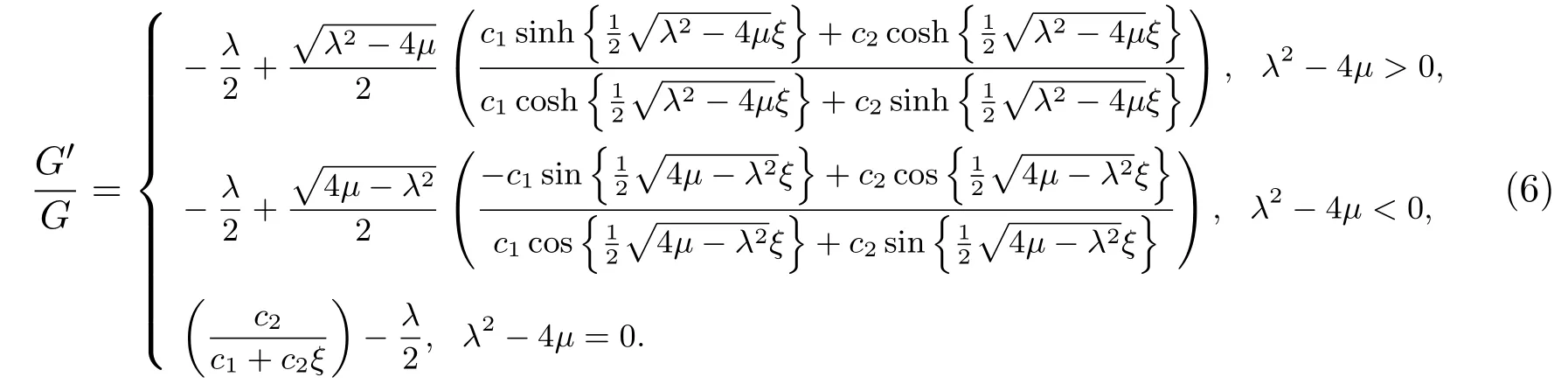
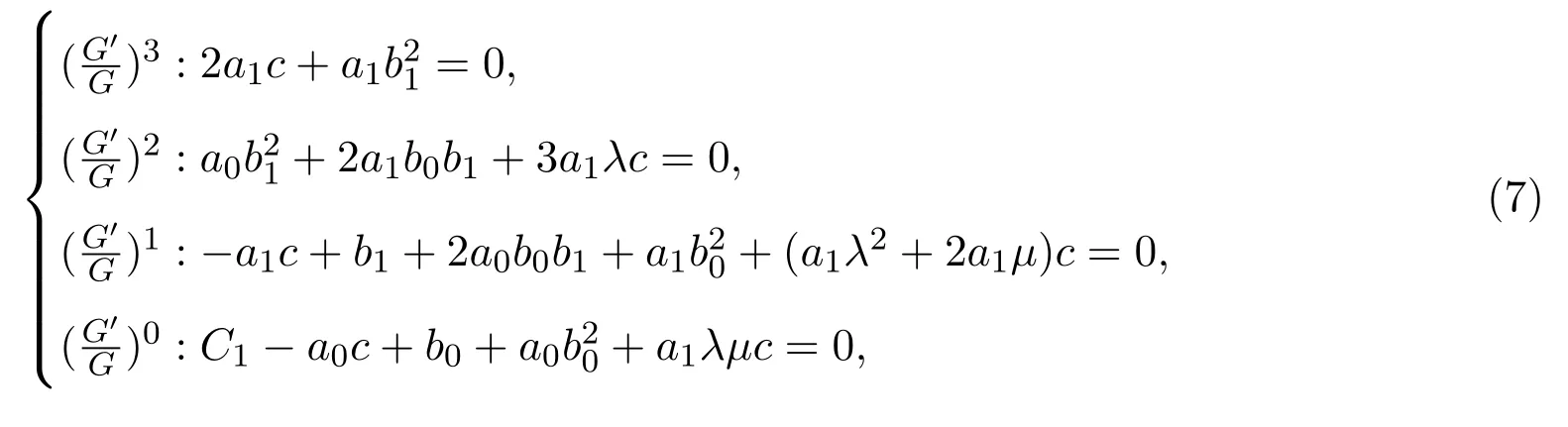
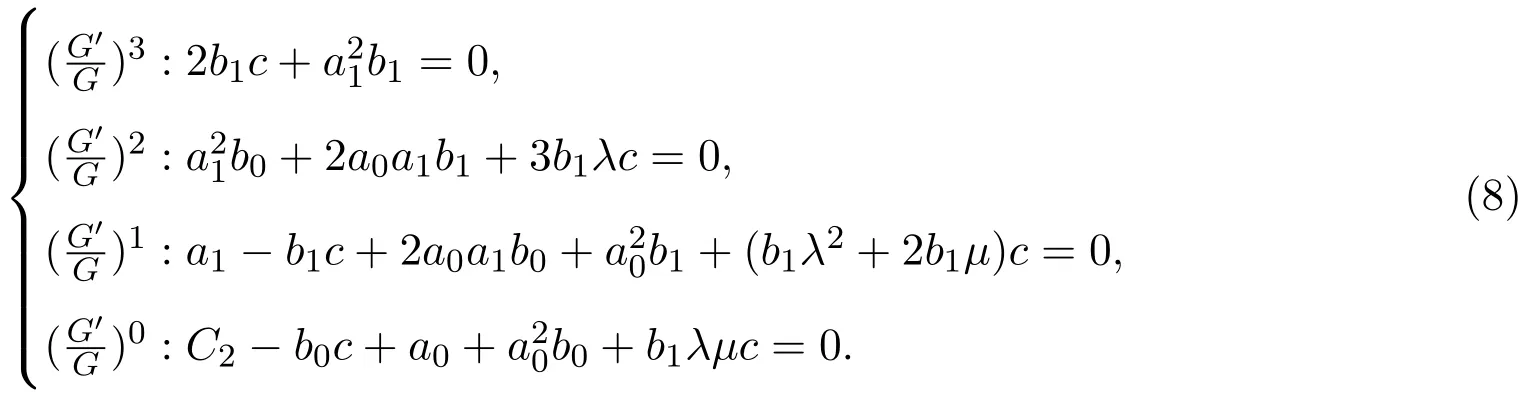
求解以上代數(shù)方程組，得到未知變量的兩組值：

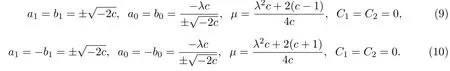
其中，c和λ為任意常數(shù).

將(9)式和(10)式分別代入(4)式，得到方程組(3)兩組解的表達式：

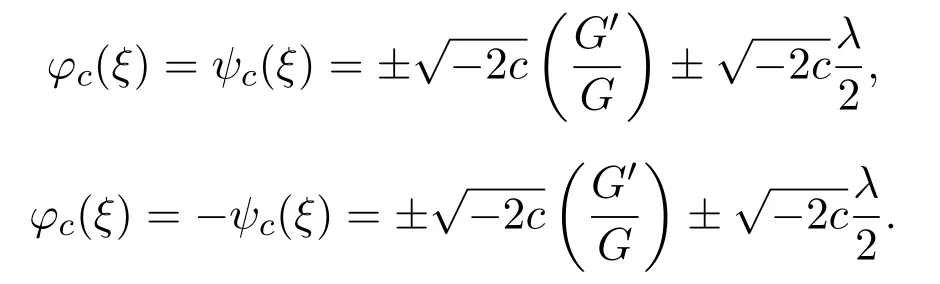
進一步，利用方程(5)的通解表達式(6)，得到方程組(1)的三種函數(shù)形式解.

a.當λ2?4μ＞0，即?1＜c＜0時，(1)式有雙曲函數(shù)形式解：

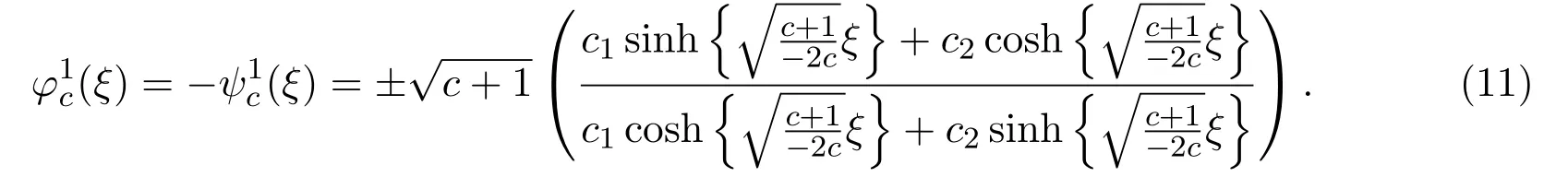
b.當λ2?4μ＜0，即c＜0或c＜?1時，(1)式有三角函數(shù)形式解：

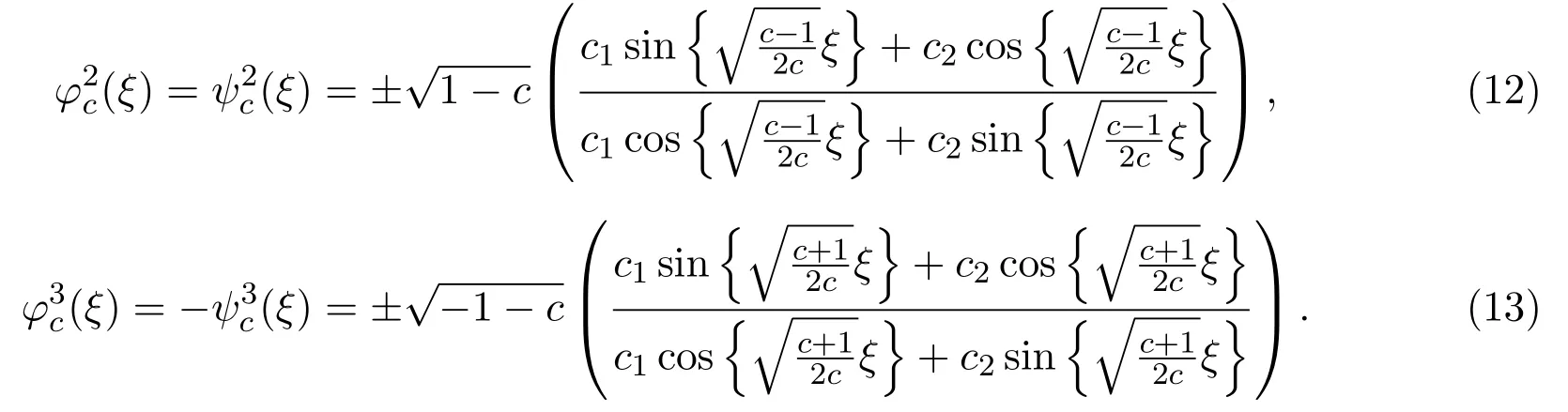
c.當λ2?4μ=0，即c=?1時，(1)式有有理函數(shù)形式解：

注 2.1如果c1?=0，c2=0，(11)式即為：

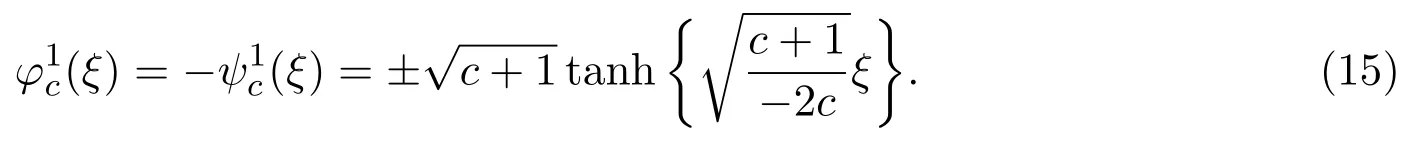
3　Jacobi橢圓函數(shù)解

本節(jié)求解方程組(2)的Jacobi橢圓函數(shù)形式解.考慮在(2)式中最高階導(dǎo)數(shù)項和非線性項的齊次平衡，設(shè)方程組(2)具有如下形式的解，其中cn為cnoidal函數(shù)，dn為dnoidal函數(shù)，

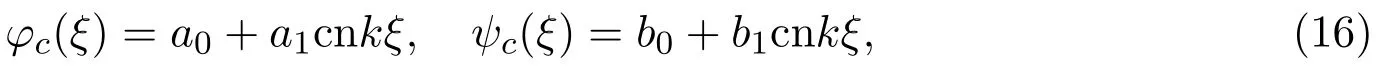
其中a1，a0，b1，b0，k為待定常數(shù).

將(16)式代入(2)式，得到關(guān)于待定常數(shù)的代數(shù)方程組：

其中m(0＜m＜1)是模數(shù).求解(17)式和(18)式，得到未知量的兩組值：

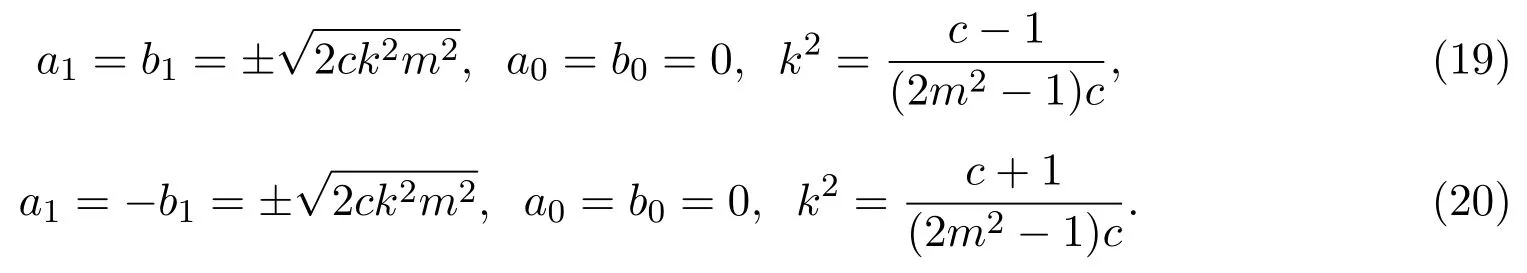
將(19)式和(20)式分別代入(16)式，得到方程組(1)的cnoidal函數(shù)形式解：

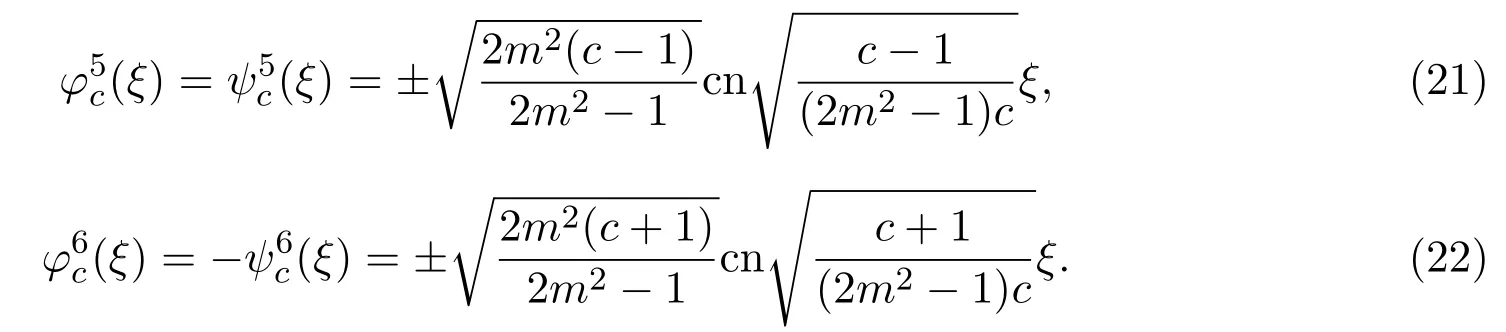
再次設(shè)方程組(2)具有如下形式的解：

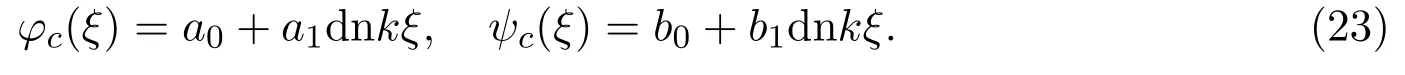
將(23)式代入(2)式，得到關(guān)于待定常數(shù)的代數(shù)方程組：

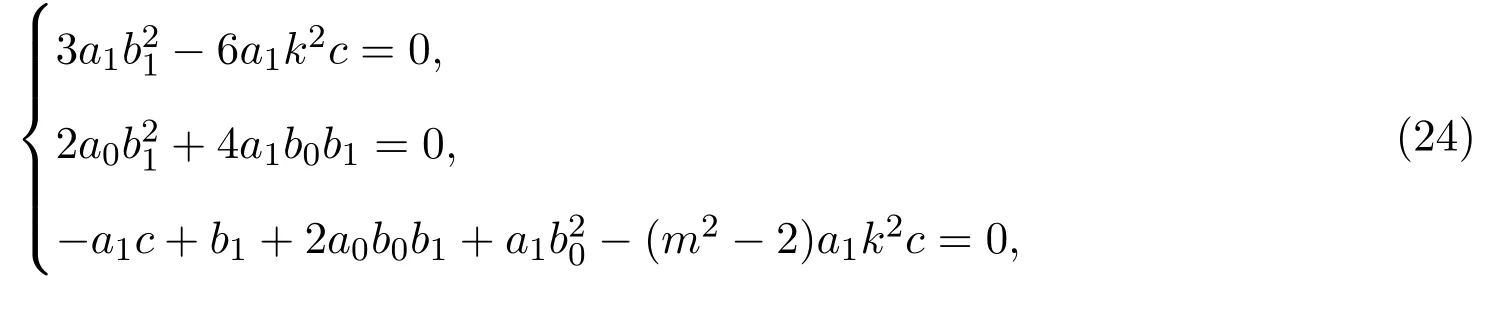
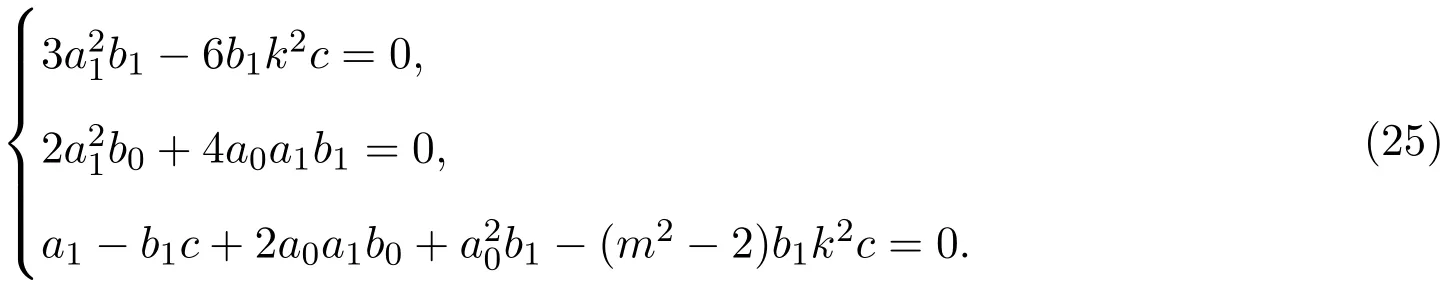
求解(24)式和(25)式，得到未知量的兩組值：

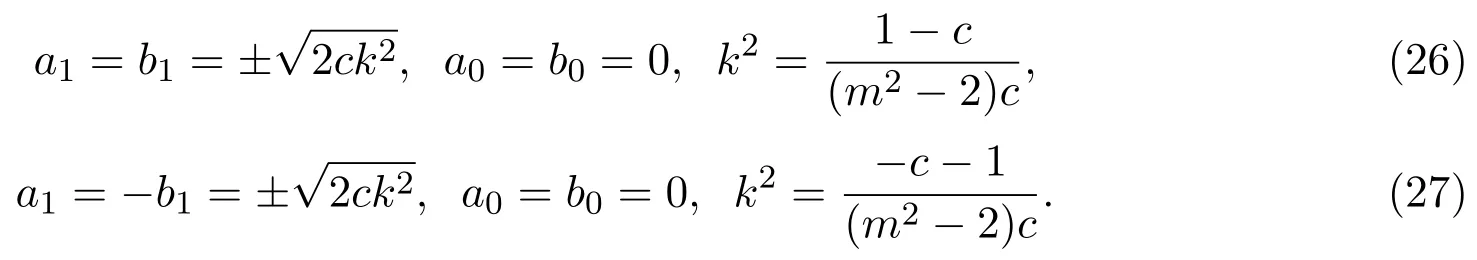
將(26)式和(27)式分別代入(23)式，得到方程組(1)的dnoidal函數(shù)形式解：

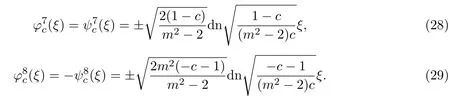
注3.1如果m=1，(21)(28)式和(22)(29)式即為文獻[9]中的孤立波解：

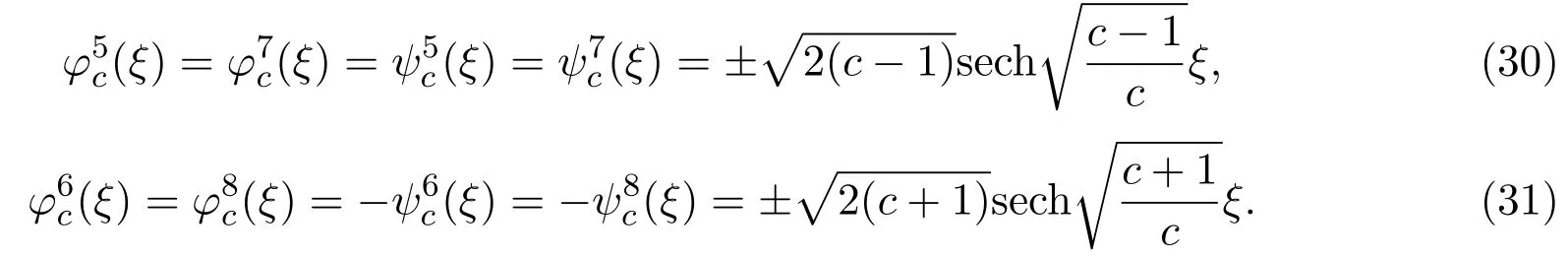
[1]Wang M，Li X，Zhang J.The-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J].Physics Letters A，2008，372：417-423.

[2]Ali Akbar M，Norhashidah Hj Mohd Ali，Zayed E M E.A generalized and improved-expansion method for nonlinear evolution equations[J].Mathematical Problems in Engineering，2012，Article ID 459879，22 pages.

[3]Taha W M，Noorani M S M，Hashim I.New exact solutions of sixth-order thin-film equation[J].Journal of King Saud University-Science，2014，26：75-78.

[4]Liu Shikuo，F(xiàn)u Zuntao，Liu Shida，et al.Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J].Physics Letters A，2001，289：69-74.

[5]Fu Zuntao，Liu Shikuo，Liu Shida，et al.New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations[J].Physics Letters A，2001，290：72-76.

[6]Huang Wenhua，Liu Yulu，Lu Zhiming，et al.The extended Jacobi elliptic function expansion method and its applications in weakly nonlinear wave equations[J].Journal of Hydrodynamics Ser.B，2006，18(3)：352-361.

[7]王倩，陳曉燕.擴展的Sinh-Gordon方程展開法與Kaup-Kupershmidt方程的Jacobi橢圓函數(shù)解[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué)，2013，29(2)：159-163.

[8]曹瑞.帶色散項的高階非線性Schr?dinger方程的精確解[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué)，2012，28(1)：92-98.

[9]Cui Liwei.Existence，orbital stability and instability of solitary waves for coupled BBM equaions[J].Acta Mathematicae Applicatae Sinica，English Series，2009，25：1-10.

New explicit solutions for some coupled Benjamin-Bona-Mahony type equations

Zhao Ye1，Xu Qian2
(1.Department of Mathematics and Physics，Beijing Institute of Petrochemical Technology，Beijing102617，China；
2.Department of Basic Courses，Beijing union university，Beijing100101，China)

This paper mainly investigates explicit traveling wave solutions for some coupled Benjamin-Bona-Mahony type equations.Applying the-expansion method and Jacobi elliptic function method，and by detailed computation，many traveling wave solutions are obtained.The results extend the existence result of sech ξ type solitary wave solutions for the equations.

traveling waves，Benjamin-Bona-Mahony equaiton，-expansion method， Jacobi elliptic function expansion method

O175.2

A

1008-5513(2015)01-0012-06

10.3969/j.issn.1008-5513.2015.01.002

2014-03-05.

北京市教委科技計劃項目(KM201210017008，KZ201310028030)；北京石油化工學(xué)院青年基金(N1004).

趙燁(1978-)，博士，講師，研究方向：偏微分方程.

2010 MSC:35Q58