在動手操作中經歷“數學化”

郭由湘

“平行四邊形的面積"是在學生掌握了長方形面積的計算和認識了平行四邊形的基本特性的基礎上的教學內容。在我區小學數學“同課異構”展示活動中，彭小紅老師展示的“平行四邊形的面積”課堂教學非常精彩，讓學生在動手操作中經歷“數學化”的過程。下面摘取其中幾個精彩片段與同仁們分享。

【片段一】創設情境，激發“探”欲

師（導入）：在動物村里住著兩只小兔，一只小白兔，一只小黑兔。小白兔住在村東頭，它的菜地卻在村西頭；小黑兔住在村西頭，它的菜地卻在村東頭，它們都覺得很不方便。于是它們商量把地換一下。可是小白兔的菜地是長方形的，小黑兔的菜地是平行四邊形的，同學們，你們說這樣交換公平嗎？誰能幫幫它們嗎？

生1：只要算出這兩塊地的面積，比比就知道了。

師：我們已經學過哪些圖形的面積計算公式？

生2：學了長方形的面積計算公式，長方形的面積=長×高。

師：那么怎么求出平行四邊形的面積呢？這就是我們今天要探究的問題。

……

【賞析】彭老師用學生喜歡的小故事導入，讓學生產生想幫助小兔的強烈愿望，進而激發他們希望盡快找到平行四邊形面積的計算方法，這樣就充分調動了學生主動探索的積極性，為下面的探究活動做好了鋪墊。

【片段二】借助實驗，積極探究

師：請大家嘗試算算下列平行四邊形（底為6，鄰邊為5，高為4）的面積，并說明算法。

（學生分組活動：計算，討論，交流結果，教師巡視。）

生1：我算得平行四邊形面積為6×5=30。（鄰邊×鄰邊）

生2：我的算法是：底×高=6×4=24。

師： 好。出現了兩種不同的算法，到底哪種算法合理呢？下面大家一起來探究平行四邊形的面積和誰有關系？（拿出學具）

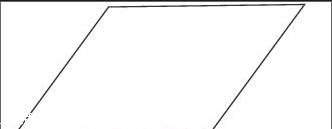
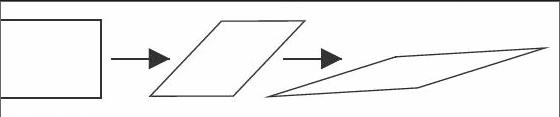
學生活動：拉一個長方形框架，慢慢變成平行四邊形， 最后拉平。

師：在慢慢拉的過程中，周長變了嗎？

生3：周長沒有變。

師：圖形的面積變了嗎？

生4：面積變了。

師：面積是怎么變化的？

生5：面積逐漸變小，最后會變成0。

生6：這也證明了剛才同學的算法（鄰邊×鄰邊）是錯誤的。因為拉動框架時，四條邊都沒有變化，但面積卻變小了。

師：那為什么面積變小了？

生7：平行四邊形的高在逐漸變小。

師：這個實驗說明平行四邊形面積與高有關。

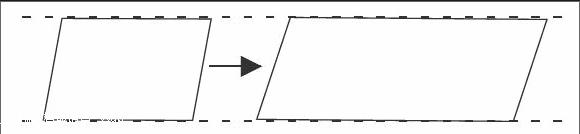
投影（動畫）：平行四邊形的一組對邊逐漸延長，高不變。

師：大家看到什么變了？什么沒變？

生8：平行四邊形變“長”了。

生9：平行四邊形的底變長了，周長變長了。

師：很好，那它的面積有沒有變化？

生10：面積逐漸增大。

師：是什么原因使面積變大的？

生11：由于底變長使平行四邊形的面積變大。

師：你真棒！說明平行四邊形的面積與它的底有關。綜合以上探究，說明平行四邊形的面積與它的底和高有關。

【賞析】首先讓學生嘗試求平行四邊形的面積，由此產生兩種結果，引發學生思維沖突。接著，通過拉伸平行四邊形框，讓學生進一步感悟平行四邊形的特性，從而自主發現平行四邊形的面積與它的底和高有關，這樣既訓練了學生的思維能力，又培養了學生的合情推理能力。

【片段三】觀察比較，引發猜想

師：在學習推導長方形的面積公式時，我們最初使用了數方格的方法。今天學習計算平行四邊形的面積，能不能也用這個方法？

學生活動：請仔細觀察課本中方格紙上的兩個圖形，數一數，把表格填完整。（1小格代表1平方米，不滿1格的都按半格計算。）

生1：長方形的面積是24平方米。

師：請說說長方形的面積是怎樣數出來的？

生2：先橫著數有6格，再豎著數有4格，6×4=24格，是24平方米。

師：平行四邊形的面積你們是怎樣數出的？

生3：先數有20個整格是20平方米；再數有8個半格，把每2個半格合成一個整格是4平方米，共有24平方米。

生4：先數一行，整格的有5個。然后再把左邊不滿一格的移到右邊的不滿一格剛好拼成一個整格，每行都有6個整格。共有4行，6×4=24個整格，也就是24平方米。

如圖所示：

師：你真聰明！想法很獨特，有創意，把不完整的格拼成完整的格，體現了“割補”的數學思想方法。大家鼓勵鼓勵他！

師：同桌交流一下填法，誰愿意匯報一下你的成果？

生5：平行四邊形的底是6米，高是4米，面積是24平方米；長方形的長是6米，寬是4米，面積是24平方米。

師：觀察表格你發現了什么？

生6：我發現平行四邊形的底和長方形的長相等，平行四邊形的高和長方形的寬相等，平行四邊形的面積和長方形的面積也相等。

【賞析】用數方格的方法得到圖形的面積，是學生熟悉的、直觀計量面積的方法。同時呈現平行四邊形和長方形兩個圖形，暗示了它們之間存在某種聯系，由數據上的相關性引發出學生大膽的猜想：“平行四邊形的面積也應該等于底×高。”更加精彩處在于：有學生在數方格時指出，每兩個半格可以拼成一個整格，即每一行左邊的半格“移到”和最右邊的半格可以拼成一個整格。這就是“割補”法的原型，為下一步剪拼圖形提供理論依據和思考方法。

【片段四】動手剪拼，感悟“轉化”

師：看來，數方格的方法可以得到這個平行四邊形的面積，現在我想得到一個很大的平行四邊形花壇的面積，你認為數方格的方法怎么樣？

生1：不合適。

師：那能不能找到一種方法，適用于計算所有平行四邊形的面積呢？

課件演示：我們把等底等高的平行四邊形和長方形兩個圖形平移、重疊，你們發現了什么？

生2：兩個圖形不能完全重合，當底完全重合時，剛好相差一個直角三角形。

生3：設想把多出的三角形剪下來向左平移，如果能剛好拼接成長方形，那么原來的平行四邊形和長方形的面積一樣大。

生4：由此得到啟示，我們可以把右邊的三角形剪下來，移到左邊就拼成一個長方形。這樣，平行四邊形就變成了長方形。

師：對，平行四邊形轉化成長方形，新知識變成舊知識，多么好的方法呀！這里用到了“轉化”的數學思想。

生5：剪歪了怎么辦？

師：問得好！誰來幫助？

生6：可以先用尺子畫一條高，再去剪。

（學生活動：用準備好的學具（平行四邊形紙板、剪刀），分小組合作剪一剪、拼一拼圖形，教師巡視，各組代表上臺匯報展示。）

組1：我們組把平行四邊形沿高剪下一個直角三角形，向右平移，能拼成一個長方形。（學生把拼接后的長方形與原來的平行四邊形一上一下貼在黑板上，使長方形的長與平行四邊形的底一樣長。）

組2：我們組把平行四邊形沿高剪下一個直角梯形，向左平移，也能拼成一個長方形。（學生把拼接后的長方形與原來同樣的平行四邊形紙板，一左一右貼在黑板上，使長方形的寬就是平行四邊形的高。）

（板書：沿高剪—平移—拼接）

師：其他同學還有什么補充嗎？

生7：只要沿著任意一條高剪下，都可以拼成一個長方形，這樣平行四邊形就轉化成了長方形。

師：同學們，剛才我們把不會求的平行四邊形的面積，通過剪拼，變成了會求的長方形的面積，其實這種方法是數學上的一種重要的思想方法——轉化。轉化就是把不會求的轉化成會求的，把未知的轉化成已知的。

師：為什么要沿著高剪呢？

生8：這樣沿著高剪，才能把平行四邊形拼成一個長方形。

師：很好！可我有點不明白，把它拼成了長方形，這個長方形的面積還是原來平行四邊形的面積嗎？

……

【賞析】教師讓學生在畫、剪、拼等一系列實驗活動中理解和掌握平行四邊形和轉化后的長方形之間的聯系， 通過合作、觀察、思考、交流等活動驗證了“平行四邊形面積=底×高”的正確性。在探索活動中，留給學生充分探索、交流的空間，使學生學會與他人合作，同時也使學生學到了怎樣由已知探索未知的思維方式與方法，培養他們主動探索的精神，讓學生在活動中學習，在活動中發展。

總之，本課的教學主線非常清晰，內容豐富，構思巧妙。教學過程由淺入深，由具體到抽象，由感性到理性。引導學生通過數方格、拉方框、剪拼圖等形式，步步深入，緊扣主題，讓學生親身經歷數學知識的“再發現”“再創造”過程，引起學生濃厚的學習興趣，促使他們積極主動地參與探究知識形成過程。學生在觀察中理解，在操作中感知，溝通了知識的內涵，領悟了學習方法，轉變學習方式，極大地提高了教學效益。

教學中，教師讓學生“做中學”，經歷“數學化”的過程，使學生“學會思考”，感悟“數學思想”。讓學生學會數學地思考，是數學課程的重要目標之一。教師借助數方格的方法，學生由長方形面積公式猜想平行四邊形的面積計算公式；在數平行四邊形的面積時發現同一行的兩個半格可以“剪拼”成一個整格，學生學會了“割補” 方法，通過“剪拼”，平行四邊形轉化成了長方形，學生感悟了“轉化”的數學思想。這些教學活動的安排，不僅吸引學生充分參與數學學習過程，自覺調動已有的知識經驗和心智技能，從而促使數學學習活動有效地展開并不斷深入，更重要的是讓學生學會數學思考，學會用數學方法解決現實中的問題。（作者單位：江西省吉安市青原區教研室）

責任編輯 周瑜芽

E-mail：jxjyjzyy@163.com